高速铁路大跨度钢桁架桥接触网腕臂安装技术研究

卢广苗

(中铁第四勘察设计院集团有限公司,武汉 430063)

1 概述

近年来,随着我国高速铁路的快速发展,跨江、跨海等大跨度钢桁架桥不断涌现[1],如郑武高铁武汉天兴洲长江大桥钢桁梁跨度1 092 m,最大设计伸缩量为±500 mm[2];深江铁路广中江特大桥钢桁架桥梁体主跨1 412 m,最大设计伸缩量为±650 mm;巢马铁路长江公铁两用大桥钢梁梁端最大设计伸缩量为±850 mm;沪苏通铁路沪苏通长江公铁大桥钢桁架梁跨度1 092 m,最大设计伸缩量达±900 mm[3]。

大跨度钢桁架梁引起的梁体伸缩对接触网腕臂安装、偏移调整等系统设计带来诸多不利影响。腕臂偏移过大会使接触网拉出值[4]、导高等系统参数发生较大变化[5],引起定位器、吊弦处产生硬点、燃弧率超标等降低接触网弹性指标及弓网受流质量[6]等问题,严重时可导致定位线夹拉脱、打弓等故障[7],对于双支腕臂会产生物理冲突或绝缘距离不足等问题;腕臂偏移不均表现为腕臂向其中一侧偏移过大,同样会引起上述问题,均不利于高速铁路的运行安全[8]。在大跨度桥梁区段,若不考虑桥梁伸缩对接触网腕臂安装的影响,上述问题将进一步加剧。

为保证高速铁路接触网的安全运行,本次对高速铁路大跨度钢梁区段接触网腕臂安装做深入技术研究。

2 大跨度钢梁伸缩对接触网腕臂安装的影响分析

2.1 腕臂偏转工作原理

腕臂是用于固定接触网承力索和接触线的支撑结构装置[9]。常规设计中腕臂受导线伸缩影响随温度变化发生线性偏转[10],具体体现为温度升高→导线伸长→腕臂向下锚侧偏移,温度降低→导线缩短→腕臂向中锚侧偏移[11]。锚段关节双腕臂底座最小间距由两支腕臂最大偏转量直接决定[12],高速铁路双腕臂底座最小间距如图1所示。

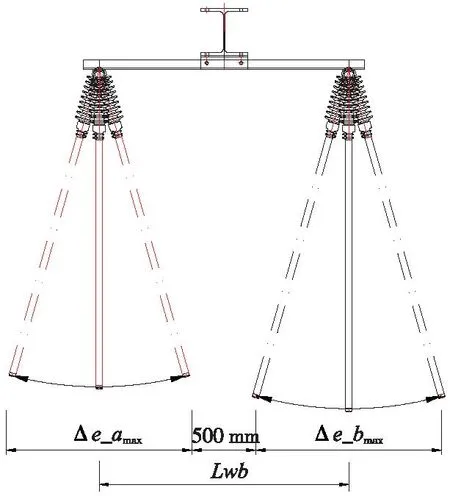
图1 高速铁路双腕臂底座最小间距示意Fig.1 Schematic diagram of minimum spacing between double cantilever bases of high-speed railways

高速铁路接触网双腕臂间距最小距离一般按≮450 mm控制[13],考虑腕臂露头等因素影响一般按500 mm进行设计[14]。高速铁路双腕臂底座的最小间距Lwb可按以下公式计算确定

Lwb=(Δe_amax+Δe_bmax)/2+0.5

(1)

式中,Δe_amax,Δe_bmax分别为两支腕臂的最大腕臂偏移量。

2.2 钢梁纵向伸缩对腕臂安装的影响分析

桥梁伸缩会引起接触网支柱产生位移,导致接触网腕臂与中锚柱之间的距离发生改变,进而影响腕臂偏移;混凝土桥梁及小跨度钢梁伸缩量小,对接触网腕臂偏移的影响很小;大跨度钢梁伸缩位移大,在不利情况下引起的腕臂偏移量可达±(0.5～1.0) m,是影响锚段关节双支腕臂间距取值的关键因素,也是引起拉出值等接触网系统参数产生变化的重要因素。

高速铁路接触网系统能否正常工作直接影响高速列车的安全运行,在大跨度钢桁架桥区段不可忽视钢梁纵向伸缩对接触网腕臂安装、偏移调整等系统设计的影响。

2.3 钢桁架桥纵向伸缩机理

桥梁伸缩对腕臂偏移的影响较为复杂[15],为便于下文相关研究、计算,需简要说明钢桁架桥纵向伸缩机理。

钢桁架桥主要受温度、制动力、风荷载及活载等影响产生纵向位移伸缩[16],伸缩量的大小与梁体结构形式、钢梁整体跨度、环境温度等多种因素有关[17]。

(1)环境温度变化一般是大跨度钢桁架桥产生纵向伸缩的主要因素,温度作用下引起的梁桥伸缩包括线性温度变化和梯度温度变化。线性温度变化引起的梁体变形产生的纵向伸缩量大;梯度温度变化对桥梁结构的影响主要为应力变化,应力变化引起纵向伸缩量相对较小,在计算桥梁伸缩量时一般在安全系数中统一考虑。温度变化引起的梁体最大伸缩量qtmax位于梁端,其余梁上各个点位的最大纵向伸缩量qt_ρmax以温度伸缩零点为中心进行内插计算[18]得出,具体如下。

梁体任意一点最大伸缩量

qt_ρmax=qtmax×Lρ/Lq

(2)

梁端实时伸缩量

qt=β×(tq-tqmin)×Lq

(3)

梁体任意一点实时伸缩量

qt_ρ=β×(tq-tqmin)×Lρ

(4)

式(3)、式(4)中,β为桥梁梁体线温度膨胀系数(1/℃),由桥梁专业提供或按桥梁专业提供的设计参数计算得出。

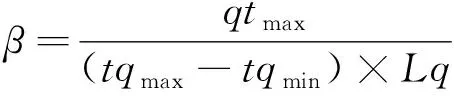
(5)

式中,tqmax为梁体最高计算温度;tqmin为梁体最低计算温度;tq为梁体现场实时温度;Lq为梁端与钢梁温度伸缩零点的距离;Lρ为梁体任意一点与钢梁温度伸缩零点的距离。以桥梁在tqmin温度时,梁体伸长量等于0为基准进行相关公式推算,如钢桁架桥梁端受温度影响伸缩变化范围为±0.3 m,则qtmax=0.6 m。

(2)制动力及纵向风荷载引起的纵向位移相对较小,在其作用下引起钢梁整体产生位移,即钢梁任意位置产生的纵向位移量均与梁端一致[19]。在活载作用下,钢梁梁体不同位置产生的伸缩量不同且变位复杂,其最大变形量一般位于梁端,鉴于活载对钢梁伸缩影响较小,下文相关研究采取极限状态法按钢梁任意位置受活载影响产生的位移量均与梁端一致进行计算。以qεmax表示活载、制动力及风荷载引起的梁体最大综合位移量。

(3)qtmax、qεmax、tqmax、tqmin等数值由桥梁专业计算并提供,本文不再赘述。

2.4 钢梁伸缩在不同工况锚段布置方式下引起的腕臂偏移分析

大跨度钢梁区段接触网锚段关节及中锚布置位置不同,钢梁伸缩引起的接触网腕臂偏移方向和偏移量不同,与导线伸缩因素引起的腕臂偏移存在叠加和相减两种关系。基于尽可能减小坠砣行程范围,文章《高速铁路大跨度钢桁架桥接触网关键技术研究》已完成接触网在不同跨度钢桁架桥的最优锚段布置方式[20],总结如下。

(1)跨度720 m以下的钢梁。建议将中心锚结布置在钢梁温度伸缩零值处,两侧锚段关节布置在靠近伸缩缝的混凝土梁上。

(2)跨度720～849 m的钢梁。建议将锚段关节布置在钢梁温度伸缩零值处,两侧中心锚结布置在靠近伸缩缝的混凝土梁上。

(3)跨度大于850 m的钢梁。建议伸缩缝处半锚长度尽量做短,其中关节布置在靠近伸缩缝的钢梁梁上,中心锚结布置在靠近伸缩缝的混凝土梁上;整体布置在钢梁本体上的接触网建议适当缩短锚段长度。

(4)不得跨伸缩缝设置锚段关节;为保证高速铁路接触网状态参数,大跨度钢桁架桥上不宜设置绝缘关节或电分相。

腕臂偏移量与坠砣行程变化量成正比关系,上述推荐锚段布置方式能有效降低钢梁伸缩对坠砣行程的影响,同样也可降低钢梁伸缩对腕臂偏移的影响。在上述成果基础上进一步细化研究导线伸缩及钢梁伸缩对不同工况接触网腕臂偏移的影响和相互关系,见图2和表1。

表1 温度作用下钢梁伸缩与导线伸缩对腕臂偏移影响相互关系对比Tab.1 Comparison of the influences of steel beam expansion and conductor expansion on cantilever deflection under the influence of temperature

图2 不同跨度钢梁区段接触网推荐锚段布置方式Fig.2 Optimal anchor section layout of catenary in steel beam sections with different spans

当腕臂柱与中心锚结同时位于钢桁架桥上时,钢桁架桥上的腕臂偏移不受因活载、制动力及风荷载引起的qεmax桥梁伸缩影响。

根据本节研究,当桥梁伸缩对腕臂偏移有影响时,桥梁伸缩引起的腕臂偏移与导线伸缩引起的腕臂偏移有叠加关系和相减关系两种情况。

3 大跨度钢梁伸缩影响下腕臂偏移计算

3.1 腕臂最大偏移量计算

腕臂最大偏移量主要由腕臂处导线受温度变化引起的最大导线伸缩量及钢梁伸缩引起的最大腕臂偏移量两个因素共同决定。

3.1.1 腕臂柱不受桥梁伸缩影响

腕臂最大偏移量[21]

Δemax=α×ΔTx×Lw

(6)

式中,ΔTx为接触悬挂导线最大计算温差,ΔTx=txmax-txmin,其中txmax接触悬挂导线最高计算温度;txmin为接触悬挂导线最低计算温度;Lw为腕臂柱与中心锚结的距离。

3.1.2 腕臂柱与中心锚结同时位于钢桁架桥上

①叠加关系时腕臂最大偏移量为

Δemax=α×ΔTx×Lw+ΔLwmax

(7)

②相减关系时腕臂最大偏移量为

Δemax=max(α×ΔTx×Lw,ΔLwmax)

(8)

式中,α为铜合金导线的线温度膨胀系数(1/℃)。

式(7)、式(8)中ΔLwmax为温度作用下桥梁伸缩引起的最大腕臂偏移量(即温度作用下腕臂柱与中心锚结距离受桥梁伸缩影响产生的最大变化量),此值由腕臂柱与中心锚结的距离Lw决定,具体为

ΔLwmax=qtmax×Lw/Lq

(9)

3.1.3 腕臂柱与中心锚结不同时位于钢桁架桥上

①叠加关系时腕臂最大偏移量为

Δemax=α×ΔTx×Lw+qεmax+ΔLsmax

(10)

②相减关系时腕臂最大偏移量为

Δemax=max(α×ΔTx×Lw+qεmax,ΔLsmax+qεmax)

(11)

式(10)、式(11)中ΔLsmax为温度作用下桥梁伸缩引起的最大腕臂偏移量(即温度作用下腕臂柱至钢梁温度伸缩零点距离受桥梁伸缩影响产生的最大变化量),此值由腕臂柱与钢梁温度伸缩零点的距离Ls决定

ΔLsmax=qtmax×Ls/Lq

(12)

3.2 腕臂安装曲线计算

准确的腕臂安装曲线能有效避免腕臂向两侧偏移不均引起的弓网问题[22]。在大跨度钢梁区段,腕臂偏移受导线伸缩和钢梁伸缩共同影响,因此,腕臂安装曲线(腕臂实时偏移量Δe)需结合钢梁伸缩因素对常规设计计算公式进行修正。

常规设计中腕臂偏移仅受导线伸缩因素影响时,腕臂无偏转时的安装温度为tx0=(txmax+txmin)/2;在仅受桥梁伸缩影响下,腕臂无偏转时的安装温度为tq0=(tqmax+tqmin)/2。

制动力、风荷载及活载引起桥梁伸缩导致的腕臂偏移一般在列车通过钢桁架桥时产生,计算腕臂最大偏移量时应予以考虑,但由于腕臂安装及调整时不会有高速列车通行,故腕臂安装曲线计算公式中可不体现qεmax的影响。

3.2.1 腕臂柱不受桥梁伸缩影响[17]

Δe=α×(tx-tx0)×Lw

(13)

式中,tx为接触导线现场实时温度(下同)。

3.2.2 腕臂柱与中心锚结同时位于钢桁架桥上

①叠加关系时

Δe=α×(tx-tx0)×Lw+ΔLw

(14)

②相减关系时

Δe=α×(tx-tx0)×Lw-ΔLw

(15)

式(14)、式(15)中,ΔLw为在温度作用下腕臂柱至中心锚结距离受桥梁伸缩影响产生的实时变化量:ΔLw=β×Lw×(tq-tq0)。

3.2.3 腕臂柱与中心锚结不同时位于钢桁架桥上

①叠加关系时

Δe=α×(tx-tx0)×Lw+ΔLs

(16)

②相减关系时

Δe=α×(tx-tx0)×Lw-ΔLs

(17)

式(16)、式(17)中,ΔLs为在温度作用下腕臂柱至钢梁温度伸缩零点距离受桥梁伸缩影响产生的实时变化量:ΔLs=β×Ls×(tq-tq0)。

腕臂实时偏移量Δe为正时代表腕臂向下锚侧偏转,Δe为负时代表腕臂向中锚侧偏转;腕臂偏移安装曲线受tx和tq两个变量共同影响,且tx与tq间无直接对应关系;钢桁架桥现场实际温度tq值随机变化且较为复杂[23],与钢梁所处地理位置、环境温度[24]、风速、日辐射强度、雨雾[25]等因素密切相关,在工程实际应用中需参考桥梁专业相关资料对钢桁架桥的实时温度值进行测定,本文不做深入探讨,建议tq值按近似等于现场环境气温,同时按tq=min(tq,tqmax)进行相关计算。

3.3 典型案例计算

3.3.1 工况2典型工点计算

设定第2.4节工况2中钢桁架桥总跨度为850 m,其中

Lw1=100 m(3号腕臂柱);

Lw2=575 m(10号腕臂A支);

Lw3=500 m(10号腕臂B支);

Ls1=400 m;Ls2=75 m;

Lq1=Lq2=425 m;

txmax=80 ℃;txmin=-20 ℃;

tqmax=35 ℃;tqmin=-35 ℃;

α=0.000 017(1/℃);

β=0.000 015(1/℃);

tx0=30 ℃;

qt_amax=0.446 m;qt_bmax=0.446 m;

qεmax=0.24 m。

按上述参数对3号柱、10号柱进行典型腕臂安装曲线及最大偏移量计算。

①3号柱腕臂偏移为叠加关系且腕臂柱与中锚不同时位于钢桁架桥上。

按式(16)、式(18)计算腕臂安装曲线

Δe=α×(tx-tx0)×Lw1+β×Ls1×(tq-tq0)=

0.001 7tx+0.006tq-0.051;

按式(10)、式(12)计算腕臂最大偏移量

Δemax=(α×ΔTx×Lw1)+qεmax+

(qt_amax×Ls1/Lq1)=0.85 m。

②10号柱双腕臂A支偏移为相减关系且腕臂柱与中锚不同时位于钢桁架桥上。

按式(17)、式(18)计算腕臂安装曲线

Δe=α×(tx-tx0)×Lw2-β×Ls2×(tq-tq0)=

0.009 8tx-0.001 1tq-0.293 3;

按式(11)、式(12)计算腕臂最大偏移量

Δemax=max((α×ΔTx×Lw2+qεmax),

(qt_bmax×Ls2/Lq2+qεmax))=

max(1.218,0.32)=1.218 m。

③10号柱双腕臂B支偏移为叠加关系且腕臂柱与中锚不同时位于钢桁架桥上。

按式(16)、式(18)计算腕臂安装曲线

Δe=α×(tx-tx0)×Lw3+β×Ls2×(tq-tq0)=

0.008 5tx+0.001 1tq-0.255;

按式(10)、式(12)计算腕臂最大偏移量

Δemax=(α×ΔTx×Lw3)+qεmax+

(qt_bmax×Ls2/Lq2)=1.169 m。

④10号柱双腕臂底座最小间距

Lwb=(1.218+1.169)/2+0.5=1.694 m。

上文提到tq值的测定较为复杂,且tx与tq间无直接对应关系,为便于本次研究成果的直观呈现,假定tq=min(tx,tqmax)进行计算,得出腕臂安装曲线如图3所示。

图3 工况2腕臂典型安装曲线Fig.3 Typical cantilever installation curve of condition 2

综上,针对跨度720～849 m的钢梁,采用工况2锚段布置方式时腕臂偏移量整体较小。

3.3.2 工况3典型工点计算

设定第2.4节工况3中钢桁架桥跨度为2 000 m,假定tq=min(tx,tqmax),在常规锚段布置方式下对3号柱、4号柱进行典型腕臂安装曲线计算如图4所示。

根据图4典型设计参数,工况3中3号柱、4号柱最大偏移量计算如下。

①3号柱腕臂偏移为叠加关系且腕臂柱与中锚不同时位于钢桁架桥上,腕臂最大偏移量按式(10)、式(12)计算: Δemax=2.054 m。

②4号柱双腕臂A支偏移为叠加关系且腕臂柱与中锚不同时位于钢桁架桥上,腕臂最大偏移量按式(10)、式(12)计算: Δemax=2.087 m。

③4号柱双腕臂B支偏移为相减关系且腕臂柱与中锚同时位于钢桁架桥上,腕臂最大偏移量按式(8)、式(9)计算:Δemax=max(1.28,1.237)=1.28 m。

④4号柱双腕臂底座最小间距

Lwb=(2.087+1.28)/2+0.5=2.184m。

综上,工况3中当钢梁伸缩与导线伸缩对腕臂偏移的影响为叠加关系时,钢梁伸缩对接触网系统设计非常不利。若将上述工况3典型案例中的Lw1调整为100 m、Lw2调整为150 m,经计算腕臂安装曲线如图5所示。

图5 缩短锚段长度布置时工况3腕臂典型安装曲线Fig.5 Typical cantilever installation curve of condition 3 by shorting the length of anchor section

根据图5典型设计参数,缩短锚段长度后,工况3中3号柱腕臂最大偏移量为1.459 m;4号柱双腕臂A支最大偏移量为1.492 m,4号柱双腕臂B支最大偏移量为1.28 m,4号柱双腕臂底座最小间距为1.886 m。

计算结果表明,缩短半锚长度可有效降低叠加关系时的腕臂偏移量和双腕臂底座宽度。

4 结论

(1)大跨度钢梁区段接触网建议采用本文推荐的锚段布置方式,可有效降低腕臂偏移量。

(2)整体布置在钢梁上的锚段腕臂偏移均为相减关系;应重点关注跨梁缝布置的锚段腕臂偏移问题,腕臂偏移为叠加关系时缩小半锚长度可有效减小腕臂偏移量。

(3)应特别注意跨度大于720 m钢梁伸缩缝两侧锚段关节的双腕臂间距,有条件时双腕臂建议采用双支柱安装,且双支柱间距建议按不低于2.5 m进行设计。

(4)腕臂安装曲线应根据大跨度钢梁区段锚段布置方案,判断桥梁伸缩与导线伸缩对腕臂偏移的作用关系,参考本文计算公式进行逐工点计算,以指导腕臂安装的设计、施工和运营维护。