中低速磁浮圆曲线钢箱梁桥车致振动响应研究

2024-04-12尚贤洪马卫华罗世辉

铁道标准设计 2024年4期

尚贤洪，刘宇，李苗，雷成，马卫华，罗世辉

(1.西南交通大学牵引动力国家重点实验室,成都 610031; 2.中车唐山机车车辆有限公司产品研发中心,河北唐山 063035;3.郑州铁路职业技术学院河南省轨道交通智能安全工程技术研究中心,郑州 451460)

引言

近年来,中低速磁浮交通系统在国内得到了快速发展,其具有转弯半径小、舒适度佳、运行噪声低等特点,在未来城市公共交通运输中具有良好的发展前景[1-3]。小半径曲线高架桥梁因其对复杂线路适应性好,被广泛应用于中低速磁浮的线路建设中,而采用轻型钢箱梁桥则可以有效缩短施工周期,降低线路成本,是中低速磁浮交通系统未来的发展趋势[4-5]。然而,目前钢箱梁桥大多应用于道岔结构,在曲线线路上还未能得到应用。由于钢箱梁桥的线密度和阻尼比较小,车辆与桥梁之间动力相互作用影响显著,且由于曲线桥梁受曲率影响,在发生弯曲时必然伴生扭转,这种“弯扭耦合”作用使得曲线桥梁的受力相比直线桥梁更为复杂,这给钢箱梁桥的发展带来了挑战,同时这也是中低速磁浮交通发展道路上亟待研究并解决的问题。

中低速磁浮车辆与桥梁是一个典型的强耦合非线性系统,车辆系统中主动控制的电磁力在实现车辆稳定悬浮的同时,也带来了耦合振动问题。随着对中低速磁浮交通系统研究的进一步深入,车辆-桥梁耦合动力学研究得到了研究人员的大量关注。KIM、HAN、LEE等[6-8]基于精细化的中低速磁浮车桥耦合动力学模型,研究了车辆、车速、不平顺、挠跨比和阻尼比等因素对耦合系统动态响应的影响。李小珍等[9-11]结合线路试验结果研究了F轨结构、激励位置、扣件刚度、轨枕间距等因素对车桥耦合系统振动特性的影响。王亚朋和蔺鹏臻[12]结合现场动载试验实测数据,分析了车速、车重、扣件刚度以及轨枕间距对双线简支梁冲击效应的影响。李国强等[13]研究了日照作用下磁浮钢箱梁的温度变形对车桥耦合振动的影响。ZHOU等[14]研究了中低速磁浮车辆-桥梁耦合扭转共振的基本原理,并讨论了桥梁质量、车辆载荷等对扭转共振的影响。

尽管取得了上述研究成果,但有关中低速磁浮圆曲线钢箱梁桥的研究还鲜有报道。基于上述原因,有必要对钢箱梁在中低速磁浮车辆动态作用下的振动响应特性展开数值仿真研究。建立考虑桥梁柔性影响的车辆-钢箱梁耦合动力学模型,模型中采用考虑了横向动态电磁阻尼力影响的二维磁轨关系,桥梁主体考虑为钢箱梁结构,对中低速磁浮车辆通过平面圆曲线时钢箱梁的车致振动响应特性进行分析,随后探讨钢箱梁板厚、车辆速度以及车体质量3个参数变化对钢箱梁动态响应的影响,以期为后续中低速磁浮钢箱梁的优化设计提供有益参考。

1 数值计算模型

1.1 车辆模型

运用多体系统动力学软件,建立由车体、悬浮架、防侧滚梁、吊杆、牵引拉杆、移动滑台与固定滑台等部件组成的车辆系统动力学模型,如图1所示。其中,车体由5个(悬挂)中置式悬浮架支撑,每个悬浮架分为左右2个悬浮模块,左右悬浮模块通过中间的一套防侧滚梁装置连接,防侧滚梁与悬浮模块之间具有绕z轴的转动自由度;每个悬浮模块上有4个电磁铁线圈,并设置有前后2套传感器各自控制2个电磁铁线圈,同时文献[15]指出将单个线圈的电磁力等效为3个集中力时可较好地兼顾计算精度和效率;车体下方共设置有5组滑台,其中1、3、5组滑台为移动滑台,与车体之间具有横移自由度,2、4组为固定滑台,与车体固结;吊杆与牵引杆两端均为刚性球铰约束,空气弹簧视为无质量的弹簧阻尼单元。动力学模型各刚体自由度说明见表1,整个车辆模型共计142个自由度。

表1 车辆动力学模型自由度Tab.1 Degrees of freedom of vehicle dynamic model

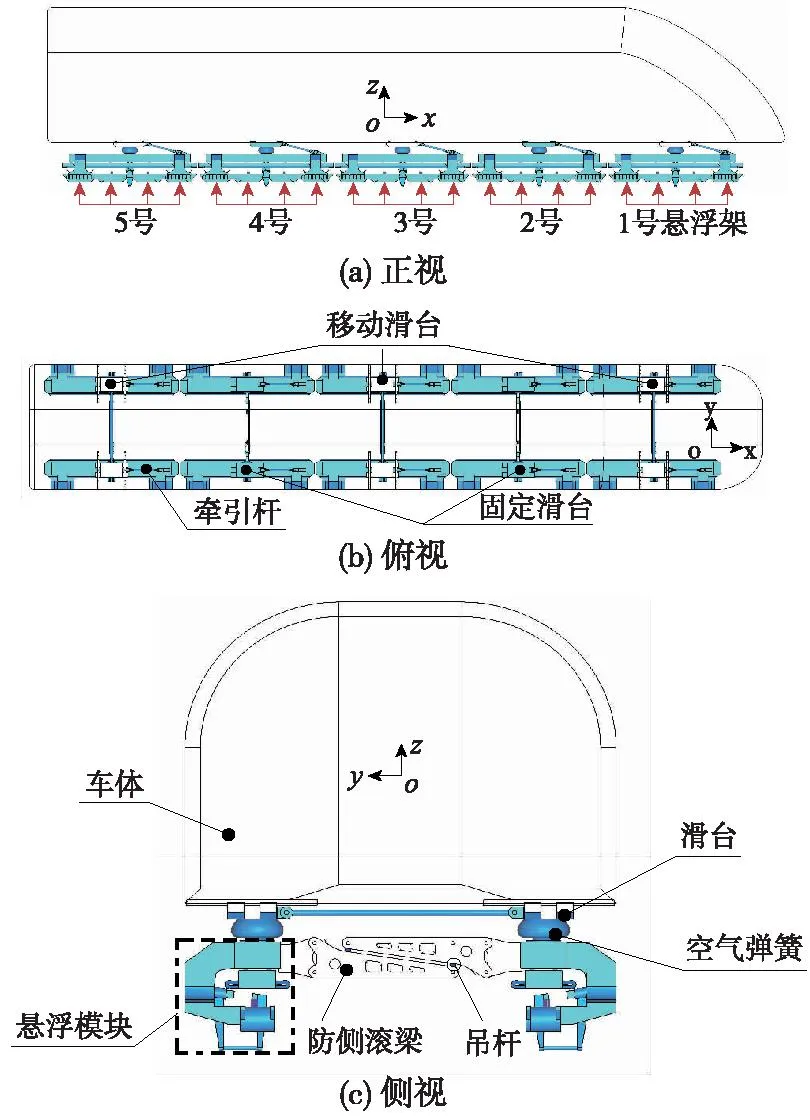
图1 (悬挂)中置式中低速磁浮车辆模型Fig.1 Model of medium-low-speed maglev vehicle using levitation frame with mid-set air spring

1.2 悬浮控制模型

根据电磁理论,若不考虑导磁体磁阻、电磁回路中漏磁,则电磁铁与F轨之间的电磁力Fe可表示为

(1)

式中,μ0为真空磁导率;N为电磁铁线圈匝数;A为有效磁极面积;i为电磁铁电流;z为悬浮间隙。

电磁铁线圈电流实际由控制电压驱动,控制电压同时驱动2个电磁铁线圈。根据基尔霍夫定律,线圈电流i与控制电压U之间的关系可写成

(2)

式中,R为电路电阻;其余符号含义见式(1)。

由于电磁力本身存在固有的不稳定特性,需要对悬浮电磁铁电流进行主动控制以实现稳定悬浮,目前应用最多的悬浮控制算法为对悬浮间隙偏差、垂向振动速度和垂向振动加速度3个状态量进行加权反馈的PID控制。考虑到实际工程应用中,悬浮间隙与振动加速度信号可以由传感器同时测得,而难以测得振动速度信号,此处根据Luenberger观测器理论引入状态观测器来构建速度信号[16]

(3)

式中,z和a分别为传感器实测的悬浮间隙和垂向振动加速度;ξ0和ω0分别为观测器的阻尼比和特征频率;δ和θ分别为观测的悬浮间隙和垂向振动速度。

进一步通过“位移-速度-加速度”反馈得到目标悬浮电流ie,并使用电流环反馈以加快电流跟踪速度

(4)

U=ke(ie-i)+2Ri

(5)

式中,kp、kd、ka、ki、ke、i0、z0分别为间隙反馈系数、速度反馈系数、加速度反馈系数、积分系数、电流反馈系数、额定悬浮电流、额定悬浮间隙。

中低速磁浮车辆由于其运行速度较低,没有配置导向电磁铁用于主动导向,而是通过U形电磁铁与F轨之间发生横向错位时产生的电磁力横向分力进行被动导向。参考文献[17],当电磁铁与F轨之间存在横向错位时,横向方向上的导向力Fy与垂向方向上的悬浮力Fz可表示为

(6)

式中,Wm为单侧磁极宽度;y为电磁铁横向偏移。

从式(6)来看,悬浮力的计算公式可以通过反馈控制为悬浮模块提供一定的垂向悬浮刚度和阻尼,而导向力的计算公式则只能为悬浮模块提供横向的导向刚度[3]。这意味着使用式(6)进行仿真计算时,当悬浮模块遇到横向激扰发生横移或摇头时,系统会持续振荡而无法收敛。考虑到实际的列车运行中,悬浮模块在受到横向激扰后会逐渐收敛至平衡位置,为保证车辆曲线通过时的横向稳定性,在导向力计算中引入了动态的电磁阻尼力Fv。这一阻尼力主要由电磁铁相对轨道横向运动时,轨道内产生的涡流与磁场相互作用而形成的安培力提供[18]

(7)

式中,l为电磁铁计算长度;d为轨道单侧高度;σ0为电导率;v为电磁铁横向运动速度。

1.3 钢箱梁模型

文献[9]指出,在仿真分析中F轨对车桥系统耦合振动响应的影响不可忽略。因此,基于有限元方法建立长16 m的包含F轨、轨枕、钢箱梁的轨道-钢箱梁系统有限元模型(结构尺寸见图2,钢箱梁为基于道岔结构型式的箱形梁结构,其中梁高为1.5 m,h为钢箱梁板厚),其中圆曲线半径为70 m,横坡角为6°。

图2 钢箱梁断面结构尺寸(单位:mm)Fig.2 Dimension of steel box girder structure (unit: mm)

在该模型中,F轨、轨枕、钢箱梁等均为钢结构,弹性模量取206 GPa,泊松比取0.3,密度取7 840 kg/m3,F轨采用Solid185单元模拟,轨枕和钢箱梁采用Shell63单元模拟。F轨与轨枕固结,轨枕与承轨台之间的扣件通过弹簧力元模拟,钢箱梁主体采用简支约束,桥梁支座同样通过弹簧力元模拟。使用一致质量矩阵和瑞利阻尼构建轨道-钢箱梁系统的质量和阻尼矩阵,由于轨道-钢箱梁系统均为钢结构,取该系统的模态阻尼比为0.01。

为探究轨道-钢箱梁的自振特性,表2给出了不同板厚h下钢箱梁系统的线密度ρ和自振频率f,轨道-钢箱梁系统的主要模态振型见图3。计算得到系统的一阶竖弯频率显然满足TB 10630—2019《磁浮铁路技术标准(试行)》中桥梁竖向一阶固有频率不低于90/L(L为桥梁计算跨距,L=15 m)的规定,表明轨道-钢箱梁系统具有足够的垂向刚度。

表2 不同板厚下轨道-钢箱梁系统的线密度与自振频率Tab.2 Linear density and natural vibration frequency of track-steel box girder system with different thickness

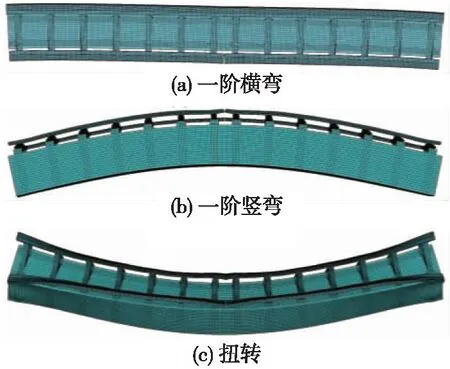
图3 轨道-钢箱梁系统模态Fig.3 The modal of track-steel box girder system

1.4 动力相互作用模型求解

建立的车辆-轨道-钢箱梁耦合系统可视化动力学模型如图4所示,车辆系统动力学模型与轨道-钢箱梁系统有限元模型通过磁轨关系耦合,并在UM中采用基于二阶变步长隐式求解器进行数值计算,该方法可有效求解刚柔耦合模型中包含的刚性微分-代数方程。

图4 车辆-轨道-钢箱梁耦合系统可视化动力学模型Fig.4 Visualized dynamics model of the vehicle-track-steel box girder coupled system

2 钢箱梁振动特性分析

2.1 工况设置

为更深入地研究圆曲线钢箱梁桥的振动特性,对空载车辆(车体质量14 t)以30 km/h速度通过圆曲线钢箱梁(板厚h=20 mm)工况进行仿真计算。由于当前中低速磁浮轨道不平顺实测数据较少,故轨道不平顺功率谱函数[19-21]为

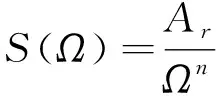
(8)

式中,Ar为表面粗糙度系数,取8×10-7m;Ω为空间波数,取3 000 rad/m;n为频率特征参数,取2。对功率谱函数进行反演,设置波长范围为0.5～50 m,得到所需的轨道不平顺样本,如图5所示,高低不平顺幅值不超过±4 mm。

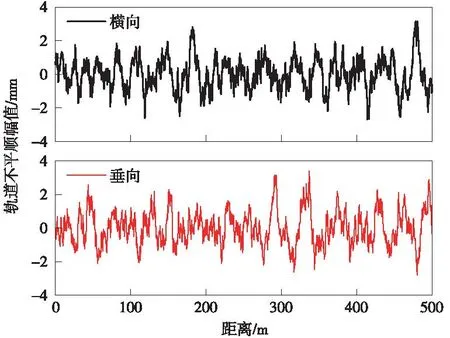
图5 轨道不平顺样本Fig.5 Samples of track irregularity

2.2 振动特性分析

为探究圆曲线钢箱梁的振动特性,图6给出了钢箱梁跨中的振动加速度响应时间历程以及加速度频谱。由图6(a)可知,钢箱梁跨中横向与垂向加速度幅值分别为0.8,0.6 m/s2,均未超过铁运函[2004]120号《铁路桥梁检定规范》中规定的横向加速度限值1.4 m/s2及TB 10002—2017《铁路桥涵设计规范》中规定的垂向加速度限值5.0 m/s2。由图6(b)可知,钢箱梁加速度的优势频率主要集中在10～20,30～40 Hz和50～70 Hz范围内。其中,10～20 Hz为钢箱梁的整体弯曲振动频段,该频段内横向加速度振幅最大值对应频率为11.9 Hz,接近钢箱梁的一阶横弯频率;垂向加速度振幅最大值对应频率为15.5 Hz,接近钢箱梁的一阶竖弯频率;30～40 Hz为钢箱梁的扭转振动频段,该频段内横向加速度与垂向加速度振幅最大值对应频率均为34.1 Hz,接近钢箱梁的扭转频率,这表明钢箱梁的扭转振动会同时影响横向以及垂向的振动加速度响应;50～70 Hz为轨道局部振动频段,该频段内横向加速度振幅最大值对应频率为59.8 Hz,轨道局部振动主要表现为F轨的横向振动,钢箱梁垂向加速度受轨道局部振动影响较小。

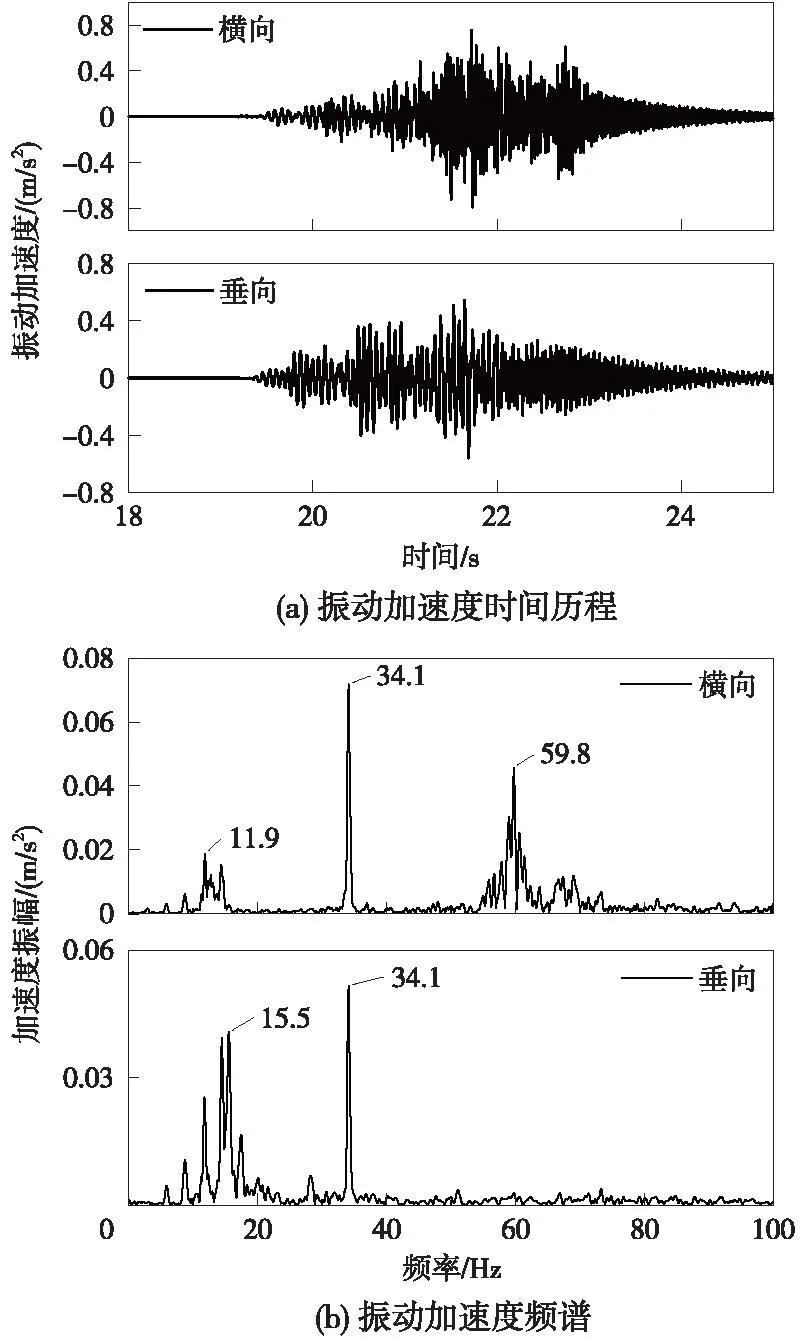
图6 钢箱梁跨中振动特性Fig.6 Vibration characteristics of steel box girder at the mid-span

综上可知,圆曲线钢箱梁桥受曲率影响,在发生横向或垂向弯曲的同时亦会伴生扭转,即产生“弯扭耦合”振动。20 Hz以内的低频振动加速度主要由钢箱梁的整体弯曲振动产生,50 Hz以上的高频振动加速度主要由轨道局部振动导致,30～40 Hz范围内的振动则主要由钢箱梁的扭转振动引起,且扭转振动对于横向及垂向的振动加速度均有较大贡献。

3 参数分析

3.1 车辆速度的影响

为分析中低速磁浮车辆通过钢箱梁时,车速变化对钢箱梁动态响应的影响,选取通过速度20～38 km/h(对应未平衡离心加速度的范围为-0.6～+0.6 m/s2)进行了仿真计算。空载车辆作用、不同板厚、不同车速影响下钢箱梁跨中的动态响应计算结果见图7。

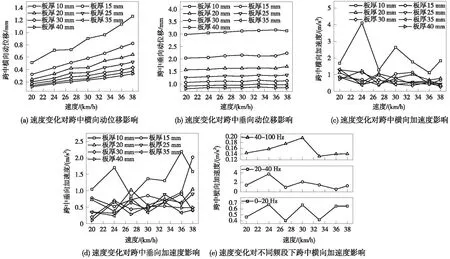
图7 速度变化对钢箱梁动态响应的影响Fig.7 Dynamic response of steel box girder varying with speed

由图7(a)、图7(b)可知,不同板厚、车速下的钢箱梁跨中横向及垂向动位移最大值分别为1.26 mm、3.17 mm,均不超过CJJ/T 262—2017《中低速磁浮交通设计规范》中规定的桥梁横向变形容许值L/2 000=7.50 mm和垂向变形容许值L/3 800=3.95 mm,这表明钢箱梁具有足够的刚度支撑车辆。

由图7(c)、图7(d)可知,跨中横向和垂向加速度幅值总体上随板厚增大而减小,随着车速增大,垂向加速度幅值总体上呈上升趋势,但并未超过垂向加速度限值5.0 m/s2;而横向加速度幅值却随车速增大呈现下降趋势,即过超高下的钢箱梁横向振动大于欠超高,而过超高下车辆所受离心力小于重力分量,钢箱梁受到曲线内侧横向拉力,这说明了钢箱梁在曲线内侧横向拉力作用下的振动响应会更加剧烈。

此外,板厚越小、通过速度越低,横向加速度幅值也越大,其中板厚10 mm钢箱梁的跨中横向加速度幅值最大达到4.0 m/s2,远超横向加速度限值1.4 m/s2。以板厚10 mm的钢箱梁为例,对不同速度下跨中横向加速度进行带通滤波,结果见图7(e)。显然,产生这一现象的横向加速度优势频率位于20～40 Hz范围内,结合表2与2.2节分析结果,可以确定是由钢箱梁的扭转振动引起。研究表明:扭转振动对于圆曲线钢箱梁的横向振动有较大影响,且随着线密度及车速降低,扭转振动的影响愈发显著,钢箱梁的横向振动也愈发剧烈。

3.2 车体质量影响

为研究车体质量变化对钢箱梁动态响应的影响,选取车辆空载、座客、定员、超员4种载荷工况,分别对应车体质量14,16,20,23 t,以均衡速度30 km/h匀速通过钢箱梁。不同板厚、车体质量下钢箱梁跨中的动态响应结果见图8。

图8 车体质量变化对钢箱梁动态响应的影响Fig.8 Dynamic response of steel box girder varying with mass of the car body

由图8(a)、图8(b)可知,不同板厚、车体质量下的钢箱梁跨中横向及垂向动位移最大值分别为1.25,3.88 mm,均满足相关标准规定,这表明钢箱梁有足够的刚度以支撑车辆。

由图8(c)、图8(d)可知,钢箱梁跨中横向和垂向加速度幅值总体上随板厚增大而减小,随车体质量的增大而增大。其中垂向加速度幅值符合相关标准中的规定,而横向加速度幅值在板厚10 mm以及超员载荷工况下大多超过1.4 m/s2,出现较为强烈的车桥耦合振动现象。进一步对钢箱梁横向振动加速度的频谱(图8(e))进行分析可知:车体质量的增加会增大加速度各阶频率对应的振幅;而板厚从10 mm增大至40 mm时,一阶横弯频率及扭转频率对应振幅分别减小94.3%、98.7%。可以看出,车体质量的增加会放大弯扭耦合作用的影响;而增加钢箱梁板厚则可以有效降低弯扭耦合作用的影响。