高速铁路接触网腕臂系统的力学特性
2021-06-06刘金增刘志刚储文平
张 静 ,刘金增 ,刘志刚 ,储文平
(1. 西南交通大学机械工程学院,四川 成都 610031;2. 西南交通大学电气工程学院,四川 成都 610031)
随着高速铁路的迅速发展,对高速铁路接触网安全运营的要求也越来越高. 弓网的动态性能决定了电能传输的可靠性和供电质量. 接触网具有大跨度、高柔性的特点,对外部荷载的扰动非常敏感,在外部荷载(风载、覆冰、受电弓抬升力等)的作用下,接触网会出现振动现象[1-7]. 过大的振动会导致弓网系统的受流性能恶化,更容易引起接触网系统疲劳、受电弓离线等问题,严重时,甚至会发生刮弓事故.腕臂是接触网的支撑装置,对接触网起支持和定位作用,并且承受电气和机械载荷. 接触线和承力索承受的环境载荷会传递到腕臂,容易引起腕臂的疲劳和破坏.
目前,国内外学者对腕臂做了大量研究,但这些研究主要集中在接触网腕臂的检测方面[8],对腕臂的有限元分析计算不是很多,并且腕臂有限元计算都存在不同程度的简化[9-12]. 文献[10]腕臂结构的有限元模型采用梁单元BEAM188建立的,并编制了平腕臂的参数化分析程序,完成腕臂的模态分析. 文献[11]采用BEAM188建立有限元模型,对腕臂进行静力学和动力学分析,得到腕臂的最大应力和腕臂的模态以及谐响应分析,但衔接处的连接件(螺栓、定位环等)是一种简化结构. 文献[12]采用互推方法,给出一种腕臂系统应力传递的研究方法,并用试验完成有限元模型的验证. 但这些文献的研究都忽略了螺栓以及套管双耳等连接件对腕臂的影响,也都未考虑不同的环境荷载对腕臂应力水平的影响,使得腕臂系统分析计算结果不够准确.
本文以高速铁路接触网正定位腕臂系统为研究对象,建立了一种新的腕臂有限元模型. 对腕臂不同环境荷载下的静力分析,得到最大应力点分别在平腕臂和斜腕臂连接处的螺栓处和定位线夹处,此处为结构的薄弱点;通过对腕臂的动力学分析得到腕臂的固有频率和振型,为腕臂设计和工作时避免共振提供依据;推导了载荷在腕臂系统中的传递规律和力传递到支柱的分布,为腕臂设计时的载荷合理分布提供参考依据. 最后,通过腕臂装置的静力学和动力学试验结果和仿真结果的比较,验证了腕臂结构有限元模型的正确性,完成了腕臂系统的力学特性研究.
1 腕臂静力学分析
采用二次位移模式实体单元,建立腕臂的有限元模型如图1所示. 有限元模型中考虑了套管双耳和螺栓等连接件,为模拟定位线夹处的弹性约束,在定位线夹处施加弹簧约束. 在定位器与定位器支座连接处、定位管和斜腕臂连接处、平腕臂和上底座连接处以及斜腕臂与下底座连接处设置铰接,如图2所示,并在腕臂上下底座设置固定约束. 图中:Lx、Ly、Lz分别为x、y、z轴的平移自由度;Rx、Ry、Rz分别为x、y、z轴的旋转自由度.
接触网采用“TM-120+CTM-150”全补偿链形悬挂,跨距为50 m. 计算不同风速、不同覆冰厚度下腕臂的应力和变形分布. 根据接触网网页载覆冰负载和“之”分布的计算理论,得到腕臂不同工况下的荷载如表1所示. 将载荷和约束施加到腕臂有限元模型,得到腕臂在不同工况下的计算结果如图3所示.

图1 腕臂有限元模型Fig. 1 Finite element model of cantilever
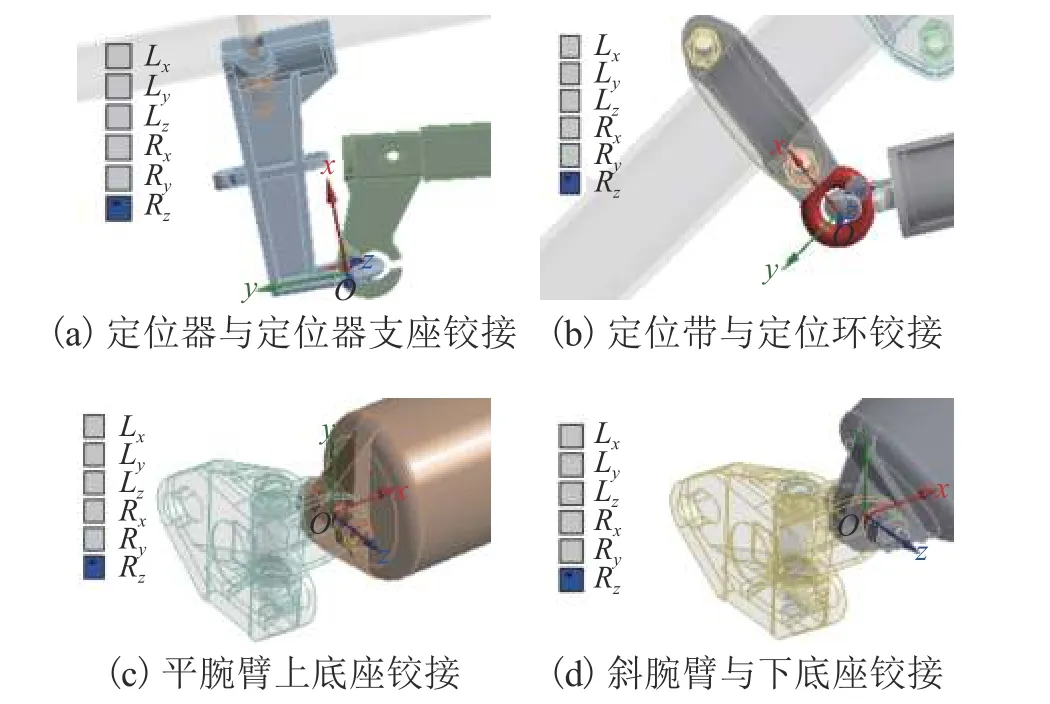
图2 腕臂中的旋转连接Fig. 2 Cantilever rotation connection

表 1 腕臂载荷Tab. 1 Cantilever load N

图3 不同工况下腕臂的有限元计算结果Fig. 3 Finite element calculation value of cantilever with different working conditions
由图3可知:在不同的环境荷载下,腕臂的最大应力点不同,覆冰载荷时最大应力点在斜腕臂和套管双耳连接处的螺栓处,静风荷载时最大应力点在定位线夹处. 在不同的环境荷载时,腕臂不同的受力点的荷载变化不同. 覆冰荷载主要以重力的形式作用到腕臂承力索座处,且为垂直向下的荷载,静风载荷作用在承力索、接触线和吊弦处,并通过承力索座和定位线夹传递到腕臂.
腕臂的最大位移均在定位线夹处,主要由于定位器能够绕定位器支座旋转,且定位线夹处的约束为弹簧约束,此处的位移为定位器绕定位器支座旋转后的位移变形,包括定位器的弹性变形和刚体位移.
2 腕臂动力学分析
2.1 模态分析
采用ANSYS Workbench软件,完成腕臂的整体模态分析,获得模型的前10阶固有频率,计算结果如表2所示.

表 2 腕臂前10阶固有频率Tab. 2 First ten order natural frequencies of cantilever Hz
由表2可知:腕臂固有频率从4.230 Hz不断增加, 第1阶振型的固有频率最小,在低阶振动时载荷的能量比较强,振动比较容易激发. 腕臂前6阶振型如图4所示.

图4 腕臂系统前6阶模态振型Fig. 4 First six order vibration mode shape images of cantilever system
由图4所示,腕臂系统在不同的阶数时其振型不同:第1、2、3阶振型下的腕臂在定位线夹处有较大的空间振动位移,第4、5、6阶振型下的腕臂在定位管的端点处有较大的空间振动位移.
图4所示的变形是腕臂模型各个节点之间的变形的相对量,显示了各节点间的振动传递情况. 在振动中,腕臂各个杆件之间的夹角会发生变化,这将直接导致各个杆件的相位差发生改变,从而产生惯性力和惯性力矩,对腕臂工作的安全稳定性产生不良影响,导致各个杆件之间的相对位移发生变化,这将直接导致腕臂的结构会发生变化,同时,也会导致连接处的螺栓松动,这将对腕臂的安全可靠性带来巨大的隐患.
2.2 载荷传递规律
考虑定位器和定位器支座之间的刚度、阻尼和摩擦等因素,建立了定位线夹通过定位器传递到定位器支座的响应模型,如图5所示. 图中:Fz为外部激励载荷;Cj为关节处的阻尼;Kj为关节处的连接刚度;Ff为关节连接处的摩擦;Fq为外部激励载荷传递到挂接另一侧的载荷.
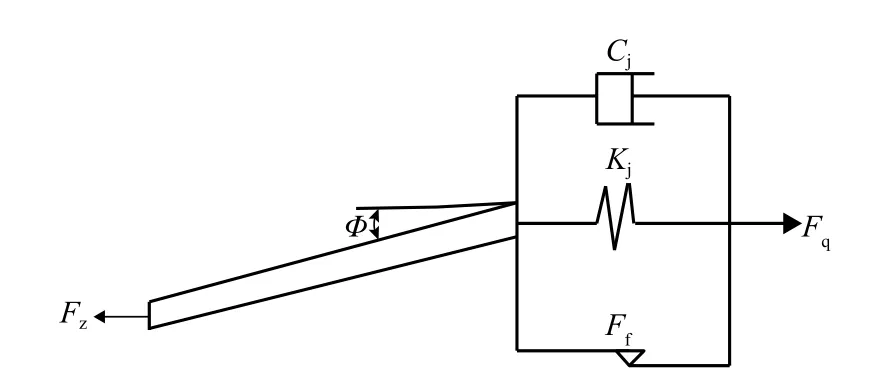
图5 定位器铰接模型Fig. 5 Articulation model of steady arm
研究载荷传递到腕臂底座的分布规律,建立力学模型可以对不同时速下腕臂的载荷传递规律进行研究.
由于铰链非线性接触特性中恢复力具有奇函数特性,故可对恢复力拟合两组只包含奇次项的多项式,用一次项和三次项表示恢复力FRF的非线性函数,如式(1).

式中:k1和k3分别为恢复力中一次项和三次项的刚度系数,恢复力中的刚度系数可有试验数据拟合得到;xj为关节处的位移.
当定位器在受到外部振动时,由于定位器和定位器支座的工作状态,其铰链仅存在接触一种状态.铰链在自由运动阶段惯性力与外部激励相平衡,在受拉阶段除了铰链的惯性力外,还受到黏性阻尼力、摩擦力和接触力的作用. 因此,考虑阻尼、摩擦和非线性恢复力时,铰链的非线性动力学方程为

式中:J为定位器绕铰链的转动惯量;m为定位器质量;L为定位器的长度.
方程中考虑了定位器转动、铰接处的摩擦、阻尼和刚度对载荷传递的影响.
图6为腕臂的杆件简化模型,显示了腕臂各个部分的长度和角度. 图中:F为腕臂整体受到的外力.DE杆为腕臂支撑,仅受到轴力作用,将DE杆的轴力用F3和F4表示,腕臂的载荷F1~F8如图7所示.
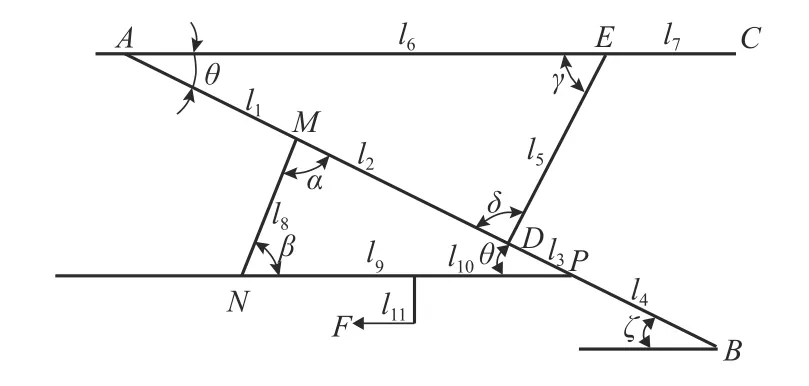
图6 腕臂杆模型Fig. 6 Bar model of cantilever
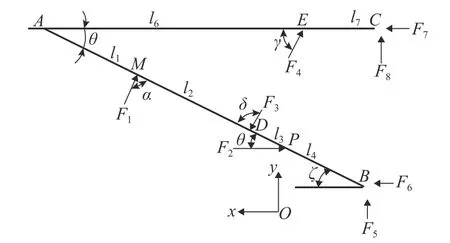
图7 腕臂载荷模型模型Fig. 7 Load model of cantilever
腕臂上框架ABC结构为超静定结构,忽略杆DE的轴向变形,通过变形叠加,在F1、F2、F3的作用下DP段的变形方程如式(3).
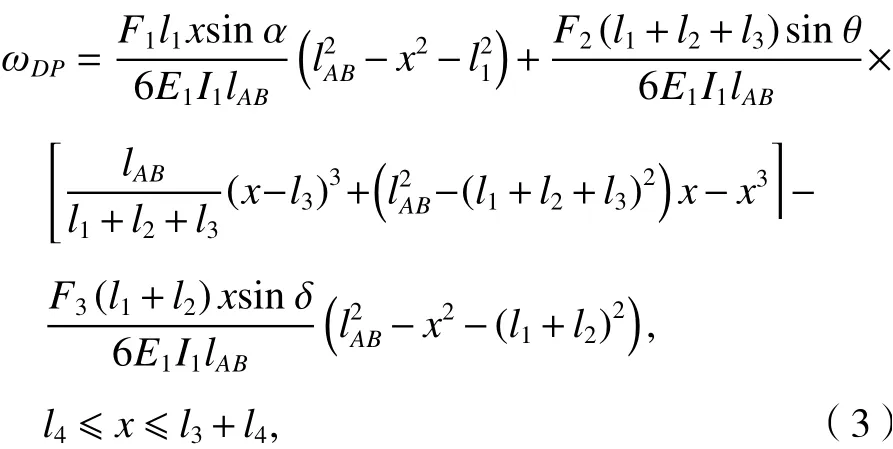
式中:E1为斜腕臂的弹性模量;I1为斜腕臂的惯性矩;lAB为斜腕臂AB的长度;ωDP为位移变形函数,后同.
式(3)可简化为

式中:
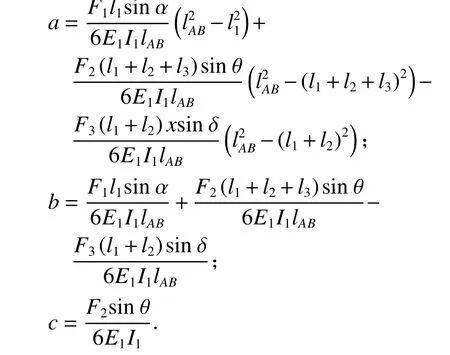
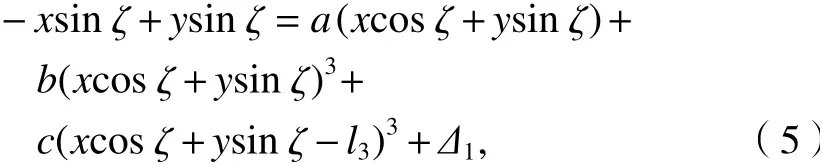
式中:Δ1为杆AC和杆AB的变形对杆AB影响的位移变形量.
同理杆AC的位移变形方程如式(6)所示.
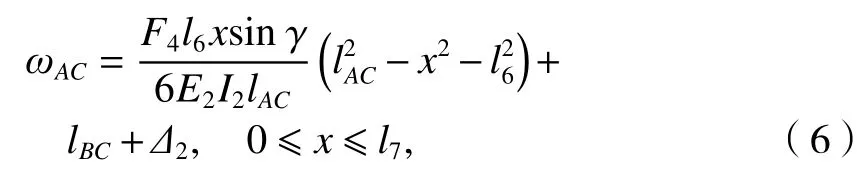
式中:E2为平腕臂的弹性模量;I2为平腕臂的惯性矩;lAC为平腕臂AC的长度;Δ2为杆AC的位移变形量.
通过联立式(5)和(6),根据杆DE的长度不变的假设,可得到
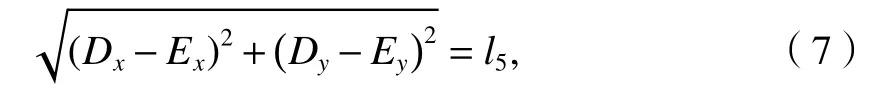
式中:Dx、Dy和Ex、Ey分别为点D和点E的x和y方向的位移.
解出F3、F4,从而框架结构ABC就可以以一个静定结构得到F5~F8的值,得到定位器上的载荷传递到腕臂底座的规律.
本例中腕臂圆管的外径为60 mm,内径为50 mm,材料为不锈钢,在定位器处施加式(8)的正弦形式水平载荷F,得到在正弦载荷下腕臂的响应.
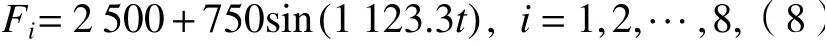
式中:t为时间.
本方法计算得到的F5~F8的值和有限元方法得到结果的对比如图8所示.

图8 计算结果和仿真结果对比Fig. 8 Comparison between calculation value and simulation value
由图8可知:仿真值的振幅大于计算值的振幅,主要原因是仿真数据中考虑了腕臂的摩擦、阻尼和接触刚度等因素,但是计算式中并未完全考虑这些因素. 在曲线稳定后,计算值和仿真值的吻合性较好.
3 试验验证
腕臂系统试验采用钢腕臂,图9(a)为腕臂试验安装图,图9(b)为腕臂的施加荷载图. 试验分为两个部分,首先测试腕臂在静态载荷下的静态应变,通过疲劳试验机对腕臂施加水平方向2.5 kN的静态应力,然后施加动态荷载,测试腕臂在动态载荷下的动应变.

图9 腕臂试验Fig. 9 Cantilever test
在关键部位布置相应的应变片,采集试验过程中静态和动态应变数据,腕臂装置采样点分布和应变片如图10所示.
采集静态试验结果并与有限元仿真结果对比,如表3所示. 由表3可知:测点 ①~⑦ 的测试值和计算仿真值的误差在可接受的范围内. 故可认为,在静态时,腕臂的试验结果和仿真结果一致.
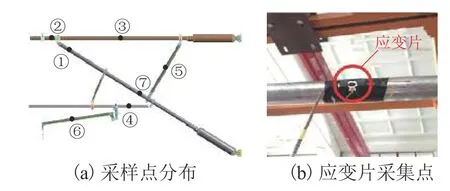
图10 腕臂静力学试验Fig. 10 Cantilever statics experiment
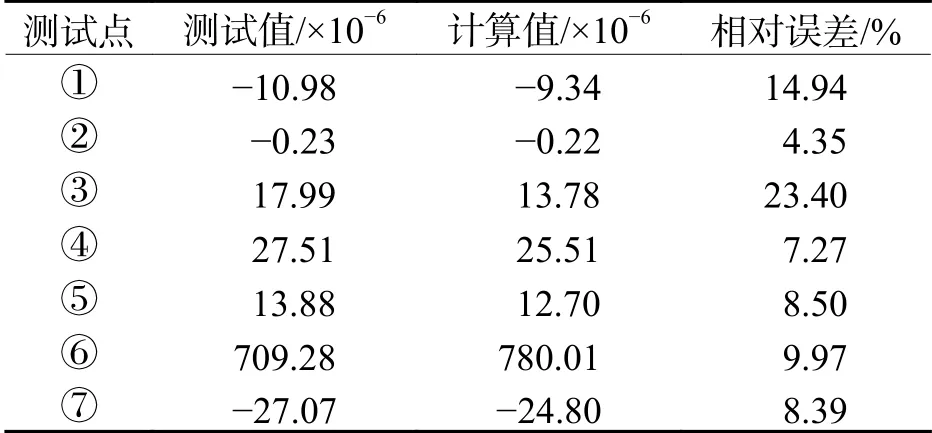
表3 腕臂装置静态强度试验与仿真结果对比Tab. 3 Comparison of static strength test and simulation results of cantilever
动力学试验采样点布置和静态试验相同,通过疲劳试验机对腕臂施加式(8)的载荷.
在腕臂结构振动平稳后采集动态应变数据,采集相同时段的数据,将仿真结果和试验结果对比,结果如图11所示.

图11 测点 ①、③、④、⑦ 仿真和试验结果对比Fig. 11 Comparison of simulation and test value of measuring points ①,③,④ and ⑦
由图11可知,由于在仿真时未考虑套管双耳等部件的滑动以及有可能发生的螺栓松动,在进行腕臂振动台架试验时,由于腕臂装配以及其他因素的影响下,试验时的振动较为剧烈,使得测试数据的幅值相较于仿真数据较大,但测试数据和仿真数据的平均值、趋势以及振动频率相同. 通过对腕臂结构静态和动态的试验和仿真结果的对比可以得出:腕臂结构仿真和试验结果数据比较吻合,仿真结果是真实可信的.
4 结 论
1) 考虑螺栓、套管双耳等连接件对腕臂的影响,建立了腕臂的实体有限元模型. 得到了腕臂在不同工况下的最大应力点和应力分布图,为腕臂的优化设计提供思路.
2) 腕臂在振动时定位器的振动幅值较大,相比与其他部位振动剧烈,并结合静态分析的结果,得到定位器处容易产生疲劳损伤.
3) 通过数值计算和仿真计算,载荷从定位点处传递到腕臂底座的传递路径及其各杆件之间的载荷传递规律. 在腕臂优化设计时,为腕臂中载荷的合理分布提供依据.
4) 通过台架试验验证了有限元模型的正确可靠性,同时也为其他型号腕臂的试验提供参考依据.
