单轨吊起吊马达同步控制联合仿真分析
2024-04-12沈宗果张锐丽
沈宗果, 张锐丽, 吴 凯
(1.南阳农业职业学院 数字信息中心, 河南 南阳 473000; 2.宜宾职业技术学院 现代制造工程系, 四川 宜宾 644003; 3.成都理工大学 机电工程学院, 四川 成都 610059)
引言
近年来,随着国内能源结构的调整,煤炭作为消耗性能源,依然占据接近50%的全部消耗性能源[1],国内对于煤炭的需求量依然较大。煤矿辅助运输设备,是煤炭生产过程中极为重要的环节[2-4]。单轨吊作为煤矿井下运送材料、设备和人员的重要辅助运输设备,具有运输效率高、操作简单和应用范围广阔等特点[5-6]。目前,单轨吊主要通过驾驶人员操作手柄手动调节行驶速度,随着矿井智能化技术的发展,单轨吊的智能化远程控制将逐渐取代传统人工手柄控制成为发展的主要方向[7]。由于没有驾驶人员的手动控制,对单轨吊面对偏载启动、负载突变和系统调速的自适应性能提出了更高要求。
对于单轨吊起吊液压系统,由于起吊时负载较大,若采用单个驱动马达进行驱动,则必须增大起吊马达排量,起吊马达体积和重量也会随着增加,不利于提高单轨吊起吊性能。因此,大多采用多个起吊马达进行驱动[8-9]。由于起吊环境复杂和轨道幅度变化较大,容易对起吊系统产生冲击,严重时可能会引起起吊系统故障并带来安全事故,直接影响单轨吊正常工作效率。因此必须对起吊马达进行同步控制,以提高单轨吊起吊系统面对偏载启动、负载突变和系统调速时的自适应性。对于液压系统的同步控制研究[10],许多学者将算法结合PID控制引入液压系统[11-15],有效的改善液压系统的同步控制性能。
本研究针对单轨吊起吊液压系统,将BP神经网络引入PID控制器,构建BP-PID控制器,以提高单轨吊起吊液压系统面对偏载启动、负载突变和系统调速时的自适应性。运用AMESim和MATLAB/Simulink建立联合仿真模型,并与PID控制进行比较分析系统偏载启动特性、抗负载突变特性和调速特性。
1 系统工作原理分析
1.1 液压系统原理分析
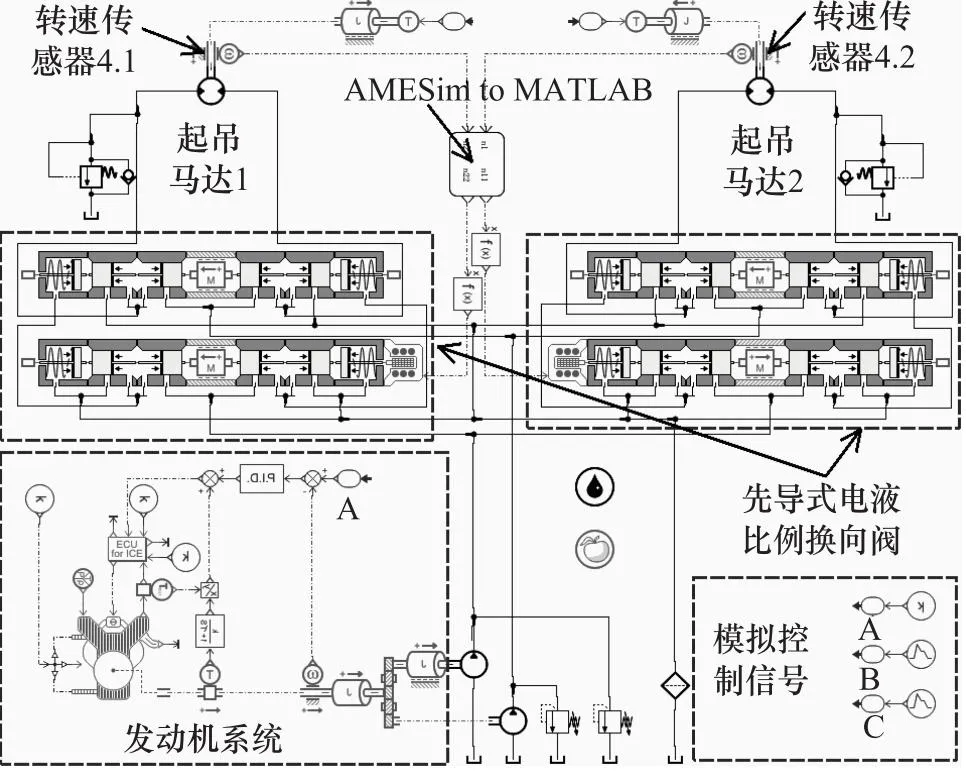
如图1所示,当先导式电液比例换向阀3.1和3.2在左位或右位工作时,从发动机1带动主泵2.1和辅助泵2.2转动产生高压油,主泵2.1出来的高压油,分别进入先导式电液比例换向阀3.1和3.2。辅助泵2.2产生的高压油用于先导式电液比例换向阀3.1和3.2先导控制。通过先导式电液比例换向阀3.1和3.2的高压油分别进入起吊马达1和2,从起吊马达1和2出来的低压油通过过滤器9流回油箱6。转速传感器4.1和4.2实时采集起吊马达1和2实际转速,并将信号传给同步控制器8,经同步控制器8处理后,将控制信号分别传给先导式电液比例换向阀3.1和3.2,使得起吊马达1和2转速同步。
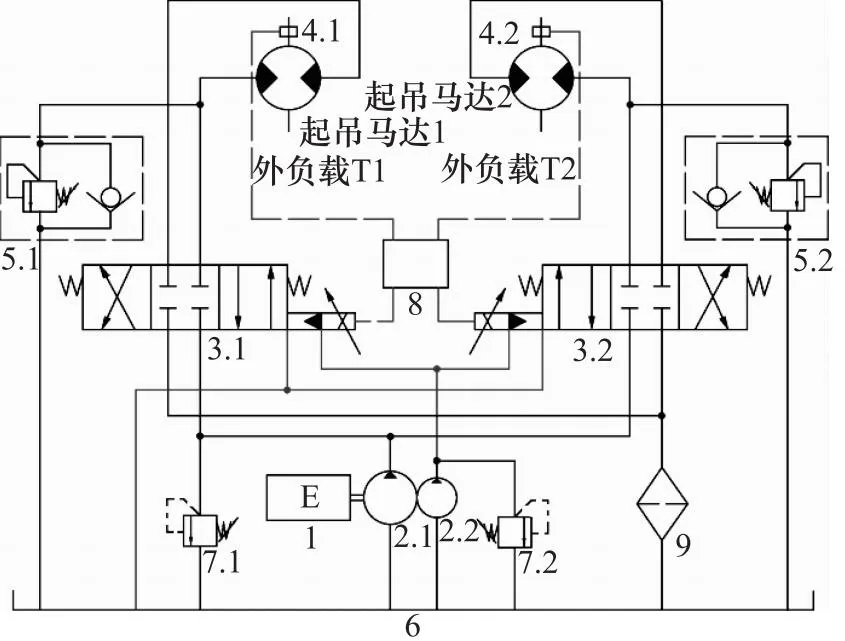
1.发动机 2.1、2.2.液压泵 3.1、3.2.先导式电液比例换向阀 4.1、4.2.转速传感器 5.1、5.2.平衡阀 6.油箱 7.1、7.2.安全阀 8.同步控制器 9.过滤器
1.2 转速控制原理分析
取先导式电液比例换向阀3.1和3.2分析压力,则:
Δpn=p泵-pn
(1)
式中, Δpn—— 先导式电液比例换向阀阀前阀后压差
p泵—— 主泵的出口压力
pn—— 先导式电液比例换向阀阀后压力
n—— 先导式电液比例换向阀序号,n=1,2
取先导式电液比例换向阀3.1和3.2分析流量,则:
(2)
式中,qn—— 通过主阀阀芯流量
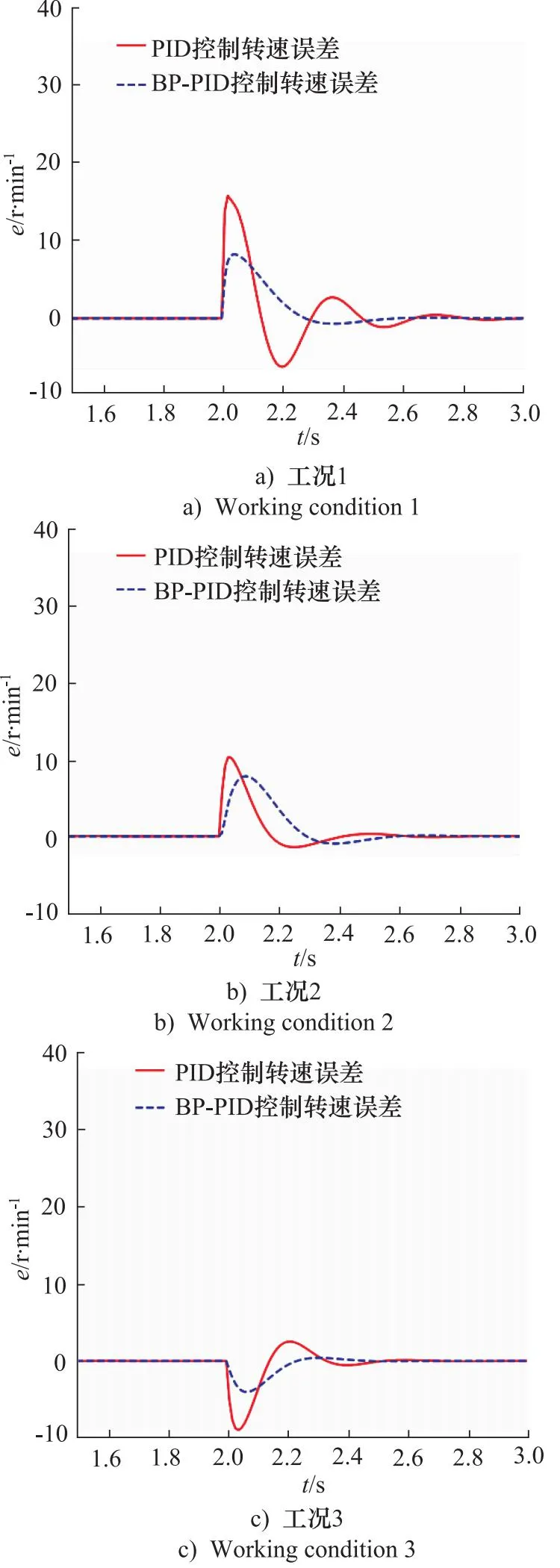
Cdn—— 流量系数
An—— 主阀阀芯开口面积
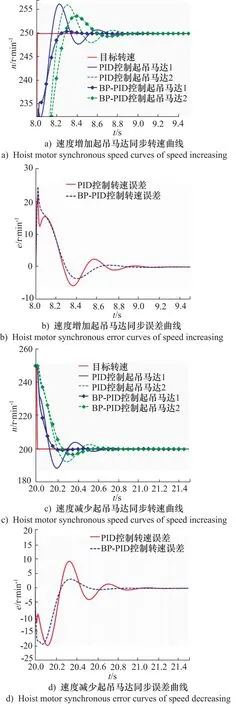
m—— 指数
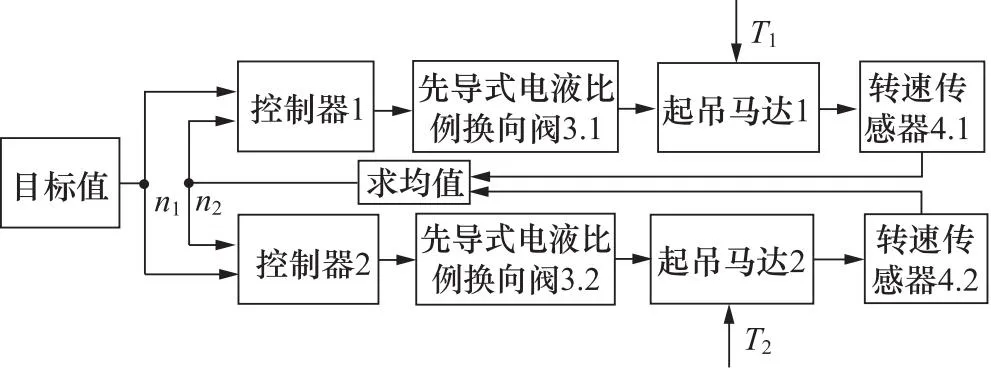
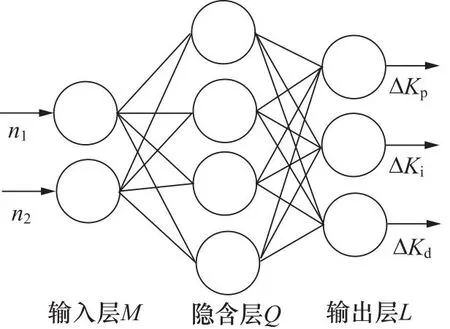
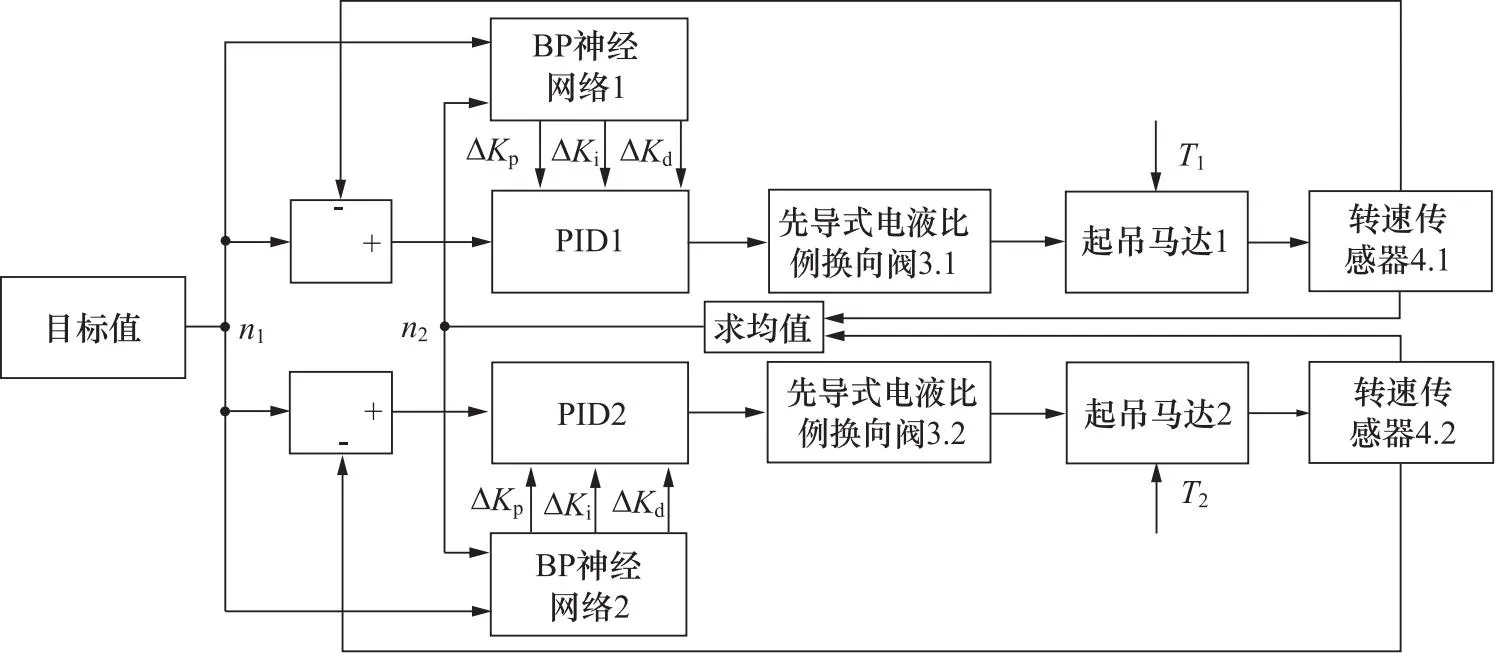
实现起吊马达1和2转速同步,即需要q1=q2,由式(1)可知,当外负载T1等于外负载T2时,即p1=p2,则Δp1=Δp2,由式(2)可知,当A1=A2时,即q1=q2,起吊马达1和2转速同步。由式(1)可知,当外负载T1大于外负载T2时,即p1>p2,则Δp1>Δp2,由式(2)可知,当A1 本研究采用耦合同步控制策略,耦合同步控制是考虑自身与相邻支路运行状态的一种同步控制策略[16]。如图2所示,系统将设定目标值n1和实际转速均值n2别输入控制器1和2,控制起吊马达1和2转速。转速传感器4.1和4.2分别采集起吊马达1和2实际转速,求出均值并分别输入控制器1和2,实现闭环控制,从而实现起吊马达1和2转速同步。 图2 耦合同步控制策略 如图3所示,BP神经网络由输入层、隐含层和输出层组成,内部信号可以在这3层内进行双向传递。因此,可以将起吊马达1和2目标转速n1和实际转速均值n2作为BP神经网络输入,比例、积分、微分系数ΔKp,ΔKi,ΔKd作为BP神经网络输出[16]。 图3 BP神经网络原理 输入层输入为: (3) (4) 式中,M—— 输入变量个数 隐含层输入为: (5) (6) f(x) —— 双曲正切函数 输出层输入为: (7) (8) 则BP输出为: 对于初创企业的绩效,不能单一使用编码的条目数来确定(吕兴群,2016[26]),因此,在访谈过程中,由企业创始人或高管团队根据企业实际,结合行业发展水平,判定企业的绩效水平,其典型例证如表8所示。 (9) (10) (11) 如图4所示,BP神经网络将目标转速n1和实际转速均值n2作为输入,通过BP神经网络对系统进行学习来整定ΔKp,ΔKi和ΔKd,从而控制先导式电液比例换向阀3.1和3.2,实现起吊马达1和2转速同步。 图4 BP-PID控制原理 本研究根据Kolmogorov定理,设计3层神经网络结构,其中输入层为2,分别对应目标转速n1和实际转速均值n2,隐含层为8,输出层为3,分别对应ΔKp,ΔKi和ΔKd[16]。 基于2.1节分析可知,BP-PID控制输出控制量为: u(k)=u(k-1)+ΔKp×[e(k)-e(k-1)]+ΔKi×e(k)+ΔKd×[e(k)-2e(k-1)+e(k-2))] (12) 式中,e(k) —— 当前期望输出与实际输出之差 u(k) —— 当前控制量 根据图1单轨吊起吊液压系统原理建立如图5所示仿真模型。本研究以某单轨吊起吊系统为仿真对象,在典型工况下进行仿真,即:偏载起吊、起吊过程负载突变、以不同的起吊速度进行起吊。忽略系统泄漏,根据某单轨吊起吊系统设置元件参数如表1所示。 表1 仿真参数Tab.1 Simulation parameters 图5 AMESim仿真模型 在AMESim中建立联合仿真接口,运行仿真打开MATLAB/Simulink,根据图4建立如图6所示仿真模型。本研究采用解析法初步整定PID初始参数为ΔKp=10,ΔKi=0.1,ΔKd=0.01,设定目标转速为150 r/min。 图6 同步控制器模型 如图7a所示,当目标转速为150 r/min时,系统采用PID控制的起吊马达1最大转速为182.5 r/min,起吊马达2最大转速为168.4 r/min,起吊马达1超调量为21.7%,起吊马达2超调量为18.9%;系统采用BP-PID控制的起吊马达1和2没有超调量。如图7b所示,系统采用PID控制的起吊马达最大同步误差为64.8 r/min,系统在1.12 s时达到稳定的目标转速;系统采用BP-PID控制的起吊马达最大同步误差为32.58 r/min,系统在0.55 s时达到稳定的目标转速,系统采用BP-PID控制相对于PID控制最大同步误差降低了49.7%,响应时间减少了50.9%。 图7 偏载启动同步曲线 综上所述,偏载启动时,系统采用BP-PID控制相对于PID控制,起吊马达1超调量降低了21.7%,起吊马达2超调量降低了18.9%,最大同步误差降低了49.7%,响应时间减少了50.9%。 为了测试系统的鲁棒性,在2 s时分别对起吊马达1和2进行负载突变,即工况1,一个起吊马达负载增加25 N·m,另一个起吊马达负载减小25 N·m;工况2,两个起吊马达负载同时增加25 N·m;工况3,两个起吊马达负载同时减小25 N·m。 如图8a所示,系统采用PID控制的起吊马达最大同步误差为16.5 r/min,系统在0.78 s时达到稳定的目标转速;系统采用BP-PID控制的起吊马达最大同步误差为8.5 r/min,系统在0.59 s时达到稳定的目标转速,系统采用BP-PID控制相对于PID控制最大同步误差降低了48.5%,响应时间减少了24.4%。如图8b所示,系统采用PID控制的起吊马达最大同步误差为11.5 r/min,系统在0.75 s时达到稳定的目标转速;系统采用BP-PID控制的起吊马达最大同步误差为8.4 r/min,系统在0.6 s时达到稳定的目标转速,系统采用BP-PID控制相对于PID控制最大同步误差降低了27%,响应时间减少了20%。如图8c所示,系统采用PID控制的起吊马达最大同步误差为9.5 r/min,系统在0.51 s后达到稳定的目标转速;系统采用BP-PID控制的起吊马达最大同步误差为8.5 r/min,系统在0.48 s时达到稳定的目标转速,系统采用BP-PID控制相对于PID控制最大同步误差降低了10.5%,响应时间降低了5.9%。 图8 抗负载突变同步曲线 综上所述,负载突变时,系统采用BP-PID控制相对于PID控制能够有效降低系统最大同步误差,减少系统响应时间,使系统具有更好的鲁棒性。 为了测试系统的调速性能,以4 s为一个仿真周期,分别设定改变目标值为依次为200, 250, 300, 250, 200, 150, 100 r/min。本研究主要详细分析目标转速由200 r/min增加到250 r/min,由250 r/min减速到200 r/min时的系统调速特性。 如图9a所示,当目标转速由200 r/min增加到250 r/min时,系统采用PID控制起吊马达1最大转速为256.5 r/min,起吊马达2最大转速为256.1 r/min,起吊马达1超调量为2.6%,起吊马达2超调量为2.4%。系统采用BP-PID控制起吊马达1最大转速为253.5 r/min,起吊马达2最大转速为250.5 r/min,起吊马达1超调量为1.4%,起吊马达2超调量为0.2%。如图9b所示,系统采用PID控制1.1 s后达到稳定转速,系统采用BP-PID控制0.85 s后达到稳定转速,系统响应时间减少了22.7%。如图9c所示,当目标转速由250 r/min减少到200 r/min时,系统采用PID控制起吊马达1最小转速为188.5 r/min,起吊马达2最小转速为193.5 r/min,起吊马达1超调量为5.8%,起吊马达2超调量为3.3%。系统采用BP-PID控制起吊马达1最小转速为198.5 r/min,起吊马达2最小转速为197.5 r/min,起吊马达1超调量为0.8%,起吊马达2超调量为1.25%。如图9d所示,系统采用PID控制0.98 s后达到稳定转速,系统采用BP-PID控制0.62 s后达到稳定转速,系统响应时间减少了36.7%。 图9 调速同步曲线 综上所述,系统采用BP-PID控制相对于PID控制,无论目标转速增加还是减少,都能有效降低系统超调量,降低系统响应时间。 分析单轨吊起吊液压系统原理,同时分析转速控制原理和同步控制策略,并设计BP-PID控制器。对系统进行建模和仿真,并与PID控制比较分析系统偏载启动特性、鲁棒性和调速特性,可以得到以下结论: (1) 当系统偏载启动时,系统采用BP-PID控制相对于PID控制, 起吊马达1超调量降低了21.7%, 起吊马达2超调量降低了18.9%,最大同步误差降低了49.7%,响应时间减少了50.9%; (2) 当负载突变时,系统采用BP-PID控制相对于PID控制能够有效降低系统最大同步误差,减少系统响应时间,使系统具有更好的鲁棒性; (3) 当系统调速时,系统采用BP-PID控制相对于PID控制,无论目标转速增加还是减少,都能有效降低系统超调量,降低系统响应时间; (4) 该系统能够有效提高单轨吊起吊系统面对偏载启动、负载突变和系统调速时的自适应性,为单轨吊智能化远程控制研究提供参考。1.3 同步控制策略分析
2 BP神经网络原理与BP-PID设计
2.1 BP神经网络原理
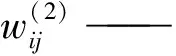
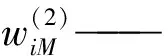
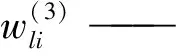
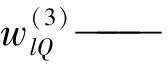
2.2 BP-PID设计
3 系统建模
3.1 液压系统建模
3.2 同步控制器建模
4 仿真结果分析
4.1 系统偏载启动特性分析
4.2 系统抗负载突变特性分析
4.3 系统调速特性分析
5 结论
