脂润滑弧齿锥齿轮热弹流润滑与效率研究

2024-04-11王振博

摩擦学学报 2024年3期

王振博, 郑鹏

(沈阳工业大学机械工程学院, 辽宁沈阳 110870)

弧齿锥齿轮的润滑状态对飞行器传动系统的可靠性和效率至关重要. 载人飞行器往往具有体积较大的冷却系统，而某些种类的无人机却没有. 近年来油动重载四旋翼无人机作为1种重要装备被各国重视，为了减重，移除齿轮箱冷却系统，同时考虑飞控问题使用润滑脂对弧齿锥齿轮进行润滑，因此设计人员必须准确了解齿面润滑状态. 这是1个新的挑战，随着油动重载旋翼机的兴起，高速重载脂润滑齿轮的润滑研究变得越来越重要.

很多学者在螺旋锥齿轮的浸油润滑研究领域进行深耕，为之后的研究者提供了丰富的研究方法及思路. 一些本领域的奠基人，诸如Dowson[1]和Cheng等[2-3]提出了热弹流相关理论，并给出了热影响的相关解释，其理论影响深远，至今仍被广泛使用. Pu和Zhu等[4]提出了1种用于弧齿锥齿轮和准双曲面齿轮齿面的摩擦系数和闪蒸温度的预测方法. 他们还研究了不同的卷吸速度方向对齿面摩擦系数和闪蒸温度分布的影响. Wang等[5]建立了弧齿锥齿轮瞬态热弹流模型，指出中心油膜厚度比平均油膜厚度更容易受到粗糙度的影响. Bobach等[6]采用了类似的方法，提出建立三维接触几何结构，并采用数值方法求解了同时考虑剪切稀化、非牛顿流体、混合润滑和微流体动力学条件的广义雷诺方程. Mohammadpour等[7]研究了准双曲面齿轮副的传动效率，用以提高车辆燃油效率并减少有害气体排放；他们将准双曲面齿轮置于混合非牛顿热弹流条件下，并指出热效应显著影响润滑油的性能. Wang等[8-9]强调了温度升高能够显著影响弧齿锥齿轮润滑状态，并开发了1种混合热弹流模型来预测一些参数，如油膜厚度、压力和温升. 以上工作均为油润滑弧齿锥齿轮的研究，但可以为脂润滑弧齿锥齿轮的研究提供了一些方法和评价标准.

油润滑弧齿锥齿轮的热弹流润滑状态已有广泛研究，但对脂润滑传动系统的热弹流润滑研究很少.近些年关于脂润滑的研究主要以试验研究为主，少数一些学者对表面形状简单、工况较为单一的零件进行了数值研究. Schultheiss等[10]在对脂润滑直齿轮的试验中发现，在不同的应力条件下，润滑脂的黏度对齿轮表面的润滑效果及磨损有很大影响. Zhang等[11]提出了脂润滑有限线接触的数值模型，并提出了1种预测油膜厚度和载荷比的简单方法. Zheng等[12]研究了润滑脂椭圆接触塑性弹流润滑(EHL)模型，发现当润滑脂具有高流变系数和剪切模量时，工作表面的最大残余应力和残余变形在重载条件下会有效降低. Fryza等[13]通过对脂润滑塑料零件的研究发现，润滑脂与其基础油油膜厚度之间的比率，受到负载和流体非牛顿响应的影响. Zhang等[14]在试验中发现，脂润滑时触点的接触状态十分关键，尤其是负载的变化，这一点与油润滑有较大区别. Mastrone等[15]提出了1种基于计算流体力学的有限元仿真方法，对脂润滑直齿轮进行了效率研究，但此种方法计算量较大，并且对复杂曲面建模的要求较高. 基于三脚架滑动万向联轴器，Zhou等[16]研究了润滑脂的热弹流特性，结果表明热效应显著影响润滑脂膜的形成. 由于润滑脂本身具有复杂性质，以及脂润滑弧齿锥齿轮应用的特殊性，目前关于脂润滑弧齿锥齿轮的混合热弹流相关问题未见文献有相关报道. 鉴于此，本研究中在假设齿面粗糙度符合正态分布的前提下，提出了1种润滑脂混合摩擦热弹流模型. 研究了弧齿锥齿轮齿面啮合接触路径下的润滑脂油膜厚度、摩擦系数和啮合效率. 分析了油动力重载无人机齿轮箱中弧齿锥齿轮的润滑状态，为高速重载脂润滑弧齿锥齿轮的润滑状态估计提供了参考.

1 齿面接触分析

对脂润滑弧齿锥齿轮进行热弹流特性及效率分析，首先需要求出齿轮啮合点处的几何参数、速度参数和载荷参数等重要参数. 生成齿轮齿面模型的方法有很多，其中最成熟的方法是通过模拟齿轮加工过程来获得齿面模型，Simon[17-18]对此进行了详细介绍. 所需参数可通过加载接触分析方法获得，这是1种用于检查齿面啮合质量的复杂技术. 由于弧齿锥齿轮齿面模型建立较为繁琐，以下直接给出所需参数的计算方法和相关参考文献. 为了描述弧齿锥齿轮齿面接触几何参数，需要建立与大齿轮和小齿轮固定连接的2个坐标系如图1(a)所示.

Fig. 1 Schematic diagram of gear coordinate system and contact area: (a) gear space coordinate; (b) vector diagram of the relative velocity vector; (c) vector diagram of tooth contact area; (d) vector diagram of entraining speed the sliding speed图1 齿轮坐标系及接触区域示意图：(a)齿轮坐标系；(b)相对运动矢量图；(c)接触区矢量图；(d)接触区内卷吸速度与滑动速度矢量

矢量Pr是大齿轮轴的单位矢量，Pl是小齿轮轴从圆锥底部指向锥顶的单位矢量.Jr和Jl分别是Pr和Pl的法向量，Or和Ol是齿坯的锥顶，也是装配时的交点. 根据图1(b)可知，卷吸速度矢量Ue和相对滑动速度矢量Us可表示为[19-21]

式中， ωl表示小齿轮的角速度，Ng和Np分别表示大齿轮和小齿轮的齿数，Rbr和Rbl分别表示坐标系 Σr和Σ1从锥顶指向接触点的方向矢量.

由于速度矢量的方向未知，仅由式(1)和式(2)给出的条件不足以计算滑动速度和卷吸速度.ua和ub是分别属于赫兹接触椭圆长轴和短轴的速度矢量.tr和tl分别是垂直于大齿轮齿面法向量nr和小齿轮齿面法向量nl的单位切向量. 根据图1(c)，表示为

式中， ∆τ为图1(c)中所示夹角.

根据图1(d)，Ue和Us可以沿着赫兹接触椭圆区域的长轴和短轴计算.

式中， θe为卷吸速度方向与椭圆短半轴夹角， θs为相对滑动速度与椭圆短半轴夹角.

弧齿锥齿轮接触区域的曲率是计算时所需的重要参数，这与弧齿锥齿轮加工调整参数有关. 为了能够确定共轭曲面接触椭圆主方向上的法曲率，需要计算沿小齿轮齿面t1(r)×n(1r)和t(1r)方向上的法曲率Kxl和Kyl，还有t(1r)×n(1r)方向上的扭曲率Gxl；大齿轮相对应的参数表示为Kxr、Kyr和Gxr. 根据图1(c)所示，接触椭圆参数可表示为[19-21]

式中，上角标 r 表示此向量为小齿轮坐标系 Σl内的向量在大齿轮坐标系 Σr中的表示形式. ∆τr为椭圆接触区域长半轴与向量tr×nr的夹角可表示为式(8).

根据共轭原理，相对法曲率的极值方向即为主方向，也就是椭圆接触区域的长半轴与短半轴方向. 那么对相对法曲率求极值就可以得到大齿轮和小齿轮的长、短半轴主法曲率Kar和Kbr以及Kal和Kbl.

2 考虑卷吸速度方向和粗糙度的脂润滑混合热弹流模型

润滑脂由增稠剂和基础油构成，其黏度对温度比较敏感. 由于无人机齿轮在巡航高速运转时，齿面对润滑脂的剪切力大于润滑脂的极限剪切应力，所以在这种工作条件下常常表现为非牛顿流体[22-23].

2.1 雷诺方程推导

描述润滑脂的本构方程常用的有3个.

式中，τ 、τs和η分别代表剪切应力、剪切屈服应力和润滑脂黏度；n为流变系数.是剪切率，其可以表示为油膜厚度方向上的速度梯度=du/dz，其中u代表两表面间的相对滑动速度，z代表两表面间的距离.Herschel-Bulkley模型在润滑脂低速剪切时有着较高的准确度[24]，一旦剪切力超过了润滑脂的剪切屈服应力极限 τs，那么Herschel-Bulkley模型与Ostwald便再无区别[25]. 由于齿面非光滑，推导过程考虑了Patir等[26]和Pei等[27]提出的压力流量系数.

以x方向为例，y方向同理，考虑微元平衡条件可得

式中，p为流体所受压力， τ为Ostwald模型所表示的剪切应力，将式(13)化简可得

将本构方程Ostwald模型代入式(14)得到

式中， η为润滑剂黏度，n为流变系数. 对z进行积分，边界条件给为可得

式中，h为两表面间的油膜厚度. 在高速重载条件下的弧齿锥齿轮，只需计算剪切流，形式如式(17)所示.

式中，hp为剪切流油膜厚度，he为2个相对运动齿面间的距离. 对式(17)进行积分，并考虑文献[26]中描述的流量系数 ϕx，可以得到考虑流量系数的剪切流方程为

式中，h=he-hp；根据连续流动性条件，即流入流体质量等于流出流体质量，那么

式中，mx是x方向上的质量流，my是y方向上的质量流， ρ为润滑脂的密度，Uh和U0分别表示微元的上下表面速度. 将(19)式化简后可得到

式中，p为流体动力压力，h为名义油膜厚度， ϕUscos(θs)和ϕUssin(θs)分别为沿相对滑动速分量的压力流动系数. 需要注意的是，对式(19)进行整理时应当注意Uh和U0分别表示流体微元上表面和下表面的速度，而其过程中的(Uh-U0)dxdy项往往被表示为如果使用稳态模型那么可以去掉式(20)中的项.

式中， σ为表面粗糙度高度的标准差.

2.2 考虑温度影响的黏压方程与密压方程

润滑脂的黏度与密度受温度的影响变化较润滑油大得多，所以在进行润滑分析时不能忽略温度的影响，下面给出考虑温度影响的黏压方程与密压方程[28].

式中，p0、 η0、 ρ0和T0分别为初始油膜压力、黏度、密度和温度.p和T分别表示当前计算压力和温度值.z为黏压系数，一般表示成z=α/[5.1×10-9×(lnη0+9.67)]，α为基础油的Barus压力黏度系数.

2.3 粗糙度条件下的膜厚方程

式中，δg和 δp分别为2齿面上各自的粗糙度分布矩阵，H0为刚体中心油膜厚度，Rx和Ry分别代表两齿面接触椭圆x和y方向的综合曲率半径，E′为当量弹性模量，pt(x∗,y∗)代表流体与微凸体承担压力的总和.

2.4 考虑微凸体接触的载荷平衡方程

式中，W代表总载荷，pc为微凸体压力，p为流体压力，pt为接触面积上的总压力. 其中微凸体压力pc采用K-E模型计算，详情请参考文献[29]，其形式如下：

式中，Fc为微凸体承载的载荷，Ac为微凸体接触面积，R未微凸体半径， ϕ(z)为粗糙度峰高度分布函数，K为硬度系数， υ为泊松比，hd为齿面材料硬度， ωc为弹性变形与塑性变形的临界值干涉值，h0代表含粗糙度在内的两表面分离值，N0为发生接触的微凸体数目.

2.5 考虑混合摩擦的能量方程

式中，cp为润滑脂比热容； ρ为润滑脂密度；k代表导热系数； η为润滑脂黏度；u、v和ω 分别代表x、y和z方向上的速度； τc= µpt为复合摩擦剪应力，如果不考虑摩擦力，则移除右端的第4项， µ为复合摩擦系数.

3 摩擦系数估计

润滑脂具有剪切稀化的特质，即剪切速率越高剪切力越大，润滑脂表现的黏度越低[28]. 但是油膜每层之间能传递的剪切力是有限的，根据文献[30]中的描述，采用Ostwald本构方程估计的润滑脂剪切摩擦力结果大于实际的剪切摩擦力. 为了使结果更加接近实际情况，采用非牛顿流体本构方程来近似计算润滑脂在高速剪切条件下的剪切力. 使用B-W模型，形式如下：

式中， τlim代表极限剪切力， τf代表实际剪切力， γl代表压力系数， βl是温度系数， τ0一般取值在1~8 MPa ，γl在0.03~0.15间取值，详情参考文献[31].

考虑混合摩擦的齿面摩擦系数可以表示为

式中， µc为齿面接触干摩擦系数，W为齿面载荷.

4 混合摩擦下的传动效率

排除振动等其他因素，齿轮最大的效率损失由啮合位置处的相对滑动摩擦引起. 滑动摩擦力(Fs)一般用式(28)计算.

由于弧齿锥齿轮齿面较为复杂，文献[30,32]指出，可以采用线接触润滑模型来近似滚动摩擦力(Fr)，表示为

式中，G=αE′为无量纲材料参数，αU=η0Uecosθe/(E′Rx) ，为无量纲卷吸速度， αW=W/(αE′Rx)，为无量纲载荷.

Xu等[30]指出，由于弧齿锥齿轮齿面相对滑动速度较大，摩擦热会对滚动摩擦系数有影响，所以采用热影响因数 φT来减小误差，那么

式中，Fr为滚动摩擦牵引力，Fr1为考虑热影响后的修正摩擦牵引力，ph为流体动力压力，E′为当量弹性模量， S RR 为滑滚比，Vs为两表面相对滑动速度，Kf为润滑剂的热传导系数.

当只考虑摩擦损失时，瞬时传动效率( ηe)表示为

式中，Tg为大齿轮的转矩， ωg为大齿轮的转速.

5 数值方法与结果分析

5.1 数值方法

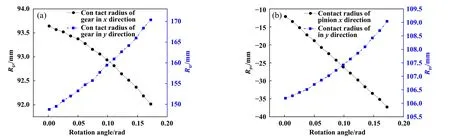
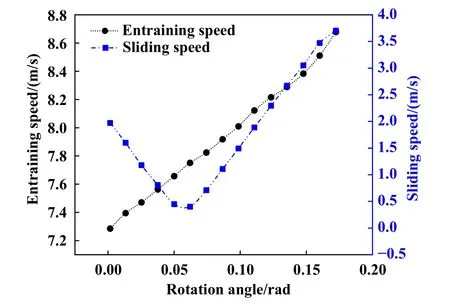
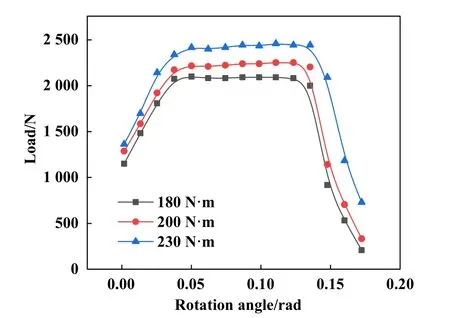
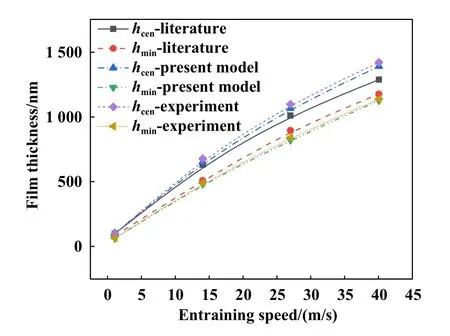
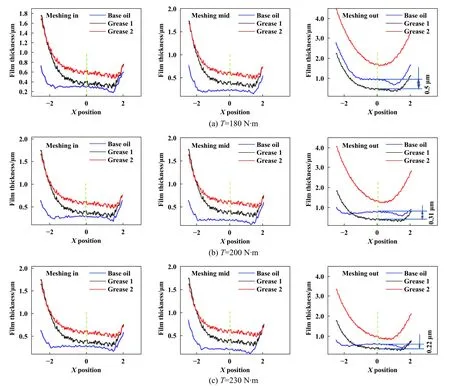
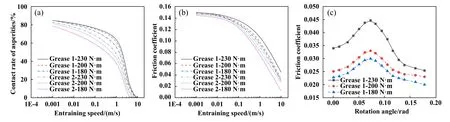
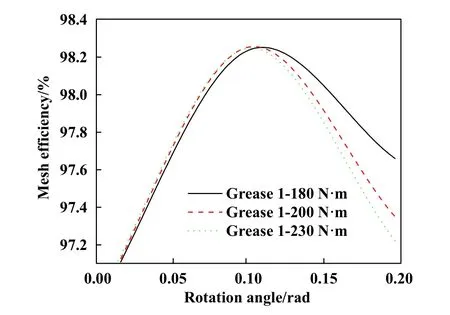
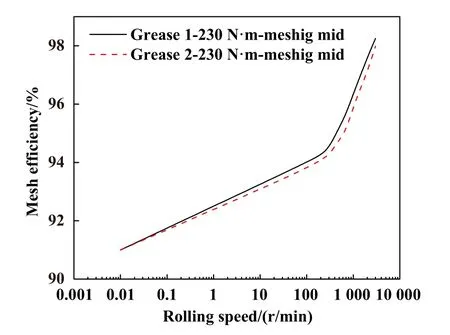
采用有限差分法求解了雷诺方程，并假设迭代初始流体压力为赫兹接触应力. 求解区域为2.5

Fig. 2 Flow chart of Reynolds equation solution图2 雷诺方程求解流程图

5.2 结果与分析

以四旋翼油动重载无人机的弧齿锥齿轮作为研究对象，研究了其润滑状态及效率问题. 2齿轮均由相同材料制成，其弹性模量为211.11 GPa，泊松比为0.3.齿轮表面粗糙度采用高斯分布函数进行模拟[34]，粗糙度半径设为0.2 μm，复合均方根粗糙度根据齿轮制造精度设为0.3 μm. 齿轮的基本参数列于表1中，润滑脂及其基础油的相关参数列于表2中.

表1 齿轮相关参数Table 1 Relevant parameters of gear

表2 润滑脂参数Table 2 Grease parameters

根据式(7~9)分别求得了大齿轮和小齿轮齿面啮合时在x方向和y方向上的接触半径. 如图3所示，Rgx和Rgy分别代表大齿轮齿面上沿x方向和y方向上的接触半径，Rpx和Rpy分别代表小齿轮齿面上沿x方向和y方向上的接触半径，其中图3(a)中为大齿轮参数，图3(b)中为小齿轮参数.

Fig. 3 Contact radius of tooth surface: (a) gear; (b) pinion图3 齿面接触半径：(a) 大齿轮；(b) 小齿轮

根据弧齿锥齿轮齿面接触模型，使用公式(1~6)计算了齿轮在3 000 r/min时的齿面卷吸速度和相对滑动速度，其结果如图4所示.

Fig. 4 Entraining speed and relative sliding speed图4 卷吸速度与相对滑动速度

由图4可知，在1个啮合周期内，卷吸速度从啮入点到啮出点是单调递增的，而相对滑动速度是先减小后增大，相对滑动速度最低的点也就是节点. 巡航工作状态占无人机总工况的90%以上，在巡航工作状态中，无人机的动作都是由改变螺旋桨桨叶的角度来完成的. 这里给出转矩分别为180 (稳定巡航)、200 (缓慢爬升)和230 N·m (巡航规避)的3种情况. 弧齿锥齿轮工作时会有多个轮齿同时参与啮合，根据文献[30]中提出的方法计算了1个啮合周期内的单齿载荷情况，当齿轮转矩分别为180、200和230 N·m时，1个啮合周期内轮齿从啮入至啮出过程中齿面接触点承载载荷与齿轮旋转角度之间的关系如图5所示. 不难看出，随着转矩的增加，齿面接触点载荷也随之增加.

Fig. 5 Relationship between load and gear rotation angle图5 承载载荷与齿轮旋转角度之间的关系

从式(10~20)推导了考虑粗糙度的润滑脂雷诺方程，为了证明模型的有效性，采用文献对比的方法来证明. Zheng等[12]建立了润滑脂塑性动压润滑模型，并在其论文中通过油膜中心厚度和最小油膜厚度作为度量与试验进行对照. 本文中模型代入文献[12]中的相关参数，计算了中心油膜厚度和最小油膜厚度，并与文献中的试验结果进行了对比，结果如图6所示.

Fig. 6 Model validation图6 模型验证

从整体看，在0~40 m/s的卷吸速度区间内，本文中模型对试验结果的拟合度高于文献中数值模型. 与文献中数值模型相比较，在0~4 m/s卷吸速度区间内区别不明显，但是数值结果在中速及高速区出现了较大不同，其膜厚最大差距为44.335 n m. 相比较于试验结果，文献中的模型与本模型在高速区的表现差距明显，本文中模型更贴近于试验结果. 这是由于润滑脂的塑性流体性质在低速剪切时可以保持，然而润滑脂并不是完全理论上的塑性流体，当其遭受高压高温的环境时，还表现出一部分弹性流体性质. 在高速剪切阶段，由于剪切热的存在，润滑脂将以高黏度油的性质参与润滑. 由图4可知齿轮组卷吸速度在7.2~8.7 m/s之间，图6表明在此速度区间内本文中的数值模型结果与试验结果吻合度较高，能够较为准确地描述真实油膜厚度，证明此模型适用于本文中的问题研究.

图7所示为在不同的转矩T(180、200和230 N·m)条件下，使用不同的润滑剂(基础润滑油、润滑脂1和润滑脂2)时，齿面所选取的3个啮合位置[啮入点(meshing in)、啮合中点(节点(meshing mid)和啮出点(meshing out)]处的油膜厚度变化情况. 由于在齿面接触区域内粗糙度峰值的分布是随机的，因此局部的油膜厚度不能完全反映润滑状态. 为了便于观察，图7所示为椭圆接触区域沿X轴向Y方向投影的油膜厚度平均值. 从整体来看，油膜厚度随着扭矩的增加而减小，黏度高的润滑剂所形成的油膜较厚. 在啮入点处，采用润滑脂1和基础润滑油的中心油膜厚度较为接近，在扭矩较低时更明显. 在节点处3种润滑剂的油膜厚度有明显区别，而实际上，润滑脂1和润滑脂2的油膜厚度变化较小，而基础润滑油的油膜厚度下降较大. 这是由于基础润滑油黏度较低流动性好，在较大压力下，会在更大的范围内形成动压油膜并降低油膜厚度. 在啮出点处，由于卷吸速度很大，3种润滑剂的油膜厚度都有了明显提升. 仔细观察发现，此时的基础润滑油油膜厚度已经超越了润滑脂1的油膜厚度；随着扭矩的增大，基础润滑油和润滑脂1的中心油膜厚度又开始靠近，这是由2种流体不同的特性所决定的，润滑油在计算中被假设为理想的黏弹性流体，而润滑脂为带有塑性流体性质的非牛顿流体；当卷吸速度较大时，润滑油被大量带入润滑区域，油膜的厚度会快速增大，而润滑脂由于其具有塑性性质，流动性不及润滑油，油膜厚度增加程度较小；而同样由于流动性的缘故，在相同的压力增加值下，润滑油的油膜厚度下降数值要明显大于润滑脂油膜，这就导致基础油油膜厚度先超过润滑脂1后，随着扭矩的增加油膜厚度差距减小的现象. 这说明在适当的条件下，一定黏度的润滑脂中心油膜厚度和基础油中心油膜厚度较为相似. 同时不难看出，在啮入点处一些润滑剂的油膜厚度有低于粗糙度平均峰值0.3 μm的现象，而啮出点处油膜厚度都大于0.3 μm. 这能够反映出一定工况条件下，在1个啮合周期内齿面的润滑状态是有可能发生变化的.

Fig. 7 Comparison of film thickness图7 油膜厚度对比

Li等[35]在润滑脂弹流润滑的球盘试验研究中发现，在一定的速度和载荷下，润滑脂的中心油膜厚度与其基础油的中心油膜厚度高度相似. 有一些学者提出可以在高速剪切条件下用润滑油的膜厚公式来近似润滑脂的膜厚[36-37]. 然而在弧齿锥齿轮的齿面上，在节点和啮出点处可以看出，基础油与润滑脂的油膜中心厚度有明显的区别. 这是由于在球盘试验中，接触半径、载荷和卷吸速度等都不在短期内发生剧烈变化，并且可以做到一直保持润滑脂剪切稀化的条件.然而在弧齿锥齿轮的齿面上，虽然转速可以保持不变，但从啮入点到啮出点的过程中，接触半径、载荷和卷吸速度等都发生较大的变化. 也就是说，在1个啮合周期内，轻负荷和重负荷以及高剪切速率和低剪切速率可能同时发生. 因此在估计脂润滑弧齿锥齿轮的润滑状态时应谨慎选择估计方法.

为了研究齿轮在不同转速下的效率损失规律，图8所示为微凸体载荷率和摩擦系数的计算结果. 图8(a)所示为节点处的载荷率随卷吸速度的变化；图8(b)所示为节点处摩擦系数随卷吸速度的变化；图8(c)所示为在转速为3 000 r/min时，1个啮合周期内齿面摩擦系数的变化规律. 由文献[38]给出的评判标准可知，若微凸体载荷率在85%以上时可定义为边界摩擦，载荷率为0%时进入全膜润滑状态，而这之间的状态即是混合润滑. 摩擦系数同样与微凸体载荷率相关，当齿面不在全膜润滑状态时，摩擦系数的值有干摩擦的贡献.观察图8(a)可知，相同卷吸速度下，润滑脂黏度越高，微凸体载荷率越低，转矩越大，微凸体载荷率越高. 润滑脂的黏度对摩擦系数的数值有较大影响，从图8(b)可以看出，高黏度的润滑脂虽然能提升油膜厚度降低载荷率，但是润滑脂本身的剪切力较大，低黏度润滑脂更能有效降低摩擦系数. 从图8(c)可以看出，1个啮合周期内的摩擦系数是时变的，因为在1个啮合周期内，齿面的接触半径、卷吸速度和相对滑动速度等都是变化的，而这些变化可以引起润滑脂性质较大的改变. 因此以往采用Benedic经验公式来估计齿轮效率的方法在脂润滑弧齿锥齿轮上要慎重使用[39].

Fig. 8 Load rate and friction coefficient: (a) variation of contact rate of asperities with suction speed; (b) variation of friction coefficient with entraining speed; (c) variation of friction coefficient at the meshing point of the tooth surface within one meshing cycle图8 载荷率与摩擦系数: (a)微凸体接触率随卷吸速度的变化; (b)摩擦系数随卷吸速度的变化;(c) 1个啮合周期内齿面啮合点处摩擦系数的变化

轮齿在1个啮合周期内的效率变化情况如图9所示. 可见，在润滑剂相同但转矩不同的条件下，1个啮合周期内的啮合效率是不同的. 在啮入点处效率最低，此处摩擦力由润滑脂剪切力和微凸体摩擦力组成而且受扭矩影响最小. 随着齿轮转角的增大，相对滑动速度在节点处大幅降低，微凸体摩擦损失减小，啮合效率提升. 在啮出点处可以看出，扭矩越小，啮合效率越高，可以说扭矩越小，啮合效率损失越小. 这是由于在啮出点处，齿面几乎处于全膜润滑状态，啮合效率的损失几乎全部来自于对润滑脂的剪切和挤压. 剪切率与相对滑动速度有关，挤压与载荷有关，二者的耦合造成了这种现象. 注意的是，虽然啮出点处几乎处于全膜润滑状态，但是其相对滑动速度最大，对润滑脂的剪切损失较大. 由于重合度的原因，啮出点处承载载荷最小，所以效率损失变化较大. 由此可知，在齿轮设计时应尽量减小啮出点处的相对滑动速度以及载荷来降低啮合效率损失.

Fig. 9 Meshing efficiency in a meshing cycle图9 1个啮合周期内的啮合效率

图10所示为润滑脂黏度不同的情况下，齿面节点处效率随转速的变化情况. 不难看出，低黏度的润滑脂能够有效减小啮合效率损失. 这是因为黏度高的润滑脂需要的剪切应力大，从而浪费了动力源的动力.在低转速区二者啮合效率区别较小，随着转速的增高，使用2种不同润滑脂的齿轮啮合效率都将增大；随着转速的增加区别逐渐增大，在接近3 000 r/min时差别又逐渐变小. 这是由于在极低转速区润滑脂剪切速率低，其塑性流体的性质较强，啮合时啮合效率损失较大，从而造成啮合效率较低；同时齿面相对滑动速度较低，使得两者之间的差别不明显. 随着转速增加，黏度较低的润滑脂较先开始发生剪切稀化，此时二者的啮合效率差距变得较为明显，随着转速不断提高，黏度高的润滑脂也开始有剪切稀化反应，二者之间的差距开始缩小.