轴承钢滚动接触疲劳亚表面夹杂处损伤分析

陈金华, 李淑欣*, 鲁思渊, 曹 均, 金永生

(1. 宁波大学 机械工程与力学学院 教育部冲击与安全工程重点实验室, 浙江 宁波 315211;2. 浙江省零件轧制成形技术研究重点实验室, 浙江 宁波 315211;3. 宁波银球科技股份有限公司, 浙江 宁波 315207)

轴承在接触疲劳载荷下的失效，除了表面脱落外，在亚表面会因微观组织变化而产生潜在的损伤.其中最典型的是在距离表面1 mm以内的局部区域，形成1种白色蚀刻组织(White etching area，WEA)，其因在光镜下呈现白亮色(马氏体轴承钢为黑色)而得名. WEA是塑性变形高度局域化的窄带，其宽度在3~80 μm之间[1-2]. 无论是国产的还是国外知名轴承公司生产的轴承钢，也不管是普通的热处理还是碳氮共渗的处理，都不可避免地出现该问题，这说明WEA损伤是马氏体轴承钢在接触疲劳载荷下的共性. 国内外学者对此进行了大量的研究，在微观组织及外载荷条件等方面有了较深的认识，但由于其特征形貌、诱发因素和形成机理非常复杂，WEA的形成过程仍存在很大的分歧.

接触疲劳载荷下，尽管轴承没有宏观的塑性变形，但其微观组织发生了严重的塑性变形. 在扫描电镜下观察到WEA处的马氏体和渗碳体被明显拉长，塑性变形高度局域化，呈现出变形带的特征. 2个相互接触的表面，最大剪应力和最大Mises应力发生在距离接触表面0.75b(b为接触宽度)处[3]. 而亚表面的非金属夹杂处由于高的应力集中常成为WEA的诱发地，对接触疲劳寿命产生很大影响[4]，其中亚表面的显微组织退化和裂纹生长是诱发滚动接触疲劳的两大影响因素[5-8]. 夹杂物两侧的WEA区域呈现出不同的形状和形貌，其中典型的是蝴蝶状(称为蝶形WEA). 国内外学者对WEA的形成进行了大量研究，如关健等[9-10]通过建立模型得出接触区域的正应力和剪应力分布，计算得出最大交变剪应力值约为0.5Pmax(Pmax为最大接触应力)，剪应力方向与滚道接触面呈45°夹角.Moghaddam等[11-12]建立了含夹杂物的二维和三维有限元模型，基于连续损伤力学研究了夹杂周围蝴蝶状的疲劳损伤. 损伤由剪切应力和平均剪应力决定，夹杂物周围存在4个最大交替剪切应力区域，可形成不同方向的WEA，但大多数蝶形WEA只有2个翅膀. 往复循环的剪切应力相比于平均剪应力是蝴蝶形成的主要驱动因素. Leroux等[13]和Koumi等[14]提出赫兹接触压力的改变会影响交变剪切应力与平均剪应力，与Moghaddam所提出的有限元模型(FEM)模拟相比，该模型考虑了材料损伤与夹杂物深度对赫兹接触压力的影响. 更好的解释了交变剪切应力相对于平均剪应力对白色蚀刻区扩展方向(即蝴蝶翅膀方向)影响更大. Alley等[15]研究了非金属夹杂物周围的塑性应变累积，认为WEA是由于局部剪切变形造成的塑性应变累积的结果. Wang等[16]基于晶体塑性有限元模型，并结合Fatemi-Socie多轴疲劳损伤准则，研究了夹杂物周围的疲劳损伤和棘轮损伤的形成和发展. 相比疲劳损伤，棘轮损伤始终占主导，且与轧制方向形成45°夹角.随着循环次数的增加，并受到微观组织各向异性的影响，棘轮损伤在晶界处形成. Cerullo和Tvergaard[17]基于Dang-Van准则研究了球形与立方形夹杂物对疲劳寿命的影响. 球形夹杂物相对于立方形夹杂物具有更高的损伤因子，在弹流接触应力下都会形成较大损伤因子的区域，与轧制方向成45°夹角. 在赫兹接触载荷下，损伤因子呈对称分布. 上述模型虽然体现了剪切应力是决定损伤区域方向的原因，也说明了微观组织变化是塑性变形累积主要影响因素. 但是模型并没有考虑材料软化，即未将损伤与数值模型耦合.

另外，WEA损伤的形状分布特征有很大的分散性. 作者前期的研究发现[18-19]，WEA只在某些特定的方位形成，且同1个试样的不同横截面上，既有变形程度相对较小的WEA (马氏体和渗碳体被显著拉长形貌)，又有变形严重局域化的WEA (形成高度致密的窄带，马氏体和渗碳体完全消失). 这说明相比于接触疲劳宏观有限元模型，微观组织结构变化才是影响WEA形成的重要因素，如晶体取向. 目前的模型和机理不能很好地解释该现象. 因此，合理的接触疲劳模型应在基于物质、能量和热力学守恒的前提下，由塑性变形功驱动，且考虑晶体取向的影响. 为此，本文中建立了接触疲劳载荷下的塑性损伤方程，并结合晶体塑性模型来研究夹杂处的应变局域化和塑性应变累积. 将模拟的结果与接触疲劳试验结果进行比较，讨论WEA的形成机制和影响其形貌的关键因素.

1 试验与有限元建模

1.1 滚动接触疲劳试验

本文中材料为国产轴承钢AISI 52100，其化学成分如下(质量分数，ω)：ω(C)=0.90%；ω(Cr)=1.87%；ω(Si)=0.31%；ω(Mn)=0.32%；ω(P)≤ 0.027%；ω(S)≤ 0.020%；其余成分均为Fe. 试样为上下接触的2个圆柱试样，由原始棒料根据YB-T5345-2006设计加工为圆环状，外径和内径分别为60和30 mm，厚度为20 mm，如图1所示. 试样在860 ℃下奥氏体化2 h，然后在油中淬火至室温. 并在160 ℃下回火1 h. 最终得到的显微组织为马氏体、碳化物和残余奥氏体，其体积分数小于5%.试样的平均硬度为58~60 HRC[2,19].

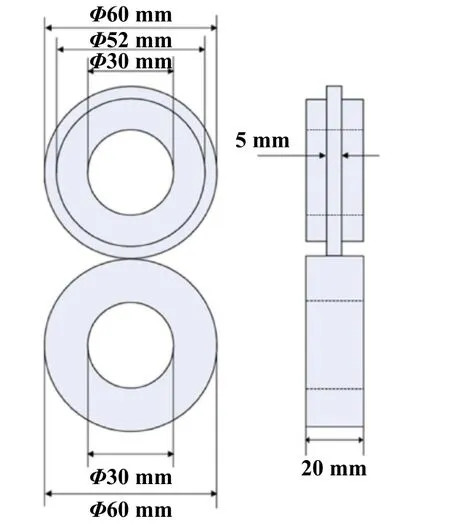
Fig. 1 Schematic diagram of sample size图1 试样尺寸示意图

试验采用MJP-30型滚动接触疲劳试验机，主要由主机、润滑系统、控制柜及计算机等部分组成. 通过液压油缸拉动上主轴座施加轴向拉力，将恒定的径向载荷施加于试样上. 2个试样由各自的电机驱动，可通过调节转速实现不同滚滑比[20]的接触疲劳. 对试样施加径向载荷，接触载荷为 2.6 GPa时，滚滑比为5%. 当表面出现宏观凹坑时，试样失效，机器停止运转，具体的试验过程参见文献[2]. 试验结束后，选取需观测的接触面区域(存在明显的失效形貌，如点蚀、剥落坑等)，利用电火花线切割机沿失效试样的周向及轴向将其切割至合适尺寸. 为了对亚表面微观组织的观察，需要对切割后的试样进行研磨、抛光并用体积分数为2%的硝酸酒精溶液腐蚀. 并利用扫描电子显微镜(SEM)和透射电镜(TEM)对WEA的微观结构进行观察，且使用电子背散射衍射(EBSD)测试揭示晶粒的取向分布.

为了获取模拟过程中需要的材料参数，利用纳米压痕试验所获取的载荷-位移曲线进行拟合. 样品表面用砂纸打磨，然后用颗粒直径为1.5和0.5 μm金刚石抛光至镜面. 为了达到纳米压痕试验和EBSD检测所需的表面质量，在25 ℃和电压30 V下，用体积分数为5%的高氯酸酒精溶液对样品进行电抛光240 s. 纳米压痕试验在海思创TI premier型纳米压痕仪中进行，在室温下使用金刚石三棱锥压头，设定载荷为5 000 μN，加载和卸载的时间均为15 s.

1.2 有限元建模

通过有限元软件ABAQUS建立了1个尺寸为100 μm×50 μm的矩形模型，表征为局部微观的单晶模型，如图2所示. 由于在椭圆形非金属夹杂物上可以观察到很多蝶形WEA[21]，因此在模型中插入了1个椭圆形夹杂物，夹杂物处于模型中间且与水平面成45°夹角. 轴承钢的弹性模量(E)为206 GPa，泊松比(v)为0.3；MnS和Al2O3是轴承钢常见的夹杂物，其弹性模量和泊松比分别为103 GPa、0.3和387 GPa、0.25[22-23]. 该夹杂物为软夹杂，其弹性模量(E)为20 000 MPa，泊松比(v)为0.3. 夹杂物弹性模量的影响将在下一节讨论. 椭圆的长轴和短轴分别为10和5 μm. 为与滚动接触疲劳(RCF)试验的边界条件一致，模型底端的自由度在y方向受到限制，x方向自由度在两侧都受到限制. 研究滚动接触疲劳塑性应变累积导致的应变局域化，需要模拟滚子在内滚道上循环滚动的运动过程. 如图2所示，用子程序DLOAD和UTRACLOAD将表面压力(Pmax=2.6 GPa)分布载荷和摩擦力施加在模型表面来模拟整个滚动过程. RCF模型由24 955个单元(CPE4T)组成，分析步为Coupled temp-displacement，网格尺寸均匀划分，每个单元的尺寸为0.5 μm×0.5 μm.

Fig. 2 The model of RCF图2 RCF模型

2 基于晶体塑性-相场模型夹杂处的损伤

基于传统晶体塑性流动准则[24-26]，并考虑滚动接触疲劳循环加载下的包辛格效应和材料损伤，本文中采用耦合各向同性硬化、非线性随动硬化准则和相场损伤的幂率模型来描述晶体的滑移剪切应变率.

根据Armstrong-Frederick型非线性运动硬化准则，各滑移系统背应力增量变化率的演化方程如下：

式中，c和b是材料硬化参数.α滑移系的各向同性硬化阻力的增量变化率表示为

式中，hαα和hαβ分别为滑移系的自硬化模量和潜硬化模量，n为滑移系个数，h0为初始硬化模量，τs为饱和剪切应力，τ0为初始临界剪应力，γ为总的滑移变形量，也叫累积剪切应变. 自硬化模量和潜在硬化模量满足以下关系：

式中，q为比例系数，一般取1，是自硬化系数与潜硬化系数的比值； δαβ为克罗内克函数，当 α=β 时， δαβ=1；当 α ≠β 时， δαβ=0.

根据非保守相场的Ginzburg-Landau模型[27]，相场损伤演化公式如下：

构建的赫尔姆霍兹自由能密度(HFED) ψ包含弹性应变能密度[28]ψe、塑性应变能密度 ψp与损伤界面能密度 ψc，如下式：

式中，ρ0为材料密度，t为时间，T表示第二P-K应力张量，Ee和Ep为格林弹性和塑性应变张量，其中塑性应变率为为α滑移系的剪切应变率，μ(α)为施密特因子，C为四阶弹性矩阵， ∇φ描述损伤梯度.ψG0和 ψH0分别是与和损伤界面扩散和损伤的能量阈值有关的参数，由ks和kg决定.m是相场势的阶数，G为表面能密度，lc是细观材料特征长度. 材料损伤退化公式D(φ) =φ2，0 ≤φ≤ 1，φ=1和φ=0分别表示无损和完全断裂的点.

根据热力学第二定律和熵不等式[28]可以将相场损伤演化公式表示为

式中， ρ为材料密度，c为比热容，k为热传导系数，Q为热量， θ为温度.

ABAQUS中的温度与位移耦合系统中的热传导方程，为抛物线型微分方程，如公式(12)所示. 本文中的相场损伤方程(11)也是抛物线型偏微分方程，2个方程形式一样. 因此在对塑性损伤耦合模型中的损伤进行有限元求解时，将温度用损伤代替，将抛物线型热传导微分方程替换成相场方程，这样可以直接采用软件中的模块. 这样的处理在文献中已采用过[29]. 晶体塑性损伤本构关系分别由用户子程序UMAT和HETVAL组成.

3 结果

3.1 WEA的形貌和组成

采用SEM观察试样接触亚表面区域，发现在距离接触表面650 μm的范围内，在非金属夹杂物上可以观察到不同形貌的WEA. 轴承钢中夹杂物主要成分是MnS或Al2O3[22-23]. 本文中试验用的轴承钢中主要是MnS，XRD检测结果如图3所示. Al2O3夹杂物在其他文献常有报道[30]. WEA的典型形貌照片如图4所示.图4(a)所示的夹杂物呈椭圆形，在夹杂物右侧形成蝶形WEA. 在WEA和基体之间的界面处存在裂纹，夹杂物左侧的裂缝与载荷滚动方向方向一致，裂纹一侧的显微组织略有变形. 图4(b)所示的WEA在夹杂物左侧形成，可以观察到少量未被溶解的碳化物组织，裂纹一侧的WEA明显地被剪切和拉长. 接触疲劳载荷下，尽管轴承没有宏观的塑性变形，但亚表面微观组织发生了严重的塑性变形. WEA处的马氏体和渗碳体被明显拉长，塑性变形高度局域化. 图4(c)和(d)是相应于图4(a)和(b)中TEM (白色圆圈内)明场照片. 可以看出，WEA中的晶粒被细化成纳米等轴晶，平均晶粒尺寸为10 nm (白色圆圈内). 即在塑性变形下，晶粒发生了塑性变形诱导的晶粒细化.

Fig. 3 EDS spectrum at inclusion图3 夹杂处的EDS谱

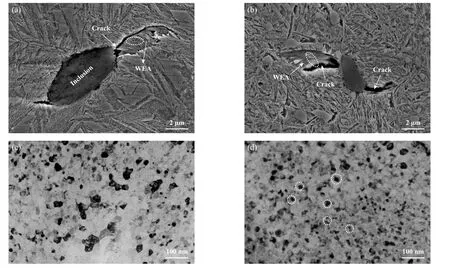
Fig. 4 SEM micrographs of different WEA morphologies at non-metallic inclusions: (a) WEA on the right side of the inclusion;(b) WEA on the left side of the inclusion; (c) and (d) TEM bright field micrographs of WEA corresponding to (a) and (b)图4 非金属夹杂物处不同的WEA形貌照片： (a)夹杂物右侧的WEA； (b)夹杂物左侧的WEA；(c)图(a)中WEA的TEM明场形貌照片；(d)图(b)中WEA的TEM明场形貌照片

3.2 材料参数标定

图5(a)所示为样品经过EBSD试验的取向映射图，可以观察到区域内晶粒的取向分布. 晶粒取向由欧拉角(φ1,Φ,φ2)表示，借助三维取向分布函数法(ODF)对晶粒取向的具体数值和强度进行准确标定，分别输出了φ2为0°、30°、35°和70°的ODF图，如图5(b)所示. 由于晶粒取向数目众多，本文中选择了3组强度较大的晶粒取向(A1、A2和A3)作为研究对象，3组欧拉角分别为(60°, 88°, 0°)、(75°, 60°, 35°)和(30°, 58°, 70°).

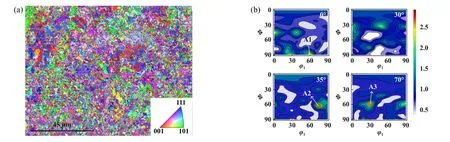
Fig. 5 (a) Orientation distribution of grains; (b) distribution of ODF图5 (a)晶粒取向分布图；(b)取向函数分布函数图

轴承钢AISI 52100为典型的体心立方结构(BCC)，含有48个滑移系，其中{110}<111>是BCC晶体的主要滑移系统. 在本文中，晶体中的位错滑移都发生在此滑移系统所包含的12个滑移系上. 轴承钢AISI 52100的显微组织由BCC结构的马氏体组织和渗碳体组成，但在纳米压痕模型与RCF模型中，只考虑马氏体相，在某些情况下，碳化物被视为造成应力增加的夹杂物[31].

晶体塑性本构方程的参数通过拟合纳米压痕试验提取的载荷-位移曲线获得，纳米压痕有限元模型尺寸为12 μm×12 μm×6 μm. 为保证压头不变形，将其设为离散刚性. 为获取准确的数据，在划分网格时，对模型表面到底部采用网格尺寸从小到大布种，并且与压头接触的区域得到了网格细化(单元尺寸为0.1 μm×0.1 μm)，如图6(a)所示. 假设接触表面没有摩擦，边界条件与试验一致. 在压头的尖端设置参考点，并在负y轴(压头剩余的自由度被完全约束)上施加191.7 nm(对应最大载荷)的位移. 需要指出的是，该模型采用的是基于传统塑性流动准则的本构模型，不考虑与相场损伤的耦合. 标定的初始参数(如弹性系数C11、C12和C44等)是根据文献[16]选择的. Han等[32]在拟合参数过程，发现不同晶粒取向下的拟合结果误差在12%左右，误差较小. 因此纳米压痕模型中选择强度较大的欧拉角(75°, 60°, 35°)，并利用试错法进行晶体塑性本构参数的拟合. 图6(a)所示为纳米压痕有限元模型的Mises应力云图. 该结果提取的载荷-位移曲线与图6(b)中纳米压痕试验提取的载荷-位移曲线有很好的一致性，表明材料参数是合理的. 晶体塑性本构相关参数列于表1中. WEA的宽度被限制为3~80 μm[21-33]. 为了模拟真实的WEA并减少计算时间，WEA宽度被设定为3 μm左右. 调整损伤方程参数M、ks和kg，直到RCF损伤模型中的损伤区域宽度达到3 μm (网格单元长度0.5 μm). 损伤方程的拟合参数列于表2中.

表1 晶体塑性本构模型材料参数(马氏体)Table 1 Material parameters (martensitic) of crystal plasticity constitutive model

表2 损伤方程参数Table 2 Damage equation parameters

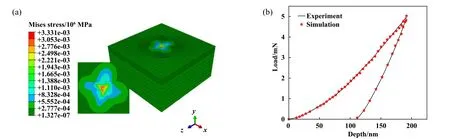
Fig. 6 (a) Nanoindentation finite element model-Mises stress; (b) load-displacement curve test and simulation fitting curve图6 (a)纳米压痕有限元模型-Mises应力云图；(b)载荷-位移曲线试验与仿真拟合曲线

4 讨论

4.1 不同晶体取向局部损伤形成

图7(a~f)所示分别为软夹杂处(弹性模量E=20000 MPa，泊松比υ= 0.3)对应欧拉角为(75°, 60°, 35°)的损伤云图和等效塑性应变(EPS)云图. 载荷加载前损伤参数为 φ 为1，随着塑性应变的增加趋于零. 损伤从夹杂物的两侧分别相对加载方向呈60°和230°的方向萌生和发展，前者的扩展速度远大于后者. 损伤逐渐发展成宽度为3 μm的变形带. 在随后的扩展中，损伤在带内进一步强化，变形带的宽度几乎没有变，最终成为高度局域化的变形带，如图7(c)所示. 损伤由应力集中诱发，夹杂处的应力由晶体塑性本构模型中的分解剪切应变决定，剪切应变越大，损伤越大. 应变能的不断累积导致应变局域化，从而形成损伤变形带，该变形带也叫剪切带(SB)[34]. 图7(d~f)所示为剪切带内塑性应变(EPS)的演化，塑性应变逐步增大的过程也是损伤不断累积和剪切高度局域化的过程. 带内中心处的剪切应变和损伤(根据式(11)，损伤φ越小，损伤越严重)最大，向带外两侧减小，如图7(g)所示.

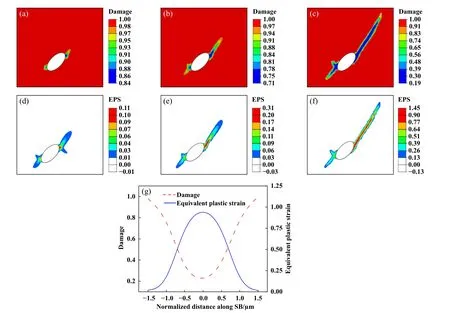
Fig. 7 (a~c) Damage contours at Euler angles (75°, 60°, 35°); (d~f) equivalent plastic strain contours;(g) damage and equivalent plastic strain with shear strip width change图7 (a~c)欧拉角(75°, 60°, 35°)时的损伤云图；(d~f)等效塑性应变云图；(g)损伤与等效塑性应变随剪切带宽度变化图

如前言所述，WEA是接触疲劳载荷下，夹杂处塑性应变累积局域化的结果，图7中的损伤分布和形貌照片与图4(a)和图4(b)中的WEA形貌照片和分布吻合. WEA中发生了大量的剪切塑性变形，微观组织明显被拉长. 根据大量的试验和现有文献的统计结果可知[1,18,21]，WEA中的局部微观应变在0.8~1.4之间，这与图7(f)剪切带中心处的最大应变值可达0.9的结果一致.

由于剪切带内变形高度局域化，对晶体取向具有很强的敏感性[35-36]，夹杂处晶体的不同取向导致不同的剪切带形貌和方位. 图8(a~c)和图8(d~f)分别为欧拉角为(60°, 88°, 0°)和(30°, 58°, 70°)的损伤. 与图7相比，损伤起始位置相同，但随后的发展路径却因晶体取向而改变. 图8(a~c)中的主剪切带沿着与载荷方向呈155°夹角的方向扩展，而另一侧的次剪切带则停止扩展，但图8(d~f)中的2个剪切带分别沿着与载荷方向呈55°和125°夹角方向同时扩展，该剪切带和图8(g)中WEA的扩展方向趋于一致. 将图7和图8中不同取向下剪切带中心处的塑性应变和损伤随着时间的变化进行对比，欧拉角为(75°, 60°, 35°)的塑性应变累积和损伤均大于其余2组取向，这是因为欧拉角(75°, 60°, 35°)的最大施密特因子均大于其余2组，如图9所示，这可以解释为什么不同形貌和方向的WEA会出现在同一个样品中.

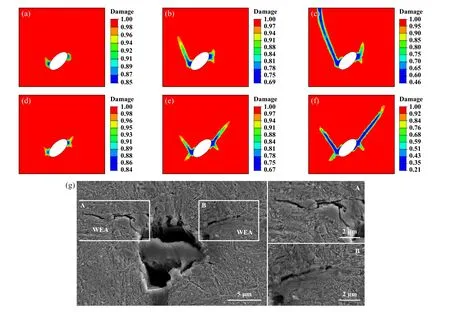
Fig. 8 Damage evolution of Euler angles for different crystal orientations: (a~c) (60°, 88°, 0°);(d~f) (30°, 58°, 70°); (g) SEM micrographs of WEA on both sides of the inclusion图8 不同晶体取向欧拉角的损伤演化：(a~c) (60°, 88°, 0°)；(d~f) (30°, 58°, 70°)；(g)夹杂处两侧WEA的SEM形貌照片

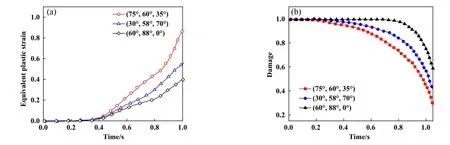
Fig. 9 The variation of damage and equivalent plastic strain with time under different orientations图9 不同取向下损伤与等效塑性应变随时间的变化

4.2 夹杂物弹性模量对剪切带形成的影响

塑性应变累积是损伤形成与发展的原因，而等效塑性应变与应力有关. 在目前关于WEA的研究中，统一将夹杂物归类为非金属夹杂物. Grabulov等[30]通过人工添加Al2O3，研究硬夹杂处的WEA，观察到夹杂两侧形成对称的蝴蝶状WEA. 然而，在没有非金属夹杂物的地方，也发现了大片的WEA，而这些WEA的形成很可能是碳化物作为硬相，对其局部应变局域化以及损伤的大小和分布产生较大影响[37].

图10所示为硬夹杂物处的Mises应力( σ)与最大接触载荷Pmax比值的分布，与计算塑性损伤的本构模型不同，该分布是根据线弹性本构计算的. 其中，硬夹杂的弹性模量E和泊松比υ分别为387 000 MPa和0.25[22].可以看出，软夹杂处应力集中的数值和范围均大于硬夹杂处的应力集中，前者应力集中数值为0.99，后者为0.82. 软夹杂处的应力集中来自左右两侧，如图10(a)中的嵌入图所示，随后在与加载方向成45°夹角的范围内发展. 如图10(b)所示，在硬夹杂物处，应力集中是从上下表面产生和发展的.

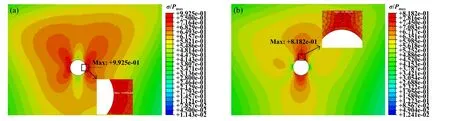
Fig. 10 Effect of different elastic modulus on stress distribution: (a) soft inclusions (E=20000 MPa);(b) hard inclusions (E=387000 MPa)图10 不同弹性模量对应力分布的影响：(a)软夹杂(E=20000 MPa)；(b)硬夹杂(E=387000 MPa)

与图7和图8中的软夹杂物(E=20000 MPa)相比，硬夹杂物处的损伤与夹杂物相切发展，如图11(a)中欧拉角(30°, 58°, 70°)的情况所示，形成了 “包围” 夹杂物的4个剪切变形带. 图11(b)所示为等效塑性应变的等值线分布，其大小沿变形带宽度的分布与软夹杂的趋势一样，中间高两侧低，最大塑性应变可达0.77. 无论是硬夹杂还是软夹杂，都呈现出剪切带中心塑性应变最大，损伤最大的现象. 且与图8中软夹杂处的剪切带与WEA形貌吻合相同，图11(a~b)中的剪切带形貌也与WEA形貌吻合，如图11(c)所示. 因此，不同硬度的夹杂物对WEA的影响仅仅是在WEA的萌生区域和扩展方向.

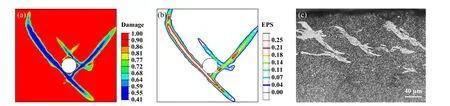
Fig. 11 (a) Damage contour, (b) equivalent plastic strain contour and (c) WEA of parallel strips[37]when Euler angles (30°, 58°, 70°)图11 欧拉角为(30°，58°，70°)时的 (a)损伤云图，(b)等效塑性应变云图以及(c)平行条带的WEA[37]

4.3 WEA中裂纹的形成

接触疲劳亚表面WEA形成机理的研究中，有相当一部分研究者认为裂纹是形成WEA的根源[38-40]. 理由如下：首先裂纹从夹杂处萌生，裂纹上下表面在疲劳载荷的作用下反复摩擦产生塑性变形，当塑性变形累积到一定程度后，微观组织发生变形诱导的晶粒细化.为了证明该机理，Paladugu等[41]采用特殊的热处理方法，得到晶界处含脆性裂纹的微观组织，之后进行接触疲劳试验，发现在晶界处产生大量伴随有裂纹的WEA. 然而，大量伴随裂纹的WEA只在裂纹的一侧产生，如图4(a)和(b)中WEA处的裂纹，其位于WEA与基体的界面处. 如果是因裂纹上下表面摩擦导致局部变形从而产生WEA，则WEA应该对称位于裂纹的两侧，而非一侧. 另外，该机制也无法解释在没有裂纹的地方发现了大量WEA的现象[1]. Kadin等[42]从理论上计算了裂纹摩擦所产生的塑性应变能，认为摩擦引起的热促使微观组织改变. 然而，试验中需要非常大的滑差率(300%)才能提供足够的能量使晶粒细化为纳米晶[43].由此可见，裂纹诱导WEA形成的机理存在很大争议，而理解该问题的关键是明确裂纹是在WEA形成之前还是之后产生. 为此，分析了剪切带中的应力分布.

图12(a~c)所示为欧拉角为(75°，60°，35°)时剪切带的应力演化云图，可以看出，随着剪切带的发展，带内应力逐渐衰减. 当应力趋于零的区域，就是微孔洞或者微裂纹产生的地方[44]. 随着应变的进一步增加，微孔洞密度增大，最终连成裂纹，导致WEA被裂纹分割，正如图12(d)所示，WEA内部存在许多微小裂纹(箭头标注处)将WEA分割. 图12(e)所示的应力和塑性应变随剪切带宽度的变化说明，剪切带内部处于低应力和高应变的状态. 需要注意的是，图12(e)中剪切带中心处的应力趋于零的情况是1种理想的情况，而实际中因剪切带内部微观组织的影响和变形不协调，会导致裂纹从带内其他地方萌生和扩展. 图4中的裂纹是在WEA与基体界面处产生的，图8(g)中既有界面处又有WEA内部的裂纹，甚至裂纹整个贯穿变形带，但这不影响裂纹和WEA形成的先后关系. 即接触疲劳载荷下，塑性变形高度局域化在3~80 μm的区域，导致剪切带WEA的形成；随着塑性变形局域化的增强，剪切带内塑性应变增大，但带内的应力下降，导致微裂纹萌生，并最终相互连接成为大的裂纹.

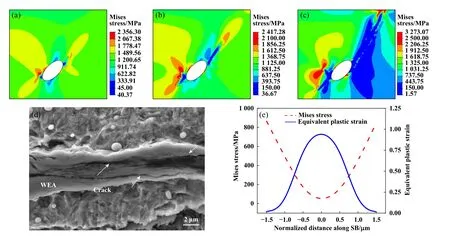
Fig. 12 (a~c) Variation process of Mises stress inside the shear zone; (d) crack in the middle of WEA;(e) variation of Mises stress and plastic strain along the width of the shear zone图12 (a~c) 剪切带内部Mises应力的变化过程; (d) WEA中间的裂纹; (e) Mises应力和塑性应变沿剪切带宽度的变化

5 结论

a. WEA本质上是剪切带，由塑性应变累积导致的剪切局域化而形成. 软夹杂物周围的剪切带和损伤的形成与蝶形WEA一致. WEA损伤的形貌和传播方向由晶体取向决定，即WEA的形成具有明显的晶体取向偏好，这很好地解释了为何在同一试样中观察到的WEA表现出不同形貌.

b. 与软夹杂周围的剪切带和损伤演化不同，硬夹杂处的剪切带与夹杂相切，形成的4条剪切变形带将夹杂 “包围” . 该剪切带的发展和试验中出现的大片WEA的形貌一致，为碳化物作为硬相对其周围应变局域化以及损伤大小和分布产生较大影响提供了合理的解释.

c. 剪切带内部处于高应变和低应力的状态，带中心处应变达到最大，随带宽两侧急剧减小，而中心处应力却最小，几乎为零，沿带宽两侧增大. 这说明裂纹在剪切带内萌生和扩展. 这阐明了裂纹和WEA形成关系的同时，也进一步说明WEA的形成机理是剪切局域化损伤的结果. 即裂纹是由WEA形成过程中剪切局域化不均匀造成，而非预先产生的裂纹表面相互摩擦导致WEA形成.