弹丸定心部-身管接触模型及其应用
2024-04-11钱林方
缪 伟, 尹 强, 钱林方,2
(1. 南京理工大学 机械工程学院, 南京 210094; 2. 西北机电工程研究所,陕西 咸阳 712099)
火炮发射时,弹丸定心部与炮膛之间存在间隙接触,该接触对身管有很大的激励作用;被激励的身管反过来影响弹丸在膛内的运动。定心部与炮膛的接触是弹炮耦合问题的一个重要组成部分。弹丸和身管之间的耦合作用是导致弹丸初始扰动的主要因素之一,对射击精度有强烈的影响。因此,研究弹丸定心部与炮膛的接触问题对于揭示弹丸的膛内运动规律、预测弹丸的炮口状态、提高火炮的射击精度具有重要的意义。
多体动力学接触建模的工作内容包括两部分:①接触体的几何描述和接触检测;②接触载荷的力学建模[1-2]。几何描述是为接触检测服务的。接触检测的目的是确定潜在接触区域的位置以及判断物体是否在接触区域内发生接触。在进行考虑弹管耦合作用的发射动力学分析时,一些文献中的工作是使用通用动力学软件(如Adams、RecurDyn、Prodas等)实现的[3-10]。通用动力学软件将物体表面离散成多边形网格,使用接触搜索算法找寻潜在接触区域并判断接触状态。接触计算过程非常耗时,通常占到问题求解时间的一半以上。当多边形面片只具有C0连续性并且接触面之间存在滑移时,接触力会出现非物理振荡[11]。特别地,用有限段法和虚拟体法创建的柔性身管模型的内膛是一串首尾相接的圆柱段,弯曲身管在段与段之间不平滑地过渡,当弹丸通过段间接合部位时会产生非物理的冲击力。为了节省接触计算所用的时间,一些文献采用简化的几何描述方法和接触检测方法。芮筱亭等[12]认为潜在接触点固定地位于定心部中心,根据定心部中心与身管轴线上对应点的距离以及定心部中心的横向速度判断接触状态。陈光宋[13]用圆柱面描述弹丸定心部和炮膛,通过求距离函数的最小值来确定潜在接触点。该方法给出的接触点只出现在定心部的棱线上。
当两物体发生接触时,它们之间会在接触区域中产生接触载荷。在多体动力学中,接触载荷的建模方法可分为两类:①基于接触体几何约束的非光滑离散分析方法[14];②基于接触体表面变形量的连续分析方法[15]。这两类方法在火炮发射动力学中都有使用[16-19],其中连续分析方法居多。一方面,非光滑连续分析方法在处理摩擦问题时存在多解或无解的情况,以及可能违反能量守恒定律的情况;另一方面,非光滑离散分析方法求解的方程维数随接触状态改变,不易于编制程序;连续分析方法中动力学方程的维数固定,易于编制程序,该方法提供的力元可以很高效地植入到通用多体系统动力学程序中去[20-21]。连续分析方法根据接触体的穿透深度计算法向弹性力,必要时根据穿透速率计算阻尼力,以考虑碰撞过程中的能量损失。对于形状简单的几何体,可以根据尺寸、材料参数和恢复系数确定连续分析方法中的刚度系数、幂指数和阻尼系数[22-23]。对于形状复杂的几何体,比如线膛炮的内膛,马佳等[24-26]使用改进的L-N(Lankarani-Nikravesh)模型计算定心部与炮膛的接触力,并使用参数辨识方法,根据仿真数据确定L-N模型中的参数。
依据接触区域尺寸和接触物体尺寸的相对大小,可将接触分为非协调接触和协调接触[27]。当接触区域的尺寸远小于物体的尺寸时,称之为非协调接触。此时接触区域可视作一点,接触物体之间只存在通过接触点的一对相互作用力;接触区域内的接触应力对接触点的力矩忽略不计。当接触区域的尺寸与物体的尺寸相当时,称之为协调接触。弹丸定心部与炮膛的接触即属于此类。对于协调接触,除了考虑接触力,还应考虑接触应力的分布产生的接触力矩。使用静力等效方法可以找出接触力的等效作用点,这个点与前述根据几何形状、物体位置计算出的接触点一般是不一致的。Hippmann[28]使用细化的多边形网格检测接触区域,并根据弹性基础模型在接触区域内施加接触应力载荷。接触应力与穿透深度成比例,对于法线方向在区域内及边界上连续的接触区域可以得出近似正确的应力分布。Hippmann的方法不适用于法线方向不连续的表面,因为那里存在奇异的接触应力[29-32]。弹丸表面在定心部棱线处法线方向不连续,仿真结果表明,弹丸定心部的棱线处存在奇异的接触应力。
本文提出一种计算线膛火炮的弹丸定心部与炮膛接触载荷的模型。该模型包括两部分:①定心部与阳线的接触检测算法;②定心部与阳线之间分布的接触应力的计算方法。给出模型中参数的拟合方法和辨识方法。将接触模型运用于某火炮弹丸发射过程的数值计算,分析弹丸质心偏移与弹丸膛内运动方式和定心部磨损刻痕形成的关系,讨论接触力的等效作用点对摆动力矩计算的影响。
1 定心部与阳线的接触模型
1.1 概 述
膛线是火炮身管内表面的螺旋线,其中凹下的称作阴线,凸起的称作阳线。除了弹带以外,弹丸通过弹体上的环状凸起与阳线发生接触。环状凸起即所谓定心部。对于榴弹炮和加农炮,定心部与炮膛之间的间隙很小,定心部最多会与接近半数的阳线接触,这种接触应归于协调接触的情形。计算弹管之间的接触载荷需要分析接触区域内的应力分布。依据作用的方向,接触应力分为法向接触应力和切向接触应力。法向应力以弹性接触压力为主;剩余部分被认为是黏滞力,以考虑接触中的能量损失。在火炮发射过程中,除了弹丸启动的瞬间,弹炮之间的摩擦都是滑动摩擦,切向接触应力即滑动摩擦力,它与法向接触应力的比值是滑动摩擦因数。Johnson指出,如果两个物体具有相同的弹性常数,那么法向应力的分布不受切向应力的影响;如果两个物体不具有相同的弹性特性,但是摩擦因数明显地小于1,那么切向应力对于法向应力的影响很小,Çömez[31]的计算结果也证实这一点。所以我们忽略法向接触应力与切向接触应力产生的物体变形之间的耦合作用,按光滑接触的情形计算弹性接触压力。
线膛炮的膛线缠角很小,一般加农炮的缠角为5.0°~7.2°,定心部与单根阳线的接触区域可视作一个矩形区域。以155 mm口径的火炮为例,当定心部与一根阳线在膛线的长度方向上完全接触时,接触区域的长度与宽度的比值为10.2,可见接触区域是一个狭长矩形。Borodachev等[33-34]研究了狭长刚性凸模与弹性半空间的接触问题,他们认为狭长区域内的弹性接触压力在宽度方向上具有方根奇异性。然而,根据马佳等的仿真结果,当阳线和定心部接触时,接触压力在阳线的宽度方向上变化较小,没有明显的奇异性;接触压力主要沿着阳线的长度方向变化(如图 1(a)所示)。于是假设弹性接触压力只是阳线长度方向上的函数(如图 1(b)所示)。在这种假设下,只需要关注阳线任意纵截面内的弹性接触压力分布,不失一般性,可以关注过阳线中线的纵截面,如图 1(c)所示。在几何描述上,将炮膛简化成如图 2(a)所示由阳线的中线(后文简称“阳线”)组成的“笼子”。采用这种简化的几何描述,定心部与炮膛之间的空间曲面接触检测问题转变为空间曲面与曲线的接触检测问题。不考虑阳线之间的相互影响,定心部与单根阳线的弹性接触压力根据一个二维接触问题的解析解近似计算。
1.2 弹丸与身管的运动学
物体振动周期接近于碰撞持续时间时,碰撞模型中必须考虑波的传播[35]。以155 mm火炮为例,弹丸定心部和炮膛的碰撞过程时长约0.4 ms,取钢中的纵波波速为5 123 m/s,则碰撞过程中,纵波在身管内传播的距离约为1/4身管长度,因此动力学模型中应考虑身管的柔性;纵波在弹丸内传播的距离约为2.3倍弹丸长度,虽然这个倍数不大,但是在动力学模型中将弹丸视作刚体不影响计算接触力的主要成分。现有文献也多只考虑身管的、不考虑弹丸的柔性。
图3(a)所示是一根柔性身管。图3(a)中用双点划线绘制的是未变形的身管,即参考位形;用粗实线绘制的是变形后的身管,即瞬时位形。瞬时位形上任意一点用单个大写字母表示,例如点J;这一点在参考位形中的位置加注下标“0”,例如点J的初始位置为J0。建立固定坐标系O-xyz和身管的随体坐标系(简称“身管坐标系”)OB-xByBzB,身管坐标系的原点OB位于身管尾部端面的中心,xB轴沿着未变形身管的几何轴线指向炮口。点J在固定坐标系中的位矢为
rJ=rOB+ABrJ,B=rOB+AB(rJ0,B+uJ,B)
(1)
式中:rJ和rOB为点J和OB在固定坐标系中的位矢;rJ0,B和rJ,B为点J0和J在身管坐标系中的位矢;uJ,B为点J在身管坐标系中的变形位移;AB为从身管坐标系到固定坐标系的旋转变换矩阵。将(1)式对时间求导数,得点J的速度
(2)
式中,vJ和vOB为点J和OB在固定坐标系中的速度。
图3(b)所示是一个弹丸。与对身管的分析类似,建立固定坐标系O-xyz和弹丸的随体坐标系(简称“弹丸坐标系”)OP=xPyPzP,弹丸坐标系的原点OP位于弹丸底面的中心,xP轴沿着弹丸几何轴线指向弹丸头部。弹丸是刚体,其上任意一点K处不存在变形位移。点K的位矢和速度分别为
rK=rOP+APrK,P
(3)
(4)
式中符号与式(1)、式(2)两式相同。
根据式(1)和式(3),身管上的点J在身管坐标系和弹丸坐标系中的位矢、速度应满足
rOB+ABrJ,B=rOP+APrJ,P
(5)
(6)
从式(5)、式(6)可解出身管上的点J在弹丸坐标系中的位矢rJ,P和速度rJ,P。同样地,也可解出弹丸上的点在身管坐标系中的位矢和速度。
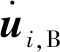
(7)
式中:N为整个身管的形函数矩阵,由单元形函数矩阵组装得到,它是一个6×6(ne+1)矩阵;Φ和Ψ分别为对应平动自由度和转动自由度的形函数矩阵,即分别是N的上三行和下三行元素组成的矩阵[36]。形函数矩阵是Lagrange坐标的函数。式(7)中下标“J”为形函数矩阵在点J处的值。自由度的变化率与自由度采用相同的插值方案,即
(8)
使用式(7)、式(8)可以分析身管上任意一点的变形,包括阳线的变形。现在令J是某根阳线上的点,它的Lagrange坐标满足阳线的参数方程
(9)
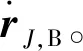
1.3 定心部与阳线的接触检测
图5是定心部与阳线接触检测原理的示意图。接触检测分为两步:①截取可能与定心部接触的阳线段;②判断截取的阳线段与定心部的接触状态。
定心部与炮膛的间隙很小,弹丸在膛内运动时始终和身管保持近乎同轴状态,因此无需考虑阳线横穿定心部的情形。如图 5所示,定心部前、后棱线的圆心是Q和P,过这两点分别作两个垂直于弹丸轴线的平面F和R,分别与阳线相交于点T和S,则与定心部相接触的阳线区域只可能出现在弧线ST上。为了求交点T和S,利用式(5)计算变形后阳线上任意一点在弹丸坐标系中的位矢。设点J是阳线上的任意一点,它在身管坐标系和弹丸坐标系中的位矢分别是rJ,B、rJ,P。因为在任意瞬时rJ,B是xJ0,B的单变量函数,所以rJ,B也是xJ0,B的单变量函数,即有rJ,P=rJ,P(xJ0,B)。点S和T在身管坐标系中的坐标xS0,B、xT0,B应分别满足方程
xJ,P(xS0,B)=xP,P
(10)
和
xJ,P(xT0,B=)xQ,P
(11)
式(10)和式(11)需要使用数值方法求解。将点P和Q的位矢rP,P、rQ,P变换为rP,B、rQ,B,然后以xP,B和xQ,B作为数值求解时的迭代初值可以在较少的迭代步数内收敛。
定心部与阳线的接触状态取决于曲线ST与定心部圆柱面的最小距离,这涉及求解最优化问题。为了避免低效的数值寻优过程,采用一种简化方法判断定心部与阳线的接触状态。由于膛线的缠角很小,曲线ST近似为一段直线。例如,155 mm弹丸的定心部长度为40 mm,在这个长度范围内,曲线ST的直线度为32 μm,直线度对长度的比值仅为0.000 8。将曲线ST沿着弹丸的半径方向投影到定心部表面,得曲线S′T′。类似地,曲线S′T′也近似为一段直线。于是定心部与阳线的接触检测问题转化为直线段S′T′与ST的接触检测问题。这两个直线段的位置关系取决于它们端点的位置关系。定义S、T两点与定心部的干涉量,分别为
(12)
和
(13)
式中,rb为定心部的半径。定心部与阳线发生接触的判据是δS和δT中至少有一个大于零。当接触发生时,定心部与阳线的干涉量为
δ=max(δS,δT)
(14)
1.4 定心部与阳线的接触应力
为了计算定心部与阳线的接触应力,首先需要确定法向弹性接触压力。将弹丸和身管在接触区域附近沿着定心部的圆柱面展开,如图 6所示。定心部与阳线的弹性接触压力按二维问题计算,二维物体的轮廓即是图 6中过阳线中线的纵向截面内弹丸与身管的截面轮廓,即阴影部分的轮廓。
根据压入阳线的定心部棱线数量,定心部与阳线的接触状态可分为两类:不完全接触和完全接触。当定心部只有一个棱线压入阳线时,定心部与阳线不完全接触(见图 7(a));当定心部的两个棱线都压入阳线时,定心部与阳线完全接触(见图 7(b))。图 7中:2a为接触区域的长度;2b为定心部在阳线长度方向上的长度
(15)
式中,β为膛线的缠角。等齐膛线的缠角是恒定的;渐速膛线和混合膛线的缠角是变化的,但是在定心部范围内变化很小。所以β取接触区域中点处的缠角。当不完全接触时,仅在接触区域右端阳线轮廓的法线方向不连续,因此接触压力在右端奇异,在左端连续地降至零。a随着定心部与阳线的相互压入深度的增大而增大。当完全接触时,在接触区域两端阳线轮廓的法线方向都不连续,接触压力在两端都奇异。a不随压入深度变化。
在计算弹性接触压力前,先给出一些参数的含义和符号表示。如图 8所示,定心部(物体1)在力F和力矩M的作用下以倾斜角度κ与阳线(物体2)发生接触。弹炮间隙很小,κ≈0,所以认为定心部轮廓的法线方向近似沿着竖直方向。
(16)
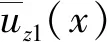
弹性边界法向位移与干涉量存在以下关系
(17)
对于如图 8所示的定心部倾斜方向,式(17)右端括号内取“-”号;对于相反的倾斜方向,即定心部左侧棱线先与阳线接触时,式(17)右端括号内取“+”号。关于接触压力与弹性边界的法向位移,假设以下两个积分方程在接触区域内近似成立
(18)
(19)
式中,E1和E2为等效弹性模量,不仅与物体的材料有关,还与物体的几何形状有关。将式(18)和式(19)分别除以E1和E2,然后相加,并令
(20)
可得
(21)
式(21)的解为
(22)
其中,
(23)
式(22)的分母表明接触压力具有方根奇异性。弹性接触压力与接触力之间满足
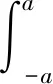
(24)
因此,式(22)事实上给出了接触力F与接触半长度a的关系。而当几何形状给定时,接触半长度a应只与干涉量δ相关,所以需要引入F与δ的关系,即考察定心部与阳线的局部接触刚度。
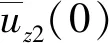
(25)
式中,K2(h2/a)为阳线的无量纲刚度函数,括号中h2/a为身管的无量纲壁厚。对于定心部,如果弹丸内壁相对于弹丸不发生径向变形,接触力与接触中心位移应具有与阳线类似的关系,即
(26)
式中,K1(h1/a)为定心部的无量纲刚度函数,括号中h1/a为定心部的无量纲壁厚。事实上,弹丸是薄壳结构,其内壁在接触载荷下会向内凹陷,因此定心部的接触力与接触中心位移的关系应修正为
(27)
式中,η为定心部的刚度折减系数。将式(25)、式(27)代入式(17),得
(28)
令
(29)
则
(30)
文献[37]认为碰撞力只与弹丸刚度有关,然而根据(30)式,定心部和阳线的接触刚度同时受定心部壁厚和身管壁厚影响。轴-孔协调接触是与定心部-身管接触相类似的情形,文献[38-39]从理论分析、数值计算和试验验证3个方面证明轴-孔接触刚度随孔的壁厚变化。现代火炮身管是变截面的,所以在弹丸发射过程中,定心部-阳线接触刚度随着弹丸的膛内行程改变。
当定心部与阳线不完全接触时,p(∓a)=0,于是λ*=1,此时
(31)
将式(30)、式(31)联立,得方程
(32)
式(32)给出了不完全接触时干涉量δ与接触区域半长度a之间的隐式关系。令式(32)中的a等于定心部的半长度b,这时满足式(32)的δ是一个临界值,记为δcr。该临界值可显式地写为
(33)
当δ≤δcr时,定心部与阳线是不完全接触状态,a为式(32)的解。式(32)是隐式方程,需要使用数值方法求解。当δ>δcr时,定心部与阳线是完全接触状态,a=b。确定了接触区域的半长度后,将之代入式(22)计算压力分布。
下面计算定心部与阳线的接触应力。如图9所示,灰色曲面是定心部的局部,曲线CD是与定心部发生接触的阳线段,它与图 5中曲线ST的关系取决于定心部与阳线的接触状态。当定心部与阳线完全接触时,曲线CD就是曲线ST;当定心部与阳线不完全接触时,曲线CD只是曲线ST上的一段。例如,定心部先与点T发生接触,则点D就是点T,xC0,B=xD0,B-2acosβ;反之,定心部先与点S发生接触,则点C就是点S,xD0,B=xC0,B+2acosβ。将曲线CD沿着弹丸半径方向投影到定心部的圆柱面上,得到曲线GH。阳线上任意一点J的投影是点K。点J相对于点K的速度为vKJ,它可以分解为法向相对速度vKJn和切向相对速度vKJt。定心部在点K处受到的接触应力为fK,相应地,阳线在点J处受到的接触应力为fJ,fJ=-fK。与相对速度类似,fK分解为法向应力fKn和切向应力fKt。
碰撞过程中往往伴随着能量损失,能够引起能量损失的因素包括应力波传播、塑性变形、材料阻尼、声辐射与热传导等[40-41]。可见能量损失是一个复杂的现象,充分考虑各种损耗因素是很困难的工作。在接触力的连续分析方法中,引入阻尼力来考虑能量的损失[42-45]。阻尼力除了与物体的相对碰撞速率成正比,一般还与弹性接触力成正比。后者的目的是使接触力在物体相互分离前连续地降至零,避免两物体黏着。因此,法向应力按式(34)计算
(34)
式中:c为阻尼系数;eKn为定心部圆柱面在点K处的单位法向量,指向定心部外;vref=1 m/s,其作用是使c成为一个无量纲数。弹性接触压力p的计算方法已经由式(22)给出了。计算弹性接触压力时,横坐标取
(35)
切向应力即摩擦力,计算式为
(36)
式中:eKt为切向相对速度方向上的单位向量;μ为摩擦因数,由修正的Coulomb摩擦模型计算[46]。
将法向接触应力和切向接触应力相加,最终得到接触应力fK。式(34)、式(36)表明,fK主要与弹性接触压力p成比例,因而也具有方根奇异性。fK方向取反即得fJ。
1.5 定心部与阳线受到的接触载荷
定心部与阳线受到的接触载荷是接触应力在接触区域内的曲面积分。因为假设接触应力在阳线的宽度方向上不变,曲面积分可转化为曲线上的积分。首先讨论定心部受到的接触载荷。如图 10(a),深灰色矩形是接触区域。接触应力对弹丸坐标系原点Op的力和力矩分别为
(37)
(38)
式中:wn为阳线的法向宽度,它与阳线的端面宽度w1的关系是wn=w1cosβ;l为曲线GH的自然坐标。曲线GH上点K处的切向量drK,P/dxJ0,B是曲线CD上点J处的切向量drJ,P/dxJ0,B在定心部上的投影,自然坐标l对xJ0,B的导数为
(39)
利用式(39)可将式(37)、式(38)改写为
(40)
(41)
图10(b)绘制了阳线上接触区域内受到的接触应力。因为柔性身管由有限单元法建模,阳线受到的接触载荷需转换成节点载荷列阵,即
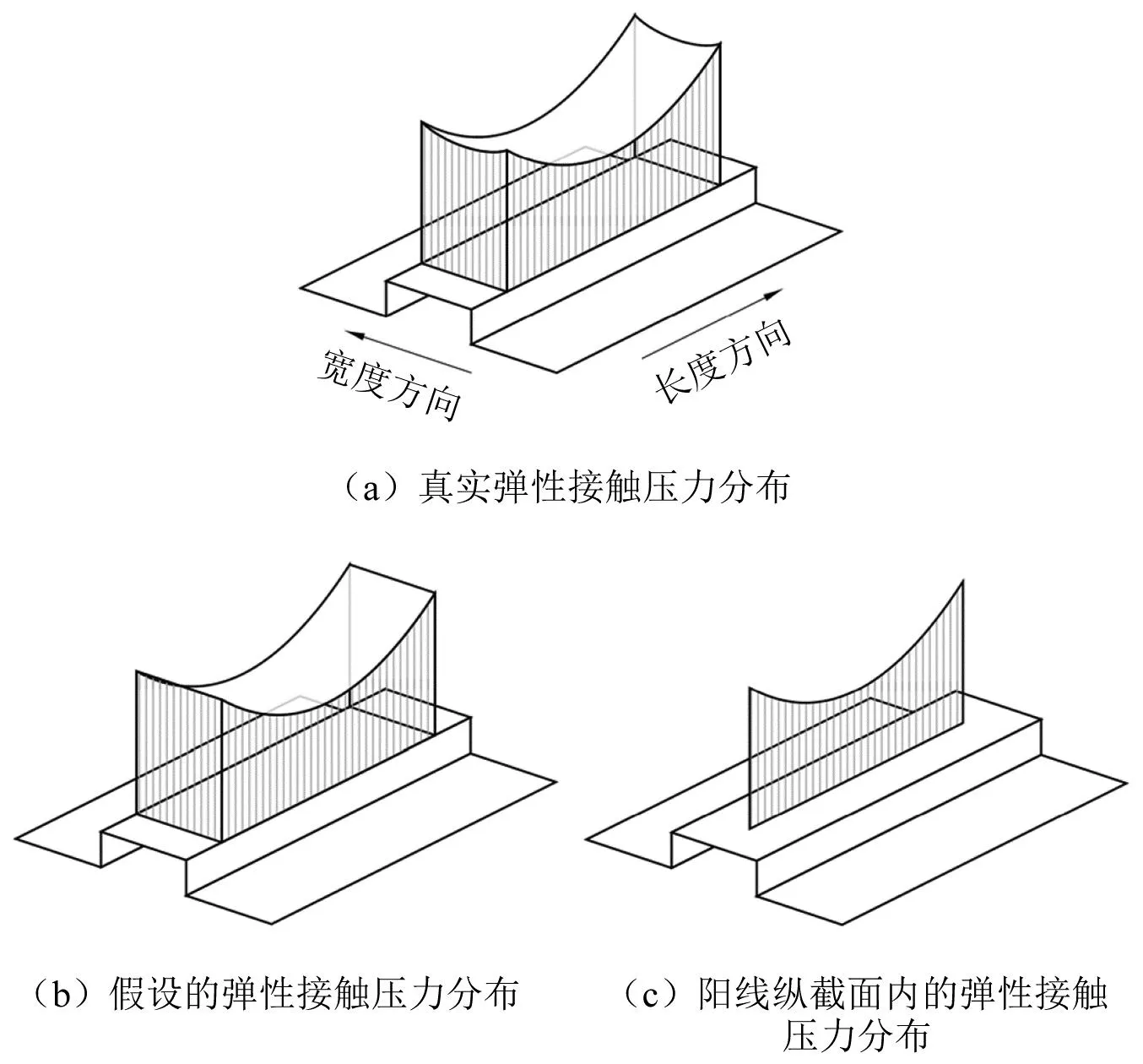
图1 接触压力的简化 Fig.1 The simplification of the contact-pressure
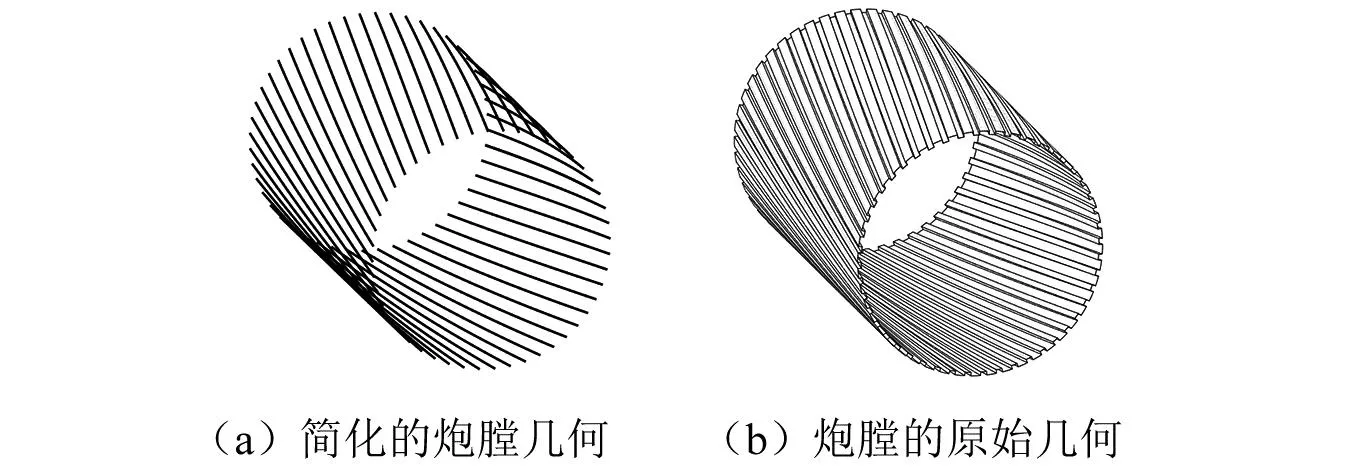
图2 炮膛的简化Fig.2 The simplification of a bore
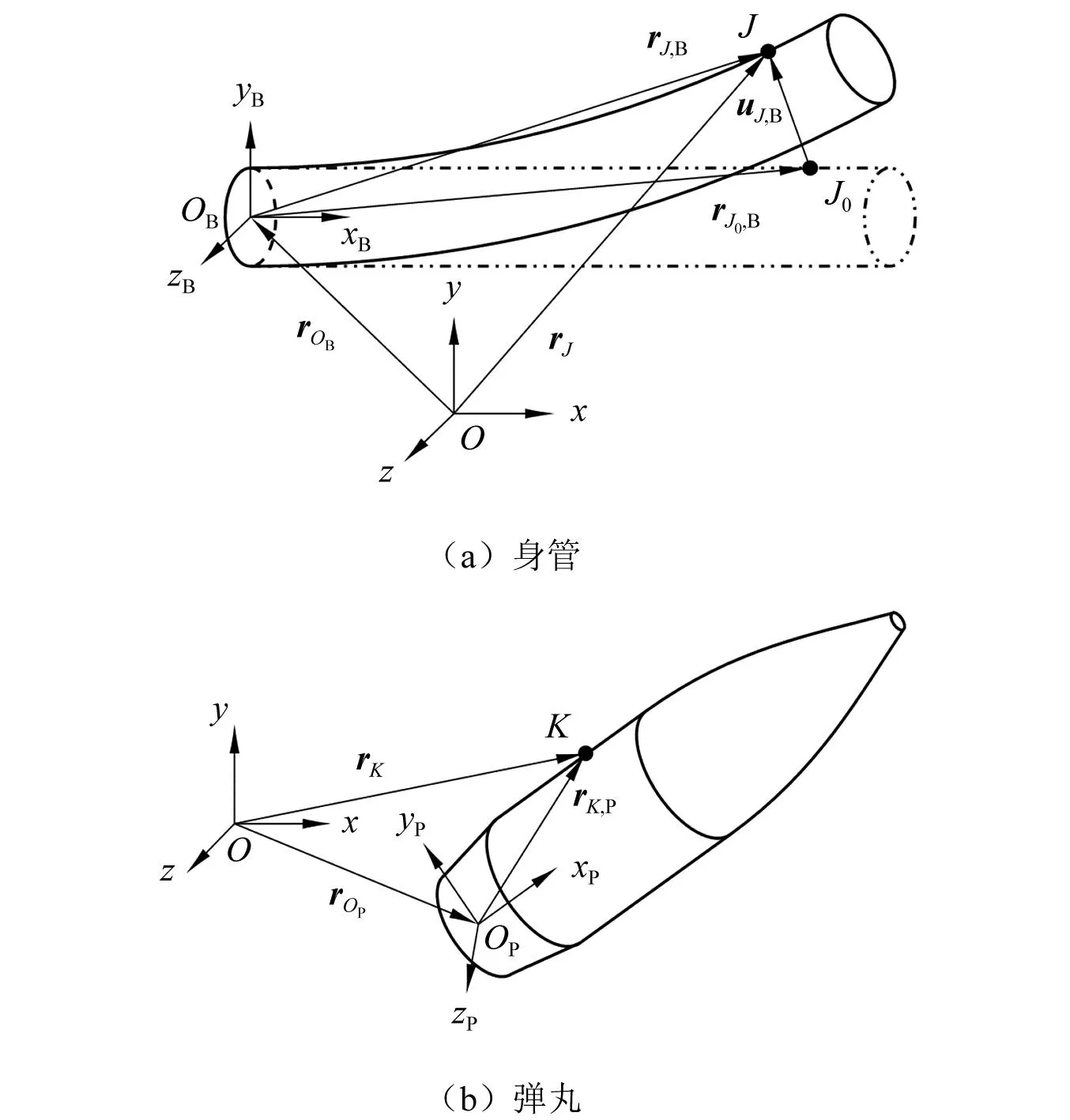
图3 身管和弹丸的运动学Fig.3 Kinematics of a barrel and a projectile
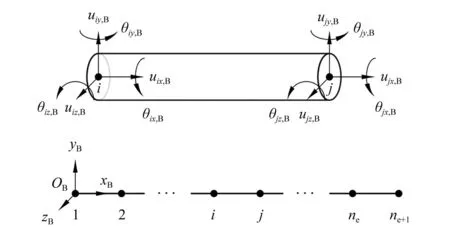
图4 身管的有限单元离散模型。Fig.4 A finite-element discretization of a barrel.
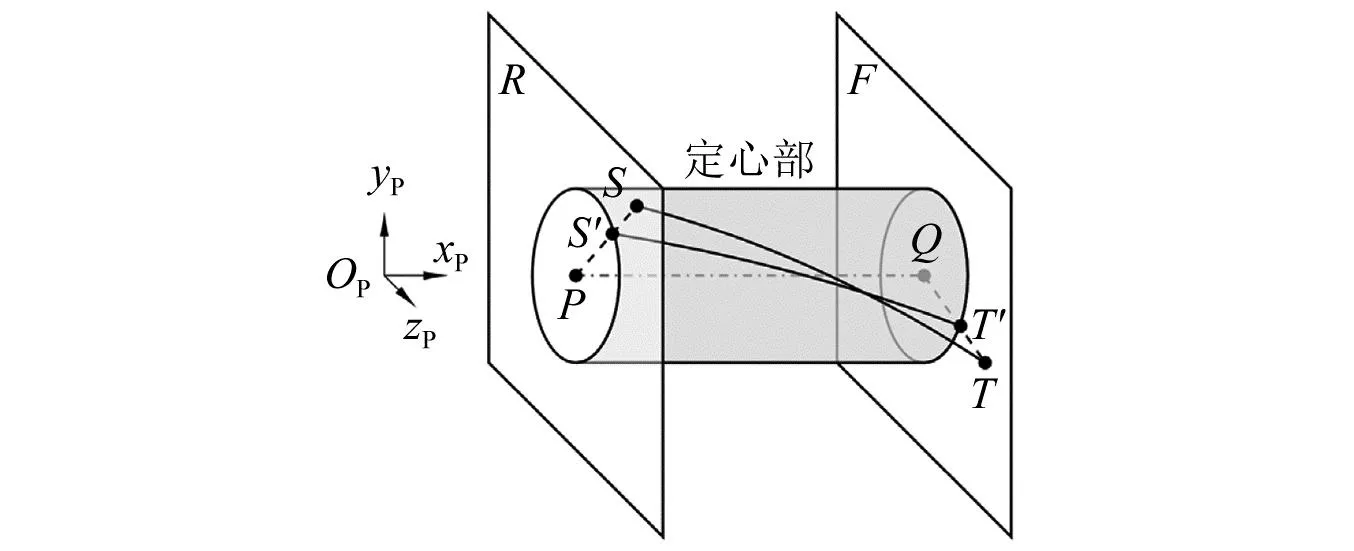
图5 定心部与阳线的接触检测Fig.5 Contact detection of a bourrelet and a rifling land
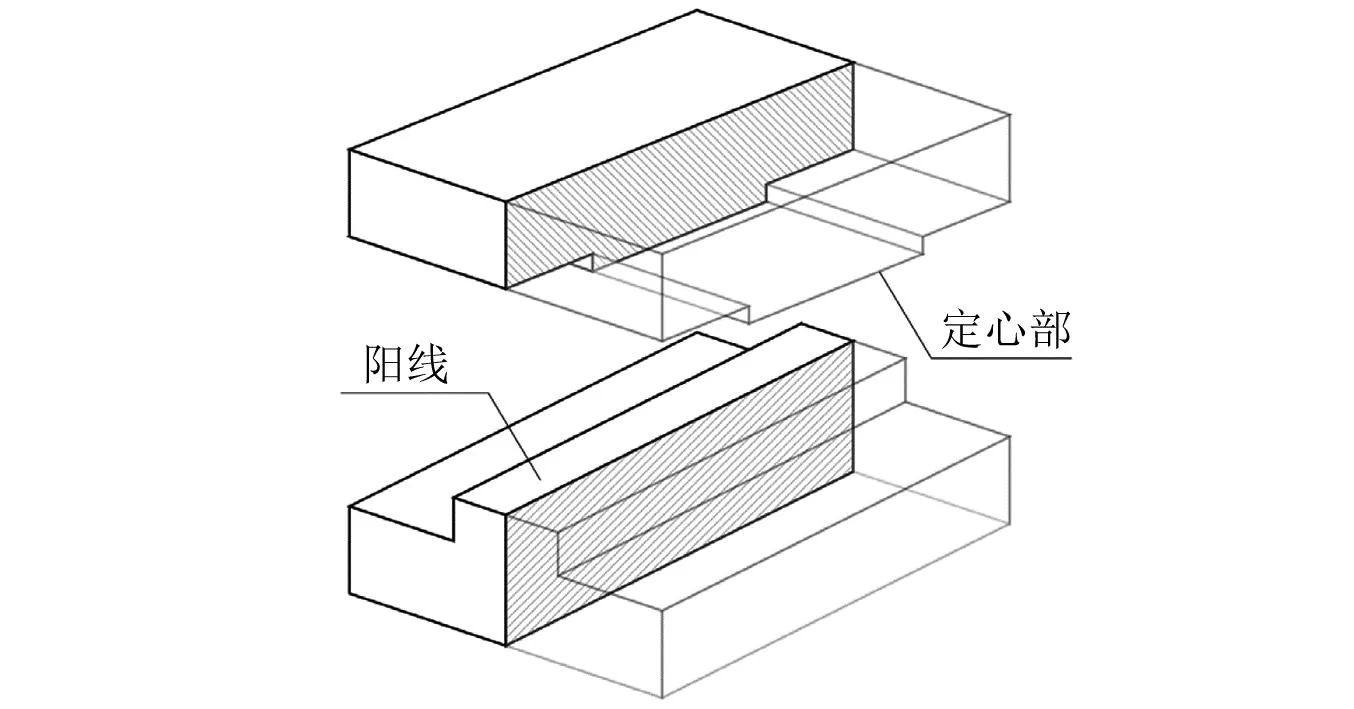
图6 沿定心部圆柱面展开的弹丸与身管Fig.6 A projectile and a barrel spread out along the cylindrical surface of the bourrelet
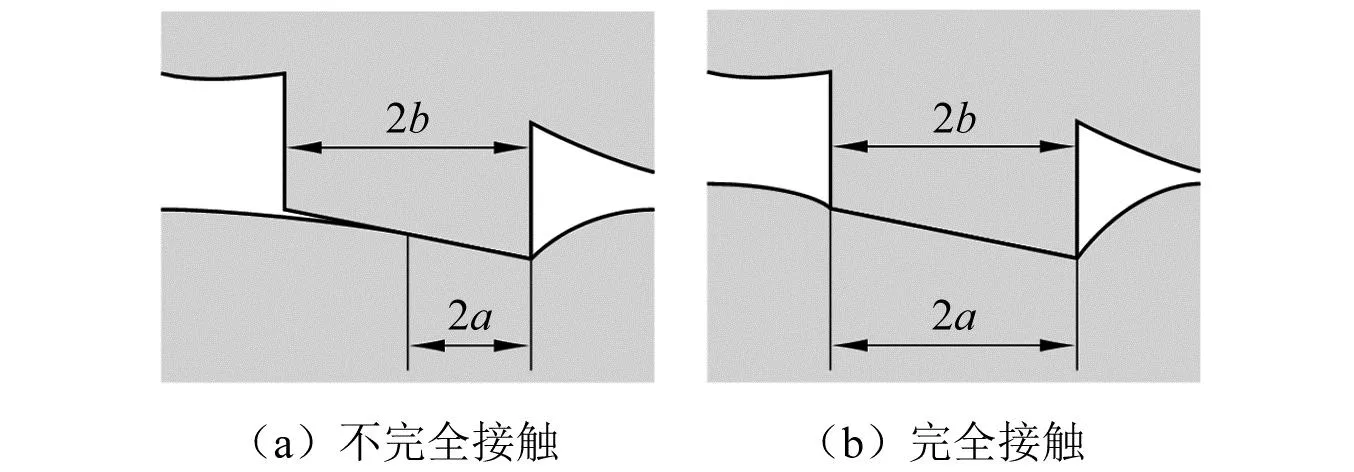
图7 接触类型Fig.7 Contact type
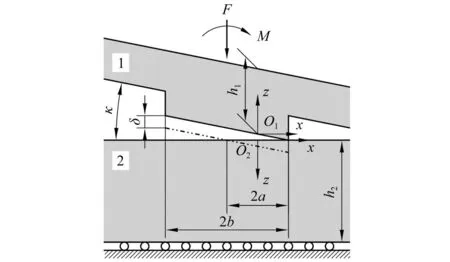
图8 计算弹性接触压力的示意图Fig.8 A sketch for calculating the elasticity contact pressure
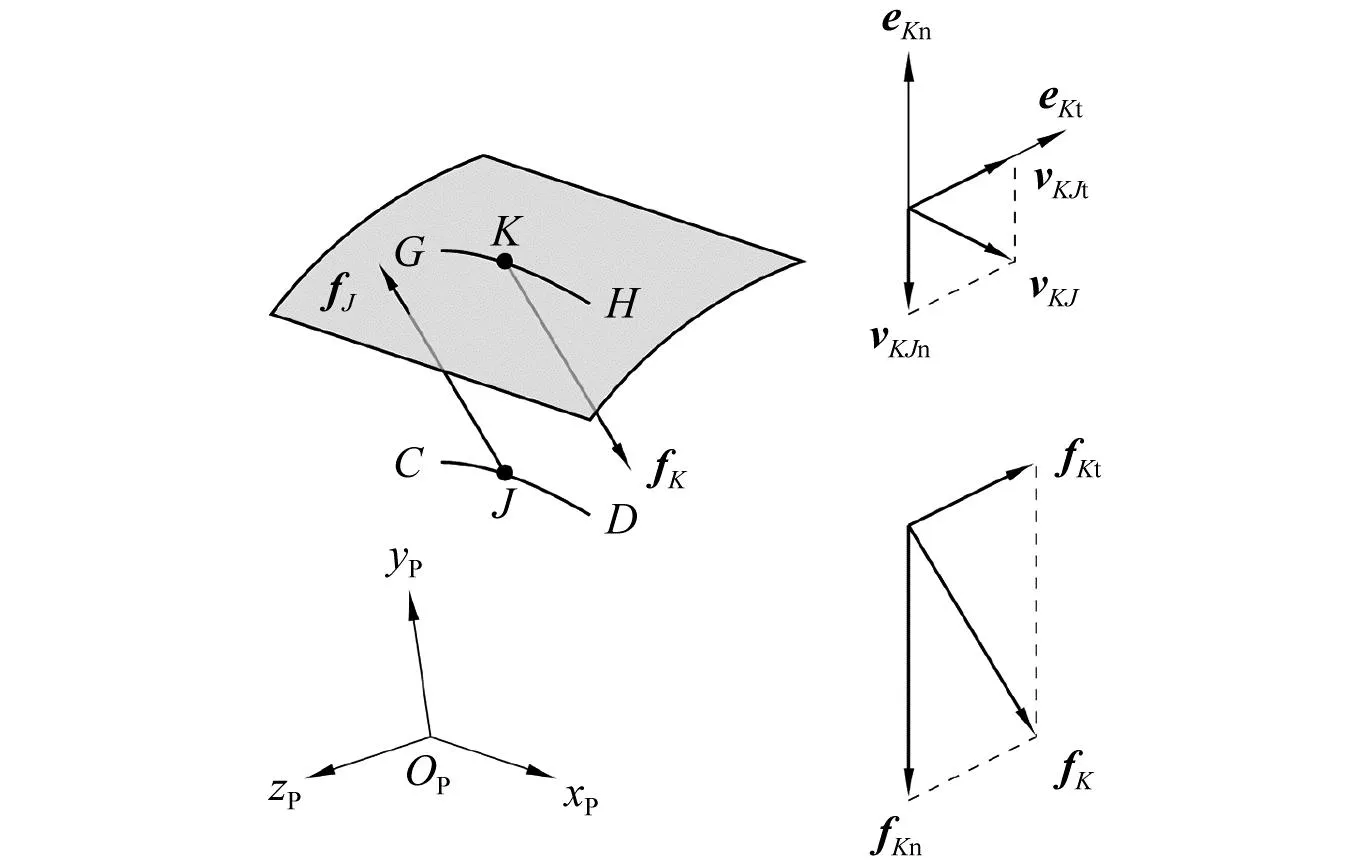
图9 计算接触应力的示意图Fig.9 A sketch for calculating the contact stress
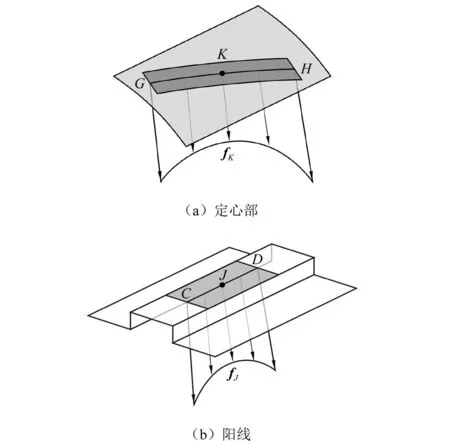
图10 定心部上和阳线上的接触应力Fig.10 Contact stress on the bourrelet and rifling land
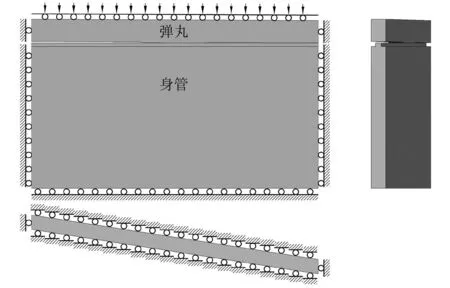
图11 静态接触问题的几何与边界条件Fig.11 The geometry and boundary conditions of a static contact problem
(42)
式中:QB为接触载荷的节点载荷列阵;s为曲线CD的自然坐标,它对xJ0,B的导数为
(43)
将式(43)代入式(42),得
(44)
式(40)、式(41)和式(44)中的积分由数值积分方法计算近似值。3个被积函数因为fJ、fK的存在而具有方根奇异性,数值积分方法选取第一类Chebyshev-Gauss公式。首先引入变换
(45)
将三式的积分化成标准形式
(46)
(47)
(48)
式(46)~式(48)的数值积分格式为
(49)
(50)
(51)
式(49)~式(51)中,ξi是第一类Chebyshev-Gauss积分的节点
(52)
ωi为权重系数
(53)
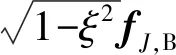
式(49)~式(51)给出的是单根阳线的接触载荷。对所有阳线遍历求和,即得定心部与整个炮膛的接触载荷。
2 参数拟合与辨识
第1章的接触模型中待确定的参数或函数有等效弹性模量E1、E2、无量纲刚度函数K1、K2、刚度折减系数η和阻尼系数c。本章以某火炮为155 mm例,确定这些参数与函数。其中,等效弹性模量和无量纲刚度函数根据一组静态接触问题的数值计算结果进行拟合,刚度折减系数和阻尼系数根据文献中的数据、使用参数辨识方法确定。
2.1 拟合等效弹性模量与无量纲刚度函数
使用ABAQUS软件完成一组静态接触问题的数值计算,产生的数据用于拟合等效弹性模量和无量纲刚度函数。这些参数或函数描述的是定心部与阳线的局部接触刚度,所以数值计算所用的几何不必包含完整的弹丸和身管。如图 11所示,将弹丸和身管沿着定心部和圆柱面展平,模型的几何在轴线方向只取关于定心部中心对称、5倍于定心部长度的范围,在圆周方向只取一根膛线的范围。定心部的倾斜角度取κ=0.002 rad和κ=0.005 rad两个角度,身管的外圆半径在110~180 mm内间隔10 mm取值,即一共16种尺寸组合。弹丸材料与身管材料的力学参数相同,弹性模量为206 GPa,Poisson比为0.3。在定心部表面与阳线表面之间添加接触载荷。使用增广Lagrange乘子法,刚度缩放因子设置为1 000。在身管的外壁处(底部边界)约束竖直方向的位移;在弹丸和身管的左右/前后边界处约束左右/前后方向的水平位移;弹丸内壁(顶部边界)强制施加竖向位移,位移从0~0.5 mm线性地增加。为了捕捉两种接触状态切换的过程,输出了20个时间帧的过程数据。划分网格时选择完全积分的一阶六面体单元。为了提高端部接触压力的计算精度,在端部布置细化的网格,如图12所示。

图12 有限元网格划分Fig.12 Finite element meshing
在不完全接触阶段,λ*=1,由式(23)
(54)
在接触模型中,E*是独立于载荷的一个参数,但是根据数值结果,它随着接触区域的长度变化。为了简化模型,只取当干涉量达到临界值时的计算值。对16种尺寸组合的计算值取算术平均,得E*=3.222×1011Pa。
由式(18)、式(19)可知
(55)
因此只要确定两个x方向梯度的比值,再结合式(20),即可确定E1和E2。根据数值结果,定心部和阳线在接触区域内的轮廓可近似为二次曲线,用过轮廓端点的割弦斜率作为梯度的平均值。对16种尺寸组合的结果取算术平均,得E1=8.073×1011Pa,E2=5.362×1011Pa。
在静态接触问题的数值计算中,对弹丸内壁上的节点施加的是相同的强制位移,所以弹丸内壁不发生径向变形。无量纲刚度函数可从式(25)、式(26)得出。图13绘制了无量纲刚度函数与无量纲壁厚的关系。图13中每一个数据点对应一种尺寸组合的一个时间帧,共计320个数据点。用幂函数拟合两个无量纲刚度函数,结果如图13中曲线所示。图 13(b)中数值结果的数据点集中在拟合曲线附近,说明1.4节中借助量纲分析法得出的接触力与接触中心位移的关系是合理的。无量纲刚度函数的拟合表达式分别为
图13 拟合定心部和阳线的无量纲刚度函数Fig.13 Fit the dimensionless stiffness function of the bourrelet and rifling land
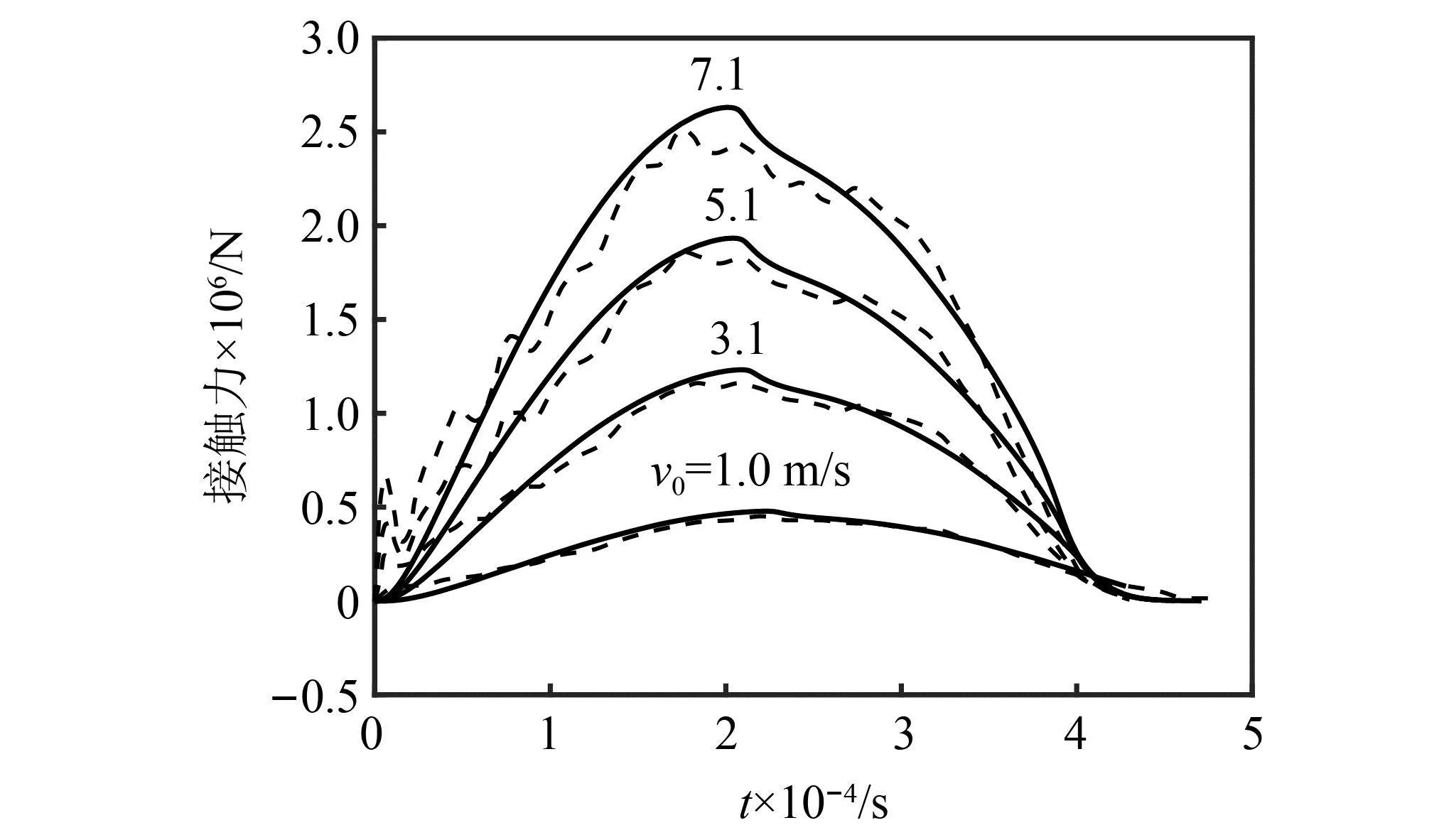
图14 前定心部与身管的接触力(虚线文献[26]的仿真,实线本文接触模型)Fig.14 Contact force between the front bourrelet and barrel (Dashed lines-the simulation in reference [26]; solid lines-the contact model in current paper)
(56)
(57)
两者的R2分别为0.998和0.987。
2.2 辨识刚度折减系数和阻尼系数
刚度折减系数和阻尼系数是两个经验修正系数,很难通过理论分析计算它们的数值。2.2节运用参数辨识方法反求这两个参数。
首先建立参数辨识问题。将待辨识参数写成列矩阵的形式
I={ηc}T
(58)
(59)
式中,τ为一次完整碰撞过程的时长。参数辨识的目的是在给定范围内寻求使误差函数最小的待辨识参数,即是求解以下问题
(60)
使得
Ilb≤I≤Iub
(61)
式中,Ilb、Iub为待辨识参数的上、下边界。
文献[26]提供了4种横向初速度下前定心部与身管相撞的接触力历程。选取其中初速度v0=5.1 m/s时的接触力作为参数辨识问题的输入数据,其他3组数据用于验证本文接触模型及参数拟合、辨识的结果。式(60)可视作一个优化问题。使用遗传算法求解的结果为η=0.044 8,c=0.008 8。
使用本文的接触模型计算了四种横向初速度下前定心部与身管相撞的接触力,与文献仿真数据的对比结果见图 14。可以看出,本文结果与文献结果在时间宽度和接触力幅值上相符合。接触模型计算的接触力曲线在峰值之后有一段凹陷,文献中的结果也有相近的变化趋势。
表1列出了按式(59)计算的误差函数值。参数辨识只使用了v0=5.1 m/s的仿真结果,而4种横向初速度的误差函数水平相当,表明经过标定的接触模型适用于典型横向速度范围内定心部-身管接触问题,验证了本文接触模型及其参数拟合、辨识方法的正确性。与仿真结果不同的是,本文的接触模型将弹丸描述成刚体,图 14中的接触力曲线光滑,没有复现出接触力波动的现象。使用刚体弹丸模型只能计算接触力的主要成分。

表1 误差函数
3 数值算例与分析讨论
本章将接触模型运用于弹丸发射过程的计算。为了排除身管后坐引起的扰动,将身管尾部端面固定。身管坐标系的xB轴水平,zB轴竖直向上,即身管是一根悬臂梁。初始时刻弹丸坐标系的姿态与身管坐标系的姿态相同。整个系统在重力作用下达到静平衡后,弹丸在火药燃气压力的推动下向前运动。燃气压力数据来自内弹道程序的计算结果。不考虑挤进过程,即弹丸启动时弹带已完全嵌入膛线。弹带与身管的接触载荷简化为弹簧阻尼力元。为了保障弹丸顺畅地运动,定心部和炮膛的总间隙设为0.2 mm。
图15是计算得到的弹丸在膛内运动时弹丸回转轴的摆动轨迹,弹丸质心在其yP轴上偏移量e为-0.15 mm。图15与文献[47]给出的弹丸膛内摆动轨迹测试结果(文献图5)在两个方面相符。首先,弹轴摆动的范围相符,横向、纵向摆角的幅度均约为8′。其次,摆动轨迹具有相同的演化模式:弹轴在起点以横向摆动为主,至终点时弹轴以类圆周方式摆动。可见使用本文的接触模型能较准确地反映弹丸膛内运动规律,验证了接触模型的有效性。
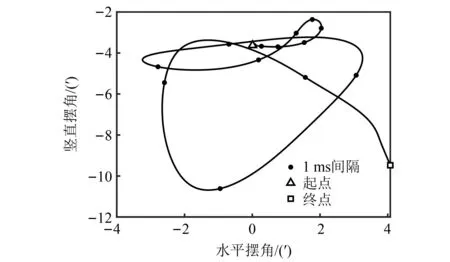
图15 弹丸膛内摆动轨迹Fig.15 A swinging trajectory of projectile in bore
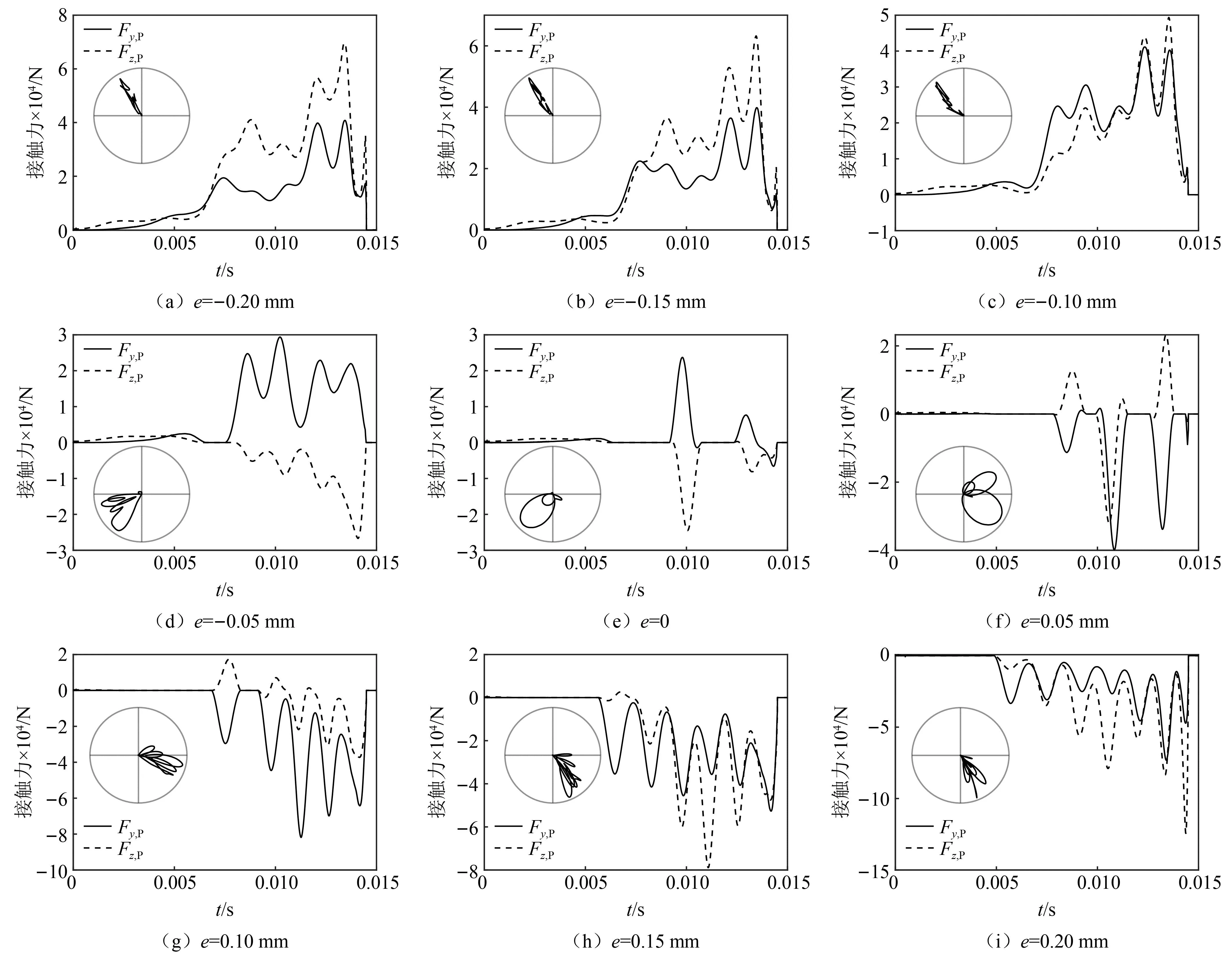
图16 前定心部受到的横向接触力(极坐标图中是从弹尾看到的横向力矢端在弹丸坐标系中的轨迹)Fig.16 Lateral contact force on the front bourrelet (The polar diagrams present the trajectories of vector tip of the lateral force in the projectile frame when one facing the projectile bottom)
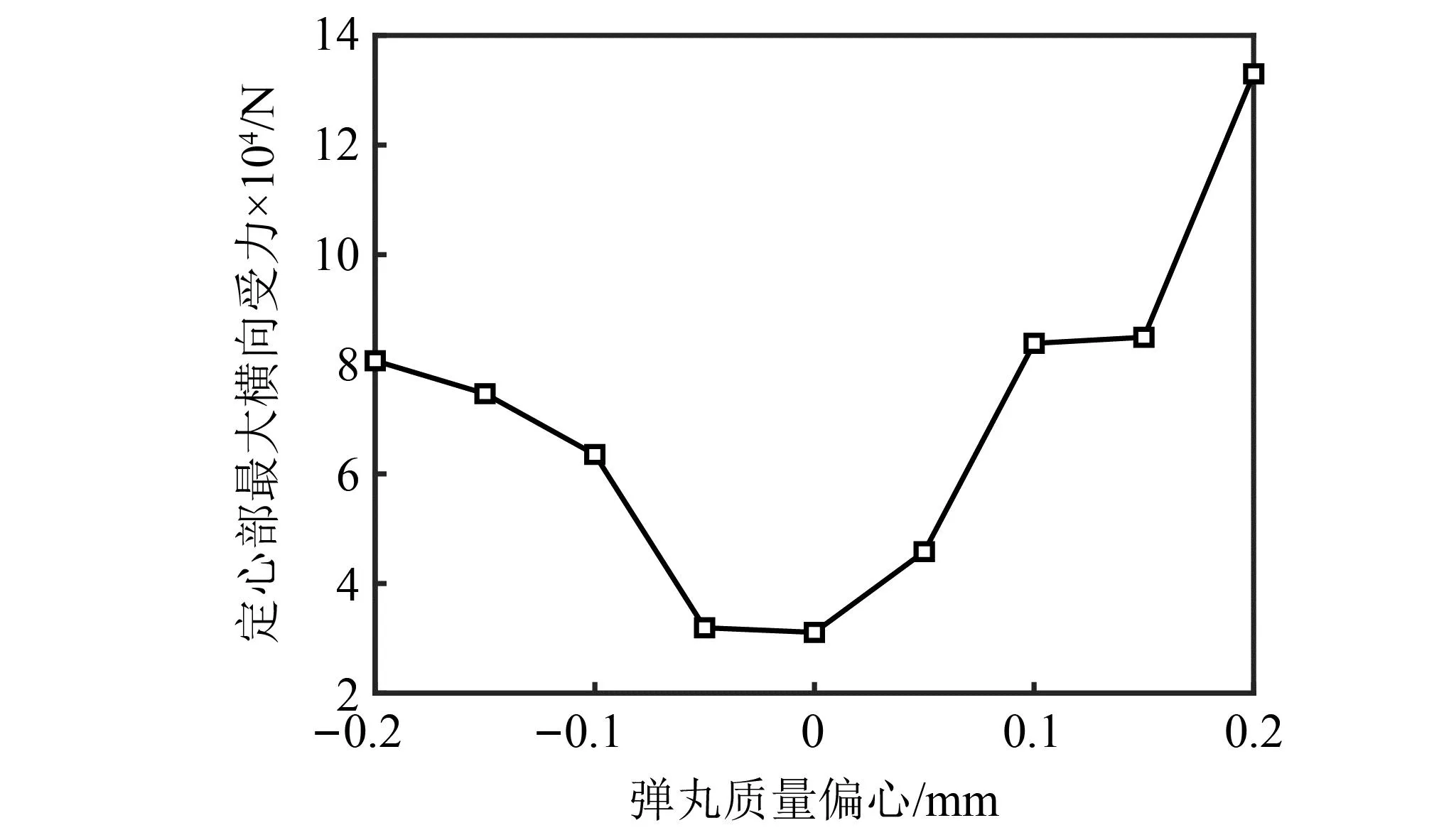
图17 前定心部最大横向力与弹丸质心偏移量的关系Fig.17 The maximum lateral force on the front bourrelet vs. mass-center bias of the projectile
考虑弹丸质心在zP轴方向上的偏移,偏移量e在-0.2~0.2 mm内每隔0.05 mm取值。计算结果表明,内弹道过程中后定心部不与炮膛发生接触。图 16绘制了前定心部受到的横向接触力历程曲线,可以看到横向力在弹丸发射时周期性地波动,表明弹丸轴线在膛内摆动。前定心部与炮膛的接触类型可分为贴膛和碰撞两类。这里根据弹丸轴线的摆动现象给出这两类接触类型的定量区分方式:如果弹丸轴线在接触时间内完成一个周期以上的摆动(不含一个周期),则定心部发生贴膛接触;否则定心部发生碰撞接触。当e=-0.2 mm、-0.15 mm、-0.1 mm时,前定心部始终与炮膛接触,这种属于贴膛接触。当e=-0、+0.05 mm时,前定心部与炮膛断续接触,这种属于碰撞接触。当e=-0.05 mm、+0.1 mm、+0.15 mm、+0.2 mm时,两种接触类型都会出现,定心部首先与炮膛碰撞接触,在内弹道中后期转为贴膛接触。弹丸质心的偏移量越大,前定心部越可能以贴膛的方式与炮膛接触。在贴膛接触时,前定心部受到的横向力相对弹丸的摆动角度范围在60°以内,所以前定心部大约以一半固定的圆周与炮膛接触;另一方面,弹丸质心偏移量的绝对值越大,则前定心部受到的最大横向力越大(如图 17所示),结果导致,质心偏移量较大的弹丸的前定心部可能在一侧出现磨损刻痕(文献[19],图8),刻痕深度与质心偏移量呈正相关。这种不对称的刻痕会对弹丸的气动特性带来不利影响。
如1.1节所述,定心部与炮膛的接触属于协调接触,不存在“接触点”。根据静力等效的原则定义这样一个接触力的等效接触点:当接触力集中于这一点作用于弹丸时,它对弹丸坐标系原点的力矩等于分布的接触应力对弹丸坐标系原点产生的力矩,并且这一点位于定心部表面的接触区域内。记这一点为U,它在弹丸坐标系中的坐标应满足如下方程组
(62)
式(62)一般有两个解,取落在接触区域中的那个解。图 18给出了前定心部上的等效接触点在弹丸坐标系中的轴向位置随时间变化的历程曲线,图18中还给出了前定心部的两个棱及其中心的位置。等效接触点轴向位置曲线的不连续部分对应前定心部与炮膛脱离接触的时期。可以看出,等效接触点的轴向位置既不固定位于前定心部中心,也不会落在前定心部的两个棱线上,而是在前定心部中心前方的一小段范围内变化;它的位置变化与弹丸轴线的摆动相关。等效接触点轴向位置与前定心部中心之间的偏差表明,定心部倾斜着与阳线接触,导致接触载荷关于前定心部中心不对称。这可由文献[19]的图8(b)得到验证,图中前定心部上的刻痕前深后浅,接触载荷偏向定心部前端。等效接触点的平均位置在xU,P=0.380 1mm处,如果保持横向力的大小和方向不变,将它的作用点移动到前定心部的中心,那么横向力对弹丸质心的摆动力矩变化将达到9.62%;如果将横向力的作用点移动到前定心部的前棱和后棱上,那么摆动力矩的变化将分别达到44.31%和63.56%。
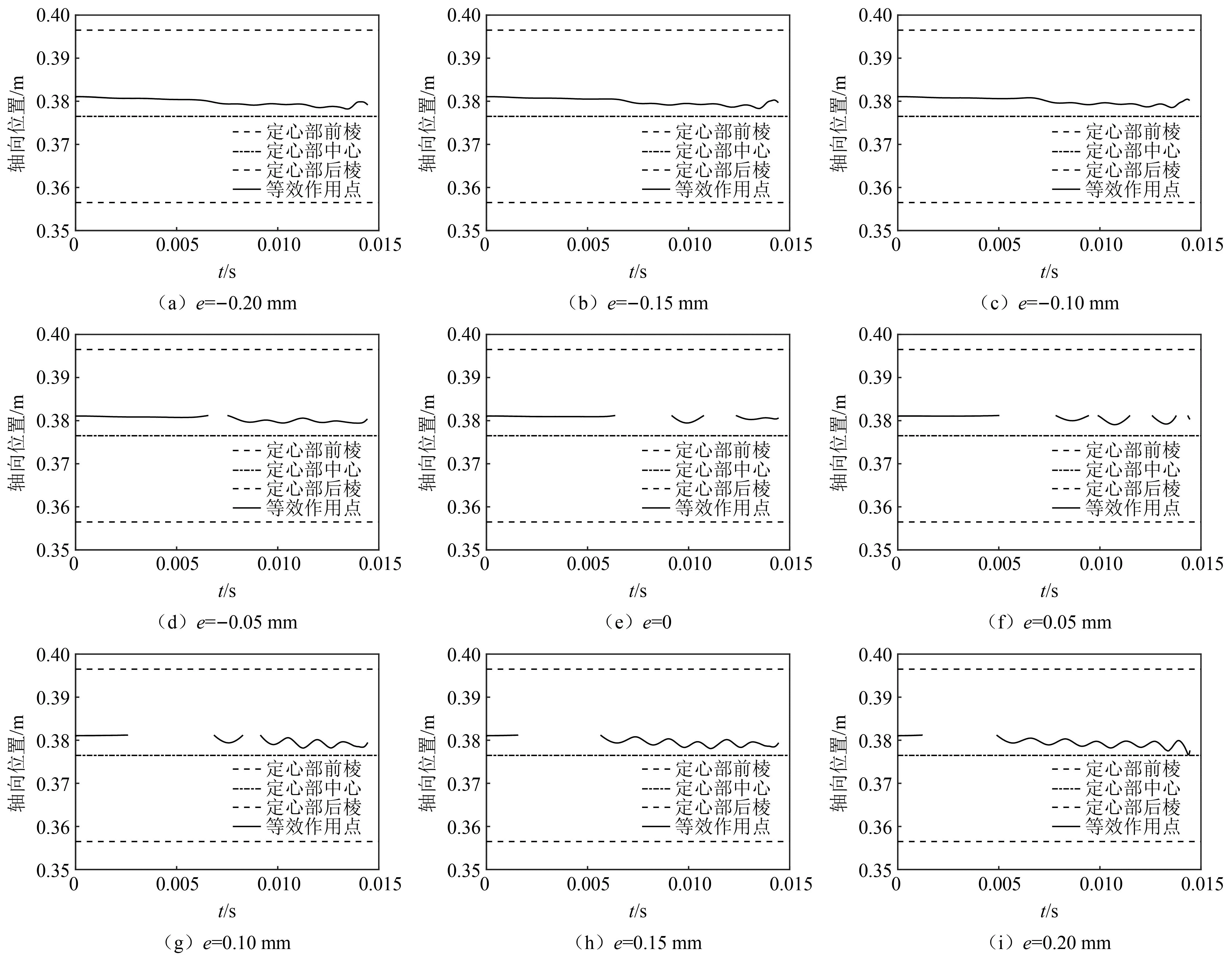
图18 等效接触点在弹丸坐标系中的轴向位置Fig.18 The axial location in the projectile frame of the equivalent contact point
4 结 论
本文提出了一个用于线膛炮弹丸定心部与炮膛接触问题的近似模型,其近似性体现在以下几点:
(1)将柔性身管简化成一维的Euler-Bernoulli梁;将弹丸视作刚体,引入半经验的刚度折减系数来考虑定心部的局部柔性。
(2)将阳线表面抽象成一组空间曲线,简化阳线与定心部表面的接触检测。
(3)假设接触压力只沿着膛线的长度方向变化;将弹丸与身管沿着定心部圆柱面展开,使用一个二维接触问题的解析解计算定心部与阳线的接触压力。
(4)引入半经验的阻尼系数以考虑碰撞过程中的能量损失。
使用拟合方法和参数辨识方法确定了接触模型中的待定参数,并将接触模型的计算结果与文献中的仿真结果进行了对比,验证了模型的正确性。最后将经过标定的接触模型运用于弹丸发射过程的计算。根据本文的工作内容,可以得出以下结论:
(1)定心部和阳线的接触刚度同时受定心部壁厚和身管壁厚影响。对于给定的弹种,定心部-阳线接触刚度依弹丸的膛内行程改变。
(2)只有前定心部与炮膛发生接触,并且前定心部上的接触区域相对固定。弹丸质心的偏移量影响前定心部与炮膛的接触方式。质心偏移量越大,前定心部越可能发生贴膛接触,所受的横向接触力也越大。极端条件下,前定心部会被阳线磨损出刻痕。
(3)按照静力等效原则定义的前定心部与炮膛间的等效接触点在弹丸轴线上的位置位于前定心部中心前方,并且随着弹丸轴线的摆动在小范围内变化。
