基于串并行双分支网络的冲击波信号重构方法
2024-04-11孙传猛陈嘉欣裴东兴马铁华
孙传猛, 陈嘉欣, 原 玥, 裴东兴, 马铁华
(1. 中北大学 省部共建动态测试技术国家重点实验室,太原 030051;2. 中北大学 电气与控制工程学院,太原 030051)
爆炸冲击波[1]对有生目标的毁伤,是超压峰值、比冲量、正压作用时间等特征参量[2]综合作用的结果。准确采集冲击波信号的瞬态信息,是武器威力以及目标毁伤评估的重要途径。然而,受爆炸场空间以及试验成本限制,往往只能在特定角度、有限距离内布置有限数量的测压装置(如图1所示),捕获的数据十分稀疏。此外,当进行冲击波超压测试时,破片击中、电磁干扰、高温环境等恶劣状况,极易造成瞬态信号采集终止,使得采集的信号不完整,出现残缺现象(如图2所示)。显然,深入研究爆炸冲击波信号重构技术,通过有限测点数据重建冲击波场内压力分布、通过残缺数据重构完整的冲击波压力曲线,对武器威力以及目标毁伤评估具有重要价值。
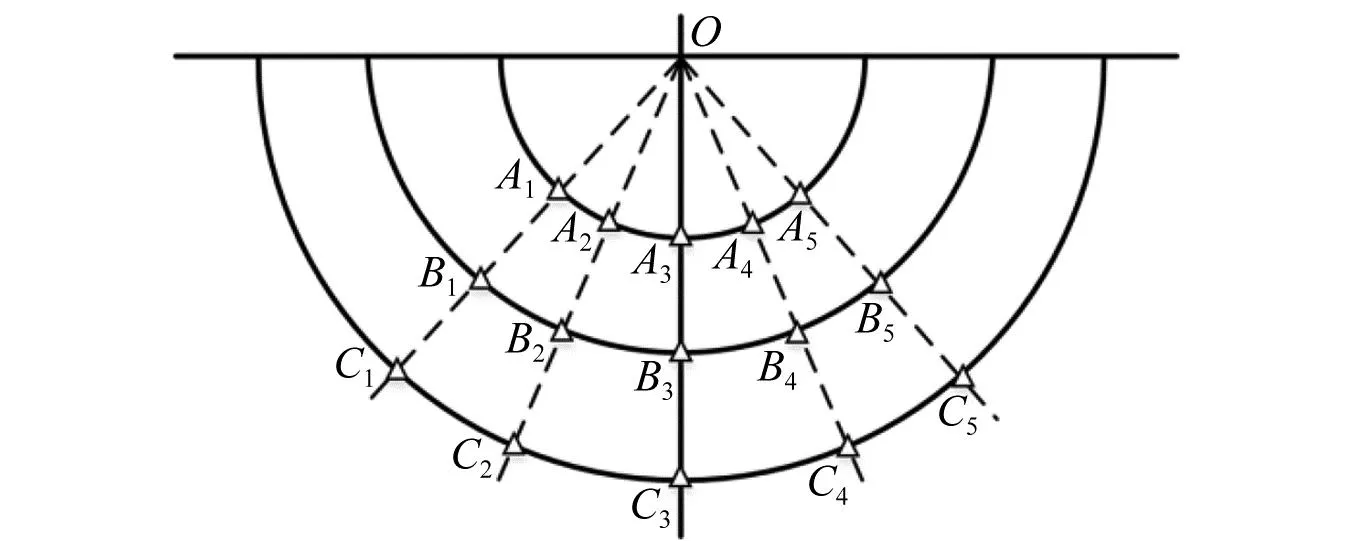
图1 某冲击波超压测试测点布置示意[3]Fig.1 A shock wave overpressure test measurement point arrangement schematic
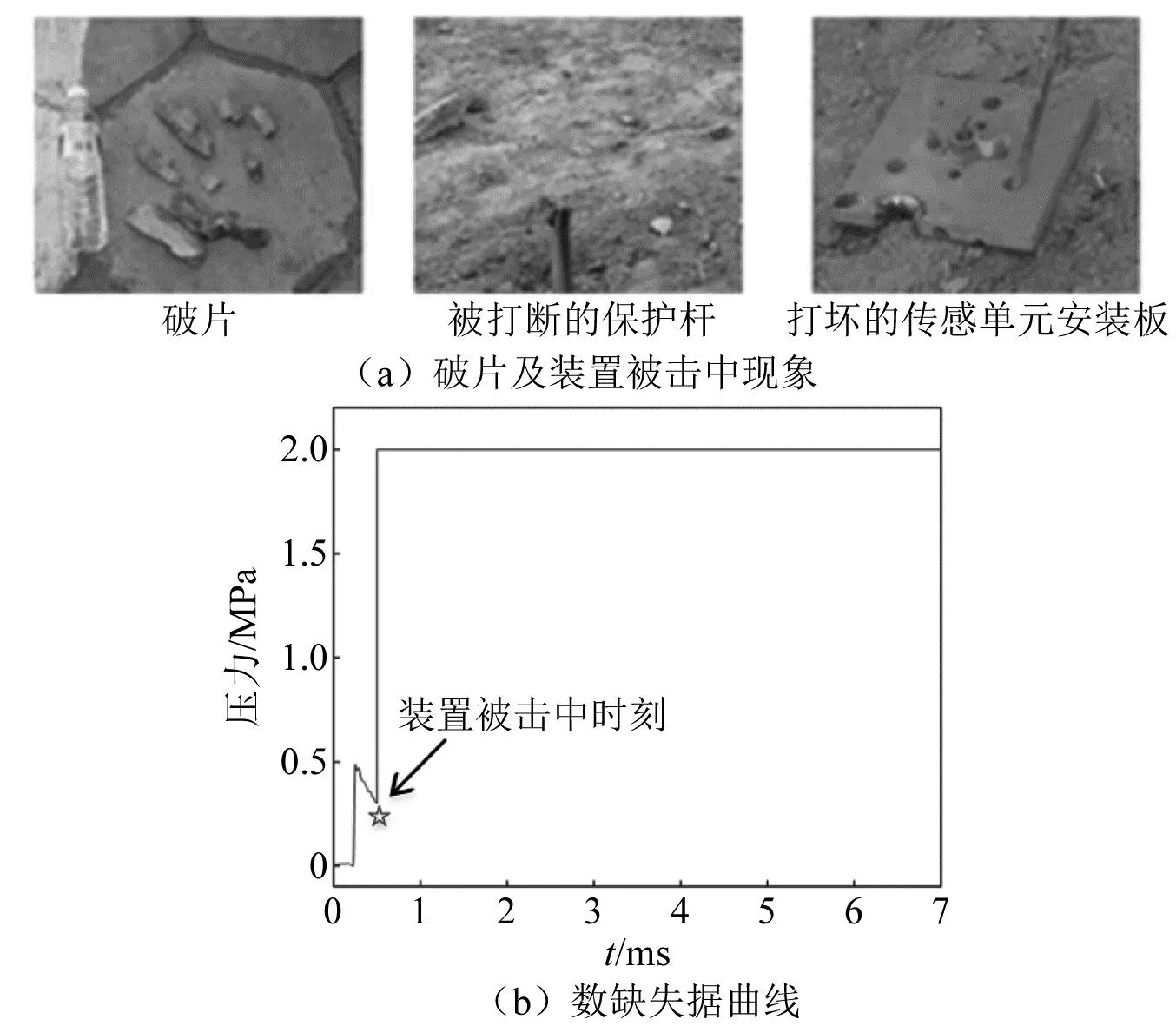
图2 某冲击波测试曲线Fig.2 A curve of a shockwave test
冲击波超压场重建方法主要包含两种:第一种是射线追踪方法[4]、走时线性插值法[5]、反相射线追踪的走时线性插值法[6]、基于广义逆算法改进的射线追踪方法[7-11]等借鉴地球物理结构的方法;上述诸方法受测点数量少、射线路径弯曲等因素影响,重建效果不够理想。第二种是基于统计数据的冲击波重建算法,包括以测点超压峰值进行B样条插值法[12]、基于迭代的几何基的平面和空间三次均匀B样条曲线插值法[13]、基于非均匀有理B样条蛛网插值算法[14]、基于先验信息的EM(expectation maximization)反演算法[15]、基于Zipple算法和高斯牛顿算法[16]以及三次样条插值算法、Biharmonic样条曲面插值算法和径向基函数网络插值算法[17]等;这些方法单纯地使用完全相同的统计值或假设两测量值间数据服从某种分布进而填充所有缺失数据可能是过于武断的。
冲击波残缺信号重构技术则多关注于压缩感知方法。将压缩感知理论[18-23]应用于冲击波信号重构中往往面临苛刻的限制条件:稀疏矩阵选取必须合适;稀疏矩阵、观测矩阵必须不相关;信号需满足联合稀疏先验性等。基于机器学习[24]的信号重构方法是另一种可行方法,使用机器学习算法拟合整个训练数据集的分布,以缺失值周围数据的属性值和整个数据集整体分布来定制生成重构值[25-26]。但是,机器学习算法没有考虑数据集中的时序关系,难以学习时序数据的时间先后关系与数据变化规律。此外,采用平均值、中位数、众数等统计数据来填充信号缺失值[27],也是应用较多的信号重构方法,但存在假设过于武断等问题。
深度学习是对数据特征由低层到高层的逐步抽象和概念化过程,是一种自主学习识别方法,可以敏锐地捕捉信号高阶特征信息[28],为冲击波信号重构提供了潜在有效手段。然而,目前利用深度学习进行信号重构的研究较少,典型如王旭磊、王鑫[29]、罗永洪[30]利用生成对抗网络对时序数据缺失值填充进行了探索性研究,然而生成对抗网络存在难以训练的问题,生成器和判别器在不断博弈中达到均衡,过久的博弈过程可能会使生成器开始退化,总是生成相同的样本点而无法继续学习,这对于信号重构研究而言是难以控制的;豆佳敏[31]利用深度学习技术对冲击波信号压缩感知方法进行了探索性研究,该方法不需要大量数据对网络模型进行训练,而是对每一个信号进行单独学习,进而实现端到端的恢复,规避了稀疏矩阵的设计环节,但该方法仍受限于压缩感知方法,难以学习数据中潜在的高阶特征;孙传猛等利用一维卷积神经网络(convolutional neural networks, CNN)结合BiLSTM(bi-directional long short-term memory)模型对数据特征进行上采样实现冲击波信号的重构,该方法是一种基于端到端的深度学习方法,综合考量了信号的时序关系、频谱特征、数据变化规律等特征信息,并在此基础上对数据特征逐步抽象和概念化,从而自主学习信号中的高阶特征信息。
综上所述,目前爆炸冲击波信号重构技术还存在诸多问题:①相关研究着重于局部特征(如超压峰值)的分析,往往忽视了全局特性对冲击波信号重构的影响;②已有重构技术对深度学习捕捉高阶特征的能力利用不够充分,仅建立了较为简单的非线性映射关系;③已有重构技术缺少对信号时序特征和全局依赖关系的表征,难以掌握复杂的信号本征规律。因此,本文利用Res-GRU模块捕捉冲击波超压信号时序依赖关系等局部特征,利用Trans模块捕捉信号全局潜在特征,提出高阶特征融合机制实现不同阶段信息逐层互补,进而形成基于串并行双分支网络(简记为G-TNet)的冲击波信号重构技术。最后,利用模拟信号和实测信号开展冲击波信号重构试验研究,验证本文方法的有效性和优越性。研究结果对爆炸冲击波信号重构具有重要指导意义。
1 本文方法
1.1 串并行双分支网络(G-TNet)
在冲击波信号重构过程中,无论是射线追踪方法、统计数据方法,还是压缩感知方法、机器学习方法,抑或当前热门的深度学习方法,本质上都是利用某种“特征表示”来表征信号的本征特征进而进行信号填充或预测;不同在于该“特征表示”是人为设计的(传统的射线追踪方法、统计数据方法、压缩感知方法、机器学习方法等诸方法),还是通过模型自动学习的(深度学习方法)。
对于冲击波信号而言,无论峰值压力高低、持续时间长短、噪声干扰强弱,其本质都是一种在连续介质中传播的力学参量发生阶跃的扰动,是理想冲击波信号(如图3所示)对不同测试对象与环境的差异化表现。根据通用近似定理[32-33],一定存在某种深度学习网络,能够通过由底层到高层逐步抽象和概念化冲击波信号特征,从而自动学习到其语义特征(本征特征)。而现有技术方案难以有效应对冲击波超压场综合性不利因素的挑战的主要原因在于,其特征表示要么是浅层的,不属于语义特征(对传统方法而言);要么是自动学习到的语义特征表示不够准确(对深度学习方法而言),进行信号填充或预测时造成较大误差。
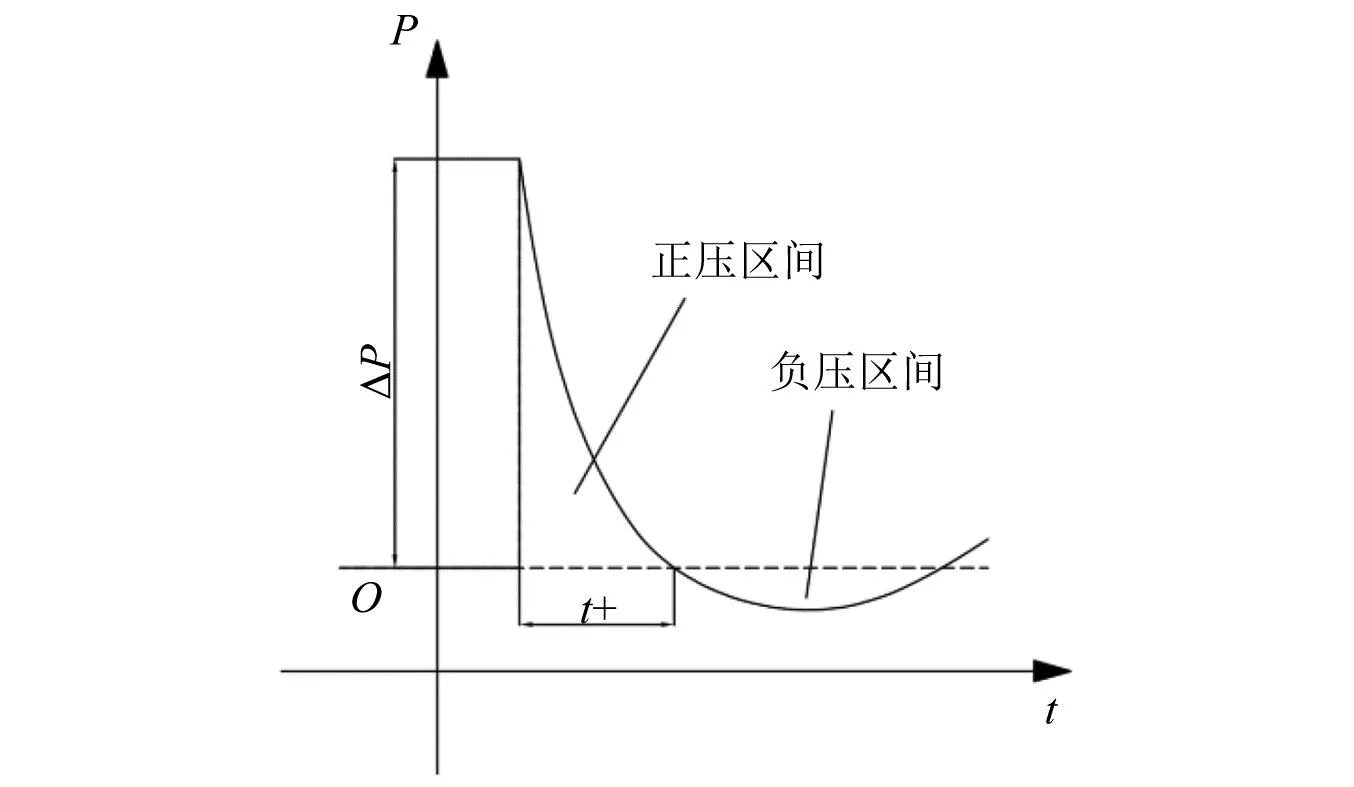
图3 理想冲击波时域波形Fig.3 The ideal time domain waveform of shock wave
显然,冲击波超压场信号重构的难点在于:如何构建一种能有效表征冲击波信号语义特征的深度学习模型,以及如何实现局部时序依赖关系与全局潜在特征之间的平衡。这里的“局部时序依赖关系”是指信号的时序数据的时间先后关系与数据变化规律,这是基于邻域的、局部的聚焦性特征信息;而“全局潜在特征”是指各聚焦性特征之间的长距离依赖关系,是充分地利用“上下文”信息、建立在信号全局理解基础之上的特征信息。
利用深度学习技术进行序列数据处理时有串行与并行两种重要的处理方式。串行方式是指输入序列的每个元素都依次被处理,并将前一个元素的状态作为后一个元素的输入。典型的如循环神经网络(recurrent neural network, RNN),t时刻的输出依赖t-1 时刻的计算结果。串行方式能够适应于某一事物随时间的变化状态或程度,加强前后数据的关联性。显然,利用串行方式十分有利于时序依赖关系等局部特征的提取。并行方式则不依赖数据输入的先后顺序,典型的如Transformer模型。通过自注意力机制,Transformer模型可以同时处理整个序列,而无需像传统的序列模型一样依次处理每个元素。Transformer模型可以实现完全并行的计算,更好地捕捉长距离的依赖关系,计算全局的依赖关系,更容易地解释预测结果,处理不定长序列。值得注意的是,RNN在学习过程中由于梯度消失或爆炸问题,很难建模长时间间隔的状态之间的依赖关系,即长程依赖问题;门限循环单元(gated recurrent unit,GRU)引入更新门和重置门等门控机制来控制信息的累积速度,有助于解决长程依赖问题。
因此,针对爆炸冲击波信号重构问题,本文提出了一个基于GRU和Transformer模型的串并行双分支网络(简记为G-TNet)。G-TNet结构如图4(a)所示,由Embedding层、双分支结构、用于耦合分支的特征融合单元(feature merging unit,FMU)和用于输出的线性层所组成。其中:
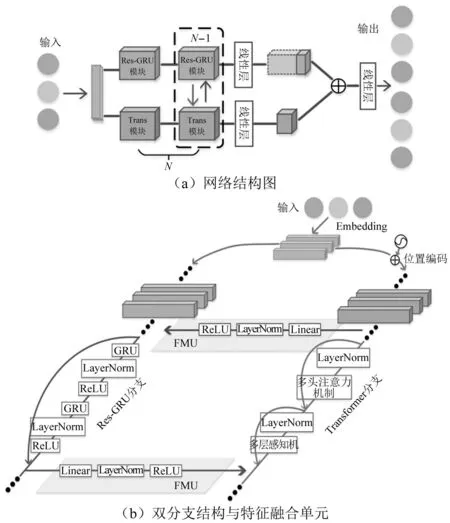
图4 G-TNet网络结构Fig.4 G-TNet model structure
(1) 鉴于冲击波测试过程中采样率、比例距离、测点位置、信号残缺与否等不同导致的信号长度差异,G-TNet使用Embedding层来创建一个低维稠密向量以适应不同长度的输入数据。经过Embedding层后每一输入数据具有了相同维度的向量表示,其输出结果可直接由Res-GRU分支进行处理,而对于Transformer分支对输入数据并行处理的要求,则需增加位置编码来区分冲击波信号中相同数据所处的不同位置。
(2) 双分支结构分为Res-GRU分支和Transformer分支。Res-GRU分支以串行方式捕捉冲击波超压信号时序依赖关系等局部特征,Transformer分支以并行方式捕捉信号潜在全局特征。G-TNet考虑到两种特征的差异性与互补性,将全局上下文信息从Transformer分支逐渐传递至Res-GRU分支的特征映射中,以增强该分支的全局感知能力。同样,Res-GRU分支所产生的局部特征信息也反馈到Transformer分支的特征映射中,以丰富该分支的局部细节信息。而FMU持续的融合特征实现了两种信息的互补,如图4(b)所示。
(3) 在双分支结构中,Res-GRU分支与Transformer分支均由N个重复的Res-GRU模块和Trans模块组成。输入信号经Embedding层后,首先经过一个Res-GRU模块和Trans模块提取初始特征;然后,FMU从第二个Res-GRU模块和Trans模块开始应用,连接Res-GRU分支中的局部特征和Transformer分支中的全局表示。这样,G-TNet的双分支结构可以最大限度地保留局部特征和全局特征,而FMU作为连接分支,在不同阶段充分融合局部与全局特征,实现高阶语义信息互补。
1.2 Res-GRU模块
Res-GRU模块结构如图5(a)所示,包含了两组GRU层、激活函数层和用于归一化特征的LayerNorm层,并在每两组网络之间增加一个捷径连接。GRU层为一个门控循环单元,结构如图5(b)所示,利用更新门和重置门机制,有选择性地增加新的信息和有选择性地遗忘已有累积信息,即
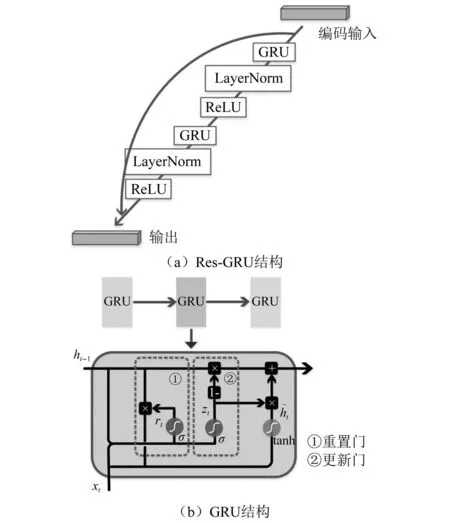
图5 Res-GRU模块Fig.5 Res-GRU block
(1)
式中:ht为GRU层当前时刻t的输出;zt为更新门
zt=σ(Wzhht-1+Wzxxt)
(2)
式中:xt为GRU层当前时刻t的输入;σ(·)为Logistic函数;Wzh和Wzx为更新门相关连接权重。
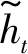
(3)
rt=σ(Wrhht-1+Wrxxt)
(4)
式中: tanh(·)为Tanh激活函数;Wrh和Wrx为重置门相关的连接权重。
Res-GRU模块的捷径连接是极为必要的。G-TNet共包含N个串联的Res-GRU模块,网络层数是非常深的。G-TNet这种较深的网络设计,一方面有助于高阶特征的进一步抽象,使其进一步接近语义特征;而另一方面在学习过程中利用误差反向传播算法更新权重时存在着较大的梯度消失风险。捷径连接将Res-GRU分支网络近似逼近原始目标函数转换为近似逼近残差函数,而在实际中后者更容易学习[34]:①Res-GRU分支可能存在冗余,而捷径连接的恒等映射机制保证经过该恒等层的输入和输出完全相同,解决了网络深度冗余造成的模型性能退化现象;②在网络输出中增加了输入项x,在利用误差反向传播算法更新权重时,该网络对x求偏导时会增加值为1的常数项,使得梯度连乘不会造成梯度消失。
1.3 Trans模块
Trans模块主要借鉴Transformer的编码块结构,依次由LayerNorm层(用于归一化特征)、Multi-head Self-attention 层(多头自注意力机制)、LayerNorm层、多层感知机构成,并在每个LayerNorm层之前增加一个捷径连接,如图6(a)所示。Multi-head Self-attention 会并行地计算多个不同参数的self-attention值,并将各个self-attention 值拼接作为后续网络的输入。其中,self-attention 值计算通常采用QKV模式,如图6(b)所示。
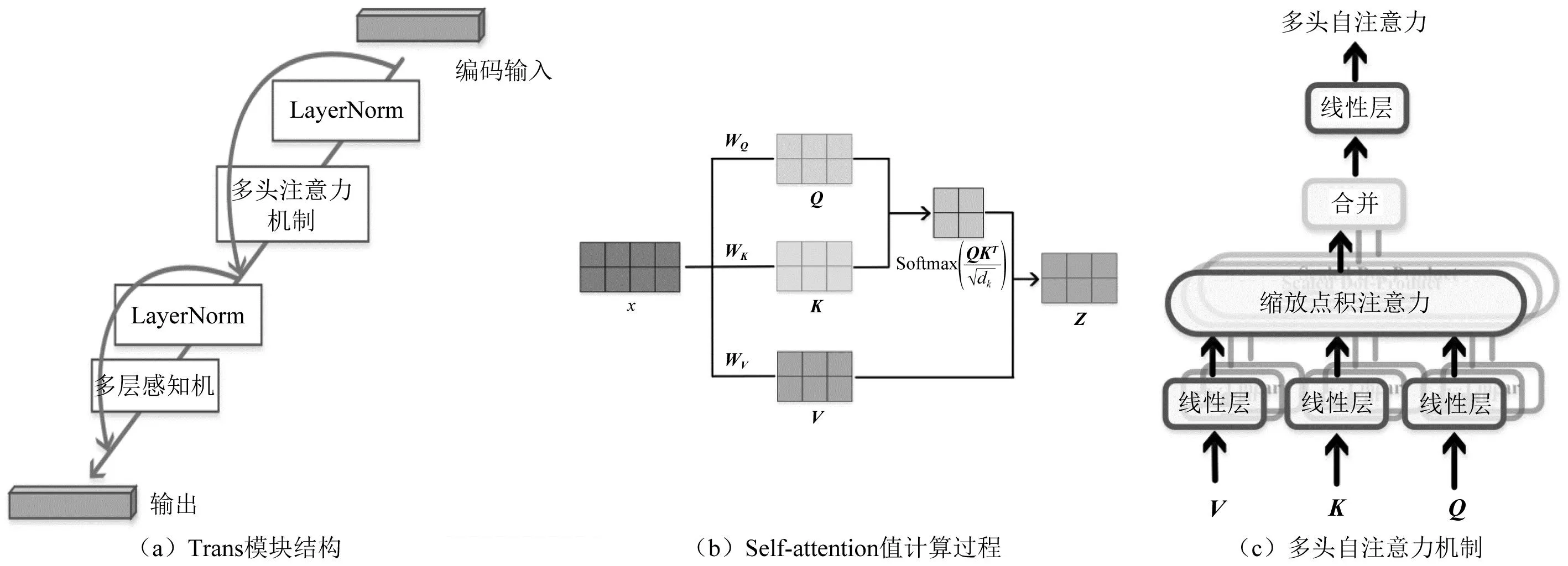
图6 Trans模块与多头自注意力机制Fig.6 Trans block &Multi-head Self-attention mechanism
(1) 首先,将输入数据X经线性映射分别获得Q、K、V矩阵
(5)
式中,WQ、WK和WV分别为线性映射的参数矩阵。
(2) 然后,计算对序列中不同数据的关注程度Score
(6)
式中,dk为K的维度。
(3) 最后,使用缩放点积方法获得最终的self-attention值Z
Z=Softmax(Score)·V
(7)
对于Multi-head Self-attention机制,则使用多组权重值来转换不同的Q、K、V矩阵分别计算相应的自注意力值Z,最终将Z矩阵进行拼接,如图6(c)所示。Multi-head Self-attention通过Q去查询K当中比较重要的信息,得到相应的权重矩阵,再乘以V,让V去关注更重要的信息,忽略更不重要的信息。这样,Multi-head Self-attention机制可以从输入的冲击波信号中,有选择地筛选出少量重要信息并聚焦到这些少量重要信息上,而忽略大多不重要的信息。
同样,Trans模块的捷径连接也起着防止梯度消失和模型退化的作用。值得注意的是,GRU等前述串行网络本身就是一种顺序结构,天生包含了冲击波信号各数据的位置信息;而Trans模块对数据处理采用的是并行方式,即同一个冲击波信号的所有数据一起输入到网络中进行并行训练。这种并行训练方式丢失了每个数据在冲击波信号中的位置信息,这对冲击波信号重构而言是不可接受的。一种行之有效的办法是对输入的数据进行位置编码,以区分相同数据在信号中的不同位置。在冲击波信号重构网络训练中,对Trans模块采用正余弦编码方式,如式(8)、式(9)所示。
PE(pos,2i)=sin(pos/10 0002i/dmodel)
(8)
PE(pos,2i+1)=cos(pos/10 0002i/dmodel)
(9)
式中:PE为位置编码;pos为前数据所处位置;dmodel为Embedding层的向量长度;i的取值范围为0,1,…,dmodel。
1.4 特征融合单元
Res-GRU模块按照串行的方式依次对信号的数据进行处理,利用过去的隐藏状态来捕获对先前数据的依赖性,保留了冲击波信号局部时序依赖关系;而Trans模块利用Multi-head Self-attention机制作为网络的特征提取器,将信号作为整体处理,不依赖于过去的隐藏状态来捕获对先前数据的依赖性,从而允许并行计算,并减少由于长期依赖性而导致的性能下降。
可见,基于Res-GRU模块的Res-GRU分支与基于Trans模块的Transformer分支,分别利用串、并行方式提取了局部与全局等不同形式的信号语义特征,而这些语义特征是可能存在错位风险的。因此,需要添加特征融合单元以消除语义特征错位。本文构建了如图4(a)所示的FMU,以互补交互的方式将局部信息和全局表示连续耦合。由Res-GRU模块和Trans模块性质可知,通过设定其模型节点数和Embedding层输出大小则可控制中间层特征映射大小。因此,本文设定相同大小的向量长度以方便两种信息融合。在G-TNet网络中,从Res-GRU分支(Transformer分支)的第二个Res-GRU模块(Trans模块)开始使用FMU来消除语义特征错位,在线性层、LayerNorm层和激活函数层分别对特征进行对齐,逐步填补各自分支的语义空白。
2 试验研究
2.1 试验方案
首先,建立冲击波信号数据集,由两部分构成:①根据经验公式生成的模拟信号(其时序长度为1 000,混杂有均值为0、方差为0.001的高斯噪声);②实测的冲击波超压信号。
然后,将数据集分为训练集和测试集。利用训练集完成重构模型对冲击波信号特征的学习;利用测试集检验爆炸冲击波信号重构模型的性能。
最后,基于本文所提G-TNet模型分别进行针对有限测点数据的冲击波超压信号重构试验和针对残缺数据的冲击波超压信号重构试验;通过与最新的典型重构方法(GAN-GRU、BiLSTM[35]和CNN-BiLSTM方法)对比,并设置不同的消融试验,以验证本文方法的有效性和优越性。
2.2 试验环境及超参数设置
本次试验的硬件环境:Intel Xeon Gold 5218R CPU,256 GB内存,Nvidia RTX A6000 GPU 48 GB。软件环境:操作系统为64位的Window10,开发环境是Pycharm 2022.2.3,开发语言为Python3.7.0+PyTorch1.7。
本次对比试验及消融试验设置相同的超参数:采用Adam优化器,初始学习率为0.001,共训练60个Epochs,学习率分别在第30个和第50个Epochs处衰减0.5倍。Embedding层输出向量长度为128,Trans模块中heads设置为6。损失函数采用L1+L2损失。对于GAN-GRU模型,考虑其训练方式不同,设置迭代次数为200个Epochs。
2.3 评价指标
考虑到冲击波超压信号通常以超压峰值、正压作用时间、比冲量作为毁伤威力的考核指标,本文选择均方误差(mean square error, MSE)、平均绝对误差(mean absolute error,MAE)、平均峰值误差、平均正压时间误差和平均比冲量误差作为模型输出结果的评价指标。
(1) MSE反映真实值与重构值之间差异平方的平均。
(2) MAE反映真实值与重构值之间差异绝对值的平均。
(3) 平均峰值误差(EP),反映冲击波真实信号与重构信号之间超压峰值相对误差的平均值
(10)
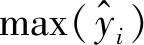
(4) 平均正压时间误差(ET),反映冲击波真实信号与重构信号之间正压时间的相对误差平均值
(11)
式中:X为正压区间的横坐标值;XMAX、XMIN分别为正压区间的终点和起点;
(5) 平均比冲量误差(ES),反映冲击波真实信号与重构信号之间比冲量的相对误差平均值
(12)
(13)
式中:M为冲击波信号正压区间的长度;S为冲击波信号的比冲量。
2.4 结果与讨论
2.4.1 针对有限测点数据的冲击波信号重构试验
(1) 模拟冲击波信号重构试验结果与讨论
针对有限测点数据的模拟冲击波信号重构试验,模型的输入数据为不同测点与爆炸中心的比例距离值,输出结果为重构的冲击波信号,结果如图7(因篇幅有限,仅展示部分数据)与表1所示。在图7中,原始冲击波信号为深色,重构冲击波信号为浅色(下同);表1中: Parameters与FLOPs分别为深度学习网络模型的参数量和计算量; 加粗数字表示相应指标下的最优值(下同)。

表1 模拟冲击波信号的冲击波场压力分布重构试验结果Tab.1 Experimental results of reconstructing pressure distribution in shock wave field by simulating shock wave signal
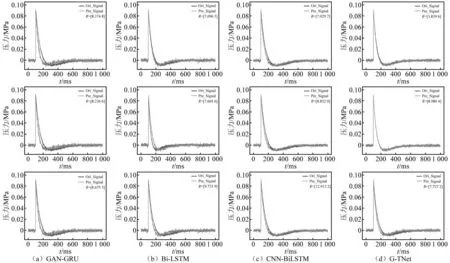
图7 模拟冲击波信号的场压力分布重构结果Fig.7 Reconstruction results of field pressure distribution of simulated shock wave signals
由图7可知: GAN-GRU、BiLSTM、CNN-BiLSTM和G-TNet(本文方法)均得到了较为理想的重构结果,而G-TNet重构曲线与原始曲线贴合最为紧密,表明G-TNet对冲击波语义特征的捕捉能力最强,重构的冲击波曲线最为准确。由表1可知:G-TNet重构信号的MSE、MAE、平均峰值误差(EP)、平均正压时间误差(ET)、平均比冲量误差(ES)均为最低值,取得了最优结果;G-TNet重构信号平均峰值误差(EP)、平均正压时间误差(ET)、平均比冲量误差(ES)分别为0.49%、15.62%、17.66%,满足冲击波场压力重构指标要求;G-TNet模型的参数量和计算量分别为6.65 MB和6.66 MB,在时间复杂度、空间复杂度方面取得了较好的平衡。这表明G-TNet能够较好地实现不同测点位置的冲击波信号重构。
(2) 实测冲击波信号重构试验结果与讨论
针对有限测点数据的实测冲击波信号重构试验结果如图8(因篇幅有限,仅展示部分数据)与表2所示。由图8可知:当输入数据的特征较多时,GAN-GRU难以收敛,而BiLSTM、CNN-BiLSTM和G-TNet均实现了信号重构;而G-TNet重构曲线与原始实测曲线贴合最为紧密。由表2可知,G-TNet重构信号的MSE、MAE、平均峰值误差(EP)、平均正压时间误差(ET)、平均比冲量误差(ES)均为最低值,取得了最优结果;G-TNet重构信号平均峰值误差(EP)、平均正压时间误差(ET)、平均比冲量误差(ES)分别为27.01%、15.91%、19.33%,满足冲击波场压力重构指标要求;G-TNet模型的参数量和计算量分别为31.43 MB和31.44 MB,在时间复杂度、空间复杂度上也较为平衡。这表明G-TNet对实测信号重构仍具有良好的适应性,能够较好地实现不同测点位置的冲击波信号重构。
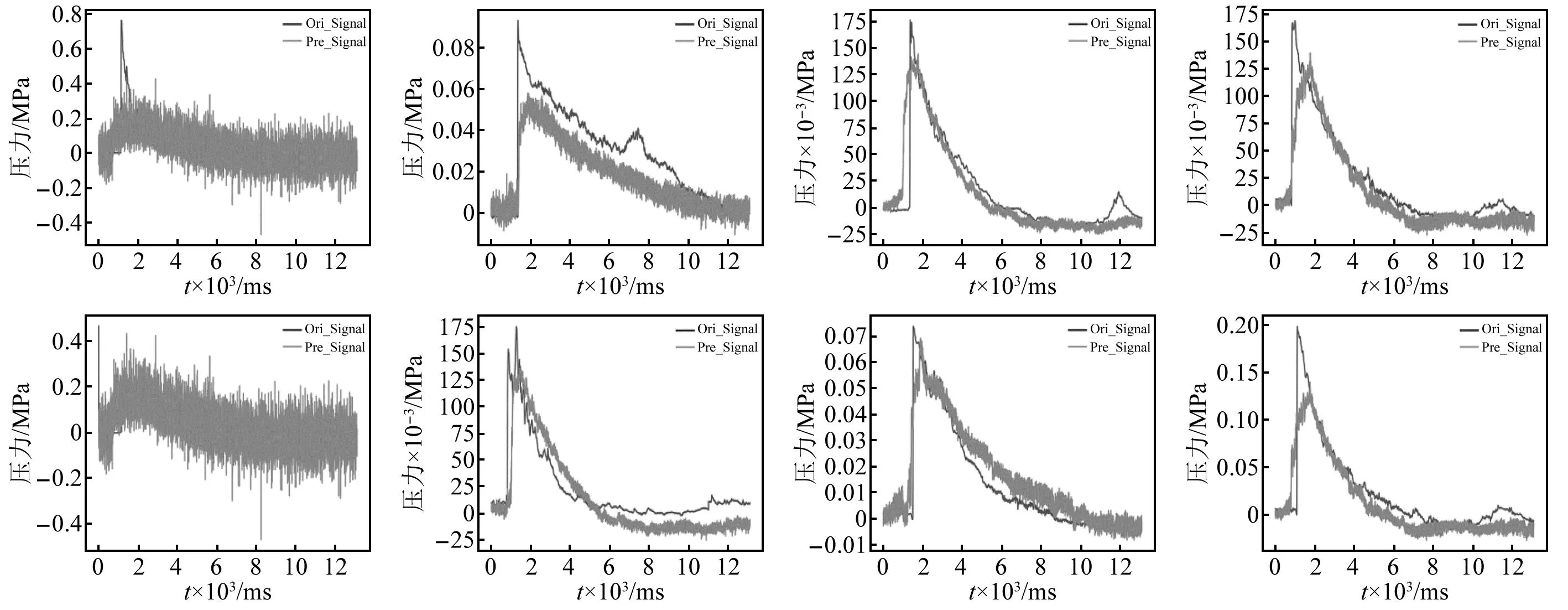
图8 实测冲击波信号的场压力分布重构结果Fig.8 Reconstruction results of the field pressure distribution of the measured shock wave signal
2.4.2 针对残缺数据的冲击波超压信号重构试验
(1) 模拟冲击波信号重构试验结果与讨论
将模拟的残缺数据冲击波信号测试数据输入到训练好的爆炸冲击波信号重构模型中,对残缺信号进行重构以期获得完整的冲击波信号。冲击波残缺曲线重构试验中的输入数据为信号的前半段部分,本文选择时序信号中的前130个数据(即认为在第130个数据点时冲击波信号开始缺失),模型输出结果为重构冲击波信号的后半段部分,试验结果如图9(因篇幅有限,仅展示部分数据)和表3所示。由表3可知,G-TNet相对于其他方法达到了最优结果,MSE为5×10-6、MAE为0.001,对比其他方法有明显提升,该结果表明G-TNet能够较好地实现对冲击波残缺信号的重构。
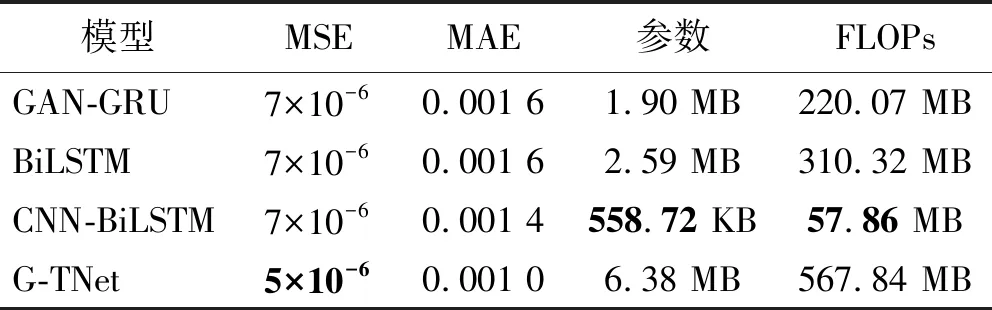
表3 模拟冲击波信号的残缺数据重构试验结果
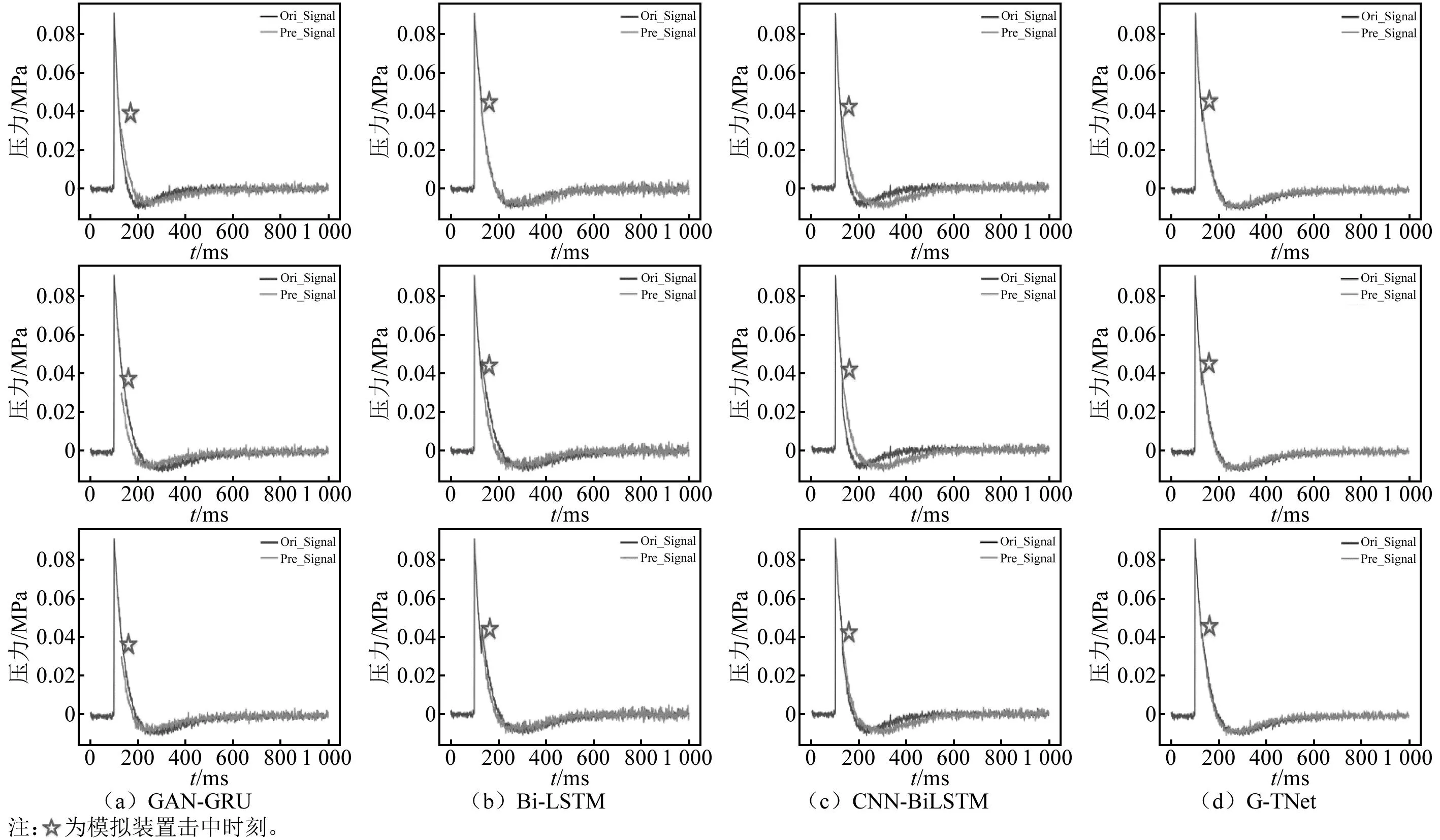
图9 模拟冲击波信号的残缺数据重构结果Fig.9 The results of reconstructing the residual data of the simulated shock wave signals
(2) 实测冲击波信号重构试验结果与讨论
利用实测冲击波信号验证爆炸冲击波信号重构模型,选择前3 000个数据作为模型的输入(即认为在第3 000个数据点时冲击波信号开始缺失),模型输出结果为重构冲击波信号的后半段部分,结果如图10(因篇幅有限,仅展示部分数据)和表4所示。由图10和表4可知, G-TNet 重构信号的MSE和MAE分别为0.000 5和0.017 1,表明G-TNet对实测信号重构仍具有良好的适应性。
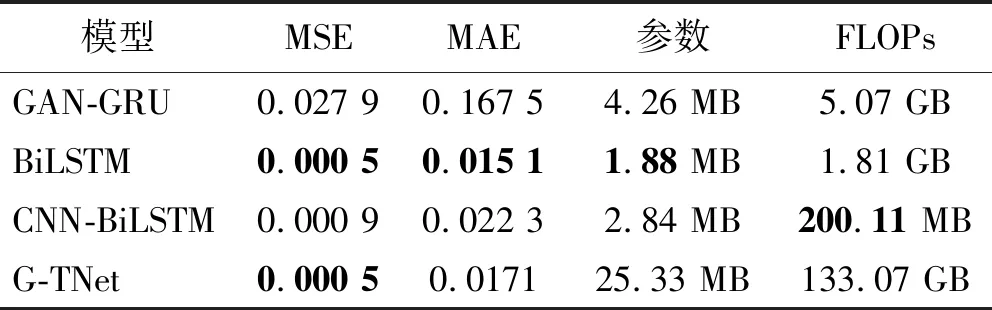
表4 实测冲击波信号的残缺数据重构试验结果
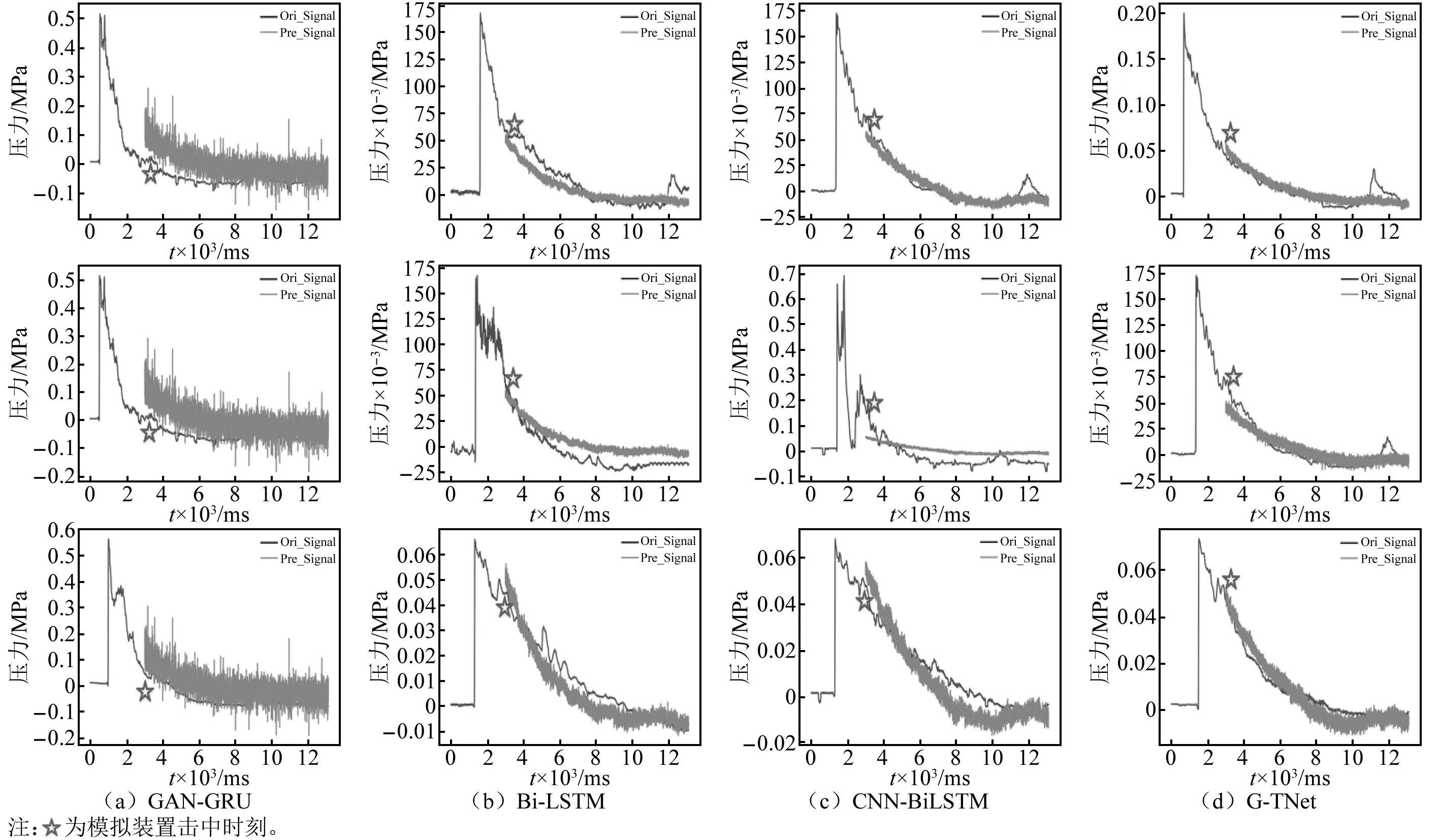
图10 实测冲击波信号的残缺数据重构结果Fig.10 The results of the reconstruction of the residual data of the measured shock wave signal
2.4.3 消融试验
为了进一步分析G-TNet的性能,设置两组消融试验:①屏蔽Res-GRU分支,仅保留Transformer分支,并加深该分支;②屏蔽Transformer分支,仅保留Res-GRU分支,并加深该分支。消融试验结果如表5~表6所示,部分试验图像如图11~图12所示。

表5 模拟冲击波信号重构消融试验结果Tab.5 Test results of simulated shock wave signals reconstruction ablation
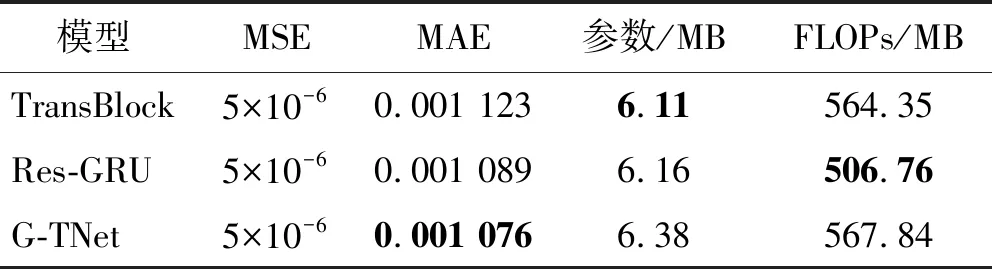
表6 模拟冲击波信号残缺数据重构消融试验结果
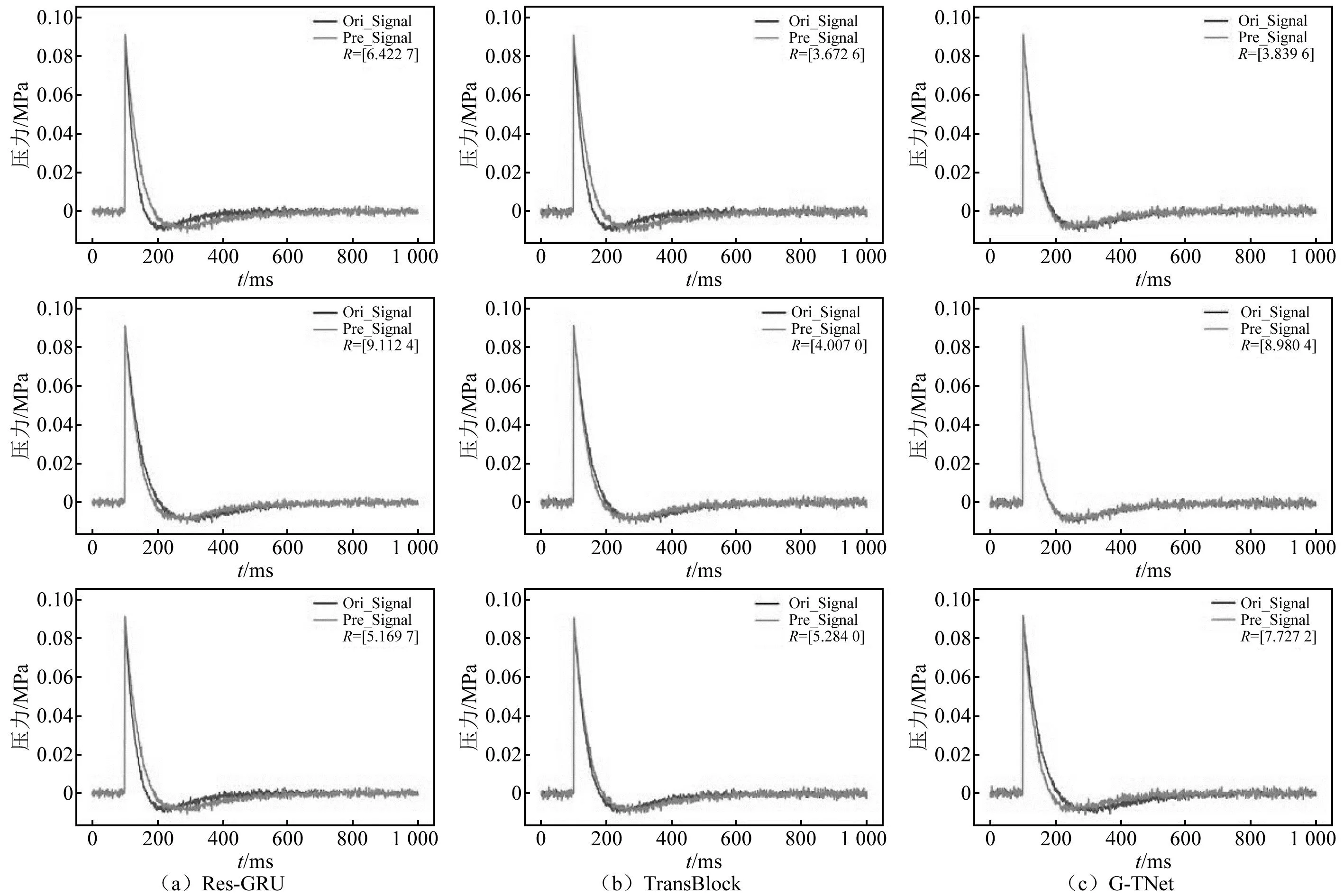
图11 模拟冲击波信号重构消融对比结果Fig.11 Comparison results of simulated shock wave signals reconstruction ablation
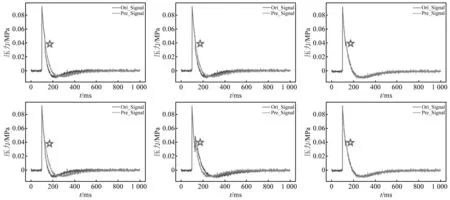
图12 模拟冲击波信号的残缺数据重构消融对比结果Fig.12 Comparison results of reconstructed ablation of residual data from simulated shock wave signals
消融试验结果表明:
(1) 在模型准确度方面,双分支结构与特征融合单元是本文提高模型性能的关键,局部特征和全局信息的融合机制影响最大。
(2) Res-GRU分支所占据的参数量和计算量较少,但由于其串行处理数据的方式,缺少对全局特征的关注,导致了对信号峰值的预测能力较差。
(3) Transformer分支所占据的参数量和计算量与G-TNet相近,其以并行的方式处理数据,缺少对局部特征的关注,导致信号整体拟合效果较差。
综上所述,在参数量和计算量相近的情况下,采用双分支结构,逐层融合Res-GRU分支产生的局部特征和Transformer分支产生的全局信息,能够极大改善单一分支所导致的特征分析不全面问题,且能够满足冲击波超压信号重构的多种指标要求。
3 结 论
(1) G-TNet利用Res-GRU分支以串行方式捕捉冲击波超压信号局部时序依赖关系,利用Transformer分支以并行方式分析信号全局潜在特征,利用特征融合单元进行高阶特征融合,实现不同阶段信息逐层互补,在冲击波信号重构中综合考量了信号的时序关系、数据变化规律等特征信息。
(2) G-TNet在基于有限测点数据的冲击波场压力分布重构试验中,重建的模拟、实测超压数据与原始值之间MSE分别为5.0×10-6、1.2×10-3,平均峰值误差分别为0.49%、27.01%,平均正压时间误差分别为15.62%、15.91%,平均比冲量误差分别为17.66%、19.33%;在基于残缺数据的冲击波压力曲线重构试验中,重构的模拟、实测信号的缺失值与原始值之间MSE分别为5.0×10-6和5.0×10-4,MAE分别为0.001 0和0.017 1;能够满足实际冲击波场压力重构的多种指标要求。
(3) 消融试验表明,G-TNet融合不同分支所产生的全局信息和局部特征可以极大地提升模型性能,且模型的参数量和计算量不会产生过多增加。
