数据驱动的液体火箭发动机健康监测算法研究

刘梓琰,吴毅伟,王冠,李璨,王姝淇,陈海宝

(1. 北京宇航系统工程研究所,100076,北京;2. 上海交通大学电子信息与电气工程学院,200240,上海)

低温液体火箭发动机涡轮泵具有工作转速高、工作环境复杂恶劣的特点,其涡轮受高、低温冲击和高速旋转时产生的离心力、热应力、振动等共同作用,是发动机工程研制中容易出现问题的零部件。特别是在氧涡轮泵中,为减少涡轮端悬臂较长给转子动力学设计带来的影响,氧涡轮盘一般采用轻薄化设计,导致其故障概率进一步增加。因此,有必要开展针对氧涡轮泵故障检测的相关研究,以实现故障的早发现、早定位。

基于数据驱动的故障检测与识别方法与传统的基于传感器信号或物理模型的方法相比,既具备基于传感器信号方法的简单易实现,也具备基于物理模型方法深层次分析能力,并且更为泛化,能够提炼出技术人员建模经验之外的信息[1-3]。目前,数据驱动算法研究的关注越来越高,如支持向量机[4]、贝叶斯分类器[6-7]、极限学习机[8-9]、最近邻分类器[10]、支持矩阵机[11]、随机森林[12]以及最小二乘向量机[13-15]等机器学习算法都在故障检测及诊断领域得到了应用。在发动机故障诊断与检测领域,时域统计学特征、经验模态分解[16]、全局谱分析[13]、快速傅里叶变换[17]、小波变换[4]和离散傅里叶变换[18]等都是常用的特征提取算法。此外,当可提供的数据样本较少时,Li等[19]通过的时频图特征,然后用支持向量机的方法对故障样本和正常样本进行分类,取得了不错的效果。针对振动信号,Harmouche等[16]提出了一种名为全局谱分析的特征提取方法,该方法在预处理阶段对振动信时频转换,分析所有样本号进行包络分析以及快速傅里叶变换,接着利用主频特征选择和主成分分析来提取主特征,最后利用线性判别器完成了故障样本分类。

Mathew等[20]在预处理阶段对采集到的信号进行小波变换并从变换系数中提取故障特征,接着用贝叶斯分类器来对经过主成分分析后的降维特征分类,从而能准确识别故障样本。Georgoulas等[21]提出了一种振动信号特征融合方法以构造新的故障特征。该方法将两个加速器采集到的信号通过协方差矩阵进行特征融合,并将融合信号通过最近邻分类器和主成分分类器进行故障诊断。该方法在对具有多个加速计传感器的系统进行诊断时具有较好的性能。

文献[22]通过阶比分析研究了机动车变速箱齿轮的故障检测技术,该技术融合了时域分析与频域分析,有效提取了变速箱信号的特征,特别是在非均匀工况下,其效果优于单一的频域分析方法。文献[23]针对传统电路故障检测在波形图诊断与实际波动存在偏差以及影响检测准确性的问题,引入了一种结合小波变换和神经网络的新检测技术,此方法能够精确地诊断各类故障状态。文献[24]针对时间序列数据中多元指标众多、时间跨度大导致的特征提取难题,应用主成分分析(PCA)方法提取关键特征,并利用长短期记忆(LSTM)网络减少数据维度,这不仅保持了数据间的相关性,同时也简化了数据结构和模型的复杂度。

考虑大推力氢氧发动机复杂的物理机理与多次试车过程中产生的海量数据,借助机器学习方法实现发动机试车数据异常特征的深度挖掘,构建智能化、高精准的氢氧发动机故障检测与识别工具,绕过物理机理探究异常数据特征,在实现故障发现与识别的基础上反哺技术人员深化故障机理的理解,将是未来很长时间内的重要工程应用方向[25]。

液体火箭发动机的氧涡轮泵是其核心组件,改型发动机在历次试车过程中积累了丰富的试验数据,为数据驱动故障诊断方法的研究提供了有力支撑。本文开展氧涡轮泵试验数据分析与挖掘技术研究,从数据层面出发,对氢氧发动机涡轮泵试验数据进行分析与挖掘,绕过复杂的物理机理,基于速变与缓变数据建立故障检测模型。在此基础上提出一种故障模式判别方法,算法模型框架如图1所示。该模型可以接受多种工况的数据输入,并根据输入类型执行相应算法。

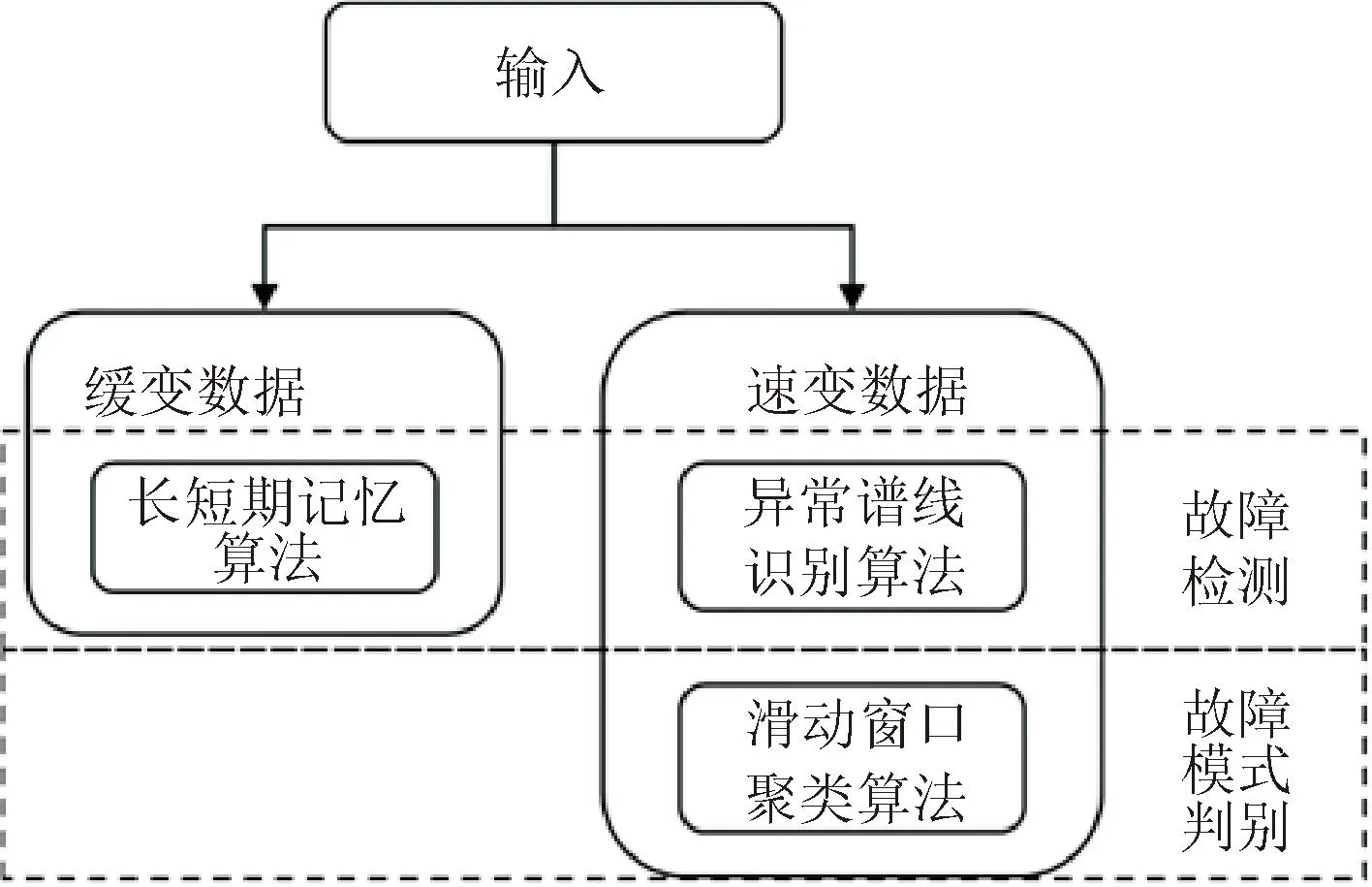
图1 算法模型框架图Fig.1 Algorithm model frame diagram

1 数据描述

本文使用某型液体火箭发动机试车数据。该数据从火箭发动机传感器收集得来,均为时序数据,同时包含高频采样样本和低频采样样本。全部试车数据覆盖共计18台发动机、56次试车试验,即56个时间序列。每次试车提供一个包含大量测量参数的数据集,每个序列采样长度为几万到几十万不等,在建模过程中进行数据重构以满足输入要求。参数可分类为缓变数据(如氧涡轮出口压力、燃气发生器室压等)、速变数据(如氧涡轮轴向振动、氧泵轴向振动等)。各次试车的基本状态统计如表1所示,其中试验编号方式为发动机编号-该发动机试车次数,如9-1代表9号发动机第一次试车(后文对发动机统一表述为xx号发动机,对试车试验统一表述为xx-yy次试车)。

表1 历史试车发次状态Table 1 Historical test run status

其中未特别标明状况的氧转子视为正常。第8号发动机试车数据较为特殊,由于8-1次试车出现R5裂纹,该发动机经过修理后继续进行8-2以及8-3 次试车。烧蚀、R0.2、R1.2、R3、R4、R5裂纹为氧转子不同的故障模式,表征裂纹在轴盘上的不同位置。值得指出,R1.2、R3、R4故障模式由于负样本数量较少,因此本文后续故障模式判别算法中主要针对R0.2、R5两种故障模式进行算法设计和实现。

发动机试车数据集中包含大量状态参数,这些参数往往不是相互独立,每个参数对于故障的表征能力也强弱不一,若向模型输入全部参数,不但会导致运算效率低下,还会影响模型的准确性与鲁棒性,影响最终算法效果。因此,在构建并训练算法模型前,有必要对试车数据集中状态参数进行筛选。采用信息熵分析、主成分分析等统计分析方法,分别对速变参数与缓变参数进行重要性排序。

与故障特征相关性较强的速变参数如表2所示,速变参数均为振动参数,采样频率高达50 kHz。整体呈现出剧烈波动以及非平稳性,因此在频域中分析振动数据较为合适。与故障特征相关性较强的缓变参数如表3所示,均为燃气路数据,包括温度参数与压力参数等。燃气炉数据相对平稳,只在部分时间点会出现跳变。

表2 重要速变参数Table 2 Important fast-varying parameter

表3 重要缓变参数Table 3 Important slow-varying parameter

2 基于速变数据的横向降噪图像处理算法

速变参数的采样频率高达50 kHz,从频域入手更易抓取故障现象的数据特征,而时域则可反应发动机工作状态的变化情况,因此考虑构建时频谱图表征完整试车工况下的数据特征。在以60 ms窗口对氧泵以及氧涡轮进气壳体组件的轴径切向振动参数进行时域切片并经过短时傅立叶变换处理后进行拼接,可得振动参数的时频谱图,16-6次试车的氧涡轮进气壳体组件轴向振动参数的时频谱图如图2所示,16-1次试车的氧涡轮进气壳体组件轴向振动参数的时频谱图如图3所示。图中横坐标代表频域,范围为4.5～5.5 kHz,纵坐标代表时域,范围为该发次试车的时间,亮度代表振动的能量。除上述两次试车之外,观察多个试车发次,发现在氧涡轮进气壳体组件轴向振动参数的时频谱图中普遍存在以下情况:正常发次在5 kHz频段附近存在高亮竖纹,而故障发次在该频段区域额外出现高亮斜纹。因此,可以将该参数时频谱图中斜纹作的出现与否作为判断发动机氧涡轮泵健康状态的判据。基于此,本节提出一种基于图像识别的发动机氧涡轮泵故障检测方法。

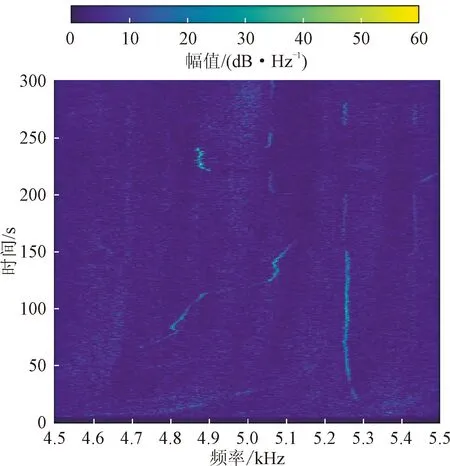
图2 16-6次试车氧涡轮进气壳体组件轴向振动参数时频谱图Fig.2 Time-frequency spectrum diagram of axial vibration parameters of oxygen turbine intake housing assembly of 16-6

图3 16-1次试车氧涡轮进气壳体组件轴向振动参数时频谱图Fig.3 Time-frequency spectrum diagram of axial vibration parameters of oxygen turbine intake housing assembly of 16-1

2.1 算法模型

图像识别的流程如图4所示,首先聚焦斜纹出现区域,将时频谱图截取成为439×376=165 064像素大小,然后将时频谱图灰度化。此时图中不仅存在明亮竖纹与斜纹,还存在背景噪声。针对这一特点,本文提出一种横向降噪方法,首先计算时频谱图每一时刻在所有频率上的像素值均值,然后对每个像素值减去该像素值所在时刻的像素值均值,计算公式为

图4 斜纹图像识别流程图Fig.4 Twill image recognition flow chart

式中:G(t,f)为横向降噪后时刻t、频率f上的像素值;g(t,f)为横向降噪前时刻t、频率f上的像素值;F为时刻t上所有频率的像素点数。由图4降噪效果可以看出,横向降噪法可以在最小程度不影响谱线的情况下,有效减少由于传感器故障造成的异常噪声,减少对后续谱线分析的干扰。在缓解了由于传感器故障所造成异常噪声的影响,需要进一步增强谱线亮度,减少噪声像素点的亮度。由于时频谱图在经过横向降噪和边缘分析等图像处理过程后,图像整体显示较暗,图像像素值均在0～60的范围内,整体偏低,为了进一步放大明暗的差异,本文采用提亮法等比提高图像的像素值,计算公式为

式中:G(t,f)为横向提亮后时刻t、频率f上的像素值;g(t,f)为横向提亮前时刻t、频率f上的像素值;min(g)为图像中最暗像素点的像素值;max(g)为图像中最亮像素点的像素值。另外,当时频谱图的谱线较粗时,经过边缘检测算法处理后的谱线在图像上呈现是一圈细线,对于后续判断区分噪声点和谱线会造成干扰,因此采用中值滤波法来模糊图像,填补较粗谱线应边缘分析而导致中空的区域,为后续识别谱线提供助力。最后,经过横向降噪、高斯模糊、边缘分析、提亮、中值滤波等一系列图像处理方法,完成时频谱图的预处理,实现时频谱图的降噪和谱线增强。

由于不同发次的斜纹偏斜角度不同,直接对斜纹进行识别较为困难,因此选择对竖纹进行识别并剔除,再判断剩余亮纹区域的大小,若剩余亮纹大小满足设定阈值,则判定该谱图存在斜纹,即该发次试车中,发动机存在故障。在这一环节中,竖纹判据为偏斜角度小于5°,剔除剩余亮纹为斜纹的判据为存在大于100像素点的亮纹。

2.2 算法步骤

具体算法流程如下:

(1)对时频谱图先后进行灰度化、边缘分析、去噪、二值化处理;

(2)通过基于面积的区域划分选出面积较大的白色区域,而将那些面积较小的区域认为是噪点并去除;

(3)做直纹检测,检测出方向较为竖直的直线并将这些直线经过区域看作正常谱线并去除,经过这些流程后若结果图仍留有白色区域,则认为该时频谱图中存在倾斜的异常谱线。

2.3 测试结果

时频图谱图像识别方法测试结果如表4所示。应用19个试车试验的数据对算法进行了测试,其中6-1,6-2次试车判断错误,而6-6次试车由于存在不明显斜纹导致判断错误,其他均判断正确,总体故障诊断准确率为84.2%。可以认为该算法能够较为准确地检测试车发动机故障。

表4 时频图谱图像识别方法测试结果Table 4 Test results of time-frequency spectrum image recognition method

以往方法如文献[2]中利用图像数据来判别火箭设备寿命,例如利用深度学习方法训练时间相对较久,而本文方法直接从图像本身角度基于斜纹特征先验理论完成故障检测,在一定程度上减少了训练损耗和推理时间,为航天发动机异常检测领域提供了一种新的研究思路。

此外,该算法可计量斜纹的状态特征,如亮度(对应频谱强度),斜率(对应频谱峰值漂移速度),对于不同程度、不同类型的故障,斜纹的表征存在差异,该方法可为技术人员提供更多维度的故障相关信息。

3 基于缓变数据的LSTM自适应阈值算法

基于缓变数据的故障检测方法,往往通过考察数据变化趋势并抓取异常的趋势特征实现。

如表3所示,重要缓变数据均为温度或压力,因此通常二者存在关联。假定在正常工况与故障工况,缓变参数之间的关系存在差异,且正常工况下的参数关系应该是一致的。因此,若找到正常工况下缓变参数间的映射关系,并把这一映射关系带入到故障工况,那么计算值与实际值应该会出现明显偏差,通过对偏差设置阈值的方式,即可判定发动机的健康状态。

缓变数据通常在时域上进行分析,构建缓变数据间的映射关系即处理多变量时间序列数据,LSTM网络常用于时间序列的预测,因此使用LSTM神经网络模型构建参数间映射关系,实现故障检测。

3.1 算法模型

基于LSTM网络的故障检测方法为每一次预测值yh(t)计算预测误差e(t)=|y(t)-yh(t)|,所有的误差形成一个一维向量e=[et-h, ,et-1,et],其中h是用于评估当前误差的历史误差值个数,也可看作窗口长度。然后对误差集e进行平滑处理,以抑制基于LSTM的预测经常出现的误差峰值,使用指数加权平均(EWMA)产生平滑误差。为了评估数值预测结果,需要为它们的平滑预测误差设置一个阈值,阈值ε计算定义为

Δμ(es)=μ(es)-μ({es∈es∣es<ε})

式中:Δμ(es)为序列的整体均值减去该序列中所有非异常值的均值;Δσ(es)为序列标准差与序列中正常值标准差的差值;|ea|为序列中异常值的个数;|Eseq|为拥有连续异常值的异常序列的个数。平滑误差高于阈值的值对应的试车发次被分类为异常。

3.2 算法步骤

算法的流程可以归纳如下:①LSTM网络学习时序数据做预测;②收集每一步的误差构成误差向量;③对误差做加权平均的平滑处理;④根据平滑后的数据计算阈值;⑤平滑误差高于阈值的值对应的试车发次被分类为异常。

3.3 测试结果

下面将LSTM自适应阈值故障检测应用在氧涡轮泵发动机燃气路数据上。燃气路参数分析如下:氧燃气路参数包括燃气发生器室压、燃气喷嘴压力、氧涡轮入口压力、氧涡轮出口压力;网络训练输入参数为燃气发生器室压、燃气喷嘴压力、氧涡轮入口压力,网络训练输出参数为氧涡轮出口压力。

LSTM模型主要由3个LSTM单元以及一个全连接层构成。全连接层最终的输出维度设定是1维。训练过程优化器采用Adam,损失函数为均方误差(MSE),学习率为0.001,训练迭代次数为2个epoch,batch_size设置为32。32车次中6个发次的测试结果如图5所示。

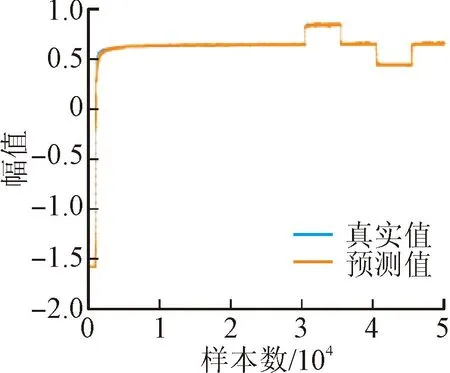
(a)32-1

对16号发动机6次试车数据进行量化分析,从16-1到16-6的幅值误差均值依次为0.010 7、0.009、0.017 2、0.017 5、0.027 5、0.103 3,其中16-5和16-6在LSTM网络预测过程中,就已经出现大量偏离预测值的样本点,所以最终被判断为故障发次,其误差均值高于其他试车发次。缓变数据故障检测方法测试结果如表5所示。

表5 缓变数据故障检测方法测试结果Table 5 Test results of slow variable data fault detection method

测试共覆盖了39次试车,其中6-2发次出现了误判,同时没有检测出7-2发次的故障,故障识别准确率为94.9%。6-5、16-5次试车判断结果与时频谱图图像识别故障检测算法结果一致,因此也可以认定这两个发次虽然未经过拆机检查,但出现故障的可能性非常大,其他发次均判断正确或判断结果合理。

4 基于滑动频率窗口聚类算法的故障模式判别方法

如表1所示,整个、发动机试车数据集内已知的故障模式为烧蚀、R0.2裂纹、R1.2裂纹、R3裂纹、R4裂纹、R5裂纹,表征裂纹在氧涡轮泵轴盘上的不同位置。因此,可在故障检测算法的基础上进一步深入,构建故障模式判别算法。假定不同故障模式均可反应在振动数据的频域特征中,并且不同的故障模式的特征理应有独特的频域区间。在此假设下,选定具备特定故障模式的正常或故障发次数据作为输入,通过频域滑窗穷举频域区间,在每个频域区间中进行聚类分析,找到每个可通过聚类分析区分该发次的故障或健康状态的频域区间,综合频域窗口信息与并针对每类故障模式训练对应的故障模式识别算法。

4.1 算法模型

本算法使用氧涡轮泵轴、径、切向振动数据,整体流程如图6所示。首先选择一组存在特定故障模式与正常工况的试车发次组合,例如6-1至6-4发次(健康)与6-6发次(R0.2裂纹),设定一个宽度为625 Hz的频率窗口初始为0～625 Hz,在此窗口下穷举一个可以区分正常与故障工况的聚类中心,若无法构造满足要求的聚类中心,则滑窗向右滑动625 Hz继续穷举聚类中心,若找到符合要求的聚类中心,则保存该频率窗口以及聚类中心并且滑窗滑动625 Hz,若无法找到符合要求的聚类中心,则直接平移滑窗,直到滑窗遍历整个频域(设置为0～6.25 kHz)。

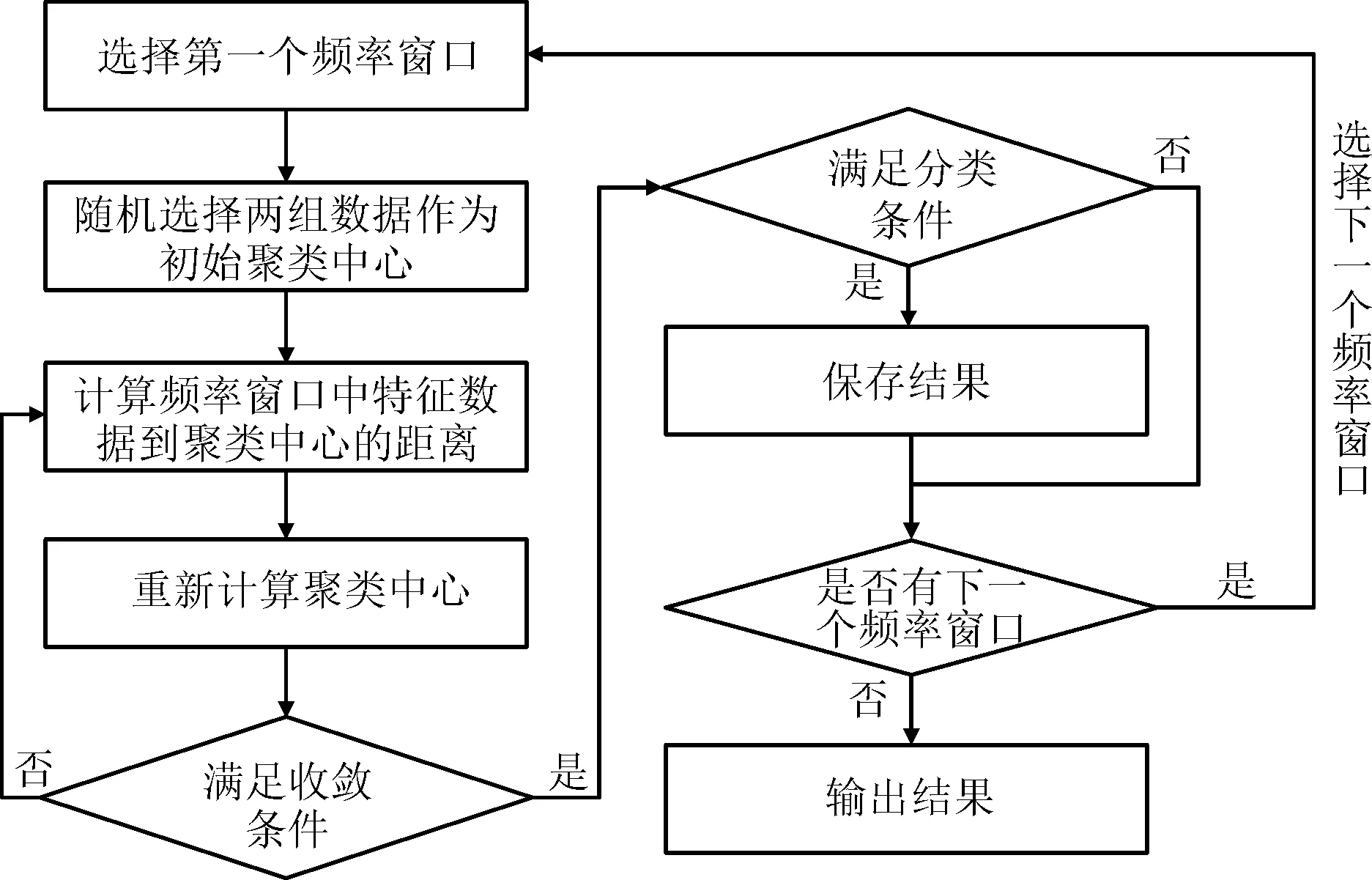
图6 基于频率滑窗的故障模式判别方法流程图Fig.6 Flow chart of fault mode discrimination method based on frequency sliding window

这个算法的流程类似于两层循环嵌套,内循环穷举聚类中心,外循环穷举频率窗口。针对每一类故障,找到所有能够区分该系列试车的健康状态的聚类中心以及其对应频率窗口,保存成为检测该类故障模式的模型。若新输入一组发次的试车数据,其正常与故障工况可用某类故障模式识别模型区分,则可判定新输入试车数据的故障类别含有该类故障。

4.2 算法步骤

滑动频率窗口特征提取的运行步骤如下:①选择第一个频率窗口;②从试车数据中随机选择两个作为初始聚类中心;③计算该频率窗口中的特征数据到各个聚类中心的距离;④重新计算聚类中心;⑤计算测量函数至收敛,或计算到最大迭代次数,得到分类结果;⑥移动到下一个频率窗口重复以上步骤。

4.3 测试结果

本次试车数据共有R0.2、R1.2、R3、R5裂纹这4种故障类型,考虑到故障样本数量以及车次包含的参数等因素,对R0.2、R5进行训练。在测试时根据训练时得到的重点频段进行故障特征聚类,不同的故障类型对应不同的频段。经过训练的故障模式判别模型的测试结果如表6所示,可知跨车次训练得到的分类模型可以验证某一试车数据是否具有相关故障。

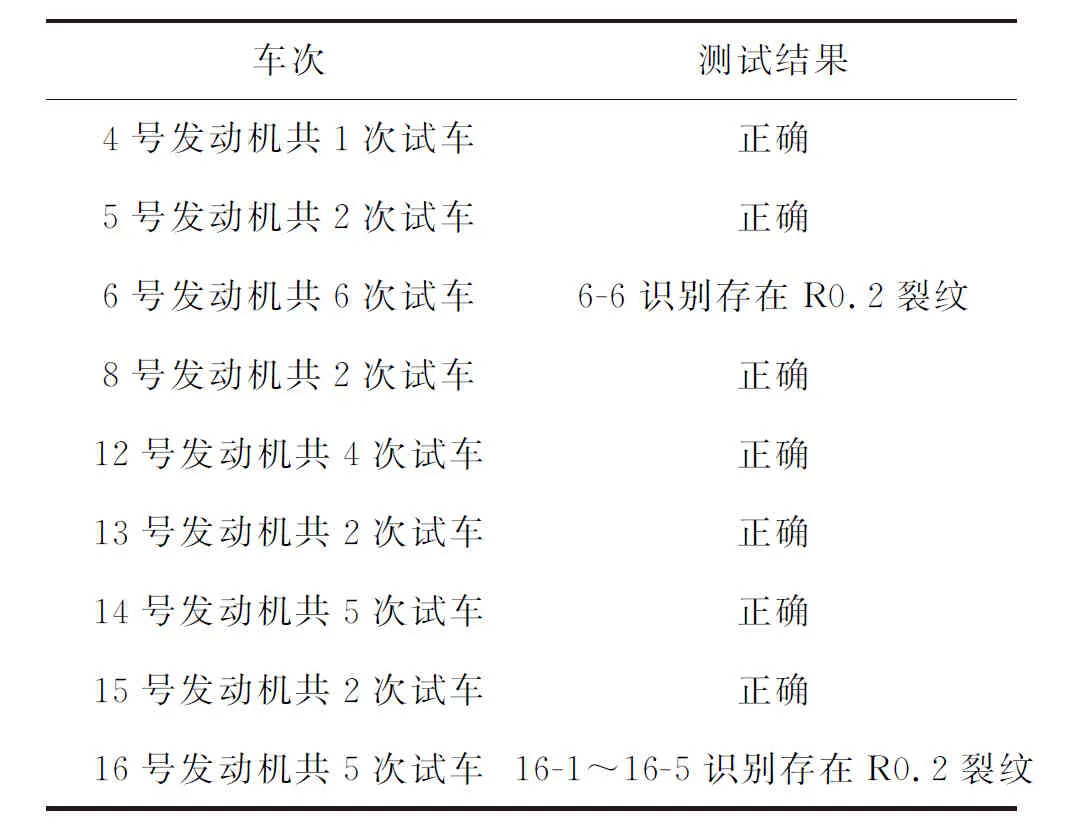
表6 R0.2故障模式识别结果Table 6 R0.2 fault mode detection result table

R0.2故障模式识别模型采用的是试车发次6-1～6-5和16-6联合训练,异常区间为2.187 5～2.5 kHz。从分类结果来看,将存在R0.2故障的6-6与其他发次区分出来,其中16-5发次经过上文算法检验,存在较大的故障可能性。而16-1～16-4虽然没经过拆机分解,但通过本节试验测试暴露其存在安全隐患,值得相关人员开展后续研究。试验一共涉及29次试车,R0.2故障模式识别准确率为86.2%。此次R5故障模式分类试验结果采用8-1和12-1车次联合训练的模型,异常区间为0～0.312 5 kHz。R5故障模式识别结果如表7所示,可知存在R5故障的7-2、7-3均被识别出,同时2-5、2-6存在分类错误,R5故障模式识别准确率为95.5%。

表7 R5故障模式识别结果Table 7 R5 fault mode detection results

综上,本文所提方法在负样本数量较少的情况下表现出良好的准确率。同时,该方法在训练模型的能够给出不同裂纹模式对应的频率异常区间,可为研究人员提供故障相关的线索,用于其他诊断方法。

5 总 结

随着计算机技术、数据存储技术和数据分析技术的快速发展,基于数据驱动的故障诊断技术将会成为未来很长时间内的重要研究与工程应用方向。本文基于某型液体火箭发动机试车历史数据,构建了一种数据驱动的故障检测算法模型,能够处理不同工况下的火箭发动机数据,并在该型发动机历次试车数据集上进行测试,取得了较好的效果。基于故障检测算法的结果,本文构建了一种基于频率滑窗与聚类的故障模式判别方法,可以实现R0.2、R5裂纹模式的识别,并提供不同裂纹模式对应的异常频率区间。

经验证,本文所提算法在发动机试车数据分析过程中可有效检测、识别液体火箭发动机涡轮泵特定故障,能够形成一套标准的分析工具,降低传统发动机试车数据分析方式对于技术人员人力与经验的依赖,并有效提升分析过程自动化程度,实现降本增效。