计及出行行为调整的综合能源系统双层博弈优化策略
2024-04-10贾士铎康小宁田博文崔金旭萧淑文李昕盈
贾士铎,康小宁,田博文,崔金旭,萧淑文,李昕盈
(西安交通大学电气工程学院,710049,西安)
随着“碳达峰、碳中和”目标的提出,推动清洁能源转型,构建高效、低碳、清洁的新型电力系统刻不容缓[1-2]。电热氢综合能源系统(ETH-IES)能够实现多种能源的交互响应和互补互济,显著提高能源利用率[3-5]。此外,氢燃料电池汽车(FCV)和电动汽车(EV)作为灵活性资源参与综合能源系统的调度,有效提高了系统运行经济性和环保性[6-8]。
目前,计及不确定性因素的同时合理规划ETH-IES与新能源汽车的协调运行是面临的重要挑战之一。文献[9]采用蒙特卡洛法模拟电动汽车无序充电,充分考虑源侧风光出力和负荷侧价格型需求响应等过程中的不确定性因素进行经济调度。文献[10]在计及风光不确定性的基础上,提出了综合能源系统与EV双层优化模型,采用拉丁超立方采样处理风光随机性。文献[11]提出了一种考虑碳交易和电动汽车充电负荷的工业园区综合能源系统调度策略。以上文献在考虑了EV负荷和不确定性因素的基础上制定了日前优化调度策略,但未考虑EV实时并网数量的随机性。文献[12]构建了兼顾配电系统安全和用户充电等待成本的双层实时优化调度模型。文献[13]实时优化各EV充电功率以实现经济性最优。以上文献在实时阶段采用单断面的优化,在实际运行时会引入较大误差[14]。模型预测控制(MPC)可以很好地解决含多种不确定因素的优化控制问题[15-16],但在MPC滚动优化过程中,还需要抑制车主按照个人意愿无序改变充电计划的行为。
为了考虑综合能源系统中不同主体的利益竞争行为,较多的学者结合博弈论进行优化[17-19]。文献[20-22]基于主从博弈模型分析售电公司和用户在电力市场中的互动机制。文献[23]提出了一种考虑动态参数的阶梯型碳交易机制和需求响应的园区级综合能源系统主从博弈优化调度方法。文献[24]提出了基于纳什谈判合作博弈理论的多综合能源系统联合规划方法。以上研究均采用单一的博弈方法,实际中系统内的不同主体之间既存在非合作博弈关系还存在着合作博弈关系,并且考虑车辆出行计划临时改变带来的不利影响,通过迭代优化出行计划调整惩罚单价的研究尚处于空白状态。
为此,本文建立了考虑车主出行行为调整的电热氢综合能源系统双层博弈优化运行策略。首先,在MPC第1阶段建立一主多从Stackelberg博弈模型,引入车辆出行计划调整惩罚机制,考虑各主体利益的同时减小了车辆出行计划临时改变所带来的不利影响;其次,基于ULA和NEVLA之间存在的合作博弈关系,在MPC第2阶段建立合作博弈模型并根据Shapley值法分配收益,滚动优化过程中实现各个主体利益最大化,并保证调度的安全性和准确性;最后,将所提策略和算法应用到某电热氢综合能源工业园区以验证其有效性。
1 计及出行行为调整惩罚机制的双层博弈调度框架
所提调度框架集综合能源系统运营商、新能源汽车负荷聚合商以及用户负荷聚合商于一体,协同互联能源网络,能够提供相比电网更加灵活的电价策略,对于鼓励用户科学用能具有积极作用。基于双层博弈的滚动优化调度框架如图1所示,该框架基于两阶段MPC滚动优化,时间窗为24、1 h,时间步长为1 h、5 min,结合实时数据,提高调度的准确性。

图1 基于双层博弈的滚动优化调度框架Fig.1 Rolling optimization scheduling framework based on two-layer game
在第1阶段中,考虑基于系统运营商的报价,新能源汽车负荷聚合商与用户负荷聚合商能够通过优化各时段的需求功率获得更高的利益。该阶段包含了定价决策层和定量决策层,两层存在先后次序,彼此互相影响,符合主从博弈的逻辑结构,因此构建以IESO为领导者,ULA、NEVLA为跟随者的主从博弈模型。在此基础上,引入惩罚博弈机制,即上层的系统运营商通过制定车辆出行计划调整惩罚成本,抑制车主按照个人意愿无序改变充电计划的行为,避免新能源汽车负荷聚合商频繁调整EV集群充放电计划,减小实时调度功率偏差。
在第2阶段中,根据最新的负荷功率预测值和新能源汽车接入情况,ULA、NEVLA可以调节自身的灵活性负荷来平抑预测功率误差和车主出行行为调整带来的偏差功率,当其自身灵活性资源不足以消除该偏差功率时,可以与另一个主体进行能量交换,避免向IESO支付高昂的申报偏差惩罚费用。因此,两者可以通过相互协调、结盟减小自身的成本,并且通过合理的分配策略能够使联盟形式下的成本显著低于自身单独运作的成本,构建ULA和NEVLA的合作博弈模型。所提框架将双层博弈模型嵌入到MPC滚动优化模型中,以期在实时优化过程中实现各个主体利益最大化,并保证调度的安全性和准确性。
2 电热氢综合能源系统实时调度模型
本文所研究的电热氢综合能源系统的结构、各设备模型及参数可参考文献[25-26]。
2.1 MPC滚动优化第1阶段
综合能源系统运营商的能源交易包括定价决策、定量决策两个子阶段。这两个阶段按照先后顺序进行,彼此相互影响,通过迭代最终达到均衡状态。定价决策是上层IESO作为领导者,制定出售电价、热价、氢价及车辆出行计划调整惩罚价格,定量决策是下层ULA、NEVLA作为跟随者,分别根据价格信号调整灵活性资源,因此下层的最优决策是基于上层决策变量的结果。
2.1.1 综合能源系统运营商模型
运营商在考虑供能侧出力计划和用能侧负荷、新能源车辆负荷及车主临时改变出行计划情况的基础上制定价格策略,从而实现自身效益最大化,可表示为
maxBIESO=IIESO-Futility-Fom-Fmt-Fe
(1)
(2)
(3)
(4)
max{0,St-St-1}Cmts+
(5)

(6)

为防止问题退化,避免用能侧直接与电网交易,需要满足如下约束[24]
(7)
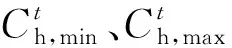
此外,售电、售热、售氢价格还需满足[24]
(8)
(9)
(10)
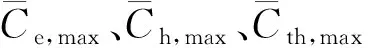
2.1.2 用户负荷聚合商模型
ULA基于上层制定的价格信息优化自身的可平移和可削减电热氢负荷的功率,以期获得最大的消费者剩余,具体表示为
(11)
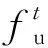
(12)
式中:ve、αe分别为电能消费的一次项、二次项偏好系数;vth、αth分别为热能消费的一次项、二次项偏好系数;vh、αh分别为氢能消费的一次项、二次项偏好系数。
用户负荷由固定、可平移和可削减负荷功率3部分组成,具体表示为
(13)
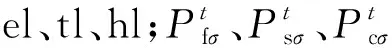
式(13)需要满足如下约束条件
(14)
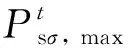
2.1.3 新能源汽车负荷聚合商模型
NEVLA旨在考虑充能成本及EV蓄电池退化成本的基础上,最大化车主的充能满意价值,可表示为
(15)
(16)
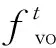
根据放电深度的定义和放电深度与可循环次数的关系,可以得到蓄电池的退化成本[26]
CBde(t,αDOD(Δt))=
(17)
(18)
式中:CBde为单次循环的退化成本;PB为蓄电池功率;Cre表示蓄电池的替换成本;LB为蓄电池寿命拟合曲线;EBA为蓄电池实际满容量;ηBc、ηBd分别表示蓄电池的充电和放电效率系数;αDOD为放电深度;Ea为累计交换能量;g(t)为功率流方向标志。
2.1.4 主从博弈模型
根据以上分析,ULA和NEVLA基于IESO的价格信息调整自身灵活性资源,而他们的运行方式又会对IESO制定价格产生影响,此过程符合主从递阶结构的动态博弈,因此建立了以IESO为领导者,ULA和NEVLA为跟随者的一主多从Stackelberg博弈模型,可以表示为
G={N;ρIESO;{δNEVLA,δULA};FIESO;
{FNEVLA,FULA}}
(19)
上述博弈模型中分别包含参与者、策略和收益,具体表示如下:领导者与跟随者均为参与者,可以表示为N={IESO, NEVLA, ULA};IESO的策略为售出的电价、热价和氢价以及车辆改变计划惩罚价格,可以表示为ΚIESO=(Ce,s,Ch,s,Cth,s,Cpenalty);NEVLA的策略为各时刻的EV集群充放电功率和FCV集群加氢功率,表示为δNEVLA=(PV2G,PFCV);ULA的策略为各时刻可平移和可削减负荷功率,表示为δULA=(Psσ,Pcσ);各参与者的收益为各主体的目标函数,分别通过式(1)、(11)、(15)计算。
2.2 MPC滚动优化第2阶段
2.2.1 ULA和NEVLA合作博弈模型
在第2阶段中,由于预测功率误差和车主出行行为调整影响,ULA、NEVLA的实际功率值与第1阶段申报值存在偏差,因此可以通过自身的灵活性资源以及与另一主体进行能量交换来消除该功率偏差。若仍无法消除,则向IESO支付申报偏差惩罚费用。因此,该模型的目标函数为
(20)
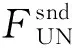
式(20)需满足如下约束条件
(21)
(22)

2.2.2 综合能源系统运营商模型

(23)

2.2.3 基于Shapley的联盟收益分配
Shapley值法属于求解合作博弈模型的数学方法,其特点在于根据联盟内各主体的边际贡献进行分摊,对于参与联盟ULA和NEVLA两个主体,其运行成本计算公式为
(24)
(25)
式中:K为子集c中包含主体的个数;ci为合作联盟中包含第i个主体的所有子集;δ为加权因子;v(c)为子集c产生的运行成本;v(c/i)为子集c中除去第i个主体后的总运行成本。
3 求解方法
MPC滚动优化第1阶段中的领导者IESO优化模型为大规模非线性规划问题,跟随者ULA和NEVLA的目标函数为二次函数,并且在竞争型电力市场中信息互不透明。为此,本文采用一种沙丘猫群体优化算法与二次规划(SCSO-QP)联合的分布式求解算法。MPC滚动优化第2阶段中ULA和NEVLA的优化模型均为线性规模,采用CPLEX求解器进行求解。SCSO算法由于篇幅限制,具体内容见文献[27]。模型求解可归纳为算法1。
算法1基于双层博弈的滚动优化调度模型求解方法,步骤如下:
1. 运行MPC滚动优化第1阶段,初始化tu=1
2. fortu=1 toTu,do
3. 读取电热氢负荷及风电光伏出力短期预测值
4. 采用SCSO-QP分布式协同算法求解MPC滚动优化第1阶段的主从博弈模型
5. 将决策变量作为MPC滚动优化第2阶段TlΔtl+Δtu时间窗内的参考值
6. fortl=1 toTl,do
7. 读取电热负荷及风电光伏出力超短期预测值
8. 采用CPLEX求解MPC滚动优化第2阶段的合作博弈模型
9. end for
10. 反馈蓄电池、超级电容以及储热储氢装置的状态变量给MPC滚动优化第1阶段
11.end for
4 算例分析
4.1 算例参数
以某典型综合能源工业园区为算例,对本文所提的基于双层博弈和MPC的ETH-IES协同滚动优化运行策略进行仿真分析。EV及FCV容量参数及随机特性参数参考文献[26]。将EV负荷分为4类:①全天停泊在充电站的EV;②日常工作通勤的EV;③有紧急充电需求的EV;④有临时驶出需求的EV。其中,第④类EV负荷在当前停车场EV总数的占比不超过10%。采用蒙特卡洛模拟法得到 EV的接入时刻、离开时刻、初始荷电状态、期望荷电状态等基本信息[26],对于FCV的蒙特卡洛模拟方法与EV类似。
临时改变出行行为的汽车数量设置方法如下:原计划于8:00出行车辆中10%的车辆提前至6:00出行,另有15%的车辆提前至7:00出行。用户对电能、热能及氢能的偏好系数ve、αe、vth、αth、vh、αh分别为0.000 9、1.5、0.001 1、1.1、0.001、1.2[22],热价上、下限为0.9、0.3元/(kW·h),氢价上、下限为1.0、0.4元/(kW·h),最大平均售电、售热、售氢价格为1.0、0.8、0.9元/(kW·h)。该算例在MATLAB2021b环境下运行,第1阶段耗时279.2 s,第2阶段耗时23.1 s,满足MPC在线运行的需求。
4.2 结果分析
4.2.1 MPC滚动优化调度结果
系统中电能部分的MPC滚动优化结果如图2所示。由图2(a)可知:3:00—8:00期间,电价低谷,可通过主网购电弥补部分功率缺额;11:00—12:00和16:00—17:00期间电价较高,此时蓄电池释放低峰期间储存的电能,微型燃气轮机输出最大功率以最大程度出售电能;20:00—22:00期间,负荷高,电价峰值,优先利用蓄电池和燃料电池来满足需求,剩余负荷缺额再通过购电来弥补。在整个调度周期中,蓄电池在用电低谷时储存电能、在用电高峰时卖出电能,燃料电池、电解槽和储氢罐在电低谷时将电能转化为氢能储存、在电高峰时将氢能转化回电能,大大提高了综合能源系统的运行经济性和灵活性。
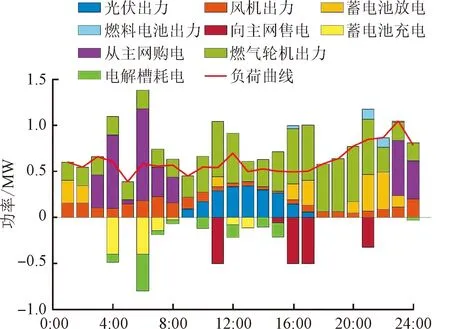
(a)第1阶段滚动优化结果
由图2(b)可知,由于叠加了预测功率误差,在实时调度中实际值与计划值存在偏差,因此需要调整各单元出力来平抑不平衡功率。可以看出,在调度过程中优先使用储能等调节成本较低的单元,若仍不满足要求,则改变微型燃气轮机出力和主网联络线的功率值。
系统中热能部分的MPC滚动优化结果如图3所示。由图3(a)可知,由于地源热泵属于电热耦合设备,而电解槽和燃料电池均为电热氢耦合设备,因此其出力受电价影响较大。在4:00—8:00期间系统多发多储,以期在电价峰阶段减小对电热耦合及电热氢耦合设备的依赖;在10:00—13:00和19:00—21:00期间,电价处于峰阶段,优先使用储热装置中存储的能量。由图3(b)可知,第2阶段中热网部分的各单元出力与第1阶段调度计划值差异较小,所产生的不平衡功率优先由储热装置等调节成本较低的设备平抑。

(a)第1阶段滚动优化结果
氢负荷供给情况如图4所示,5:00—6:00期间分时电价低谷,廉价的电能转化为氢能进行储存。在19:00—20:00期间由于热负荷较高,储热装置余量不足,考虑经济性及运行约束,增加了电解槽出力,由于电热氢耦合效应,过剩的氢能储存在储氢罐中。

图4 氢部分MPC滚动优化结果Fig.4 Hydrogen optimization results of MPC rolling optimization
IESO的定价策略如图5所示,图5(a)中IESO在当地电网提供的分时电价和上网电价的包络线内制定售电价格策略,与电网相比为用能侧提供了更优的价格,在8:00—9:00和12:00—13:00期间IESO提供了相比于电网低得多的价格,旨在促进新能源消纳,避免弃风弃光的现象。图5(b)、5(c)分别表示IESO制定的售热售氢价格策略,通过价格引导ULA、NEVLA的负荷需求响应,在满足功率平衡约束的同时提高IESO的自身收益。

(a)出售电价优化结果
图6给出了IESO车辆出行计划调整惩罚价格的优化结果。由图6可知,在6:00—8:00期间,车主改变出行计划的意愿较为强烈,有较大的可能提前驶离以适应不同的天气情况及道路拥堵情况,因此IESO在此期间制定较高的惩罚价格以抑制车主不遵循初始制定的充电计划行为。
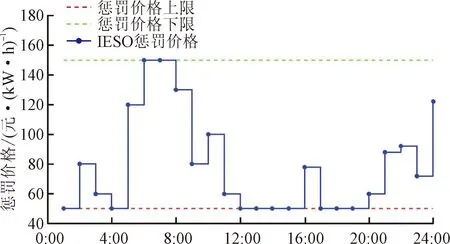
图6 IESO车辆出行计划调整惩罚价格优化结果Fig.6 IESO vehicle travel plan adjustment penalty price optimization results
本文将双层博弈机制嵌入了MPC滚动优化模型,可计算出当前时间窗内的最优策略后滚动时间窗,然后继续进行优化计算,就可以得到每个时间节点对应时间窗的最优迭代曲线,最终将各个时间窗对应的结果组合成最优迭代收敛平面,如图7所示。由图7(a)可知,随着迭代次数的增加,每个时间窗内的IESO收益均有所增加,不同时间节点的时间窗对应的IESO收益也有较大差异,在2:00—7:00及15:00对应的时间窗有着较大的收益值,而1:00、8:00、11:00和21:00的时间窗对应的IESO收益值达到低谷。由图7(b)可知,随着迭代次数的增加,每个时间窗对应的ULA剩余价值逐渐减小,可见领导者和跟随者的收敛趋势不同,体现了博弈过程。当达到Stackelberg均衡后,各主体策略不再改变,说明在该策略下,任何参与者都不能通过独立改变策略而获得更多收益。

(a)IESO收益迭代平面
对比本文所提双层博弈模型与仅在MPC第1阶段引入主从博弈模型的结果,ULA调节成本分别为 642.27、698.62元,NEVLA充能成本分别为 1 232.65、1 372.01元,因此双层博弈模型的成本分别降低了8.07%、10.16%,从而验证了本文所提策略的有效性。
4.2.2 对比分析
对比所考虑的4种策略,策略1为本文所提策略,同时考虑惩罚博弈机制和MPC滚动优化策略;策略2仅考虑MPC不考虑惩罚博弈机制;策略3仅考虑惩罚博弈机制而采用单断面的优化策略;策略4不考虑惩罚博弈机制且采用单断面的优化策略。不同策略下的指标对比如表1所示,策略1下的IESO总收益相比于其他策略分别提升了4.43%、7.75%、14.00%,ULA剩余价值分别增加了6.48%、12.18%、13.75%。EV负荷调度成本相较于策略2、3的结果分别减少了13.64%、4.43%,说明引入MPC和惩罚博弈机制对实际情况下的EV充放电计划有所改进,并且减小了功率调度偏差,提高了系统运行经济性。
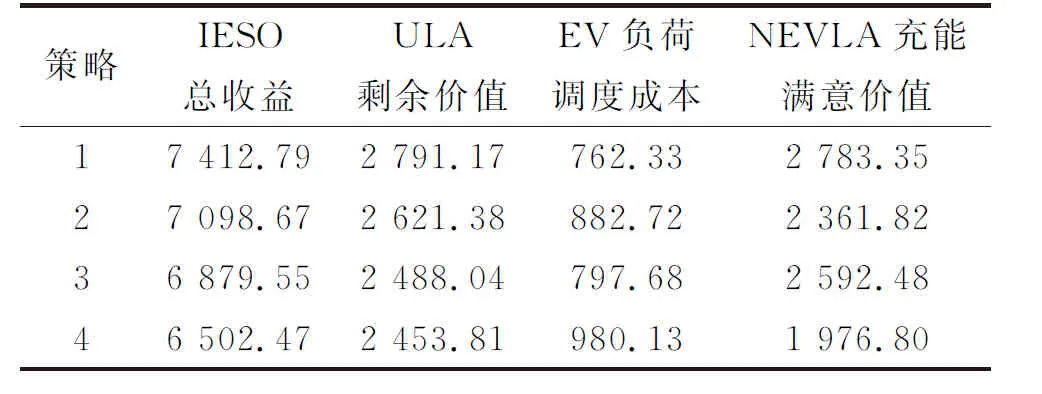
表1 不同策略下的指标对比Table 1 Index comparison under different strategies 单位:元
为了进一步验证MPC策略及惩罚博弈机制对于主网联络线跟踪的作用,将所提策略的主网联络线跟踪偏差惩罚成本与其他策略的结果进行对比,如图8所示。由图8可知:引入惩罚机制后,原本在6:00—8:00期间改变出行计划的车主大部分继续按照原计划实行,从而减小了负荷调度偏差,降低了主网联络线跟踪偏差惩罚成本;而引入MPC滚动优化策略后,进一步消除时间窗内的调度偏差,减小了跟踪偏差惩罚成本。
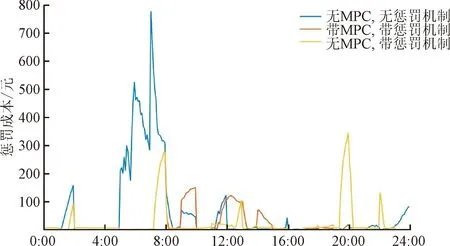
图8 主网联络线功率跟踪偏差惩罚成本Fig.8 Tie-line power tracking deviation penalty cost
5 结 论
本文针对含电动汽车和氢燃料电池汽车的电热氢综合能源系统提出了一种考虑车主出行行为调整的双层博弈优化运行策略,将所提策略与算法应用到某电热氢综合能源工业园区,得到如下主要结论。
(1)将所构建的Stackelberg-Shapley双层博弈模型嵌入MPC滚动优化模型中,在提高调度准确性的同时,对系统内各主体利益协调分配产生积极作用。
(2)在MPC第1阶段的Stackelberg博弈模型中引入车辆出行计划调整惩罚机制,抑制车主按照个人意愿无序改变充电计划的行为,减小实时调度功率偏差。
(3)应用SCSO-QP的分布式求解算法,在得到各主体均衡解的同时可以保护各参与者隐私。
