基于电网GNSS站的区域对流层延迟改正建模研究
2024-04-09江俊飞王磊叶世榕罗颖婷李大江鄂盛龙赖诗钰
江俊飞,王磊,叶世榕,罗颖婷,李大江,鄂盛龙,赖诗钰
(1.广东电网有限责任公司电力科学研究院,广东 广州 510080;2.国家卫星定位系统工程技术研究中心,湖北 武汉 430000;3.中山大学 测绘科学与技术学院,广东 珠海 519080)
目前,无人机自动巡检技术已成为电网公司开展设备巡视和运维的主要手段之一[1],其依赖于全球卫星导航系统(global navigation satellite system,GNSS)和地面服务系统。为了能保障无人机定位的稳定性和可靠性,广东电网有限责任公司自建了连续运行参考站(continuous operating reference station,CORS)定位服务系统;但在实际应用中受广东地区地理位置影响,无人机高精度定位仍存在一定的定位误差。其中,对流层天顶总延迟(zenith total delay,ZTD)是定位大气误差中的主要误差,影响定位精度可达至分米级别。ZTD产生的原因是卫星信号在穿越对流层过程中受水汽等大气介质影响,传播路径和传播速度发生改变。通常情况下,ZTD分为静水延迟和湿延迟,湿延迟作为受大气水汽影响较大的部分,是ZTD精准估算的难点。采用常规的Hopfiled模型[2]与Saastamonien模型[3]获取ZTD,在水汽影响较大区域其精度较差,并且依赖于气象站实测气象数据,成本较高。为避免采用实测气象数据,有学者通过插值表或球谐函数构建气象参数模型,如Boehm等人的GPT系列的模型[4-6]、Collins等人的UNB3[7]和UNB3m[8]模型、Penna等人的EGONS模型[9],以及Mateus等人通过对ERA5再分析资料进行时序分析而最新提出的HGPT模型[10]和HGPT2模型[11]。为了更加直接地构建ZTD模型,并且避免通过参数计算ZTD引入的偏差,部分学者直接针对经高精度解算或数值气象资料解算的长期ZTD周期性变化来构建模型,如Krueger等构建的TropGrid模型[12],Schüler等人改进的球谐函数模型TropGrid2[13],Yao等人构建的ITG模型[14]、GZTD模型[15]、GZTD2模型[16],以及黄良珂等人构建的GGZTD模型[17]。上述模型主要基于历史ZTD的时间序列,能反映出对流层延迟的长期变化趋势,误差为4~6 cm;但其很难反映对流层延迟的短期变化,且在不同区域的表现效果并不相同,在一些特定的、湿延迟受水汽影响较大的地区,这些经验模型的精度影响实时精密单点定位的快速解算以及ZTD反演水汽的准确度。同时,近些年厄尔尼诺现象的频繁发生,较大影响了我国的沿海地区,导致水汽剧烈变化[18]。构建区域实时ZTD模型不仅对实时定位有着重要意义,也能为灾害气候预警提供一项可靠的数据源[19]。
为解决广东地区常规ZTD计算模型精度不够高的问题,本研究首先分析ZTD随高程变化常用的拟合函数(指数函数、高斯函数),提出新的分段拟合方式(在0~2 km采用线性拟合,2~8 km和8~50 km分别采用指数函数拟合),并以广东地区2020—2022年的ERA5数据和2023年1—3月的GNSS站点数据实时解算ZTD,构建修正后的区域实时ZTD模型;接着,根据3年ERA5数据,使用该模型计算得到分段拟合函数系数的时间序列,并利用计及年、半年和日周期变化的傅里叶级数拟合该时间序列,获得ZTD经验格网模型;然后,计算用经验模型在GNSS站点位置处求出的ZTD与站点实时GNSS-ZTD的偏差,利用反距离加权的方法计算出经验格网点的实时偏差,并补偿格网点处的经验拟合函数,获得具有实时特性的ZTD格网数据;最后,利用广东电网CORS服务系统历史数据,对获得的格网数据进行精度验证。
1 基于ERA5再分析资料的广东地区ZTD精细建模
ERA5是由欧洲中期天气预报中心(European Centre for Medium-range Weather Forecasts,ECMWF)所研发和维护的全球气象重分析数据集,以高分辨率和丰富的气象参数描述地球大气的时空变化[10]。该数据集的空间分辨率为0.25°×0.25°,时间分辨率为1 h,其包含了自1979年以来的温度、湿度、风速、气压、降水等多种气象参数,不仅涵盖了地球表面的情况,还考虑了不同垂直层次的大气特性。ERA5数据以NetCDF格式提供。本文采用的ERA5数据空间分辨率为0.5°×0.5°,共计37层气压分层数据,时间分辨率为1 h(下载地址:https://cds.climate. copernicus.eu/)。首先根据ERA5产品中气象参数(气压、水汽压、温度)采用方程计算出每层的大气折射率,再从各层级所处的位置对折射率进行积分求和,最后加上ERA5最高层以上的ZTD,便可以得到每个气压层对应的ZTD(量符号记为KZTD):
(1)
(2)
式(1)、(2)中:N为大气折射率;e为为水汽压,单位hpa;T为温度,单位K;p为气压,单位hpa;φ为格网点所在纬度;H为不同气压层的大地高,H1、Hn分别为第1、n层气压层的大地高,单位km。将顶层气压p代入Saastamonien经验模型,计算得到ERA5气象数据顶层以上的ZTD,因50 km以上大气的水汽含量基本为0,经验公式能够精确计算该高度上的ZTD。经过计算后得到的ERA5数据字段包括时间、经纬度、37层气压层的大地高,以及每层的ZTD。
实时站点数据是使用gamp实时计算出的ZTD数据,数据包括时间、经纬度、大地高和ZTD。
GPT3[6]在ECMWF建立的模型基础上增加了梯度模型,改良了映射函数关系,是目前主流的先验对流层延迟模型之一。该模型只需提供用户坐标和年积日即可获得所需要的气象参数,最后利用Saastamoinen模型获得用户处的ZTD。
HGPT2[11]同样也是一种经验模型,主要是对全球温度、气压和相对湿度的时间序列进行建模,通过自身拟合的气象参数和Saastamoinen模型,来获得全球任意时空的ZTD数据。
1.1 ZTD垂直剖面模型高程归化拟合函数的改进
目前,ZTD常用的垂直拟合函数有指数函数
KZTD=aexpbH
(3)
和高斯函数[20-21]
KZTD=aexp[-(bH)2/c2].
(4)
式(3)、(4)中a、b、c均为拟合系数。随机选取不同经纬度上的格网点,分别采用指数函数和高斯函数进行非线性最小二乘拟合,拟合结果如图1所示。
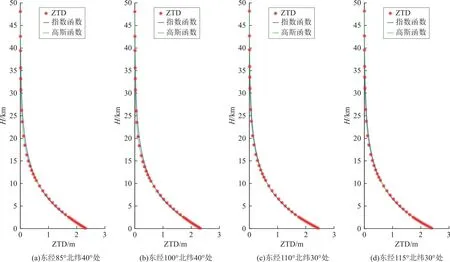
图1 在不同高度的指数函数和高斯函数拟合ZTDFig.1 Exponential and Gaussian functions fit ZTD at different heights
为了进一步观察这2种拟合函数在不同高度处的拟合效果,统计经度73°~133°、纬度3°~53°所有格网点不同高度处的ZTD拟合偏差,其0~50 km区间的偏差曲线如图2所示,将ZTD的拟合偏差记为“DZTD”。
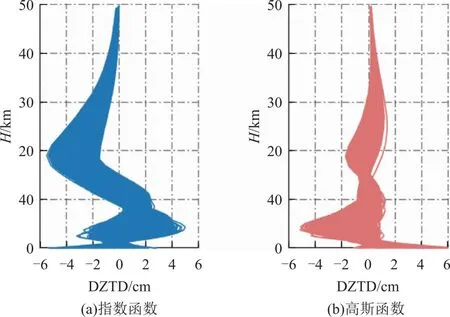
图2 在不同高度的指数函数和高斯函数拟合偏差Fig.2 Fitting bias of exponential and Gaussian functions at different heights
从图2可以看出:指数函数在0~<2 km、2~<8 km、10~<30 km均会出现较大的偏差,最大偏差可达到6 cm;高斯函数在0~6 km会出现较大的偏差,最大也可达到6 cm,但其在高空区域的拟合效果较好,基本都在2 cm以内。无论采用指数函数还是高斯函数,在拟合ZTD与高程的变化关系时,都会在较低高层范围内出现较大的偏差。
通常情况下,GNSS观测站测量高程在3 km以下。经过大量实验,本研究采用如下分段拟合函数(以下简称“分段函数”)来表示不同高度区间内ZTD的变化:
(5)
式(5)中a1—a3以及b1—b3均为拟合形式中的未知参数。从图1可以看出,H在0~<2 km时,ZTD随高程基本是线性变化,故本研究在0~<2 km时使用线性函数;同时由图2可以看出,指数函数拟合的偏差在2~<8 km和20 km左右较大,故在2~<8 km和8 km以上使用指数函数分别进行非线性最小二乘拟合。在经度85°、纬度40°位置,分段函数拟合效果和偏差统计如图3所示。
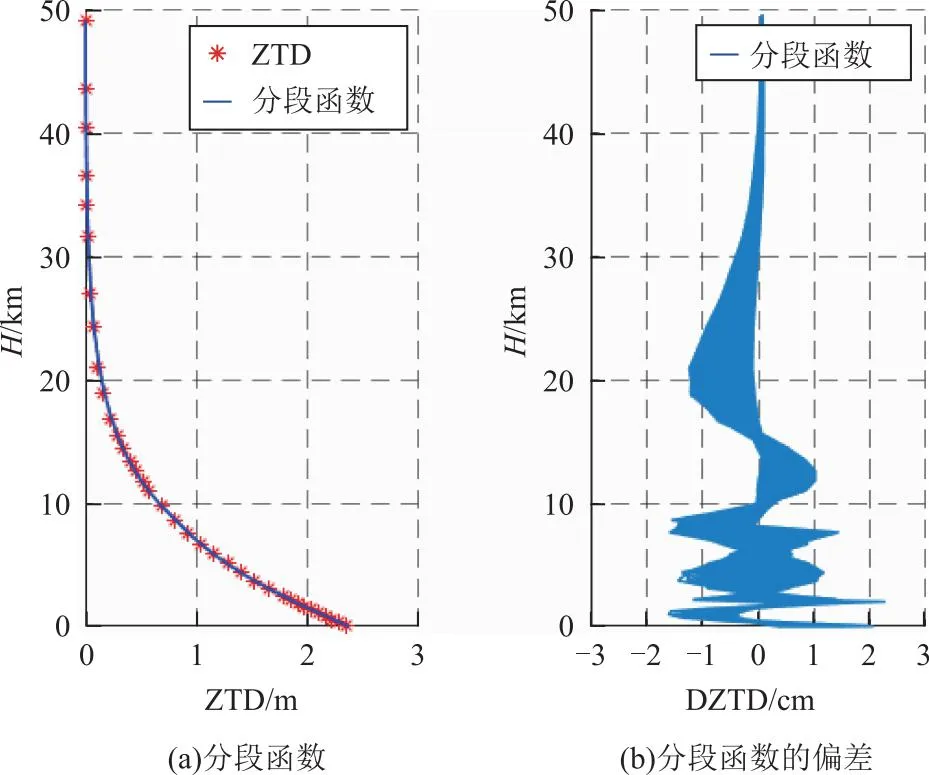
图3 在不同高度的分段函数的拟合ZTD及DZTDFig.3 Segmented function fits ZTD and DZTD at different heights
从图3可以看出,新的分段函数效果较采用指数函数/高斯函数更好,偏差基本在1 cm左右。分段函数的拟合形式避免了高斯函数和指数函数在低空出现较大偏差的情况。统计3种拟合函数在不同高度范围拟合ZTD的均方根误差(root mean square error,RMSE),通过RMSE来表征精度,见表1。
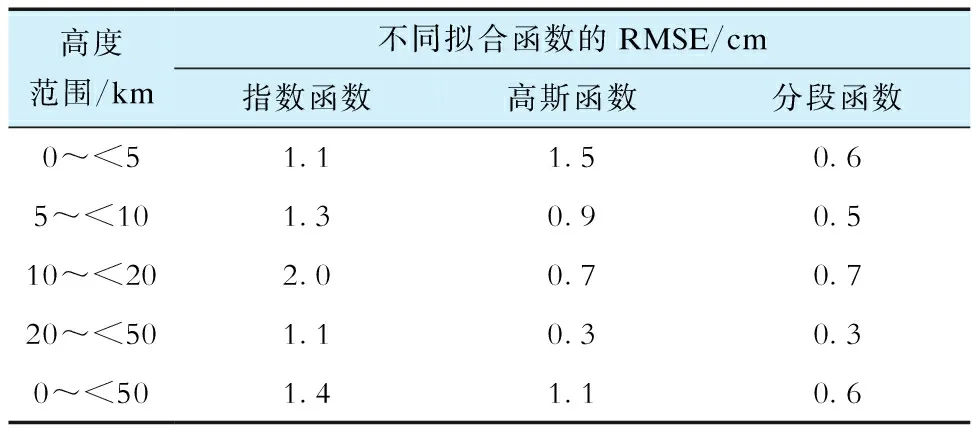
表1 在不同高度范围的指数函数、高斯函数、分段函数的RMSETab.1 RMSE values of exponential,Gaussian,and segmental fitting functions in different height ranges
在0~<5 km的高度范围内,分段函数展现出最低的RMSE,为0.6 cm,相比之下,指数函数、高斯函数的RMSE分别为1.1 cm、1.5 cm;类似地,在5~<10 km、10~<20 km以及20~<50 km的高度范围内,分段函数也呈现出最低的RMSE,分别为0.5 cm、0.7 cm和0.3 cm。总体而言,在任意高度范围内,分段函数都表现出较低的误差。分段函数的0~50 km全高度RMSE(简称为“总RMSE”)为0.6 cm,而高斯函数、指数函数的总RMSE分别为1.1 cm、1.4 cm。
以东经105°和北纬35°为分界线将中国区域划分成东北地区、东南地区、西北地区、西南地区,分别统计这3种拟合函数在不同地区的总RMSE,见表2。
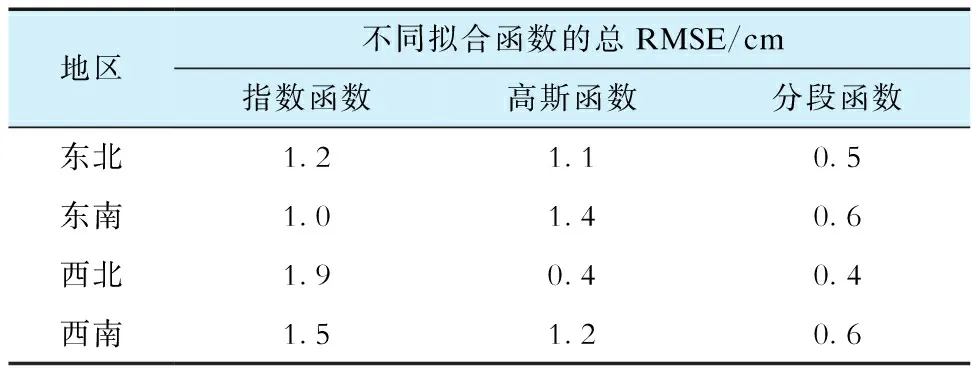
表2 3种拟合函数在不同地区的总RMSETab.2 RMSE values of three fitted functions in different regions
由表2可看出:在东北地区,分段函数表现较好,其总RMSE达到0.5 cm,指数函数、高斯函数的总RMSE分别为1.2 cm、1.1 cm;在东南地区,分段函数的总RMSE为0.6 cm,高斯函数的总RMSE(1.4 cm)略大于指数函数的总RMSE(1.0 cm);西北地区中,高斯函数和分段函数呈现出相同的精度,总RMSE均为0.4 cm,指数函数的总RMSE为1.9 cm,指数函数在西北地区的拟合精度较低;至于西南地区,指数函数、高斯函数显示出接近的精度,总RMSE分别为1.5 cm、1.2 cm,分段函数的总RMSE为0.6 cm。由此可知:分段函数在不同区域的拟合效果都比较稳定,且总RMSE一直保持在0.5 cm左右;指数函数在东北、东南地区的精度比西北、西南地区的精度要较高一些;高斯函数在西北地区精度较高,其余3个地区的精度要稍差一些。
1.2 构建广东地区ZTD格网经验模型
广东地区位于东南沿海地区,根据上述分析结果,采用分段函数来对该地区进行建模,拟合函数见式(5)。使用积分法计算出广东地区ERA5数据2020年1月—2022年1月的、每个格网点不同气压层的ZTD数据,再使用式(5)分段函数计算出每个时刻的拟合函数系数,得到3年拟合函数系数的时间序列。图4所示为格网点(纬度23°、经度113°)拟合系数a1—a3、b1—b3的时间序列,曲线中各数据点对应各年份中整点时刻的数据。
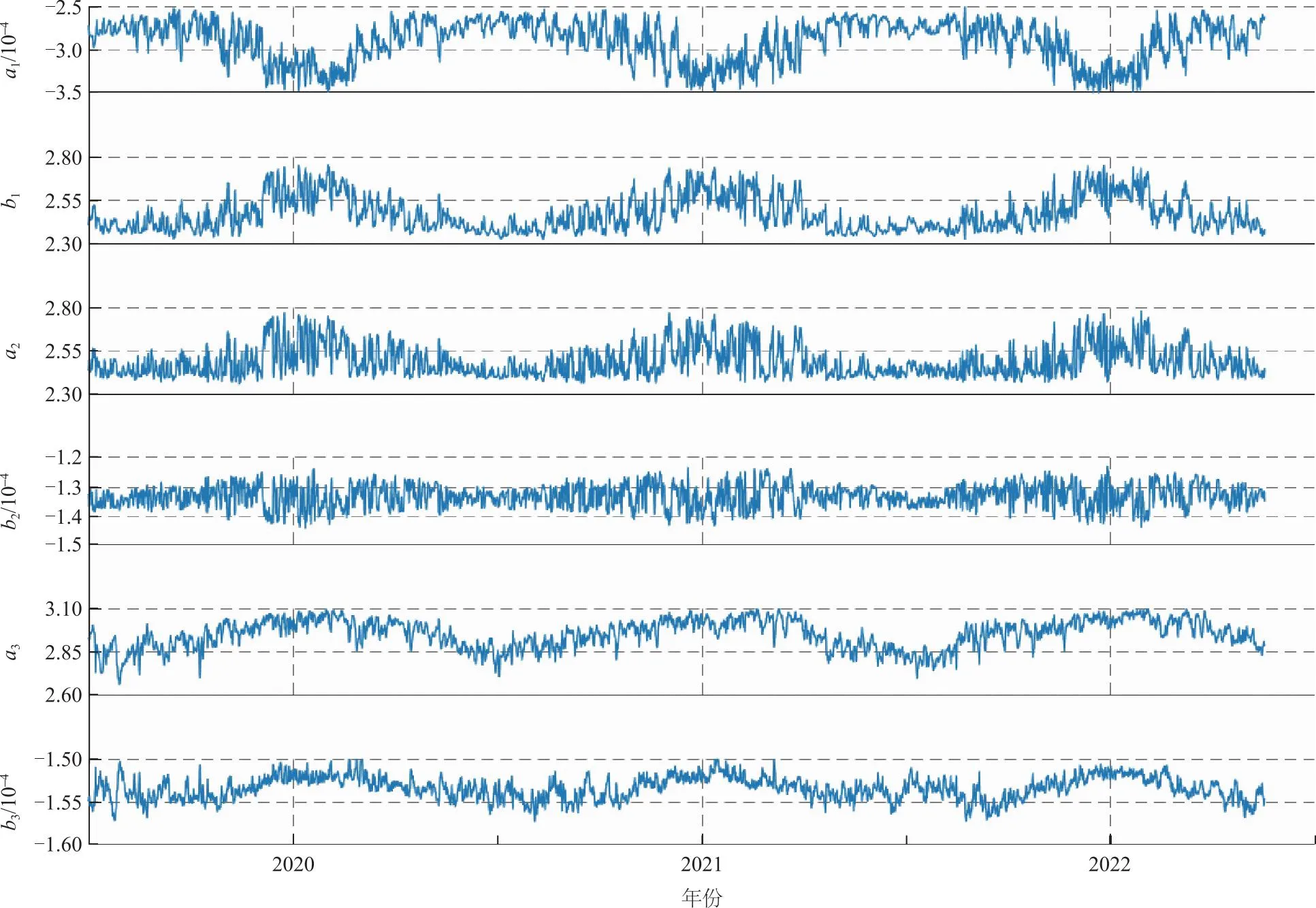
图4 2020年至2022年分段函数系数的时间序列Fig.4 Time series of coefficients of segmented fitting functions from 2020 to 2022
从图4可以看出这些系数具有较强的周期性变化。以系数a1为例,对系数的时间序列进行傅里叶频谱分析(其中采样频率设为1 Hz),结果如图5所示。
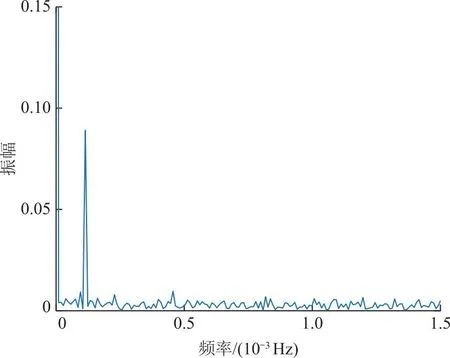
图5 系数a1的频谱分析Fig.5 Spectral analysis of coefficient a1
由图5得到拟合系数的时间序列主要频率,通过傅里叶频谱分析,最终对每个系数采用计及年、半年和日周期变化的傅里叶级数,拟合计算式为
(6)
式中:k、ki(i=1,…,6)均为模型系数,k表示均值项,k1、k2表示年周期项,k3、k4表示半年周期项,k5、k6表示日周期项;tdoy为年积日;thod为日内时;m为分段函数的系数,m∈{a1,a2,a3,b1,b2,b3}。使用式(6)和非线性最小二乘方法,拟合并保存广东地区每个格网点拟合系数的3年时间序列数据,构建完成广东地区ZTD经验模型。输入时间(tdoy和thod)便可以得到任意格网点某个时刻不同高度处的ZTD数据。该模型的空间分辨率为0.5°×0.5°,时间分辨率1 h,区域范围为纬度20°~26°、经度109°~118°。
1.3 实时解算GNSS修正ERA5经验模型
经验模型能反映ZTD的长期变化趋势,但很难反映其短期实时变化,因此可以加入实时站点数据。步骤如下:
a)输入当前时刻的年积日和日内时,获得当前时刻每个格网点的ZTD随高程变化的拟合函数;
b)利用双线性插值得到GNSS站点处的经验ZTD,并与GNSS站的实时ZTD作差,得到经验模型的实时DZTD;
c)搜寻每个格网点距离最近的3个GNSS站点,计算出站点DZTD,然后采用反距离加权的方法获得格网点处的DZTD(将该DZTD记为“DZTDg”);
d)将格网点处的拟合函数加上实时DZTDg,便能得到实时的ZTD格网(将该格网模型记为“Gdgrid”)数据,其格式为时间、经纬度、ZTD随高程的拟合系数,以及计算出来的DZTD。
用户使用步骤:
a)接收到播发的Gdgrid数据后,找到所处格网;
b)输入高程获得4个格网点在用户高程处的ZTD;
c)利用双线性插值计算得到用户所在位置ZTD。
2 模型精度验证
按照实时精密单点定位数据处理方法,计算获得2023年1—3月广东电网96个GNSS站的实时ZTD数据。计算处理策略见表3。

表3 精密单点定位参数设置Tab.3 Parameter setting of PPP
选用广东电网31个GNSS站作为基准站,65个GNSS站作为验证站。选取的基准站和验证站分布均匀,能较好反映不同地区的精度差异。对于参与建模的站,按上述方法对每个格网点进行操作得到Gdgrid数据,并利用验证站对Gdgrid数据精度进行评定,部分GNSS验证站的总RMSE见表4。
从表4可以看出,在这25个验证站上Gdgrid的总RMSE都在1 cm以下,仅有个别站总RMSE在1 cm以上。通过观察验证站位置后发现,导致这些站精度较差的原因是这些验证站多数位于边缘地带,仅有一侧具有基准站,或者是距离基准站较远。GPT3、HGPT2在部分站精度较高,但在有些站会有较大的偏差,原因是GPT3和HGPT2属于经验模型,并没有添加实时数据源,导致在部分地区这2个模型的精度较差。统计在所有验证站Gdgrid的总RMSE分布情况,如图6所示。
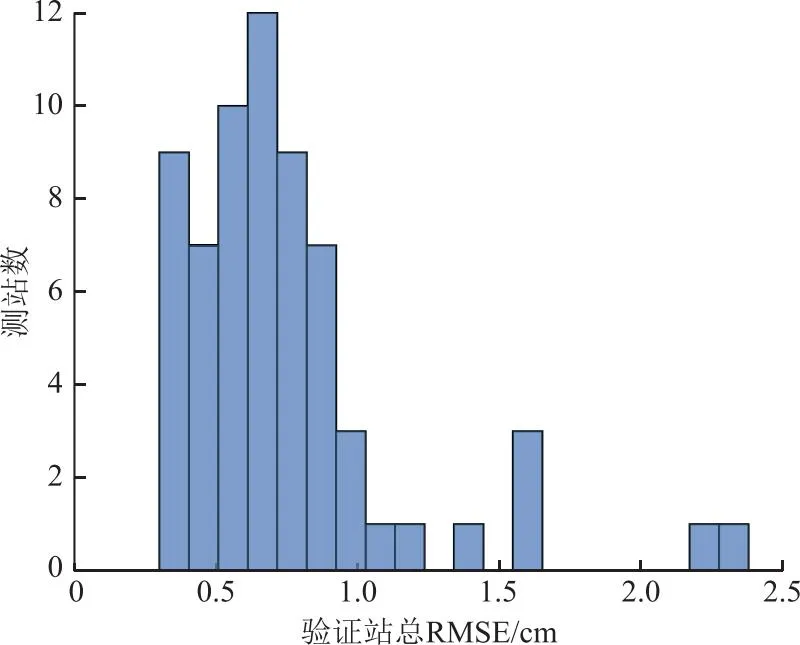
图6 验证站2023年1—3月Gdgrid的总RMSEFig.6 RMSE values of Gdgrid of validation stations from January to March 2023
由图6可以看出,仅有5个站Gdgrid的总RMSE在1.5 cm以上,多数站总RMSE都在1.0 cm以下,可见本文方法获得的实时ZTD数据精度较高。
统计所有验证站在3个月内的总RMSE,并与GPT3、HGPT2经验模型的总RMSE进行比较,见表5。

表5 Gdgrid与GPT3、HGPT2的对比Tab.5 Comparison of GPT3,HGPT2 and Gdgrid
从表5可以看出Gdgrid的总RMSE仅有1.12 cm,远优于GPT3、HGPT2的总RMSE,其中HGPT2精度最差。统计结果表明,相对于经验模型,附加实时数据的修正ERA5的模型精度更高,能够更好反映ZTD的短期变化。
3 结论
本研究针对现有基于指数函数、高斯函数的ZTD模型在低空范围会出现较大偏差的问题,提出基于分段拟合的新建模方法,并采用实际观测数据对模型精度进行了验证,结论如下:
a)本文提出的ZTD模型在海拔高度0~<2 km采用线性函数,2~<8 km和8 km以上分别采用不同拟合系数的指数函数。结果表明分段函数的拟合精度最高,尤其是在0~10 km高度范围,指数函数和高斯函数的RMSE基本在1 cm以上,而分段函数的RMSE在0.5 cm左右,极大提高了ZTD在低空区域的拟合精度。
b)实验结果表明:分段函数在中国不同区域处的拟合精度基本不变,总RMSE维持在0.5 cm左右;指数函数在西北地区精度最差,总RMSE为1.9 cm,在东北、东南、西南地区的总RMSE在1.0~1.5 cm之间;高斯函数在西北地区表现较好,总RMSE仅有0.4 cm,在东北、东南、西南地区精度与指数函数相差不大。
c)根据广东电网96个GNSS站2023年1—3月的实时ZTD数据,对Gdgrid模型格网数据进行精度验证,结果表明仅有5个站总RMSE大于1.5 cm,其余站的总RMSE基本在1.0 cm以下。
d)对比Gdgrid与GPT3、HGPT2模型精度,Gdgrid的精度远优于GPT3、HGPT2,Gdgrid的总RMSE为1.12 cm,而GPT3、HGPT2的总RMSE分别为4.24 cm和5.13 cm。
