分形及规则布置方柱绕流场及气动噪声特性数值研究

2024-04-07陈武韩斐周毅

机械科学与技术 2024年3期

陈武 , ，韩斐 , ，周毅 ,

（1.中国空气动力研究与发展中心气动噪声控制重点实验室，四川绵阳 621000；2.南京理工大学能源与动力工程学院，南京 210094）

流体流经单个或多个障碍物的现象在航空航天领域中处处可见（如飞机起落架及舱体[1]、直升机旋翼[2]等）。柱体绕流是典型的绕流问题之一，由于存在尾流间的相互作用及不同尾流与柱体间的相互作用，相比较单个柱体产生的尾流场，多柱体后形成的尾流场的演化特性更加复杂，研究内涵会更加丰富[3]。

气动噪声是在湍流运动中，伴随流体的压力脉动，通过流体的弹性和惯性作用向远离流动区域空间传播而形成的流动噪声[4]。目前多柱体绕流流场特性和气动噪声特性[5]的研究在航空航天领域中具有重大的研究意义。国内外学者对多柱体绕流及其气动噪声问题进行了一系列的研究[6-16]。Ishigai 等[6]对3 种不同排列的多圆柱组合进行了实验研究，结果表明涡形成区域和康达效应（Coanda effect）对流场特性具有重要影响。Auger 等[7]通过实验研究发现，当相邻圆柱之间的间距不同时，流体流经并列圆柱后产生的旋涡脱落有明显的变化。Zheng 等[8]对3 个并排方柱后的流动进行了数值仿真研究，确定了流场中存在5 种不同的流态，并详细研究了每种流态对应的湍流特性。刘欢[9]采用有限体积方法对低雷诺数下等边布置三方柱绕流进行了数值研究，预测了临界间距比随雷诺数的增加而增大。Xu 等[10]对3 ～ 4 个并排的柔性圆柱体进行了实验研究，探讨了流致振动问题。Inoue 等[11-12]采用二维非定常可压缩Navier-Stokes 方程组的直接求解方法，研究了在低马赫数下的均匀来流场中并列双方柱和并列三方柱所产生的气动噪声特性。杜炳鑫等[13]提出了一种基于流声分解法的绕流噪声预测方法，对低雷诺数（Re=200）下的串列和并列双圆柱绕流噪声问题进行了研究。高威等[14]采用改进型延迟分离涡（Improved delayed detached eddy simulation, IDDES）模型对串列双圆柱绕流进行数值仿真，分析了不同来流速度、圆柱间距比和圆柱直径下串列双圆柱绕流的气动噪声特性。余雷等[15]采用基于非线性k-ε模型的限制数值尺度（Limited numerical scales, LNS）方法对串列双圆柱绕流算例进行了研究。Zhou 等[16]采用直接数值模拟方法对高间距比的双方柱绕流进行研究，并将近场区域非 Kolmogorov 理论的-5/3能谱幂律函数与极端减速事件相联系。

上述的研究大多集中在相同尺度柱体后的尾流及其气动噪声问题。近年来，具有多尺度/分形轮廓的物体（分形格栅[17-21]、不规则端板[22-23]和多尺度边缘的叶轮[24-25]等）产生的尾流引起学者广泛的研究。部分学者认为，分形的多尺度边界在某种程度上可以调控湍流特性[26]。

在航空航天工业领域，分形流动具有相当广阔的应用前景和潜力[27-29]。航空航天面临的主要环境问题之一是机体噪声，而扰流板是产生机体噪声的主要部件之一。Nedić等[27]研究发现机翼装载大孔隙的分形扰流板，能够在保持与常规扰流板类似空气动力学性能的同时将其诱导的气动噪声声压级降低4 dB。Nedić等[28]对NACA0012 机翼常规后缘和非平坦锯齿/分形后缘产生的涡脱落特性及其气动性能进行了实验对比研究。实验结果表明多尺度/分形机翼后缘能够有效改善空气动力学性能。Gehlert 等[29]研究了分形端板对NACA0012 半展翼翼尖涡的影响。结果发现，分形端板的引入对涡的几何结构和湍流特性都有很大的影响。Laizet 等[26]证明了多尺度/分形湍流场中存在所谓的空间尺度展开（Space-scale unfolding, SSU）机制，能够显著提高标量混合效率。Laizet 等[19]首次对二维多尺度方柱阵流场进行了数值研究，揭示了分形排列的影响机制。Baj 等[30]用粒子图像测速技术和三重分解技术，对多尺度方柱阵的湍流近场进行了实验研究。Tao 等[31]采用直接数值模拟的方法研究了两种具有相同阻塞率的方柱布置（分形布置和规则布置），并使用快照本征正交分解方法定量的评估了两种湍流中相干结构特征的差异。

综上所述，前人的研究集中在对分形结构产生的旋涡脱落特性上，对于分形结构产生的尾流气动噪声特性的研究稍显不足。本文采用大涡模拟结合K-FWH 声比拟方法对分形布置方柱尾流场和声场进行数值模拟研究。此外，对相同阻塞率的规则布置方柱尾流场进行了对比仿真模拟，以比较其与分形布置方柱尾流场特性的异同。

1 数值方法及计算几何模型

1.1 数值方法

本文利用壁面自适应局部涡粘（Wall adapting local eddy viscosity, WALE）亚格子模型开展大涡模拟，该模型表达式[32]为

式中Ls=min（kd,CωΔ1/3），k为冯卡门常数，d为距离壁面最近的网格尺度，Cω为WALE 常数。

WALE 模型是在湍流结构的运动和动力学性质的基础上，将转动张量包含在模型中构造而成。该模型的优点是能够正确的反映出近壁区域涡粘系数与垂直壁面距离的三次方成正比的特性，且模型中不含任何有关边界几何尺寸的参数，在复杂的湍流模拟中得到广泛的应用。

本研究对于声场的求解采用K-FWH 声压时域解公式[33]，并根据实际情况简化公式得到瞬时声压p'的时域解，其公式为

本文所采用的K-FWH 方程声压时域解公式由FWH 方程声压时域解结合Kirchhoff 方法得到，该公式不需要求解物体表面压力的法向导数，简化了声压的计算。

1.2 分形及规则布置

本文采用两种不同排列方式的并列多方柱布置（规则布置方柱和分形布置方柱），研究在多方柱后形成的尾流特性及其气动噪声特性。在规则布置中，4 个相同的方柱体并排布置，与来流方向垂直（从下至上依次为Bar1、Bar2、Bar3和Bar4）。在分形布置方柱中，3 种分形尺度的方柱体并排布置，与来流方向垂直（从下至上依次为Bar1、Bar2、Bar3、···、Bar7）。

图1 为两种布置方柱在笛卡尔坐标系上的示意图，其中左边为前视图，右边为侧视图，虚线表示计算域边界，具体的几何细节和计算参数见表1。笛卡尔坐标系的原点设置在Y-Z平面的中心，所有柱体均垂直于X-Y平面。在两种布置中，并排的方柱体放置在XBar/TBar=8 处，XBar表示计算域入口到柱体中心的流向距离，TBar表示柱体流向厚度。基于方柱流向厚度TBar和入口来流速度为3.75 m/s。长度LX、LY、LZ分别表示沿流向、法向和展向的计算域长度，两种布置的计算域大小相同。对于规则和分形布置，两个相邻柱体表面之间的垂直间距Lg/TBar分别为2.33 和1.33。在规则布置中，每个方柱法向厚度为TBar。在分形布置中，采用三次分形迭代的方柱，大尺寸、中尺寸和小尺寸柱体的法向厚度迭代比为T0∶T1∶T2= 4∶2∶1（见图1b））。

表1 规则与分形模型具体几何参数Tab.1 Computational and geometrical parameters of regular and multiscale models

图1 两种布置方柱的示意图Fig.1 Two kinds of square column layout diagram

两种布置具有相同的阻塞率（即σ= 0.30），阻塞率表达式为

式中：Af为方柱横截面面积之和；At为计算域横截面面积（即LY×LZ）。例如，规则布置方柱的阻塞率σ= 4TBar/LY。

在划分网格时采用指数函数对柱体壁面附近网格进行加密，使壁面网格第一层网格Y+≈1。远离壁面的部分采用均匀加密，最后得到规则布置的网格数为6.00 × 106，分形布置为6.96 × 106。展向设置为周期性边界，方柱表面为无滑移壁面边界，其余边界为远场边界。空间离散为二阶迎风格式，时间离散为二阶隐式格式。时间步长设置为Δt=5 × 10-6s，在流场充分发展之后，对流场结果和噪声结果进行统计，取样统计时间为7 × 104个时间步长（对应总时间为0.35 s）。

2 数值方法验证

在研究规则和分形布置方柱引起的湍流特性和气动噪声特性之前，需要验证本文所使用的数值模拟方法的准确性。因此，本文对单方柱绕流进行数值模拟计算用以验证流场计算方法的可行性。与此同时，由于单方柱绕流气动噪声的实验结果较少，国内外学者对于串列双圆柱绕流气动噪声的研究较多，本文采用串列双圆柱模型验证噪声计算方法的正确性。

2.1 流场仿真方法验证

本文研究对象为规则与分形布置多柱体绕流，由于多柱体绕流缺乏相对应的实验或仿真数据，无法直接将数值结果与前人结果进行直接比较。单方柱是多方柱构成的基本元素，多方柱尾流场是多个单方柱尾流相互作用形成的。因此，本小节通过单方柱流场特性与前人结果进行对比，进而验证所采用流场仿真方法的正确性。

本文研究单方柱的边长为L，入口来流速度为Uin，基于方柱边长和来流速度的雷诺数为Rein=UinL/v= 104。

选取方柱柱体中心作为坐标系原点，计算域为：-10L≤LX≤20L，-9L≤LY≤9L，0≤LZ≤4L。对方柱周围进行加密处理，壁面第一层网格Y+≈2，X-Y平面上的计算域网格如图2 所示，总网格数为2.36 ×106，单方柱网格加密方式与分形及规则布置方柱的网格加密方式相同。单方柱绕流的边界条件设置与规则及分形布置方柱绕流相同。时间步长为Δt=5 ×10-6s，取样统计时间为70 000 个时间步长（总时间为0.35 s）。

图2 X-Y 平面上的单方柱计算网格Fig.2 Computational grids in the X-Y plane for a single square cylinder

图3 为无量纲平均流向速度u1/Uin在中心线上的流向演化，文献[31,35]为数值结果，文献[36-39]为实验结果。从图3 中可以看到流向速度沿着中心线缓慢下降，靠近壁面时骤然下降直至壁面流向速度为0，在壁面后方产生回流区，随后速度突然上升至约0.7 倍的入口流向速度并趋于平缓。在柱体后方上游区域，流向速度u1/Uin与前人实验及模拟的结果吻合较好，在方柱后方下游区域，本文结果与Tao 等[31]（Rein=1 200）以及Portela 等[35]（Rein=3 900）的数值模拟结果类似，结果落在前人结果组成的合理区间范围内。

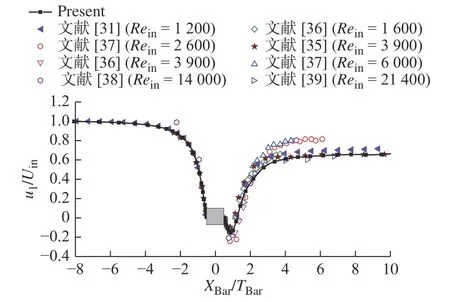
图3 无量纲平均流向速度在中心线的流向演化Fig.3 Streamwise evolution of the normalized mean streamwise velocity u1/Uin along the centerline

为了进一步验证本文的数值结果是否可以准确模拟单方柱后方的尾流，本文还与进一步比较验证了流场中的单点二阶统计量。图4 给出了中心线上3 个方向的无量纲均方根速度其中仿真结果与Portela 等[35]的结果吻合。本文的数值结果相比于Tao 等[31]（Rein=1 200）的直接数值模拟结果，两者结果在柱体前方区域类似。在方柱后方下游区域，本文的在峰值处略高于Tao 等[31]的直接数值模拟结果，但在峰值过后结果吻合良好，在峰值过后略低于Tao 等[31]的直接数值模拟结果，在峰值过后低于Tao等[31]的直接数值模拟结果，但与Portela 等[35]的结果较为接近，在合理区间范围内。由于本文使用的是大涡模拟方法，而Tao 等[31]使用的是直接数值模拟方法，直接数值模拟与大涡模拟相比对于空间分辨率需求很高，因而计算量大、耗时多，对计算资源消耗较高，对计算机内存依赖性强，精度会更为准确，但本文的数值结果与Tao 等[31]也较为接近，可见本文的计算结果在保证数值模拟结果准确性的同时可节约一定的计算资源。

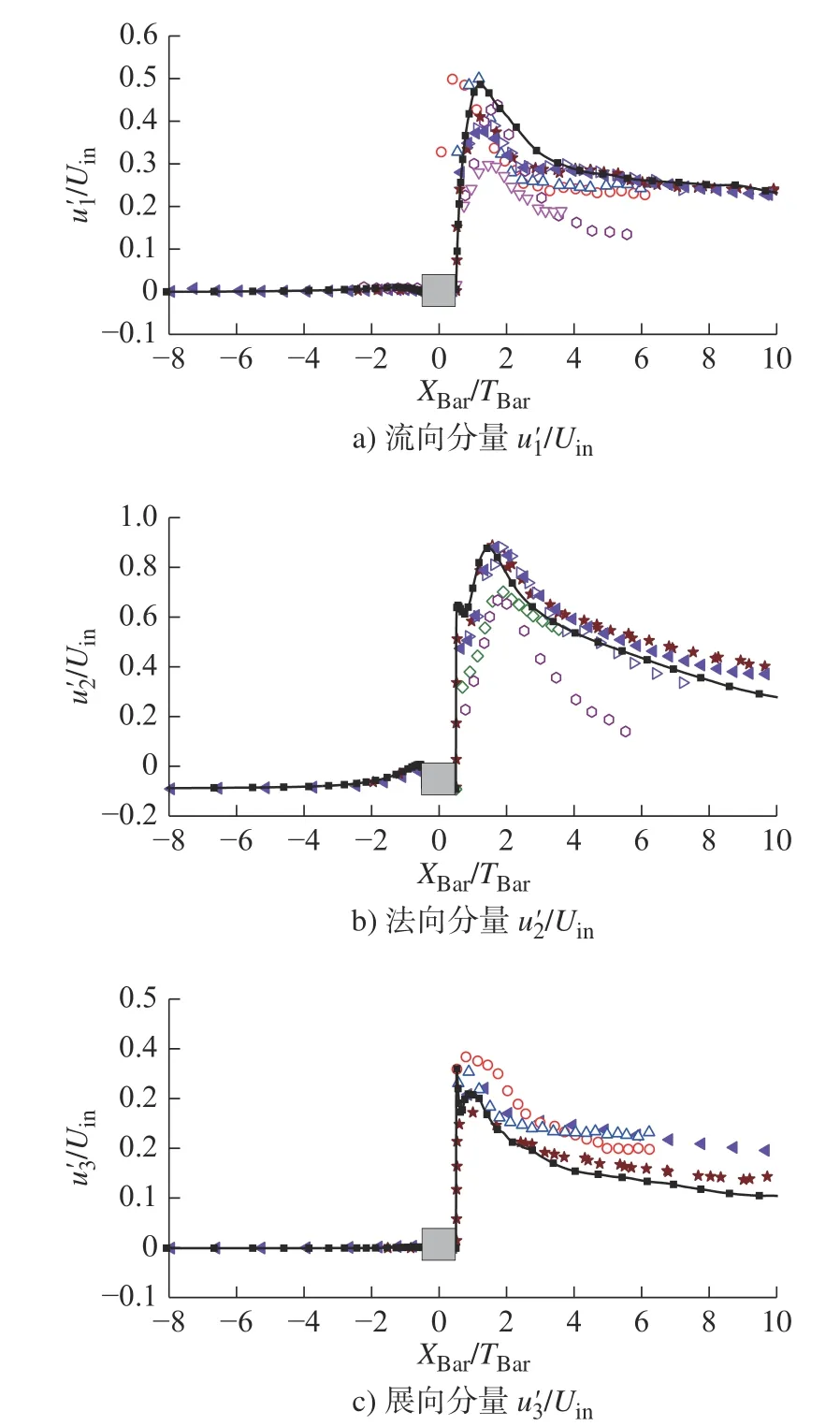
图4 均方根速度沿中心线的流向演化Fig.4 Streamwise evolution of all three rms velocities along the centerline

方柱后部涡脱落会在方柱表面引起周期性压力波动变化，进而诱导远场气动噪声。本文计算了表征流动周期性的相似准则：斯特劳哈尔数St=fL/Uin= 0.122。在当前入口雷诺数下Rein= 104，斯特劳哈尔数计算结果接近文献[36]研究结果（St≈0.13）。

图5 为不同雷诺数下的平均阻力系数CD，文献[31, 35, 40-41]表示数值结果，文献[42-45]表示实验结果。图5 表明，雷诺数Rein=104时，平均阻力系数CD落在前人结果的合理区间范围内，进一步验证了本文计算结果的正确性。

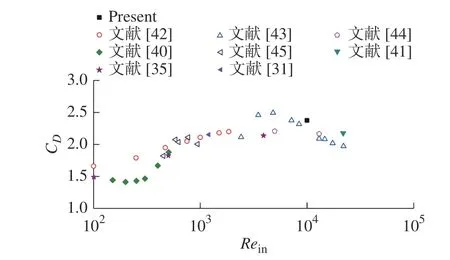
图5 不同雷诺数Rein 下的平均阻力系数CDFig.5 Mean drag coefficient CD at different Rein

此外，本文计算了方柱表面的平均压力系数CP分布，即

式中：P为当地压力；Pin为入口压力； ρ为流体密度；Uin为入口速度。图6 为单方柱A-B、B-C、C-D 和D-A 这4 个面的平均压力系数CP分布，A-B、C-D面位垂直于流向的面，B-C、D-A 面位平行于流向的面。文献[35, 41]表示数值结果，文献[46-48]表示实验结果。图6 表明平均阻力系数CP结果与前人的研究结果一致，进一步证实了本文所使用的流场计算方法可以很好的预测固体表面的涡脱落现象。

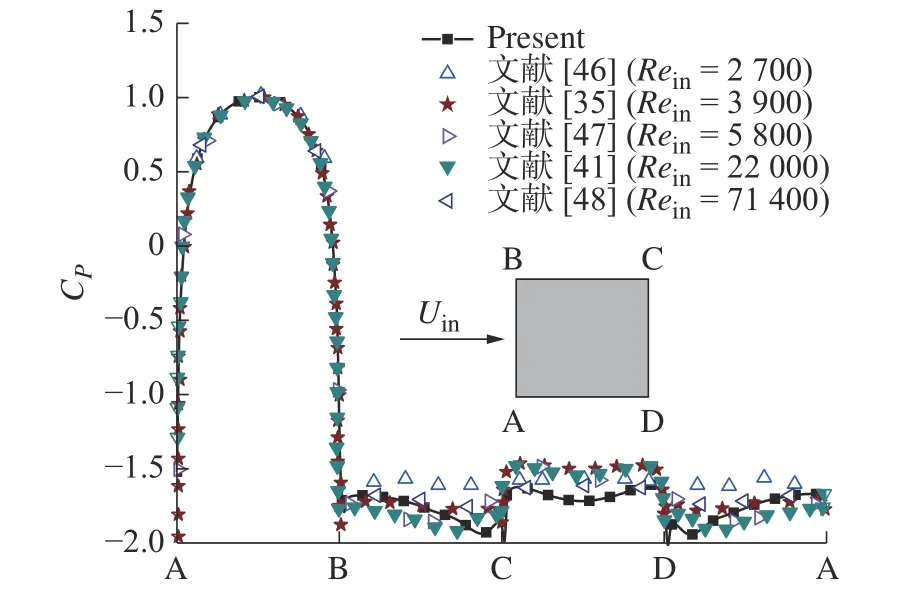
图6 单方柱4 个面上的平均压力系数CP 分布Fig.6 Distribution of the mean pressure coefficient CP over 4 sides of a single square cylinder

图7 为不同雷诺数Rein下升/阻力系数均方根值之比，其中文献[35, 40-41]表示数值结果，文献[43]表示实验结果。从图7 中可以看出，本文结果十分接近Portela 等[35]的预测结果，说明达到捕捉表面压力脉动的精度要求。

图7 不同雷诺数Rein 下的平均阻力系数与平均升力系数均方根值之比Fig.7 The ratio of the mean drag coefficient to the mean lift coefficient rms at different Rein

本小节计算了单方柱绕流的各项速度及压力指标以验证所采用数值方法的正确性，首先计算了流向平均速度及3 个方向的均方根速度在中心线上的流向演化，其次计算了斯特劳哈尔数、平均阻力系数、升/阻力系数均方根值之比以及单方柱表面的压力系数分布，验证结果显示仿真结果与前人的实验及数值结果相吻合，证实了本文所使用流场计算方法的可靠性。

2.2 噪声仿真方法验证

本文采用简化后的时域解公式（式（2））对声场进行计算。在本课题组前期研究[49]中对串列双圆柱绕流的噪声进行了数值仿真，使用了3 套不同精细程度的网格计算了串列双圆柱绕流在某一观测点处的噪声频谱分布，3 个算例所对应的网格数分别为238 万、665 万和478 万，计算结果与Langley 研究中心[50]在静流设施（Quiet flow facility, QFF）以及基础空气动力学研究（Basic aerodynamic research,BART）风洞中的实验结果相吻合，如图8 所示，其中算例3 是在算例1、2 基础上对网格所做相应改进，吻合度较高。本文采用的噪声仿真方法与前期串列双圆柱绕流气动噪声研究相同，保证了本文所使用声比拟方法的可靠性。

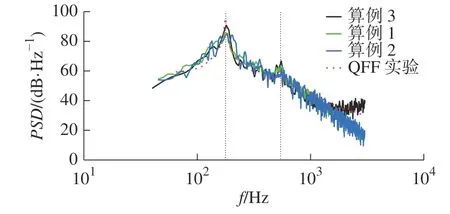
图8 观测点处的声压级功率谱密度Fig.8 Power spectral density of sound pressure level at observation points

3 计算结果与分析

3.1 湍流统计特性

在本节中将讨论规则和分形布置方柱绕流的湍流场特性，包括二维瞬时涡量、速度梯度张量第二不变量Q值瞬时等值面以及X-Y平面的平均流向速度、均方根速度和平均压力。

图9 为在任意选定展向位置Z处的无量纲瞬时涡量场，其中红色表示高涡量值≥5，蓝色表示低涡量值≤0.1。在图9 中可以清楚的看到对于两种情况的尾流，在方柱后方上游区域均呈现出高度间歇性。流体空间间歇性是指流体在空间中的状态呈现非均匀性，主要包括速度、压力、涡量等的非均匀性，而随着尾流向下游区域发展，由于各尾流间相互作用，涡量场逐渐变得均匀，空间间歇性减小。

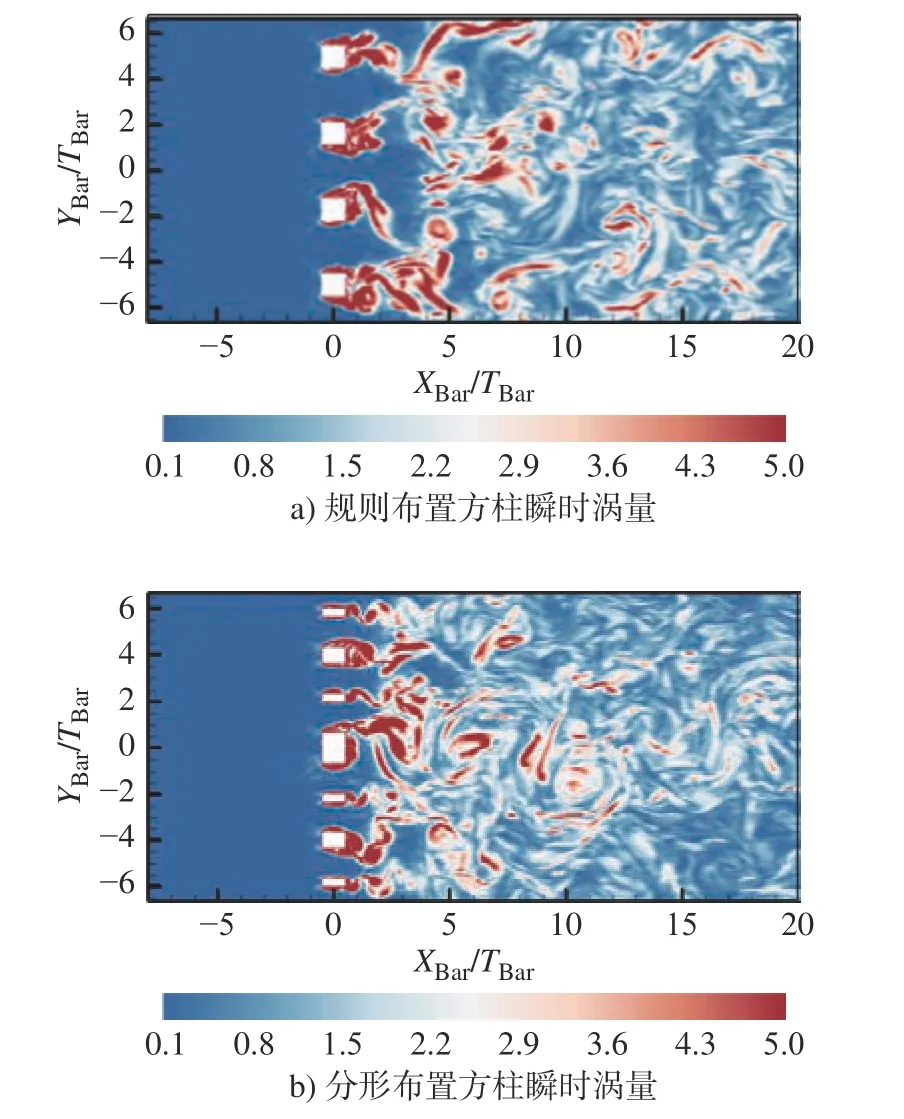
图9 X-Y 平面上的瞬时涡量等值面云图Fig.9 Contour plots of the magnitude of instantaneous vorticity in the X-Y plane

图9 的瞬时涡量场为二维瞬时云图，为了更加清晰地说明规则和分形布置的尾流涡结构，在此利用速度梯度张量第二不变量Q准则对流场进行可视化处理。图10 为与图9 相同时刻下的Q值瞬时等值面图，其中=1，颜色代表无量纲瞬时流向速度u1/Uin。图10a）表明在规则布置方柱流场中，相邻柱体后方的涡呈反相位脱落；图10b）表明在分形布置方柱流场中，涡脱落行为较为不规则。

图10 Q 值瞬时等值面图（ =1）Fig.10 Instantaneous isosurfaces of Q-value (=1)

除了尾流的瞬时涡结构外，本文研究了平均流向速度场和均方根速度场。图11 为X-Y平面上的无量纲平均流向速度场u1/Uin云图。随着向下游发展，规则布置方柱流场趋于均匀分布，而分形布置方柱流场中仍能观察到最大尺寸柱体后方的大尺度尾流的影响。

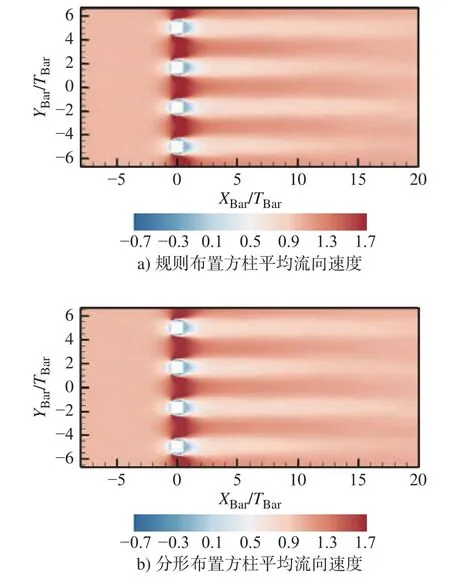
图11 无量纲平均流向速度场u1/Uin云图Fig.11 Contour plots of the normalized mean streamwise velocity field (u1/Uin)

图12 为X-Y平面上的无量纲均方根速度场云图。从图12a）中可以看出规则布置每个方柱后产生的均方根速度分布相似，图12b）显示分形布置3 种尺度的方柱后产生不同的均方根速度分布，最大尺度方柱后部的湍流强度最大。

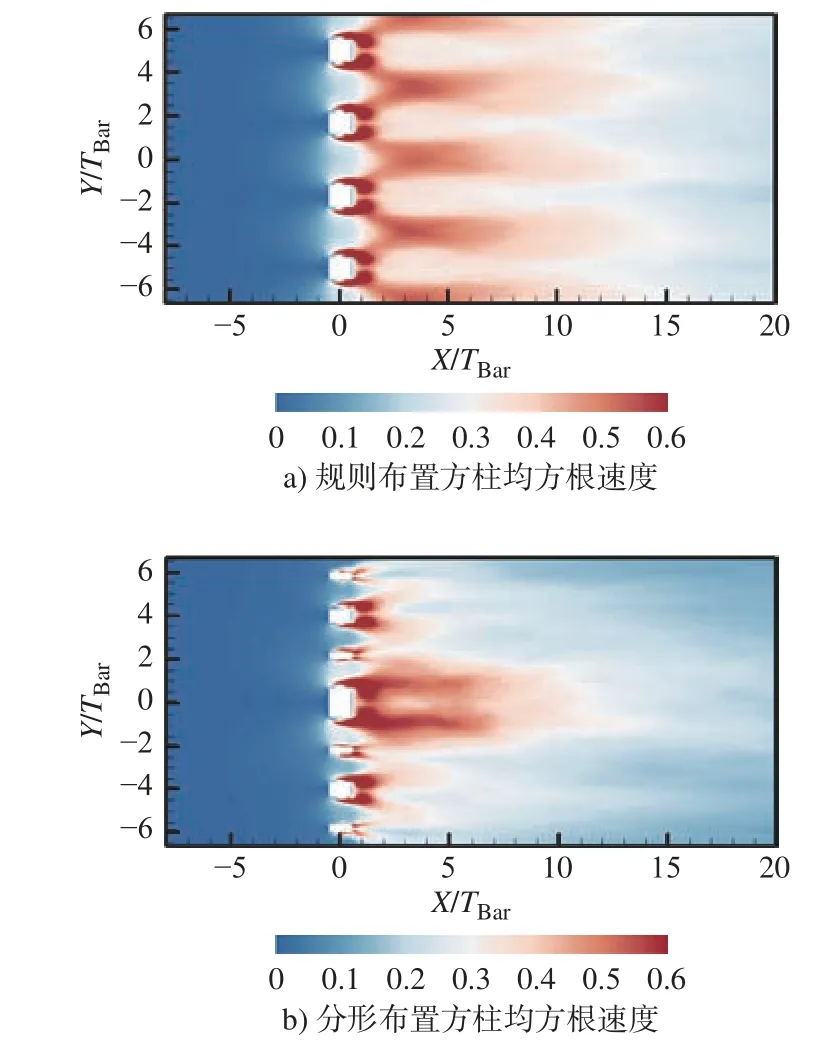
图12 无量纲均方根速度云图Fig.12 Contour plots of the normalized RMS velocity ()

图13 为X-Y平面上的无量纲化平均压力场（P-Pin）/（）云图。图13a）显示规则布置中各方柱后部的低压区分布相似，随着向下游发展，各方柱后方压力恢复速度相当。图13b）表明不同尺度方柱后的压力场分布不同，最大尺寸柱体后的压力恢复速度最慢。上述发现与平均流向速度场分布的结果相呼应。

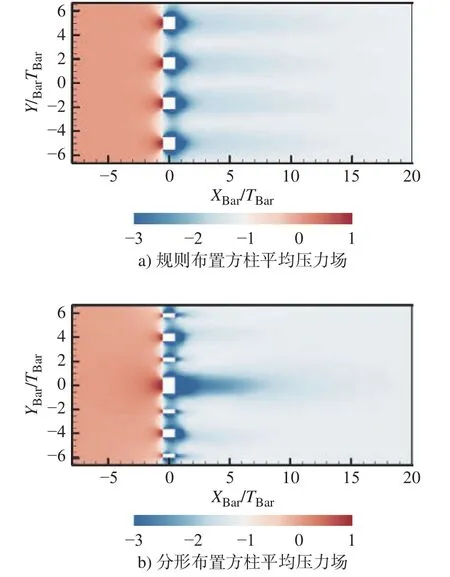
图13 无量纲平均压力场（P-Pin）/（）云图Fig.13 Contour plots of the normalized mean pressure field(P-Pin)/()

3.2 法向分布特性

图10 表明规则布置和分形布置方柱的平均速度流场有较大区别，为了进一步研究两者速度场之间的异同，本文给出了无量纲平均流向速度和法向速度在选定的5 个流向位置（XBar/TBar=2, 5, 10, 15,20）处的法向分布，见图14 和图15。由图14 可得，两种布置方柱在上游区域同时存在着类似射流（u1/Uin＞1）和类似尾流（u1/Uin＜1）的流场特性。值得关注的是，在下游远场区域，规则布置方柱的流向速度分布有趋于均匀分布的趋势，而分形布置方柱在下游区域仍能显示出明显的尾流分布特征。

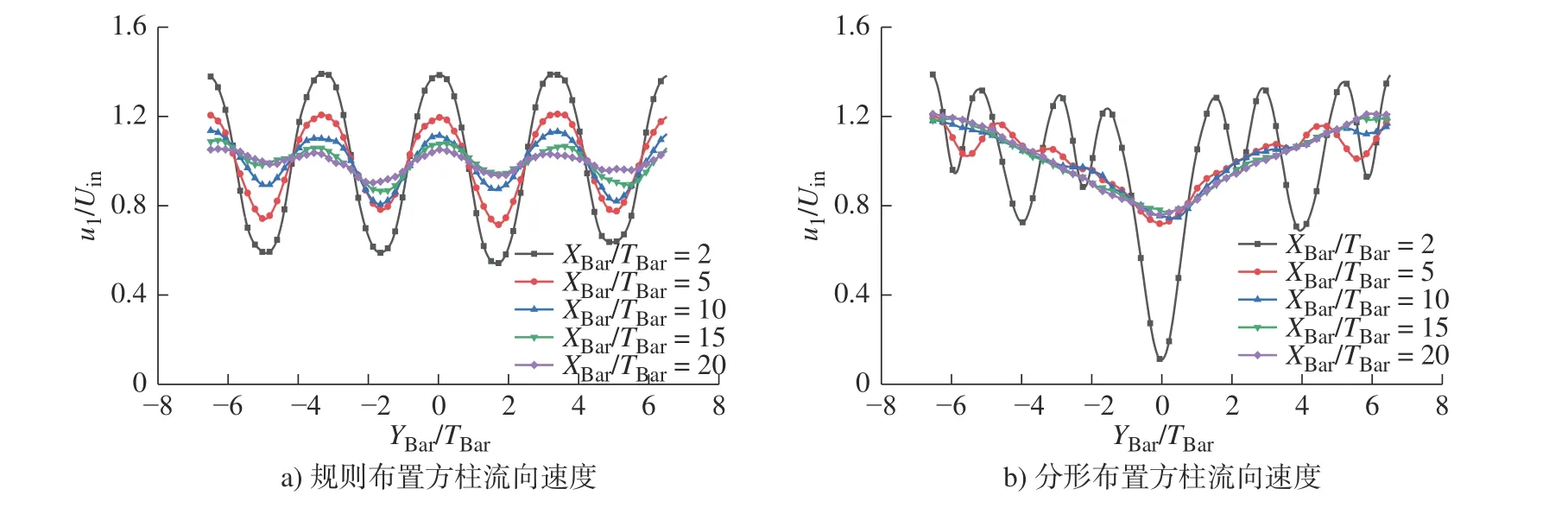
图14 无量纲化平均流向速度u1/Uin 的法向分布Fig.14 Vertical distribution of the normalized mean stream- wise velocity u1/Uin

从图15 中可以看出，在尾流的上游区域（XBar/TBar=2），两种布置方柱都表现出强烈的法向运动。在上游区域（XBar/TBar=2），柱体后方的尾流存在着正负交替的法向速度分布，促使流向速度的法向分布趋于平滑（见图13）。在XBar/TBar≥5 之后，由于流速在Y方向的平均梯度（即法向运动驱动力）变小（见图14），导致两种布置方柱后方尾流的法向运动变得不明显。

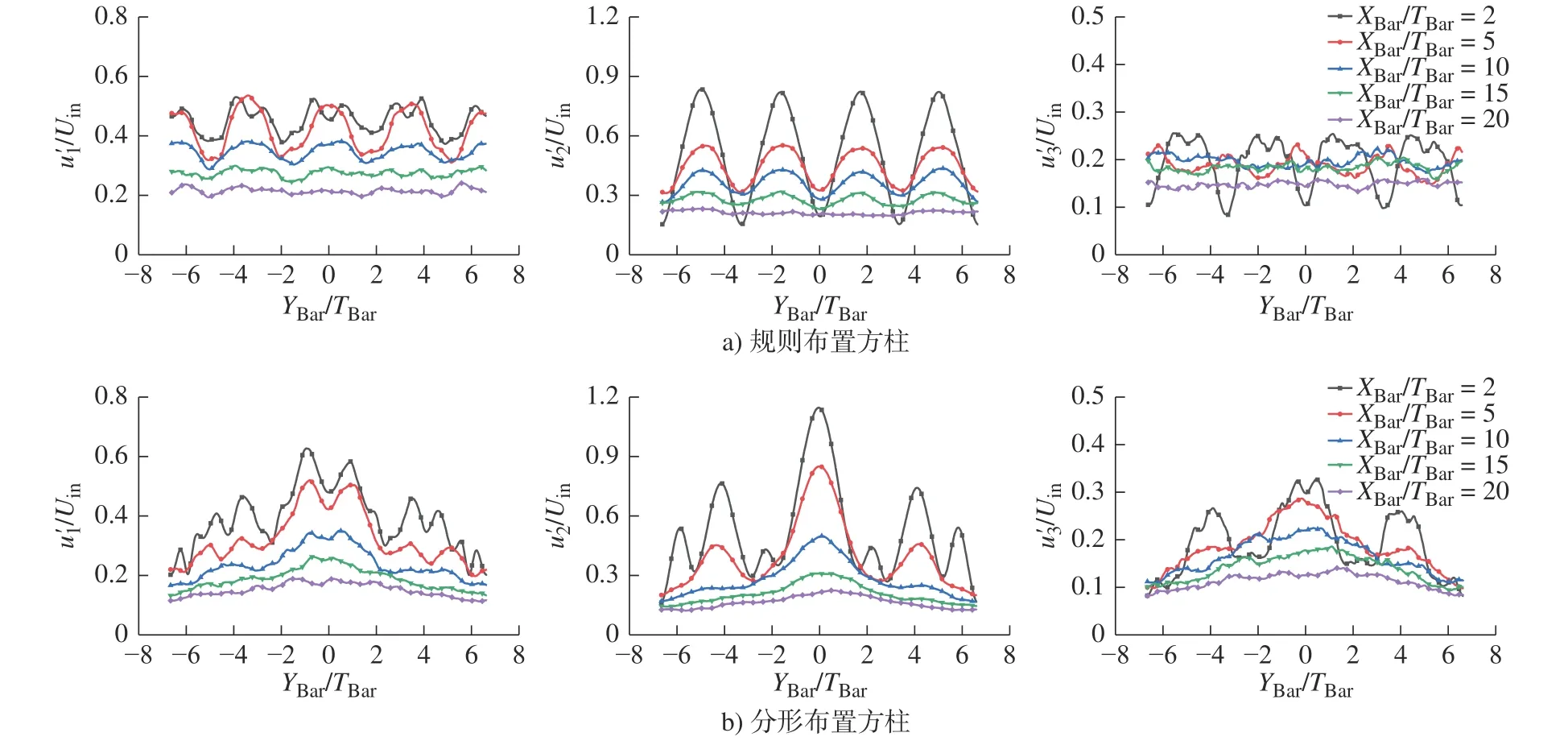
图16 无量纲速度均方根值（）的法向分布Fig.16 Vertical distribution of the normalized mean squares velocity ()

综上所述，在上游区域（XBar/TBar=2），两类流场均呈现出较强的间歇非均匀性。在下游区域（XBar/TBar≥15），分形布置流场中仍然能观察到大尺寸柱体对流向速度的影响，而该区域的法向速度和均方根速度在法向上趋于均匀分布。

3.3 旋涡脱落统计特性

多柱体绕流场中的重要特征是存在涡脱落以及涡之间的相互作用。本小节将对相关的重要问题（例如柱体的涡脱落频率、涡脱落相位关系、相位锁定的涡脱落行为以及分形布置对于规则布置能否改变相干涡结构等）进行讨论。

图17 为规则布置方柱的升/阻力系数时间演化曲线。图中升力系数CL和阻力系数CD的初始时刻（t=0）相同且为任意选定。图17a）表明在规则布置方柱中4 个方柱的涡脱落周期相同，各柱体之间存在旋涡脱落锁定，即相邻柱体的涡呈反相位脱落，其峰值大小同样保持一致。也就是说，对于任意的一个方柱，当它的升力系数CL为最大值时，其相邻方柱的升力系数为最小值。从图17b）中可以看出在规则布置方柱中，相邻方柱的阻力系数随时间演化似乎是锁定的，即阻力系数呈同相位变化。

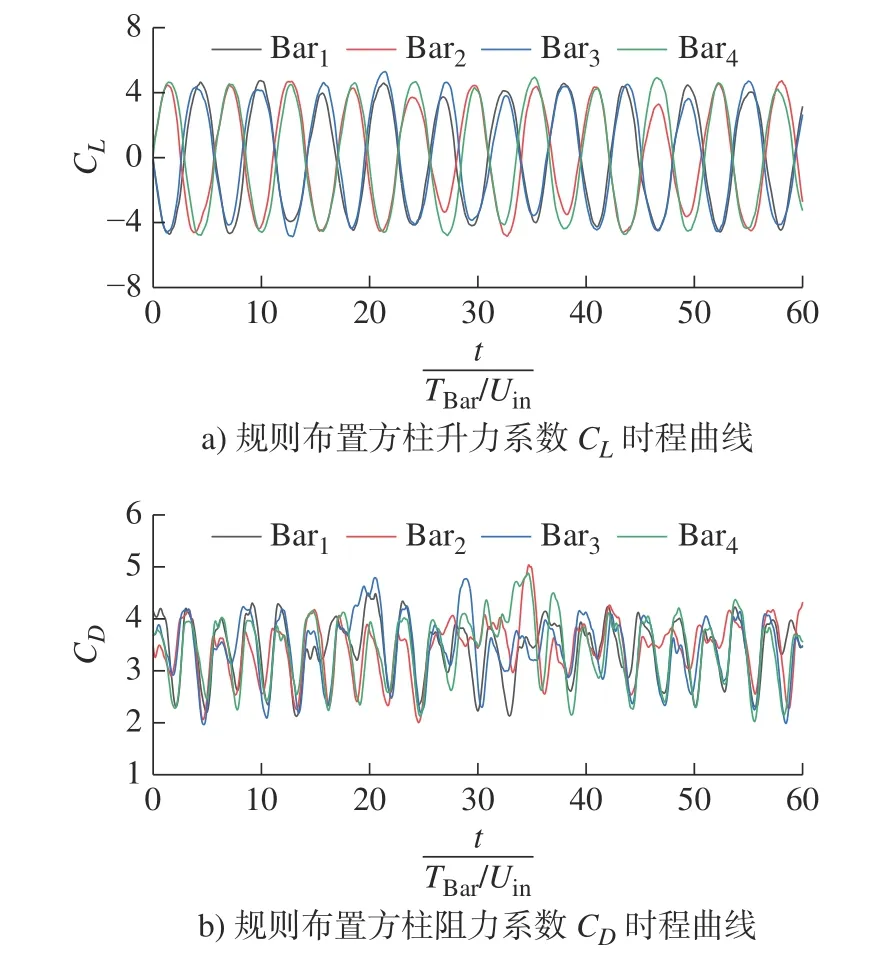
图17 规则布置4 个方柱的升力系数CL 和阻力系数CD时程曲线Fig.17 Time trace curves of the lift coefficient CL and the drag coefficient CD behind four cylinders for the regular array

为了定量的评估涡脱落行为，本文对7 × 104个时间步（对应规则布置方柱约48 个涡脱落周期）的升/阻力系数时间演化数据进行分析，通过快速傅里叶变换，得到相应的功率谱密度。由于在规则布置方柱中，4 个方柱的升/阻力系数变化相似，涡脱落周期相同。因此，在图18 中只给出了一个任意选定方柱的升/阻力系数的功率谱密度，两条垂直虚线为fTBar/Uin=0.176 和0.352。图18a）为规则布置方柱的升力系数CL频谱，主峰对应的斯特劳哈尔数为St=0.176。相比较于单方柱绕流（St=0.122），规则布置中的尾流相互作用提升了旋涡脱落频率。图18b）为规则布置方柱的阻力系数CD频谱，主峰对应的斯特劳哈尔数为St=0.352，对应升力系数斯特劳哈尔数的两倍。

图18 规则布置方柱中选定方柱的升力系数CL 和阻力系数CD 功率谱密度Fig.18 Power spectral density of the lift coefficient CL and drag coefficient CD of the chosen square cylinders for the regular array

Zheng 等[8]研究了3 个并列方柱的升力系数频谱，其3 个柱体的旋涡脱落频率分别为St=0.172,0.183, 0.172。由于存在旋涡脱落的相位滞后，导致其频谱中出现一个表征更大尺度运动的次级峰（St=0.011）。然而，本研究中规则布置各相邻方柱之间的升力系数相位锁定，因此在频谱上未观察到显著的次级峰现象。

图18 为多尺度分形布置方柱的升力系数CL和阻力系数CD的时间演化曲线。由于分形布置方柱Y轴中心对称，故选取了对应于图1b）中分形布置方柱的下半区域柱体（即Bar1、Bar2、Bar3和Bar4）的统计结果进行展示。

从图19 中可以看出，分形布置方柱后方的旋涡脱落相关性较低，不同尺度柱体的涡脱落周期有明显差异。同样对分形布置方柱的涡脱落行为进行定量评估，将7 × 104个时间步的升/阻力系数时间演化数据进行快速傅里叶变化，得到分形布置方柱的功率谱密度。

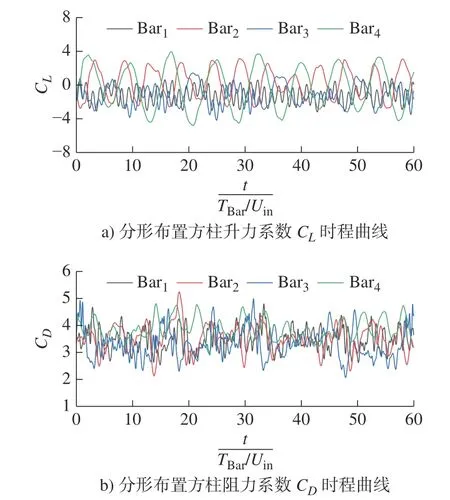
图19 分形布置方柱升力系数CL 和阻力系数CD 时程曲线Fig.19 Time trace curves of the lift coefficient CL and the drag coefficient CD of square cylinders for the multiscale array

图20 为分形布置方柱中选定方柱的升/阻力系数频谱，图20a）中3 条虚线为相应柱体的涡脱落频率，分别为fTBar/Uin=0.141, 0.192, 0.793，图20b）中3 条虚线表示两倍的柱体涡脱落频率，分别为fTBar/Uin=0.282, 0.384, 1.586。从图20a）中可以看出，多尺度的分形布置方柱产生的涡脱落频率不同，大中小3 个尺度柱体的涡脱落频率分别为fTBar/Uin=0.141, 0.192, 0.793。在升力系数频谱中，由于相邻柱体尾流间的影响，各柱体的涡脱落过程会导致在相邻柱体的频谱中出现对应的峰值。图20b）显示阻力系数频谱在相应柱体的两倍涡脱落频率处未存在明显峰值。上述发现表明，分形布置方柱产生的尾流间相互作用会对柱体阻力产生显著的影响，尤其是最小尺度柱体。

图20 分形布置方柱中选定方柱的升力系数CL 和阻力系数CD 功率谱密度Fig.20 Power spectra density of the lift coefficient CL and the drag coefficient CD of the chosen square cylinder in the multiscale case

图21 为规则布置和分形布置各方柱体的平均阻力系数CD。根据面积权重计算可得规则布置和分形布置方柱的平均阻力系数分别为3.475 和3.677。因此，在雷诺数Rein=104下，两者的平均阻力系数大致相等，分形结构并不会明显改变平均阻力系数。

图21 规则布置和分形布置各方柱体的平均阻力系数CDFig.21 Mean drag coefficient CD of different square cylinders for the regular array and the multiscale array

3.4 气动噪声特性

图22 给出了规则布置方柱和分形布置方柱位于r/TBar=32 处的远场噪声声压级（Sound pressure level, SPL）指向分布图，其中r是与观测点相同的X-Y平面上离坐标原点的距离。声压级指向性可由各点瞬时声压的均方根计算得到。

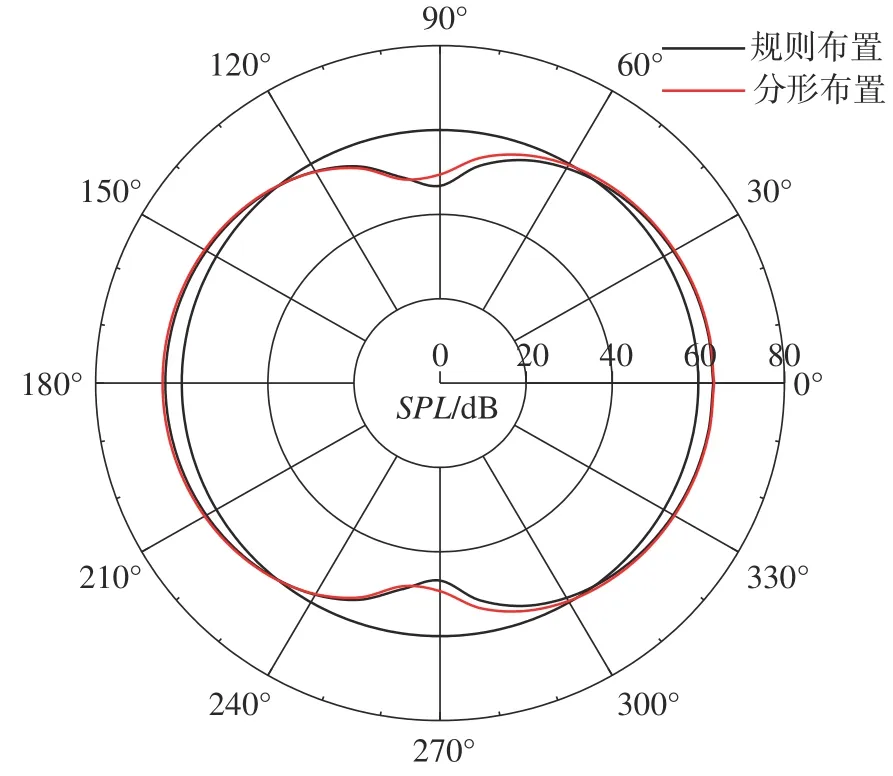
图22 远场声压级指向分布图（r/TBar=32）Fig.22 Directivity of SPL at r/TBar=32

图22 显示了规则布置方柱呈现偶极子特性，且与来流方向平行的位置处声压级最大，与来流垂直方向的位置处声压级最小。而对于分形布置方柱，其指向性分布大致与规则布置方柱相同，也呈现偶极子分布特性，但声压级最小值略偏于来流垂直方向。总体而言，分形结构对远场噪声的指向性分布影响不大。

本文选取坐标点（0, 32TBar, 0）作为观测点计算远场气动噪声特性。图23 为规则布置和分形布置方柱在选定观测点处不同柱体引起的瞬时声压随时间演化曲线。从图23a）中可以看出，在规则布置方柱中，Bar1～ Bar4的时程曲线变化与升力系数变化规律相似；图23b）表明分形布置方柱中Bar1～ Bar7产生的噪声则混乱无序。

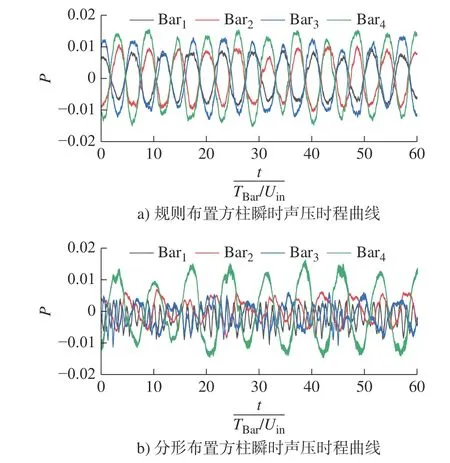
图23 规则与分形布置方柱在选定观测点（0, 32TBar, 0）处不同柱体引起的瞬时声压随时间变化曲线Fig.23 Time variation curves of the instantaneous acoustic pressure of different square cylinders at the observation point(0, 32TBar, 0) for the regular array and the multiscale array

图24 为规则布置和分形布置方柱在选定观测点（0, 32TBar, 0）处的噪声功率谱密度（Power spectral density, PSD），其中垂直虚线分别表示fTBar/Uin=0.141, 0.176, 0.192 和0.793。从图24 中可以看出，规则布置方柱的噪声功率频谱在低频段只有一个峰值（St=0.176），而分形布置方柱分别在高、中、低区段产生3 个峰值（St=0.141, 0.192 和0.793）。低频峰值为大尺寸柱体产生，中频峰值为中尺寸的柱体产生，高频峰值为最小尺寸柱体产生（见图20）。这是由于规则布置方柱只存在单一尺度的旋涡脱落，而分形布置存在不同尺度的旋涡及其相互作用。

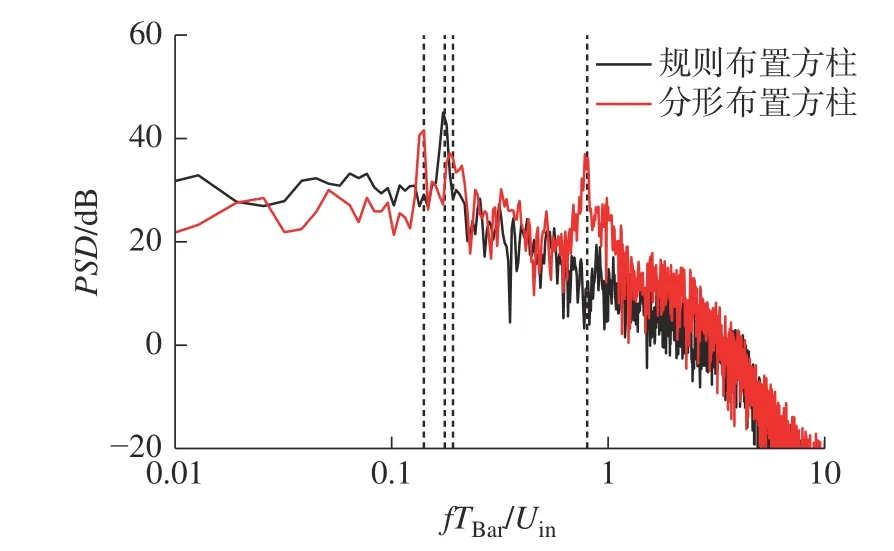
图24 规则布置和分形布置方柱在选定观测点（0, 32TBar, 0）处的声压级功率谱密度Fig.24 Power spectral density of the sound pressure level at the receiver point (0, 32TBar, 0) for the regular array and the multiscale array

上述频谱分析表明，规则及分形布置方柱的声压级功率谱密度与对应的升力系数频谱密切相关。图24 表明分形布置方柱的高频能量大于规则布置，说明分形布置能够将低频声压转化为高频声压。