计及表面残余应力的旋转凸凹型纳米圆板失稳分析

杨勇强，杨萍，张旭乐

（1.陕西科技大学 机电工程学院，西安 710021；2.陕西科技大学 电子信息与人工智能学院，西安 710021）

随着纳米技术的发展，纳米板、管、线和薄膜等结构在微纳米机电系统中发挥着重要的作用[1-5]。其中，纳米圆板由于优异的力学和电学性能，在纳米传感器、纳米谐振器、纳米发电机等方面得到了广泛的应用。二维结构的纳米材料与传统宏观材料的相比，其强度、硬度及韧性显著提高，两者的动力学性能有很大的不同。因此，研究纳米圆板的动力学特性有十分重要的工程意义。

关于纳米圆板的动力学性能研究主要集中在表面弹性理论、非局部弹性力学和应变梯度弹性理论等方面[6-10]。其中，赵德敏等[11]考虑到表面残余应力，研究了周边固支纳米圆板的振动问题，分析了表面残余应力对固有频率和主振型的影响。Assadi 等[12]采用层合板理论，分析了考虑表面残余应力纳米圆板的各种模态固有频率。Yan[13]采用基尔霍夫板模型对压电纳米圆板的弯曲及振动模型进行了研究，该修正模型分析了表面效应和非局部弹性效应对压电纳米圆板动力学特性的影响。Liu 等[14]采用Gurtin-Murdoch 连续介质理论，分析了纳米薄板和厚板的动力学特性，并以硅铝纳米板为例，分析了残余应力和边界条件对其力学特性的影响。Malekzadeh 等[15]研究了嵌入弹性介质的层合纳米圆板在初始面内径向应力作用下的轴对称自由振动和受迫振动问题。结果表明，当纳米板的半径小于某一极限值时，采用非局部弹性理论计算的固有频率与经典弹性理论计算的固有频率有很大的不同。Mahinzare[16]和Jandaghian[17]采用非局部应变梯度理论，分析了功能梯度纳米圆板的热振动问题。Zarei 等[18]采用里兹法研究了简支和固支边界条件下锥形纳米圆板的屈曲载荷和固有频率，结果表明锥度参数对固支纳米圆板动力学特性的影响大于简支纳米圆板。

微纳米机电系统中的某些纳米圆板零件均为旋转运动状态，如旋转纳米圆盘电极、振荡器纳米圆形振子等。旋转角速度对纳米圆板动力学特性有一定的影响。但是，现有关于旋转角速度对纳米圆板振动特性影响的研究较少。另外，由于纳米制造精度的影响，纳米圆板的厚度不均匀性对动力学特性的影响也值得关注。基于此，本文考虑到表面残余应力、旋转角速度以及变厚度因素，对纳米圆板的横向振动展开研究。

1 旋转凸凹型纳米圆板横向振动方程的建立

图1 所示为旋转凸凹型纳米圆板，半径为R，角速度为 Ω，密度为 ρ。根据纳米表面理论，圆板上下表面层可视为一层薄膜，中间为固体材料，设厚度线性变化，其公式为h=，其中m为变厚度系数，如果m＜0，则为凸型圆板；如果m＞0，则为凹型圆板。

图1 旋转凸凹型纳米圆板Fig.1 Rotating convex and concave circular nanoplate

根据Young-Laplace 方程，上下表面层和固体层之间存在着压力差，压力差p[11]为

式中：w为板的横向位移； τ为表面残余应力参数。圆板单位长度的弯矩Mr和扭矩Mθ为：

根据薄板小挠度理论和哈密顿原理，弹性旋转圆板的运动微分方程为

式中：Nr和Nθ为单位长度的中面内力。

根据周边简支和固支边界条件，求得周边简支和固支圆板的中面应力[19-20]为：

将式（1）、式（2）、式（4）和式（5）代入式（3）得

则无量纲凸凹型纳米圆板的运动微分方程为

2 复特征方程的建立

旋转凸凹型纳米圆板的振型方程为4 阶微分方程，可采用微分求积分法降阶来求解。微分求积分法可将高阶微分方程变成以节点处的函数值为未知数的一组代数方程组。旋转凸凹型纳米圆板振型方程节点数选取N=13，节点划分方法为

利用微分求积法离散式（8），得

周边固支边界离散形式为：

周边简支边界离散形式为：

圆心处边界条件离散形式为：

式（10）和边界条件式（11）～式（13）构成复特征方程，可表示为

式中： [I]为单位矩阵；矩阵[K]包含无量纲角速度c、变厚度系数m以及无量纲表面残余应力参数g。

3 复特征方程的建立

3.1 数值方法的有效性验证

当无量纲系数m=0，c=0，g=0时，式（8）退化为无旋转弹性小挠度薄圆板的横向轴对称自由振动问题。计算简支和固支边界条件下的圆板横向自由振动的前2 阶固有频率，与文献[21]的解相比较见表1。由表1 可知：本文解与已知解相一致，证明了微分求积法的有效性。

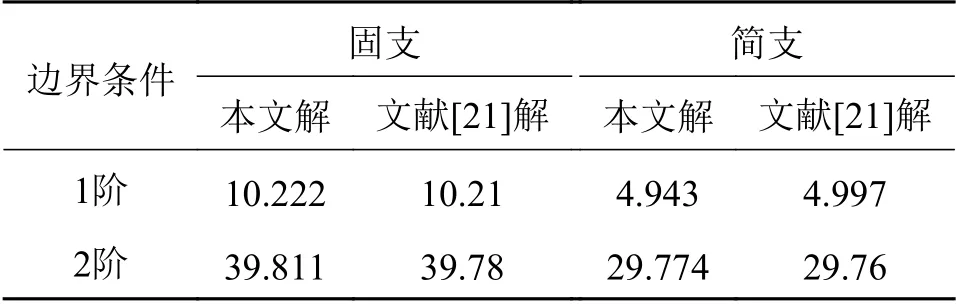
表1 弹性圆板的固有频率与已有解比较Tab.1 Comparison between natural frequency of elastic circular plate and its known solutions

研究表面残余应力对旋转纳米圆板振动特性的影响，数值分析采用的材料相关参数为[11,22]：E=177.3GPa，µ=0.27，R=6 μm，h=100 nm，τ0=0～1 N/m。无量纲表面残余应力参数g包含纳米圆板尺寸参数，根据上述参数计算，g的取值为2、4 和6。

3.2 周边固支纳米圆板

图2 为变厚度系数m取不同值时，无量纲表面残余应力参数g=3，周边固支凸凹型纳米圆板第1 阶无量纲复频率 ω随无量纲角速度c变化图。当无量纲角速度c=0时，第1 阶固有频率随着m的增大而增大，说明凹型纳米圆板的第1 阶固有频率大于凸型纳米圆板的第1 阶固有频率。随着无量纲角速度c的增加，无量纲复频率实部Re(ω)为正值并呈现减小趋势。当c增大到某一定值时，Re(ω)=0，而虚部Im(ω)分为正负两支，表明凸凹型纳米圆板发生第1 阶发散失稳现象，对应的无量纲角速度c为纳米圆板的临界发散角速度。随着变厚度系数m取值由-0.2 增大至0.2，周边固支纳米圆板的临界发散角速度减小，说明凸型圆板的稳定性不如凹型圆板。

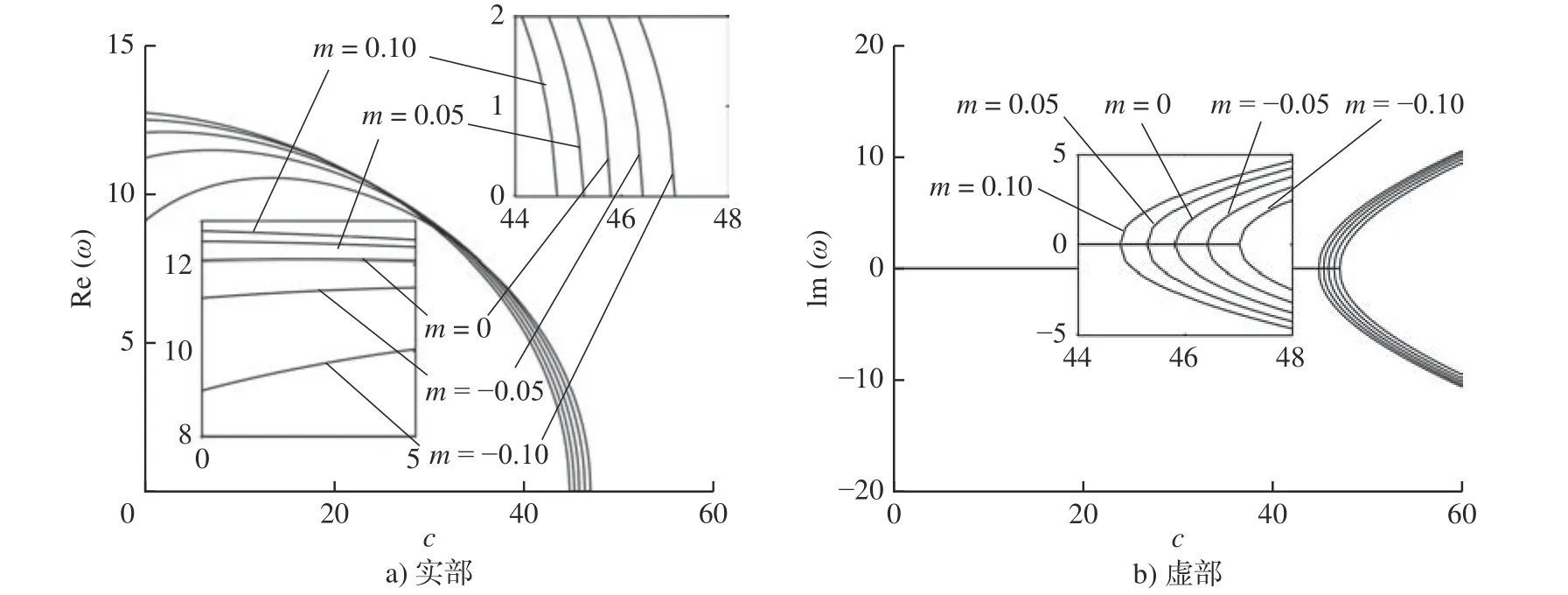
图2 第1 阶无量纲复频率 ω与无量纲角速度 c的关系曲线（固支，g=3）Fig.2 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless angular speed c (clamped edge, g=3)

图3 为变厚度系数m= -0.05，无量纲表面残余应力参数g=2、4、6，周边固支变厚度纳米圆板第1 阶无量纲复频率 ω随无量纲角速度c的变化图。可以看出，当无量纲角速度c增加到某一定值时，纳米圆板发生发散失稳现象。随着无量纲表面残余应力参数增大，稳定区域内的第1 阶固有频率增大，临界发散角速度也随之增大。

图3 第1 阶无量纲复频率 ω与无量纲角速度 c 的关系曲线（固支，m = -0.05）Fig.3 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless angular speed c (clamped edge, m = -0.05)

图4 为变厚度系数m= -0.05，无量纲角速度c=60、70、80，周边固支纳米圆板第1 阶无量纲复频率 ω随无量纲表面残余应力参数g的变化图。可以看到，当无量纲表面残余应力参数g在[0,3.1]（c=60）、[0, 3.9]（c=70）、[0, 4.6]（c=80）区间时，实部Re(ω)=0，而虚部Im(ω)≠0，纳米圆板呈现发散失稳。当无量纲表面残余应力参数g＞3.1（c=60）、g＞3.9（c=70）、g＞4.6（c=80）， 实部Re(ω)＞0，而虚部Im(ω)=0，纳米圆板处于稳定状态。临界表面残余应力参数随着无量纲角速度的增大而增大。随着无量纲残余应力参数g增大，稳定区域内的第1 阶固有频率增大。

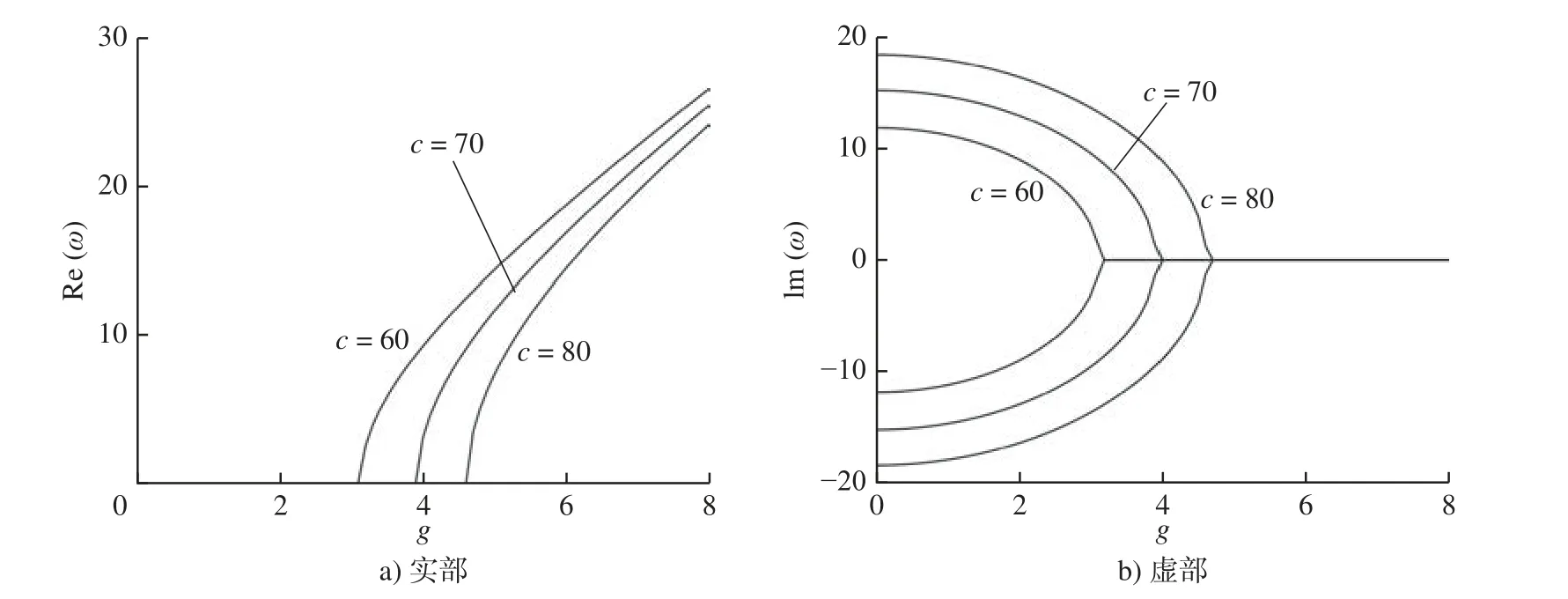
图4 第1 阶无量纲复频率 ω与无量纲表面残余应力 g 的关系曲线（固支，m = -0.05）Fig.4 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless surface residual stress g(clamped edge, m = -0.05)

3.3 周边简支纳米圆板

图5 和图6 为变厚度系数m和无量纲表面残余应力参数g取不同值时，周边简支纳米圆板第1 阶无量纲复频率 ω随无量纲角速度c的变化图。由图5和图6 可知：在其他条件一定时，随着无量纲角速度c的增加，无量纲复频率实部Re(ω)一直减小，纳米圆板在一定条件下发生第1 阶发散失稳现象。与周边固支不同的是，周边简支情况下的临界发散角速度随着变厚度系数m和无量纲残余应力参数g的增大而增大。

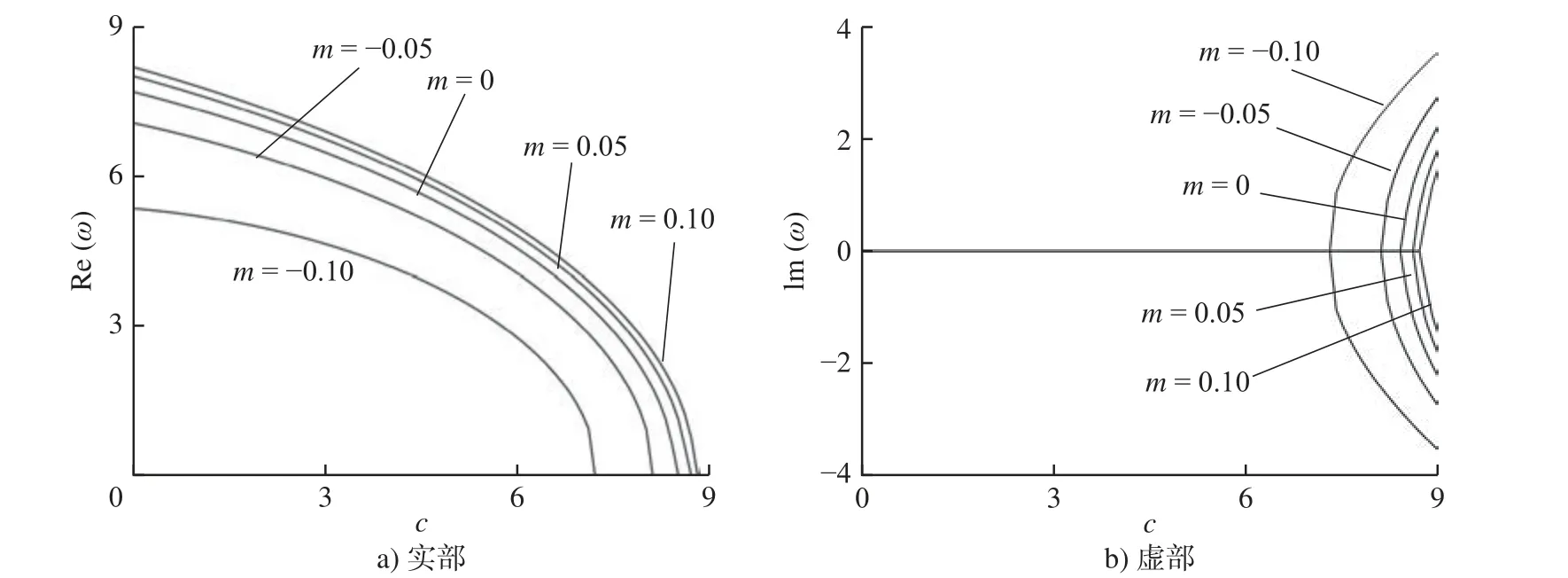
图5 第1 阶无量纲复频率 ω与无量纲角速度 c 的关系曲线（简支，g = 3）Fig.5 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless angular speed c (simply supported edge, g = 3)

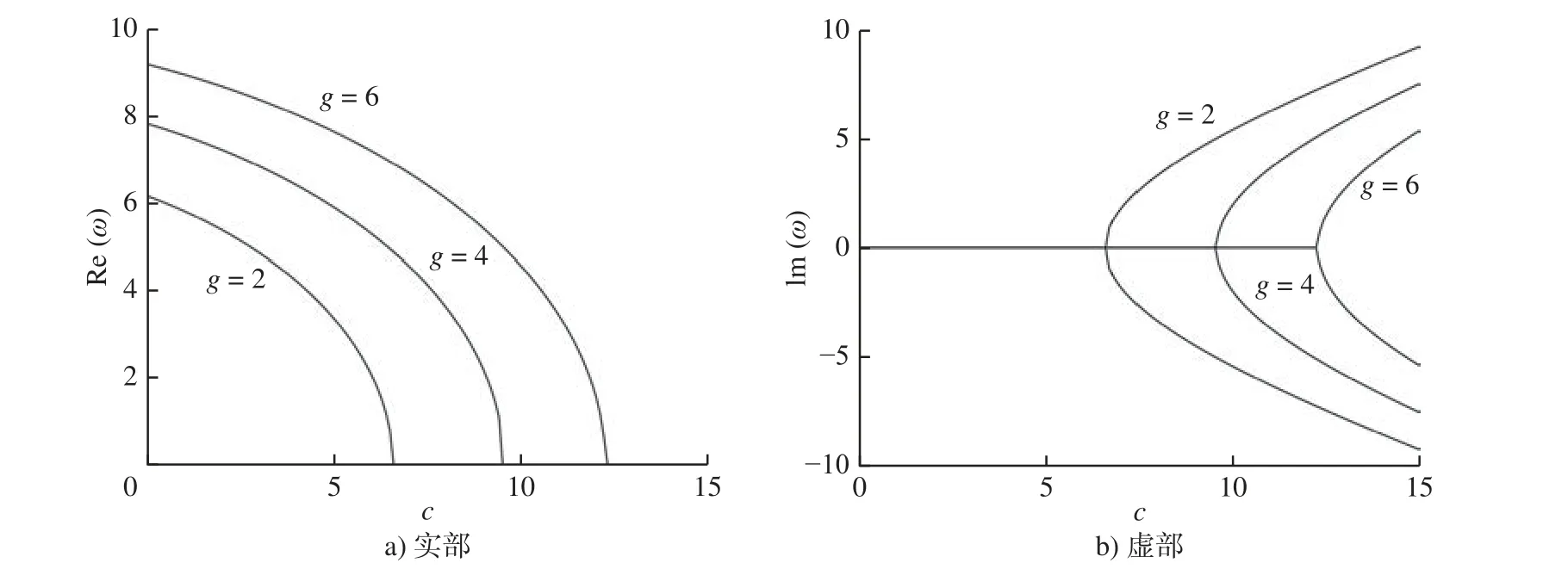
图6 第1 阶无量纲复频率 ω与无量纲角速度 c 的关系曲线（简支，m = -0.05）Fig.6 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless angular speed c (simply supported edge, m = -0.05)

图7 为变厚度系数m= -0.05，无量纲角速度c=5、10、15，周边简支纳米圆板第1 阶无量纲复频率 ω随无量纲表面残余应力参数g的变化图。可以看到，当无量纲表面残余应力参数g= 1.0（c=5）、g= 4.3（c=10）、g=8.1（c=15）时，纳米圆板发生发散失稳现象。随着无量纲角速度的增大，临界表面残余应力参数增大。

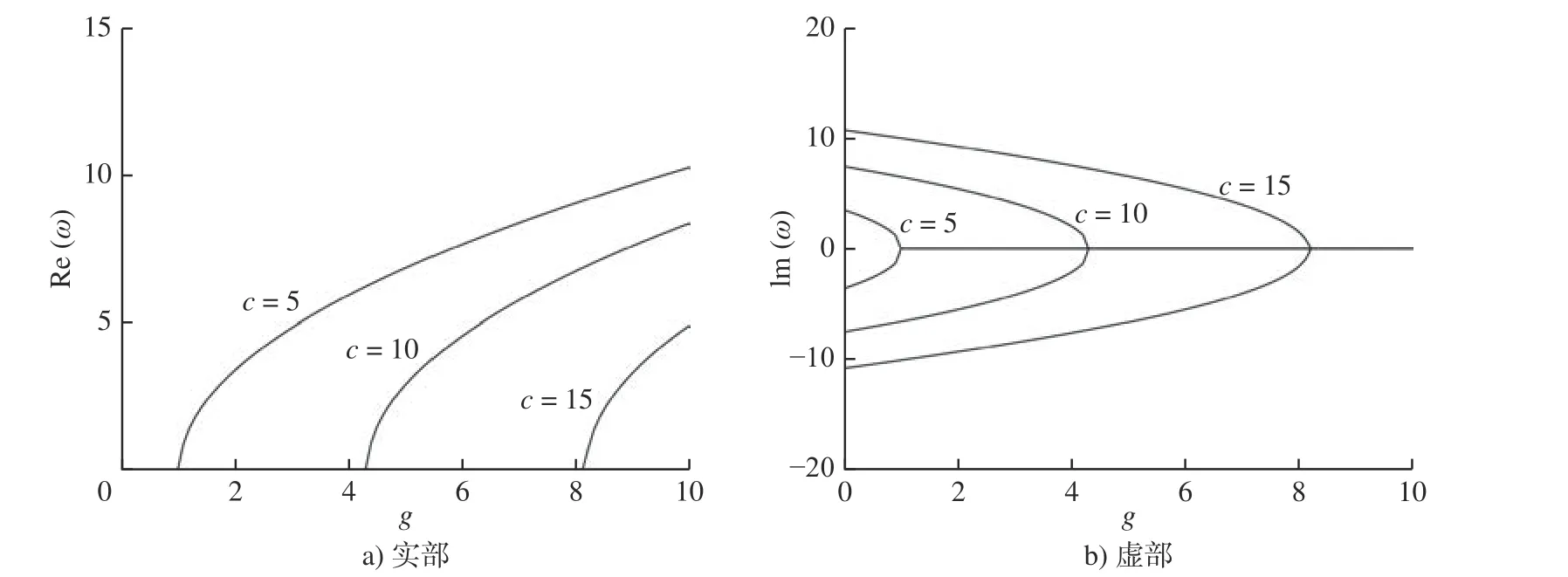
图7 第1 阶无量纲复频率 ω与无量纲表面残余应力 g 的关系曲线（简支，m = -0.05）Fig.7 Relationship curves for the first-order dimensionless complex frequency ω versus dimensionless surface residual stress g(simply supported edge, m = -0.05)

4 结论

本文分析了旋转凸凹型纳米圆板横向振动问题，讨论了旋转角速度、变厚度系数和表面残余应力参数对旋转凸凹型纳米圆板动力学稳定性的影响。

1）在周边固支和简支边界条件下，凸凹型纳米圆板发生第1 阶发散失稳现象，周边固支凹型纳米圆板的临界发散角速度小于凸型纳米圆板的临界角速度，周边简支凹型纳米圆板的临界发散角速度大于凸型纳米圆板的临界角速度。

2）在其他条件一定的情况下，纳米圆板的临界发散角速度随着无量纲表面残余应力系数的增大而增大；临界表面残余应力系数随着无量纲角速度的增大而增大。

以上分析为旋转纳米机电系统的稳定性分析提供了一定的理论基础。