考虑内外环交互作用的VSG并网振荡特性
2024-04-02李琳张晓楠李庚银蔡德福孙冠群
李琳,张晓楠,李庚银,蔡德福,孙冠群
(1.新能源电力系统全国重点实验室(华北电力大学),北京市 102206;2.国网湖北省电力有限公司电力科学研究院,武汉市 430077)
0 引 言
“双碳”战略目标下,风电光伏发电装机规模不断增大,2022年风电光伏新增装机占全国新增装机的78%[1-2]。随着新能源占比及电力系统电力电子化程度的不断提高,新能源电力系统呈现低惯量和弱阻尼特点,严重威胁电力系统的安全稳定运行[3-5]。虚拟同步控制策略通过虚拟同步发电机(virtual synchronous generator,VSG)的转子运动方程,使逆变器具备惯量和阻尼支撑能力而得到了广泛应用[6-7]。但是电力电子设备间存在多种控制回路,导致电力系统的动态行为极其复杂,给电力系统安全稳定运行带来了新的挑战[8-10]。
建立简单可靠的数学模型是分析VSG并网系统动态特性与稳定问题的基础。文献[11-12]建立VSG并网系统的全阶小信号模型,研究了内环控制参数对系统动态特性的影响,但所建立的模型阶数很高,建模和运算都极为复杂,分析难度很大。文献[13-14]基于多时间尺度的模型降阶方法,针对功率外环控制建立VSG并网系统的三阶小信号模型,但仅考虑了有功环与无功环的稳定性与稳定裕度,模型精度较低,难以覆盖系统低频段动态特性。文献[15-16]利用阻抗模型将整个系统以单一阻抗的形式来等效,但所有环节杂糅在一起,难以用于分析稳定机理。此外,奇异摄动、数值分析算法等数学手段也被广泛应用于VSG模型分析。文献[17]利用奇异摄动提取全阶模型中的慢速状态变量。文献[18]基于哈尔小波建立虚拟同步机多时间尺度模型。但这些方法无法将实际问题与物理机理联系起来,并且不具有普适性。现有文献建模过程中没有重点关注电力电子设备存在的多时间尺度动态行为,对模型分析不够全面,针对VSG中存在的多时间尺度交互现象,亟需一种简单、可靠、适用范围更广的数学模型来研究VSG并网系统稳定性。
针对VSG的稳定性研究往往着重于功率外环,而忽略内环控制的影响。文献[19]将内环简化为单位增益,仅考虑功率外环的前提下分析了惯量系数、阻尼系数等控制参数以及运行参数对系统主导振荡模态的影响。文献[20]则忽略内环控制分析了线路电感瞬变过程引起的工频振荡现象。这些研究将VSG内外环控制解耦,降低系统模型阶数简化分析,但是内环与外环间的相互作用对系统稳定性也会产生很大的影响,该方法对系统振荡特性的分析并不精确[21]。文献[22]在保证内环跟踪控制的前提下,通过补偿量实现内外环的解耦控制,降低了模型阶数,并基于阻抗模型简洁地描述了构网型变流器内环控制的阻尼效应。文献[23]提出了阻抗电路模型的概念,将系统的控制回路可视化为阻抗电路中的虚拟阻抗,通过各控制参数对虚拟阻抗间相位差的影响,揭示各控制回路之间的相互作用和耦合效应。使用阻抗模型分析时,为建立等效模型需简化一些关键控制参数的影响,并且阻抗之间的耦合关系与网络动态特性的影响交织在一起使分析困难[24]。文献[25]建立全阶状态空间方程,通过分析不同并网条件、控制参数下系统的特征根轨迹研究系统的稳定性。基于Heffron-Phillips稳定分析模型可以观察参数变化对阻尼转矩的影响,从负阻尼转矩的角度解释系统振荡的失稳机理[26]。文献[27]建立仅计及电压环的虚拟同步机的类Heffron-Phillips稳定分析模型,应用阻尼转矩法揭示虚拟转子的运动的阻尼特性。文献[28]则基于全阶小信号模型转换成类Heffron-Phillips,通过伯德图研究不同控制参数对振荡模态对应负阻尼大小的影响,但是由于新能源并网系统时间尺度较大,相互作用复杂,影响因素繁多,使得模型阶数过大,运算过程复杂。因此,亟需一种分析方法,在不舍弃关键影响因素的前提下,既简化系统模型,又能简单准确地分析内外环交互作用下VSG并网系统的稳定机理。
针对上述问题,本文选取时间常数为主导特征对VSG并网系统进行降阶,提取影响内外环交互作用的关键因素,获得考虑内外环交互作用的降阶模型,将降阶模型在平衡点处线性化得到类Heffron-Phillips稳定分析模型;基于阻尼转矩法分析了不同控制参数、运行参数下VSG并网系统的振荡特性;并分析了内外环交互作用与线路电磁暂态共同作用引入的振荡模态及其关键影响因素。最后,通过时域仿真验证了所建模型和关键影响因素分析的准确性。
1 VSG并网系统
1.1 VSG控制结构
VSG并网系统拓扑结构如图1所示。为了方便本文研究,将新能源侧用恒定的直流电压源Udc替代,变流器经LC滤波器和传输线路阻抗接入无穷大交流电网。图1中:PWM表示脉宽调制;PI表示比例-积分控制器;Rf为滤波电阻;Rg为电网电阻;Lf为滤波电感;Lg为电网电感;Cf为滤波电容;Uf,dq和Uo,dq分别为dq旋转坐标系下的逆变器输出内电势、变流器机端电压(滤波电容电压);Ug为并网点电压;If,dq为dq旋转坐标系下流通滤波电感的电流;Ig为注入电网的电流;Ifref,d和Ifref,q为电压内环控制输出的电流指令;Ufref,d和Ufref,q为电流环控制输出的电压调制指令;其余变量含义具体见下文。

图1 VSG并网系统拓扑结构
逆变器交流侧的状态方程为:
(1)
If-Ig=(sCf+jωCf)Uo=YCfUo
(2)
式中:Uo=uo,d+juo,q为变流器机端电压矢量,其中uo,d和uo,q分别为逆变器机端电压矢量在dq旋转坐标系下的d轴和q轴分量;Uf=uf,d+juf,q为逆变器输出内电势矢量,其中uf,d和uf,q分别为内电势的d轴和q轴分量;Ug=Ugcosδ-jUgsinδ为并网点电压矢量,δ=θVSG-θg为控制器dq旋转坐标系相位与电网dq旋转坐标系相位的差值;If=if,d+jif,q和Ig=ig,d+jig,q分别为逆变器侧和网侧电流矢量,其中if,d和if,q分别为逆变器侧电流的d轴和q轴分量,ig,d和ig,q分别为网侧电流的d轴和q轴分量;Zg(s)和ZLf(s)分别为线路和滤波器阻抗的矢量形式;YCf(s)为电容输出矢量形式;ω为输出角速度。
虚拟同步控制策略包含功率外环控制以及电压电流内环控制。功率外环模拟同步发电机的转子运动方程以及励磁电压方程,通过功角控制有功功率的输出,通过电压幅值控制无功功率的输出,使功率输出能够跟随给定的指令值。功率外环控制可以描述为:
(3)
式中:ωref是系统角速度参考值,其值大小为314 rad/s;J和D分别为虚拟同步机转子惯量系数和阻尼系数;kq为模拟无功调压下垂特性的系数;E和Eref分别为变流器输出电动势实际值以及功率外环输出的参考值;P和Pref分别为变流器向电网输送有功功率的实际值以及参考值;Q和Qref分别为变流器向电网输送无功功率的实际值以及参考值。
电压电流内环控制在dq坐标系下利用PI控制器实现,其目的是提高输出电压稳态精度与系统响应速度,抑制并网VSG振荡。dq坐标系下控制方程为:
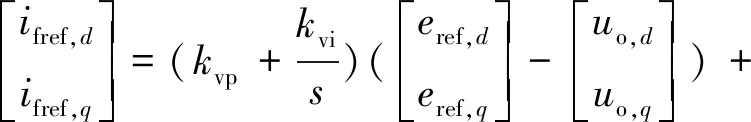
(4)
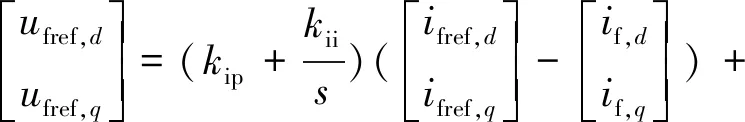
(5)
式中:Ifref=ifref,d+jifref,q和Ufref=ufref,d+jufref,q分别为电压电流内环输出的逆变器侧电流和内电势参考值,其中ifref,d、ifref,q、ufref,d和ufref,q分别为dq旋转坐标系下内环输出的相应矢量的d轴和q轴参考值;Eref=eref,d+jeref,q为功率外环输出的内电势参考值,通常取eref,q为0,则此时Eref的大小等于无功外环输出的电动势d轴参考值eref,d;kvp和kvi分别为电压内环的比例系数和积分系数;kip和kii分别为电流内环的比例系数和积分系数;Gv(s)和Gi(s)分别为电压、电流内环PI控制环节对应的传递函数;eref,dq为dq旋转坐标系下功率外环输出的变流器内电动势参考值。
考虑到流过电容的电流远小于输出电流,可忽略不计,则VSG输出功率的计算公式为:
S=P+jQ=Uf*Conj[Ig]
(6)
式中:P和Q分别为变流器输出的有功功率和无功功率;Conj[Ig]表示对电网电流矢量做共轭运算。
1.2 考虑内外环交互作用的VSG并网系统降阶模型
VSG多时间尺度控制环节如图2所示,可以看出多个控制环节导致整个系统的带宽覆盖于数Hz至数百Hz的宽频范围。本文聚焦于系统振荡频率在工频以下的振荡模态特性,选取时间常数作为主导特征对系统全阶模型进行降阶。
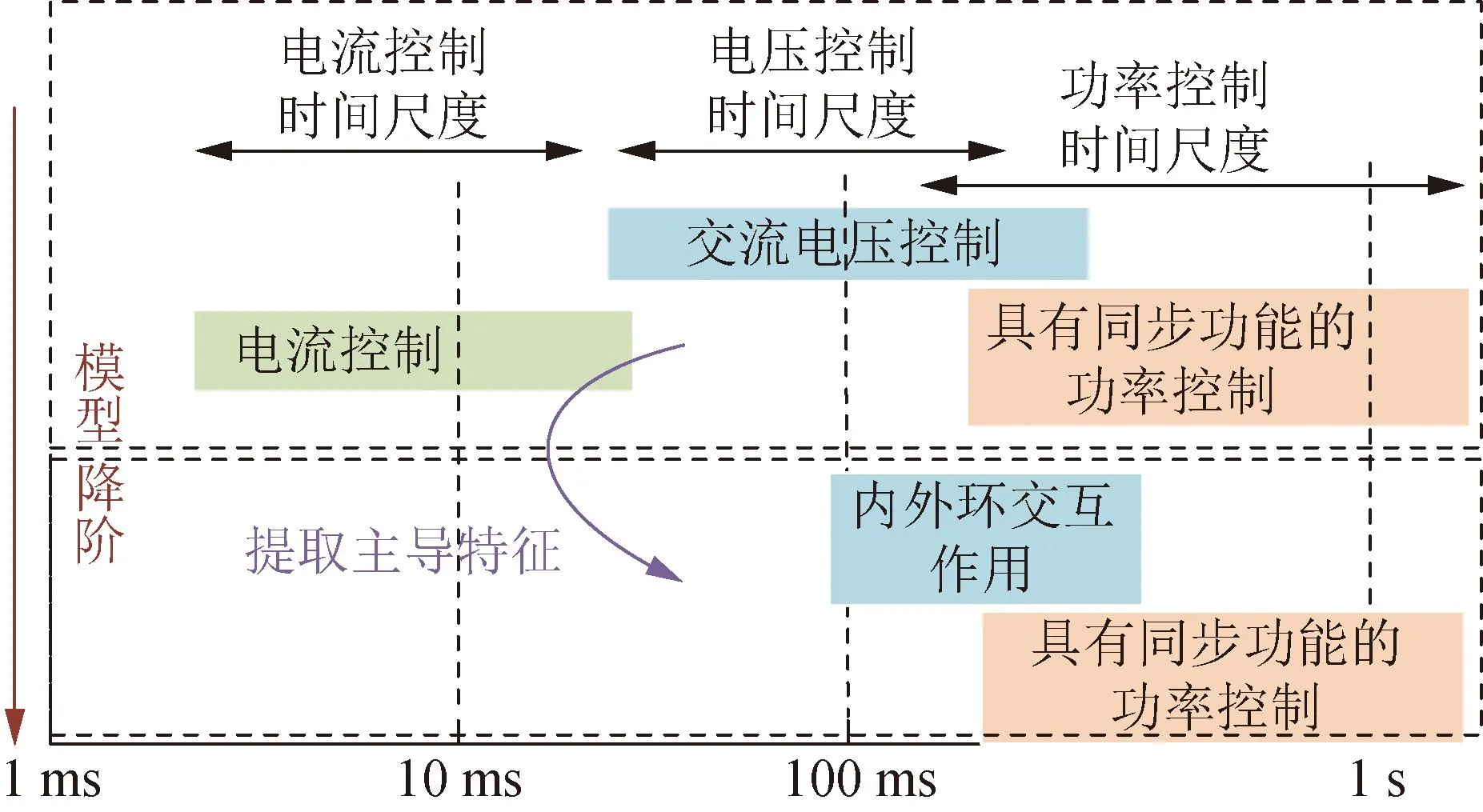
图2 VSG多时间尺度控制环节
时间常数型传递函数的一般形式为:
(7)
式中:τ和T为对应环节的时间常数,下标1和2分别对应不同的环节;ζ为阻尼比;K为开环增益;当s的上标v为正数时,表示为微分环节,当v为负数时,表示积分环节。将时间常数作为主导特征,基于时间常数对模型降阶。选定截断时间常数Tc和截断频率fc=1/Tc,对应的截断角速度ωc=2πfc,忽略Ф(s)中时间常数小于Tc和频率大于fc的环节,仅保留开环增益K和时间常数大于Tc的元素,这样降阶之后可以从Ф(s)中提取出想要重点关注的状态量而截断其他元素,降阶后的模型可以保证所研究带宽下模型的准确性。
功率外环可以用式(4)准确地描述,下文主要对内环控制所对应的传递函数模型进行降阶,联立式(2)、式(5)、式(6)可得:
(8)
对应的等值电路如图3所示,从图中可以看出内环控制等效为受控电压源以及等效输出阻抗。
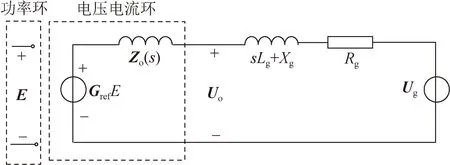
图3 全阶模型的单相等值电路
图1中流过电容的电流Ic远小于流入电网的电流Ig,可忽略不计,因此可忽略Gref(s)和Zo(s)中dq轴之间的耦合项,将式(8)简化为:
(9)
基于时间常数对上式进一步简化降阶,本文研究的是VSG并网系统的低频振荡以及次同步振荡,为了保证足够的精度,选择Tc=0.01 s作为截断时间常数[29],即截断频率fc=100 Hz,截断角速度ωc=628 rad/s,选取该时间常数能够准确描述并网系统两倍工频以下的动态特性。当0<ω<ωc时:
|Rf+sLf+Gi(s)|s=jω<<|Gv(s)Gi(s)|s=jω
(10)
此时,Gref(s)≈1,将内环控制传递函数Gv(s)、Gi(s)代入Zo(s)中可得:
(11)
电流内环带宽较大,Zo(s)中二阶环节对应的时间常数(Lf/kii,(kvpkip)/(kvikIi))远小于截断时间常数,忽略Zo(s)中的对应环节,则可以得到Zo(s)≈s/kvi。
根据式(11)可知,降阶模型把VSG内外环的交互作用等效为输出阻抗Zo(s)=Los=s/kvi对电压源的影响,等效输出阻抗的表现形式为电感Lo,因此VSG内部控制器对电网状态的延迟效应可以理解为VSG等效输出阻抗的滞后效应。VSG输出阻抗Zo(s)的大小由电压内环控制参数决定,随着电压内环积分控制参数的减小,系统等效输出阻抗Zo(s)增大。VSG并网系统的等效电路方程可以表示为:
E-Ug=[Zo(s)+Rg+sLg]Ig
(12)
式中:E为无功功率外环输出的变流器内电动势大小。
绘制等值电路如图4所示。
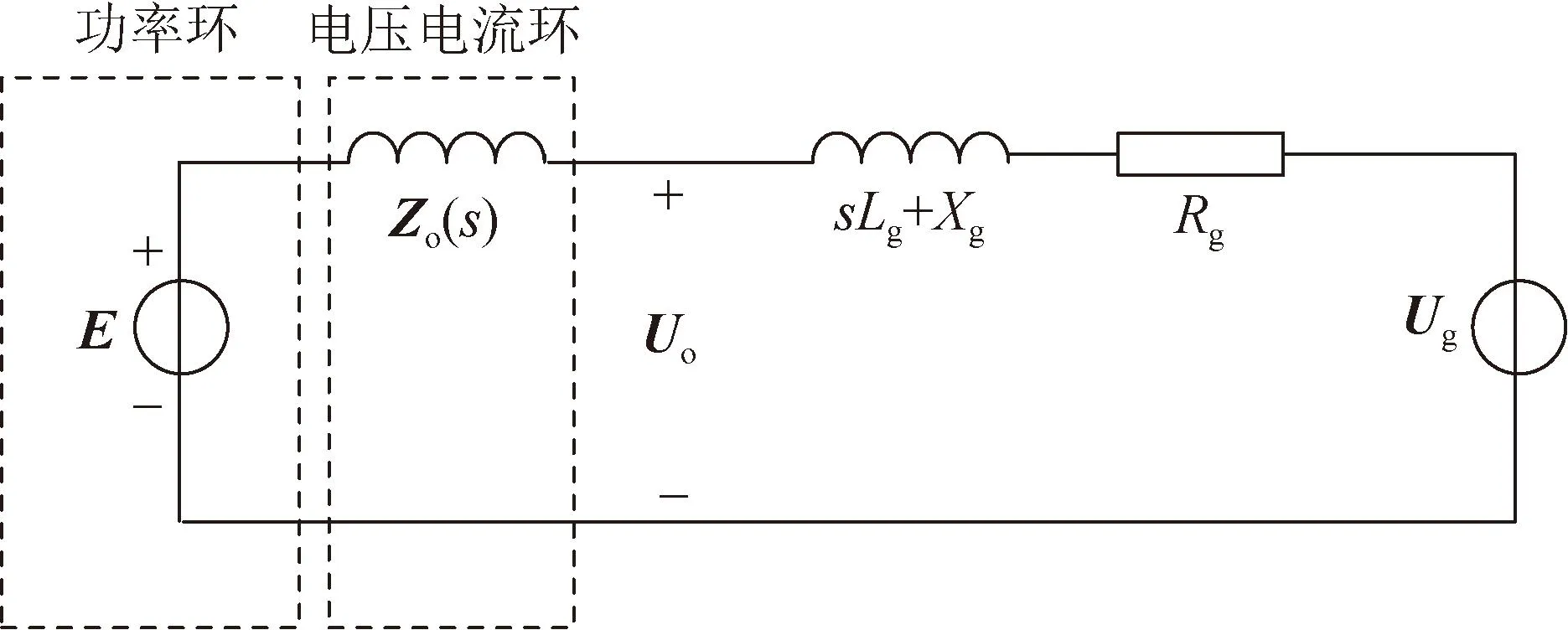
图4 考虑VSG内外环交互作用的等效电路
选取时间常数作为主导特征对模型进行降阶,使模型既可以准确地保留并网系统在对应频带范围内的动态特性,又简化了后续对系统动态特性以及稳定性的分析过程,提高了物理机制透明度。
2 VSG小信号建模
2.1 VSG小信号模型
联立式(6)、式(11)和式(12),可得VSG输出功率的表达式为:
(13)
式中:Gsd(s)=(Rg+sLg)E+sLoUgcosδ;Gsq(s)=ωLgE-sLoUgsinδ;E=|E|为变流器内电动势的模值。
将式(3)和式(12)在平衡点处线性化,可以得到VSG并网系统的小信号模型:
(14)
(15)
式中:Zo(s)=Rg+(Lg+Lo)s;Gc-δP(s)、Gc-EQ(s)分别为有功、无功外环控制前向通道传递函数;GPδ(s)、GPE(s)分别表示P-δ、P-E反馈通道的传递函数;GQδ(s)、GQE(s)表示Q-δ、Q-E反馈通道的传递函数;E0、Ug0、δ0分别为稳态工作点下逆变器的内电势、电网电压、输出功角;ΔP、ΔQ、Δδ、ΔE、Δω、Δωg分别为有功功率、无功功率、功角、内电动势、VSG输出角速度、电网角速度的小扰动分量;ωref=314 rad/s为VSG额定角速度。
根据式(13)、式(14)建立包含有功无功动态耦合的以有功功率指令值扰动为输入,有功无功功率为输出的VSG并网系统小信号模型,如图5所示。
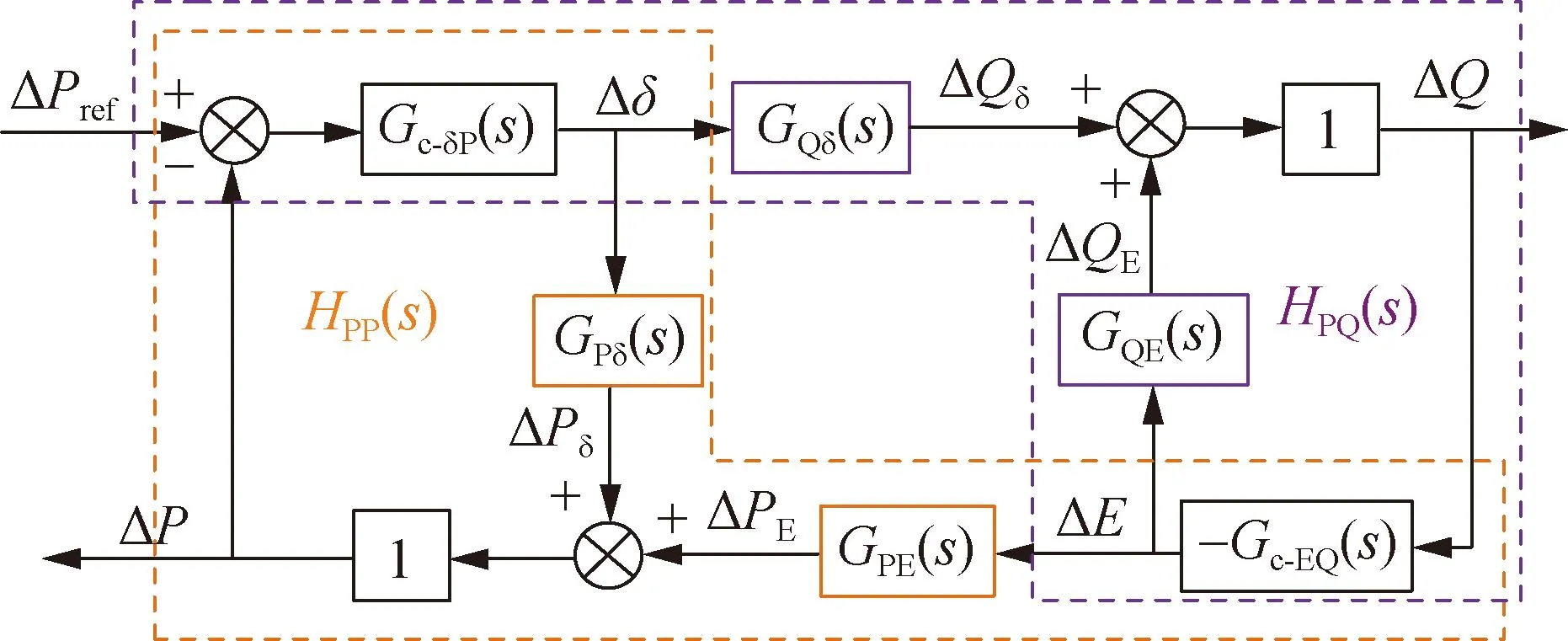
图5 VSG并网系统功率动态耦合小信号模型
根据降阶模型可知,内外环交互作用表现为电压内环积分控制参数决定的等效电感,为了进一步探究电压内环控制参数对系统振荡特性的影响,把图5所示的线性化模型变换成类Heffron-Phillips模型,反映各个控制环节对系统输出动态特性的影响,量化阻尼转矩,从阻尼转矩的视角分析振荡特性及其关键影响因素,图6所示为以有功功率参考值为输入,功角为输出,重构的VSG并网系统的小信号模型。
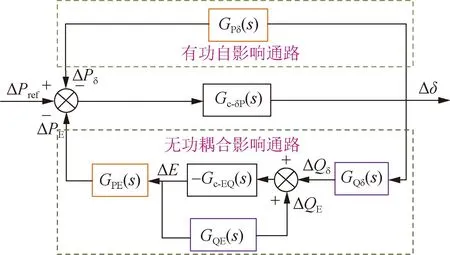
图6 功率扰动输入-功角输出的小信号模型
根据图6可以写出:
(16)
式中:ΔPE表示由于有功无功耦合导致的有功功率扰动分量。
消去ΔE,则功率耦合对应路径的有功功率可以表示为:
(17)
因此,耦合影响通路以及非耦合影响通路反馈的总电磁功率可表示为:
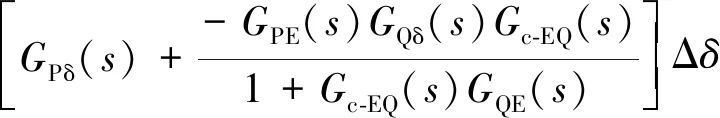
(18)
式中各传递函数根据式(14)、(15)获得,传递函数GPδ(s)和GEδ(s)分别代表各个控制环节对输出有功功率的影响,GPδ(s)与电压内环控制参数和运行参数有关,GEδ(s)还会受到无功-电压控制环节的耦合影响。
基于上述分析可以得到如图7所示的稳定分析模型。电磁转矩可以被分解为与角速度偏差同相位的阻尼转矩分量,以及与相角偏差同相位的同步转矩分量。阻尼转矩过小会导致系统发生振荡,从图中可以看出,反馈路径主要与内环控制参数、线路运行状态有关,因此可以基于该模型观察内外环交互作用和并网条件对阻尼转矩的影响来研究VSG并网系统的振荡特性。
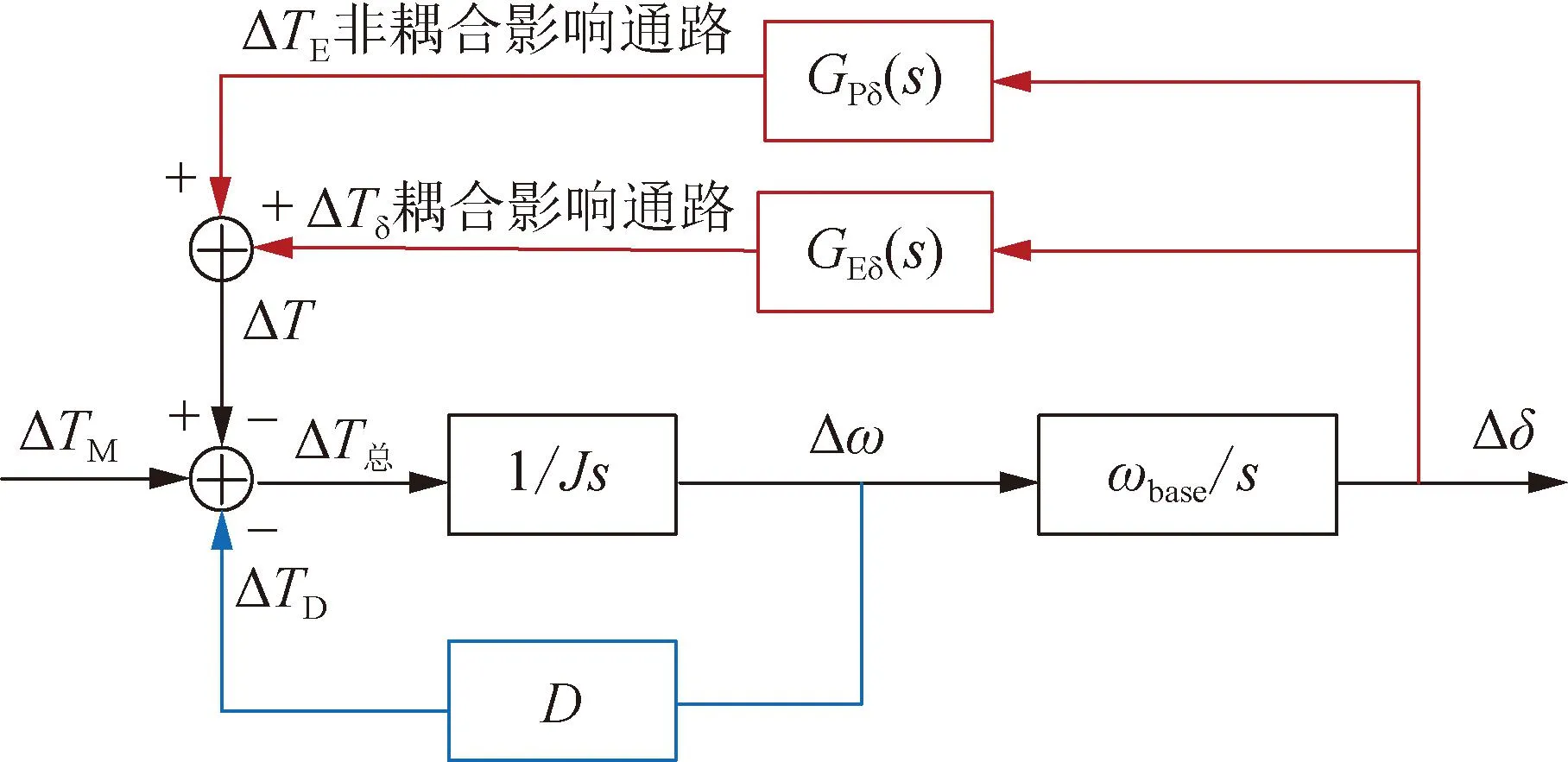
图7 基于阻尼转矩法的稳定分析模型
2.2 模型验证
为验证所提模型的正确性,图8和表1为采用附录表A1所示参数时,通过最小实现的方式求解本文建立的降阶模型的特征根,并与全阶模型特征根分布进行对比。可以看出,全阶模型包含6对共轭特征根,分布在低中高全频段范围内,本文建立的降阶模型在低频段包含两对共轭特征根,与全阶模型在低频段的两对共轭特征根基本重合,即该降阶模型可以准确描述系统在工频以下频段的动态特性,可以准确分析VSG并网系统该频段范围下的振荡特性。

表1 VSG并网系统模型特征根
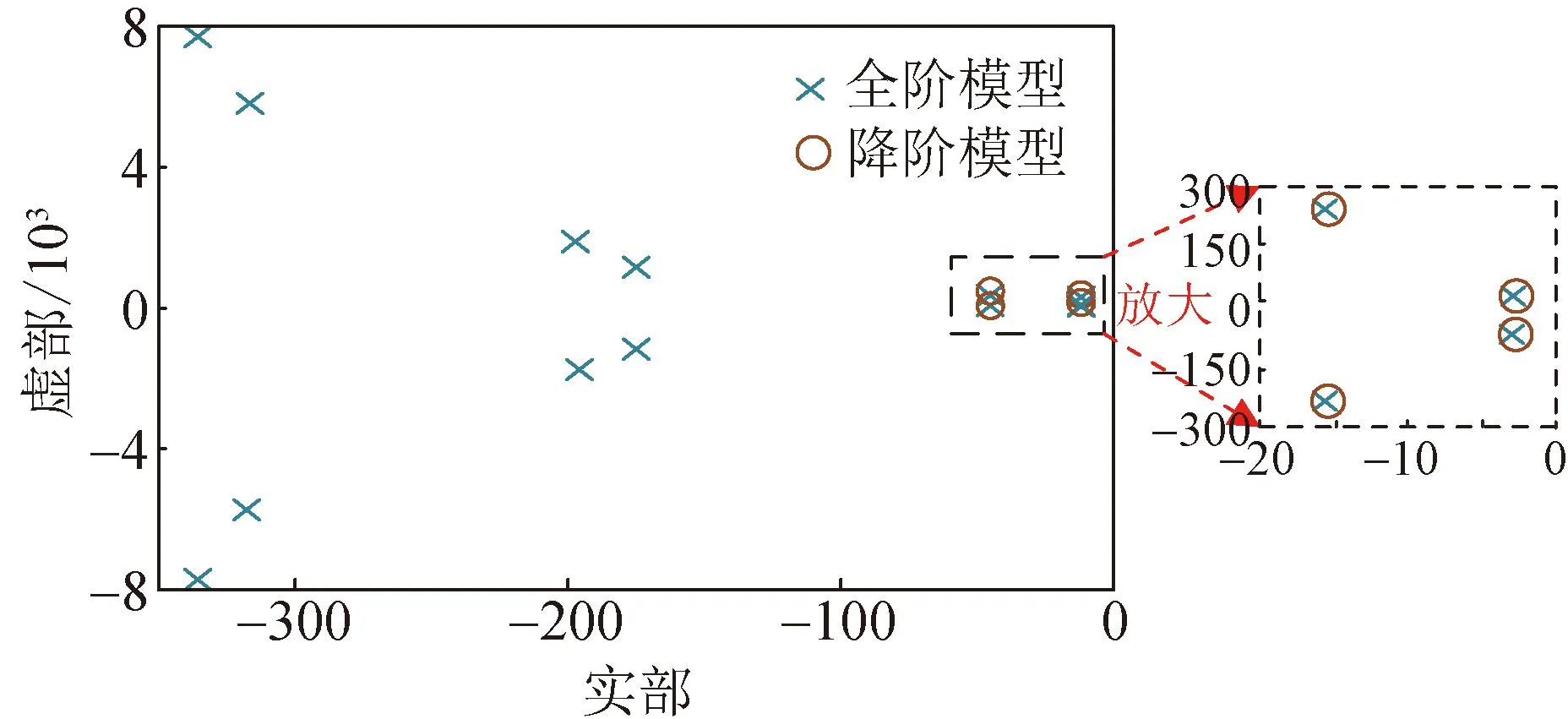
图8 降阶模型与全阶模型特征根对比
3 考虑内外环交互作用的系统稳定性分析
外环控制参数对该振荡模态的影响在大量文献中已被研究,本节则重点基于阻尼转矩法分析内环控制参数、线路运行参数对功率外环主导振荡模态稳定性的影响,并研究VSG等效输出阻抗与线路电磁暂态共同作用导致的次同步振荡机理与关键影响因素。
3.1 电压内环控制参数对振荡模态λ1,2的影响
为分析电压内环控制参数对系统振荡的影响,保持其他参数不变,改变电压内环控制参数,观察其对主振荡模态的影响。图9(a)中给出了VSG在不同电压内环比例参数下等效电磁转矩传递函数对应的伯德图,根据主导振荡频率所对应的幅值和相位可以得到对应的等效电磁转矩矢量图,如图9(b)所示。可以看出,随着电压内环比例系数的减小,等效电磁转矩幅值和相位基本保持不变,说明电压内环比例系数对系统振荡稳定性并不会产生太大的影响。
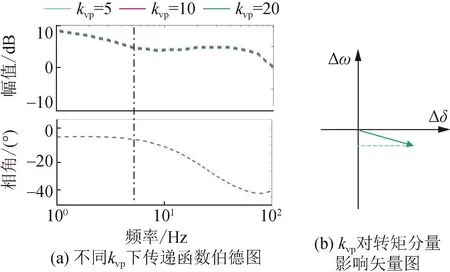
图9 电压内环比例参数对阻尼转矩的影响
改变电压内环积分系数时电磁转矩伯德图如图10(a)所示,进一步根据主导振荡频率对应的幅值和相位绘制等效电磁转矩的矢量图,如图10(b)所示,从图中可以看出随着积分系数的增大,等效电磁转矩向Δω轴负方向靠近,并且相量幅值也增大,稳定裕度减小。因此随着电压内环积分系数的增大,各个控制环节相互耦合引入的负阻尼成分增大,系统总阻尼成分减小,不利于系统的振荡稳定。
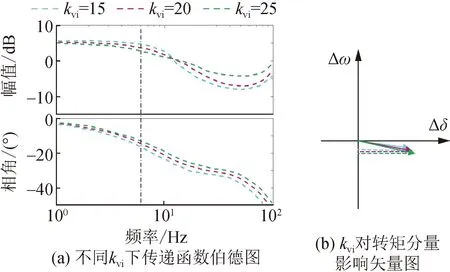
图10 电压内环积分参数对阻尼转矩的影响
上述分析也间接证明了1.2节对模型降阶处理的准确性。
3.2 线路Rg/Xg对振荡模态λ1,2的影响
研究线路运行参数对振荡动态特性的影响,改变线路电感以改变Rg/Xg,图11(a)为不同Rg/Xg下电磁转矩对应的伯德图,随着线路Rg/Xg的降低,相频特性曲线在振荡频率处相位偏移几乎一致,而幅频特性随着Rg/Xg的减小而减小。根据伯德图绘制系统振荡频率对应的矢量图,如图11(b)所示,可以看出, 随着Rg/Xg减小,负阻尼转矩也随之减小,提高了该振荡模态的稳定性。因此,由于该振荡模态主要受功率外环控制环节的影响,当Rg/Xg较大时,dq轴解耦特性被削弱,强化负阻尼效应,此时增加线路电感值,随着Rg/Xg减小,解耦性能变好,负阻尼效应被削弱,使得VSG具有较好的功率输出特性,有利于该振荡模态的稳定。
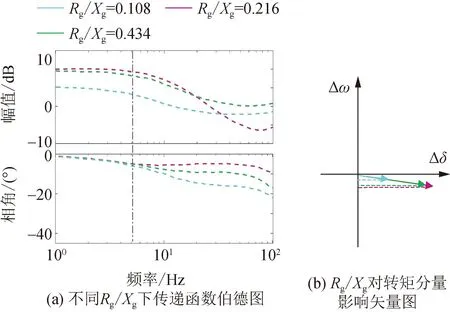
图11 线路Rg/Xg对阻尼转矩的影响
利用相对增益矩阵(relative gain array , RGA)量化有功功率和无功功率的耦合程度[30]。基于系统的动态模型,充分揭示系统在动态过程中不同频段的耦合特性。相对增益矩阵为:
(19)
式中:β11和β22分别表示有功环、无功环的自耦合系数;β12(β21)表示有功环与无功环的相互耦合系数。β11和β22越接近1,表明系统耦合度越低,相反,β12(β21)越接近1,则系统耦合度越高。绘制β12(β21)在不同Rg/Xg下的变化曲线图,如图12所示,从图中可以看出,随着Rg/Xg的减小,在主导振荡模态对应的振荡频率处系统有功、无功之间的耦合得到改善,功率输出动态特性得到优化,与图11所示的利用阻尼转矩分析结果一致。
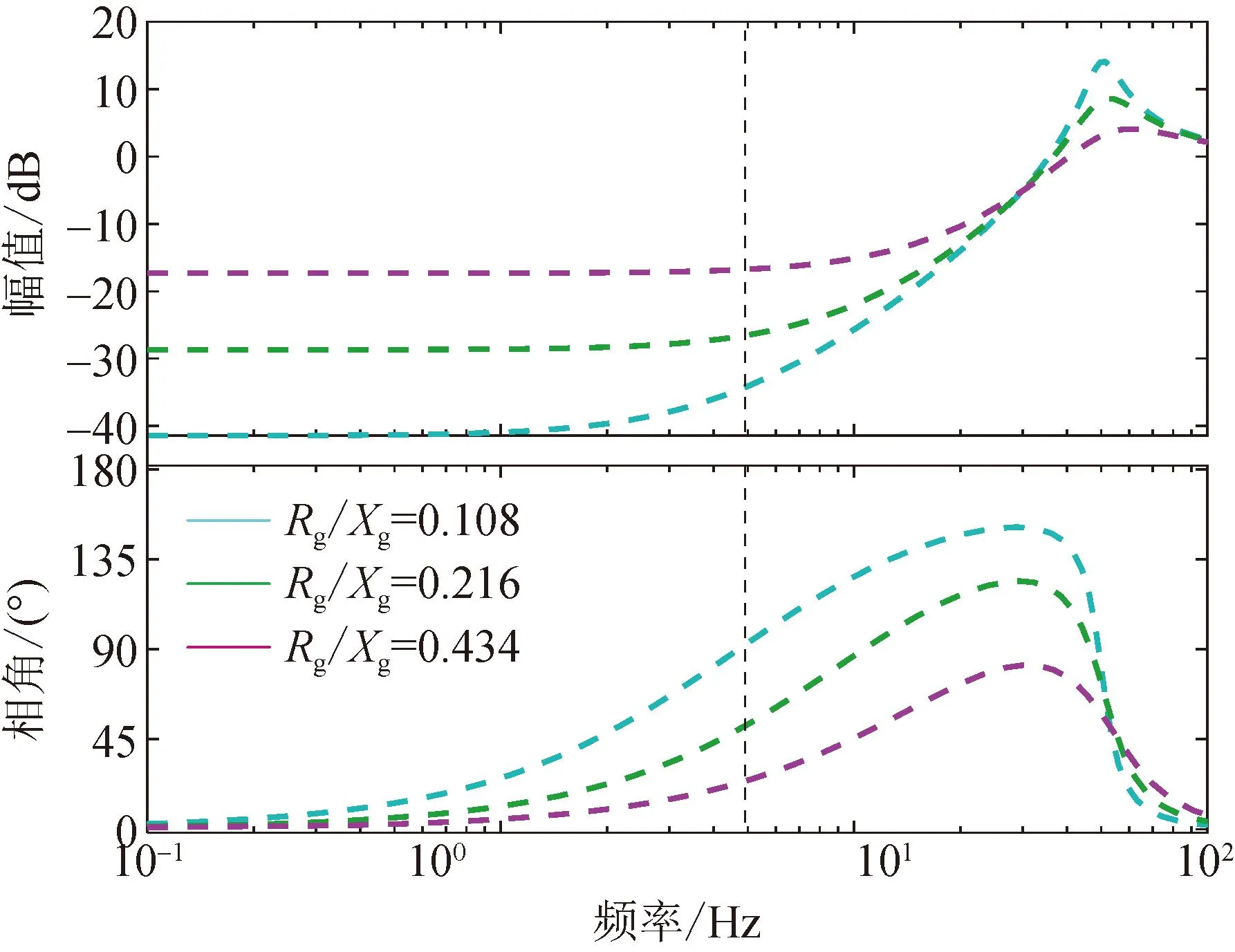
图12 不同Rg/Xg下β12(β21)变化曲线图
3.3 振荡模态λ3,4振荡机理及关键影响因素分析
式(14)有功-功角关系GPδ(s)、无功-电压关系GQE(s)、有功-电压关系GPE(s)及无功-功角关系GQδ(s)都包含了特征方程相同的二阶振荡环节:
(20)
通过式(20)可知,该振荡是由内外环相互作用对应的等效电感Lo与线路电磁暂态共同作用产生的振荡模态,对应38.90 Hz的振荡模态,求解二阶振荡环节,其极点、阻尼比、振荡频率、振荡峰值分别为:
(21)
记线路电感与系统总电感之比λ=Lg/Lg+Lo,则谐振频率ωr=λω0<ω0,谐振频率小于工频。因此当线路呈感性,电阻过小时,振荡模态的实部增大,振荡衰减系数过小,振荡环节对应的极点愈发靠近虚轴,甚至取代低频振荡对应的极点成为主导极点,使VSG并网系统发生38.90 Hz的振荡。当线路呈感性,并且线路电阻越小,为系统提供的阻尼越小,发生该模态振荡的风险越高。
改变内环控制参数,等效改变VSG并网系统的输出阻抗,根据式(21)可知,输出阻抗主要影响系统的振荡频率,输出阻抗越大,振荡频率减小,振荡幅值基本不变,但振荡衰减速度会减小。线路电阻则主要影响次同步振荡幅值,随着线路电阻减小,谐振峰值Mr增大;二阶振荡环节一次项系数减小,对应的阻尼比越小。
引入虚拟复阻抗是抑制VSG并网系统谐振的重点研究策略之一,引入虚拟复阻抗后次同步振荡环节变成了:
(22)
式中:R′=Rg+Rv;L′=Lg+Lv;Rv和Lv分别为虚拟电阻和虚拟电感。虚拟电阻能够通过增加振荡环节的一次项系数2(Rg+Rv)(Lv+Lg)增加阻尼比,削减谐振尖峰、阻尼系统振荡,并且能够使振荡模态特征根左移,降低该振荡发生风险,但同时又会使有功无功耦合加剧。
4 仿真验证
为了验证上文所提的考虑内外环交互作用下VSG并网系统振荡特性理论研究的正确性,在Matlab/Simulink中搭建VSG并网系统进行验证,VSG并网系统具体仿真参数如附录表A1所示。
4.1 不同内环控制参数下系统的响应曲线
图13为不同电压内环比例系数kvp下,t=2 s时有功功率基准从100 kW阶跃到120 kW后VSG并网系统有功功率的输出响应。从图中可以看出,当有功基准值发生扰动时,改变电压内环比例参数时有功输出波形基本保持不变,即电压内环比例参数对系统振荡模态的动态特性不会有太大影响,验证了降阶模型以及阻尼特性分析的正确性。
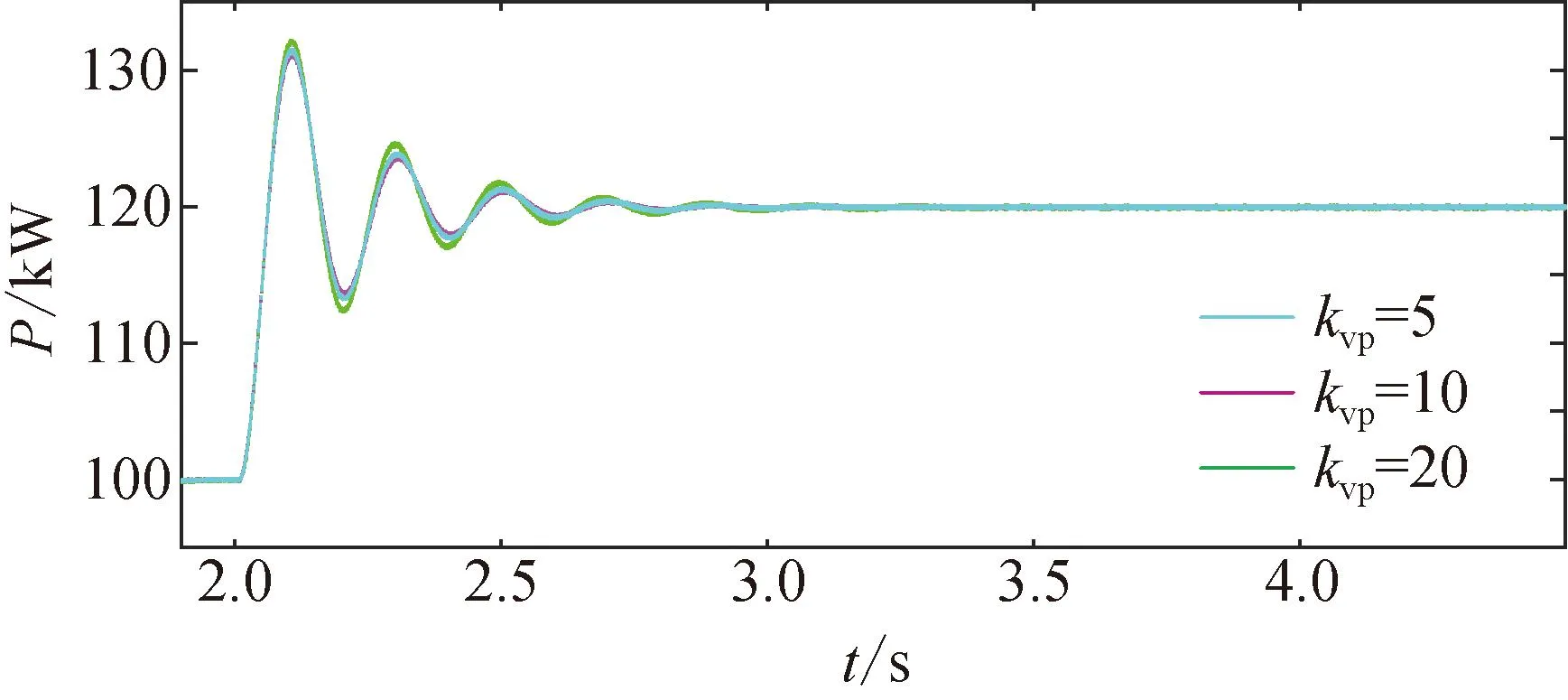
图13 不同比例参数下VSG功率响应波形
图14为不同电压内环积分参数kvi下,有功功率基准值发生阶跃扰动后VSG并网系统有功输出响应波形。从图中可以看出,改变积分参数会对有功输出产生一定的影响,随着积分参数的增大,系统振荡幅值增大,衰减速度减慢,与理论分析随着积分参数的增大负阻尼转矩增大的结果一致。
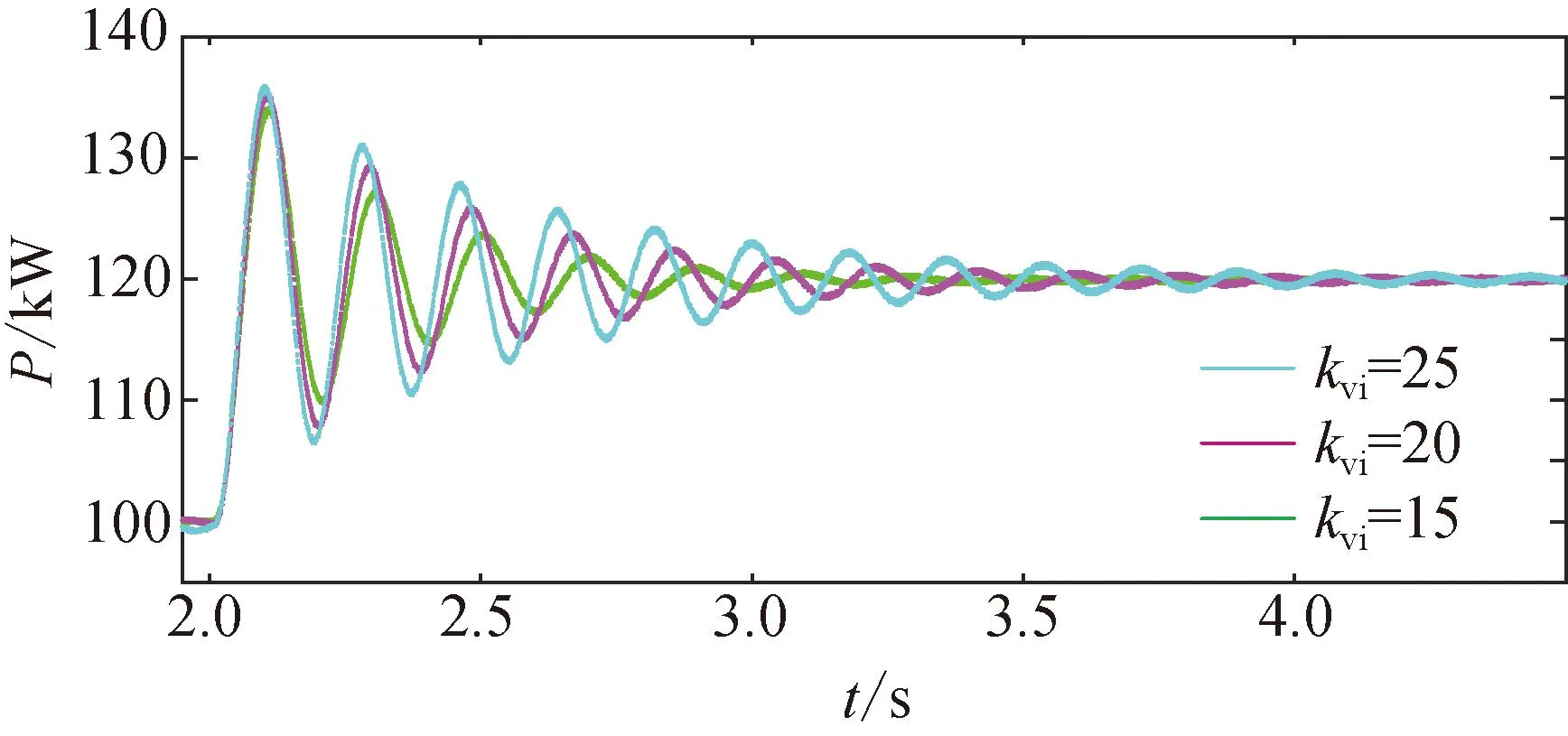
图14 不同积分参数下VSG功率响应波形
4.2 不同线路Rg/Xg下系统的响应曲线
图15为不同线路Rg/Xg下,有功功率基准值发生阶跃扰动后VSG并网系统有功输出响应波形。从图中可以看出,随着Rg/Xg减小(线路电感增大),系统的等效阻尼水平增加,动态过程中功率输出振荡幅值减小。即适当增大线路电感有利于提高VSG的解耦特性,削弱负阻尼效应,提高系统的稳定性。仿真结果验证了理论分析的准确性。
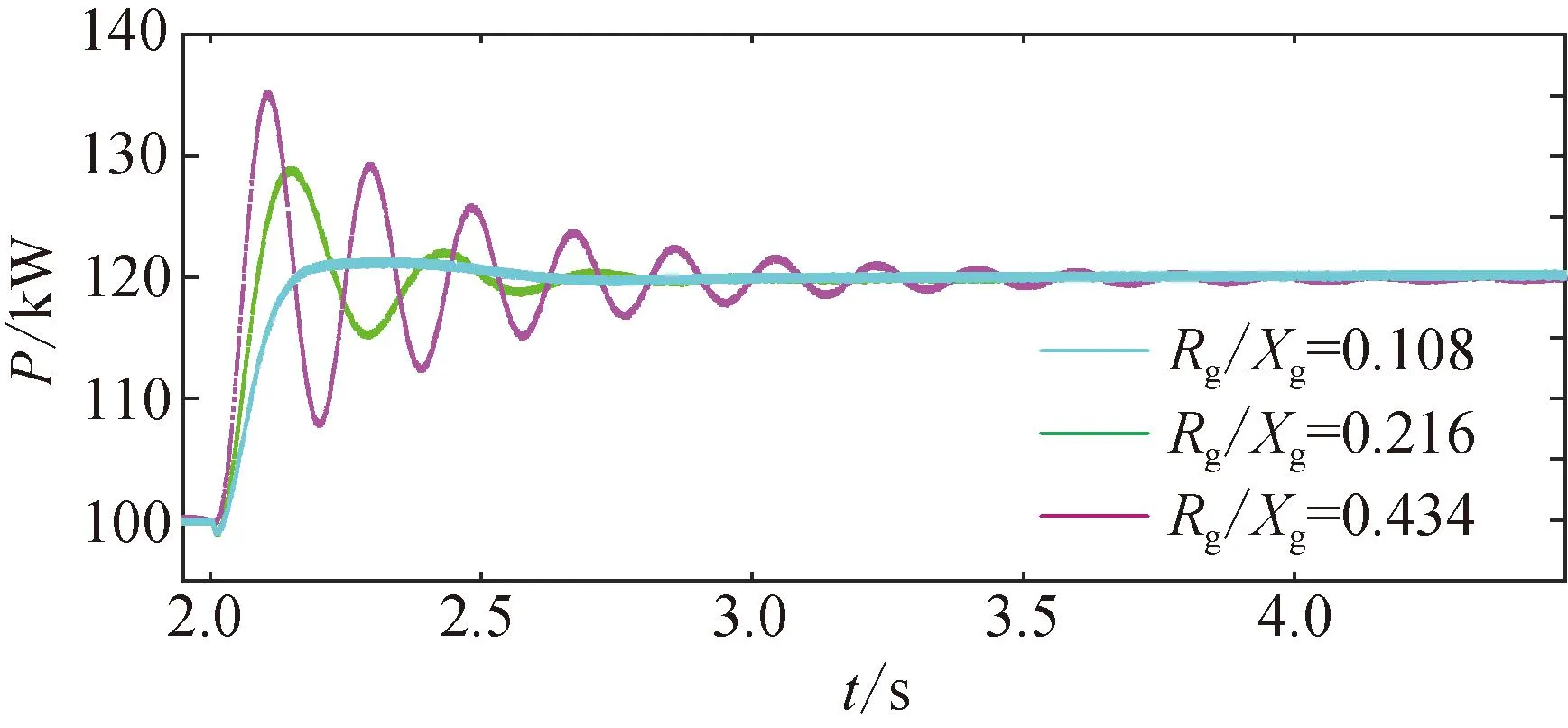
图15 不同线路Rg/Xg下VSG功率响应波形
4.3 振荡模态λ3,4仿真验证
配置参数:阻尼系数kP=50 pu、惯性常数J=0.5 pu,输电线路配置为感性,令线路等效电感Lg=0.1 pu、线路等效电阻Rg=0.01 pu,在2 s时给电网相角2.5°的阶跃扰动,0.1 s后取消,使VSG并网电力系统发生次同步振荡。
图16为VSG并网系统不同输出阻抗以及不同线路阻抗对应的系统功率曲线,从图中可以看出:降低惯量系数、增大阻尼系数并且将输电线路配置为感性时,VSG并网系统发生了次同步振荡,说明此时次同步振荡对应的特征根成为了主导极点。内环控制对应的输出阻抗值增大,次同步振荡频率减小,振荡幅值没有发生变化。
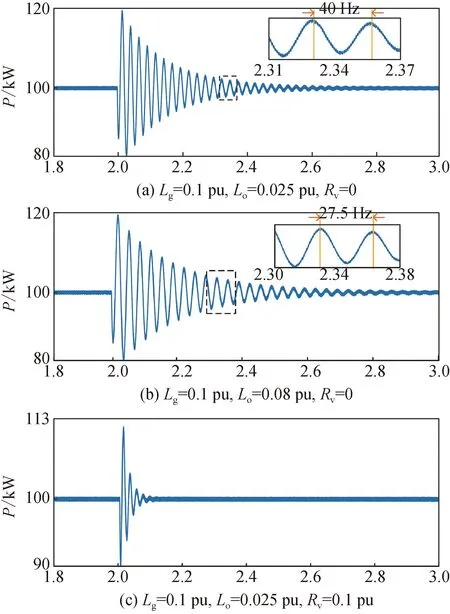
图16 输出阻抗和线路电阻对次同步振荡的影响
通过附加虚拟电阻等效增大线路电阻之后,系统振荡呈衰减特性,并且虚拟电阻越大,衰减越快,系统达到稳定所需时间也越短。仿真结果与理论分析结果一致。
5 结 论
本文选取时间常数作为主导特征建立了考虑内外环交互作用的VSG并网系统降阶模型,研究了VSG控制引入的两种振荡模态。相关结论如下:
1)虚拟同步控制内外环交互作用表现为逆变器等效输出阻抗的形式,输出阻抗大小主要与电压内环积分系数有关。
2)改变电压内环比例参数对系统的主导振荡模态影响不大,系数增大会使系统该振荡模态的负阻尼转矩略微增大,稳定裕度减小,系统振荡幅值增大。
3)在一定范围内增大线路电感,随着线路Rg/Xg减小,有功无功功率之间的耦合得到改善,主导振荡模态的负阻尼转矩减小,系统稳定性增强。当线路呈感性并且线路电阻较小时,线路阻抗与输出阻抗共同作用产生的振荡模态可能成为主导振荡模态,振荡风险变大,系统稳定性变差。
本文研究了工频带宽范围内系统的动态特性,辨识了影响系统次同步振荡的关键影响因素以及振荡机理。在后续研究中,将进一步扩展所研究的带宽范围,并提出相应的振荡抑制策略。
