考虑全生命周期碳排放的电氢耦合VPP调度优化

2024-04-02闫庆友党嘉璐林宏宇郑浩伟

电力建设 2024年4期

闫庆友,党嘉璐,林宏宇,郑浩伟

(1.华北电力大学经济与管理学院,北京市 102206;2.国网经济技术研究院有限公司,北京市102209)

0 引言

当前国内正处于实现“双碳”目标的转型关键期,全球能源市场受经济、政治等多种因素影响仍处于动荡调整过程中,绿色低碳能源的利用发展将成为重构全球能源市场的重要驱动力[1-2]。复杂的国内外部环境致使我国能源电力系统低碳转型压力日益增大。为此在统筹兼顾能源市场用户、各类电力生产与运营主体利益平衡的基础上,构建国内新能源完整产业体系并超前规划布局关键技术势在必行[3]。比如,与可再生能源结合利用的储能、氢能,与分布式资源结合的虚拟电厂(virtual power plant,VPP)等。充分挖掘VPP在生产、建设、运输以及回收等多环节的低碳潜能,是促进可再生能源消纳,提高低碳调度决策水平的重要手段[4]。

在新能源大规模并网后,如何将分布式电源、常规可控机组、用户灵活负荷和储能装置等聚合成可控整体VPP,成为目前新型电力系统调度领域的一个重要研究方向。在风光火联合调度系统中,电化学储能的引入可以平抑高比例新能源发电波动[5-7]。但电储能技术充放类型单一,风光消纳受限,难以实现规模化经济性能源存储。电转气设备可以通过多能互补达到能源综合高效利用,实现电力网络和天然气网络之间的双向能量流动[8]。文献[9-10]以运行成本、经济效益作为目标函数,提出了虚拟电厂电-热-气协调随机优化调度模型。文献[11]以混氢天然气置换传统天然气气源,提出一种降低系统对外部气网依赖度的低碳经济调度策略。文献[12]提出了一种基于固体可逆燃料电池的新型电-掺氢天然气优化调度模型。上述文献多聚集于电转天然气或掺氢天然气的耦合互补利用,对单独的电转氢气参与电力系统应用场景的研究较少,电转气实际是在电转氢的基础上,再将氢气甲烷化,电转天然气的效率约为49%～65%,而电转氢气的效率约为51%～77%,后者具有更高的转化效率和工业泛用性[13],还有很大的研究空间。

如何确定系统构成单元的运行约束并选择合理的优化目标是VPP优化调度的关键,国内外诸多学者从电碳结合的视角出发,针对VPP低碳经济调度展开研究。文献[14]在多时间尺度上提出了考虑多主体运行阶段碳中和成本的VPP双层协同优化调度模型。文献[15]分析了碳价型敏感负荷对需求响应的影响。但上述文献引入的碳视角过于简单,未充分考虑碳交易市场的引导作用。碳交易是减少碳排放量的有效措施之一,主要分为传统碳交易机制和阶梯式碳交易机制。文献[16-17]在含电动汽车的虚拟电厂经济目标函数中引入传统碳交易成本。文献[18]将阶梯式碳交易引入风光储联合系统的分布鲁棒优化调度中。文献[19]考虑季节要素对碳交易的影响,提出了基于奖惩阶梯碳价的季节性碳交易机制。文献[20]在电-气-热综合能源系统中引入阶梯式碳交易。综上,通过与传统碳交易对比得出阶梯式碳交易对碳排放量有更为严格的控制,有效约束了系统运行的经济和环境成本。以上研究虽然都是从碳视角出发,但并未对低碳调度中能源的生产、传输、储存等行为进行全过程碳轨迹追溯。因此亟需更精确地测量系统构成单元所有环节的碳排放量,拓宽VPP各设备碳排放计量模型的应用范围,进一步提高VPP低碳调度的准确性。

综上所述,本文将分布式储能、电转氢系统与常规虚拟电厂进行集成,并运用生命周期评价(life cycle assessment,LCA)方法分析各类能源设备主体各环节产生的碳排放,进而精确计量碳排放系数,并将其与阶梯碳交易机制联合纳入约束条件中,以系统总运行成本最小,碳排放量最少为目标建立电氢耦合虚拟电厂多目标调度优化模型,最后通过算例分析验证所提模型的有效性和可行性。

1 虚拟电厂结构

1.1 基本结构

本文在拥有电、氢两种负荷的虚拟电厂中引入分布式电储能,包括独立的电池储能系统、储能与分布式电源相结合(如光储、风储系统),并将储能设备与微型燃气轮机(gas turbines,GT)、风电机组(wind turbine,WT)、光伏阵列(photovoltaic,PV)及氢燃料电池汽车群等组件集成电氢耦合虚拟电厂。设定可中断负荷参与虚拟电厂的优化运营,在电力用户侧实施激励型需求响应[21]引导用户用电行为。分布式储能既能充当电源又能作为负荷,可根据系统实时运行需要调节其充放电功率,在夜间负荷较低而风电高发时期或夏季负荷较高而光电高发时期,将过剩的风电和光电转化存储到分布式蓄电池中。多余的风光发电量可通过电转氢技术[22]生成氢气供氢燃料电池汽车(hydrogen fuel cell vehicle,HFCV)充氢使用,提供现阶段高价氢气下的另一种成本疏导机制。VPP基本结构如图1所示。

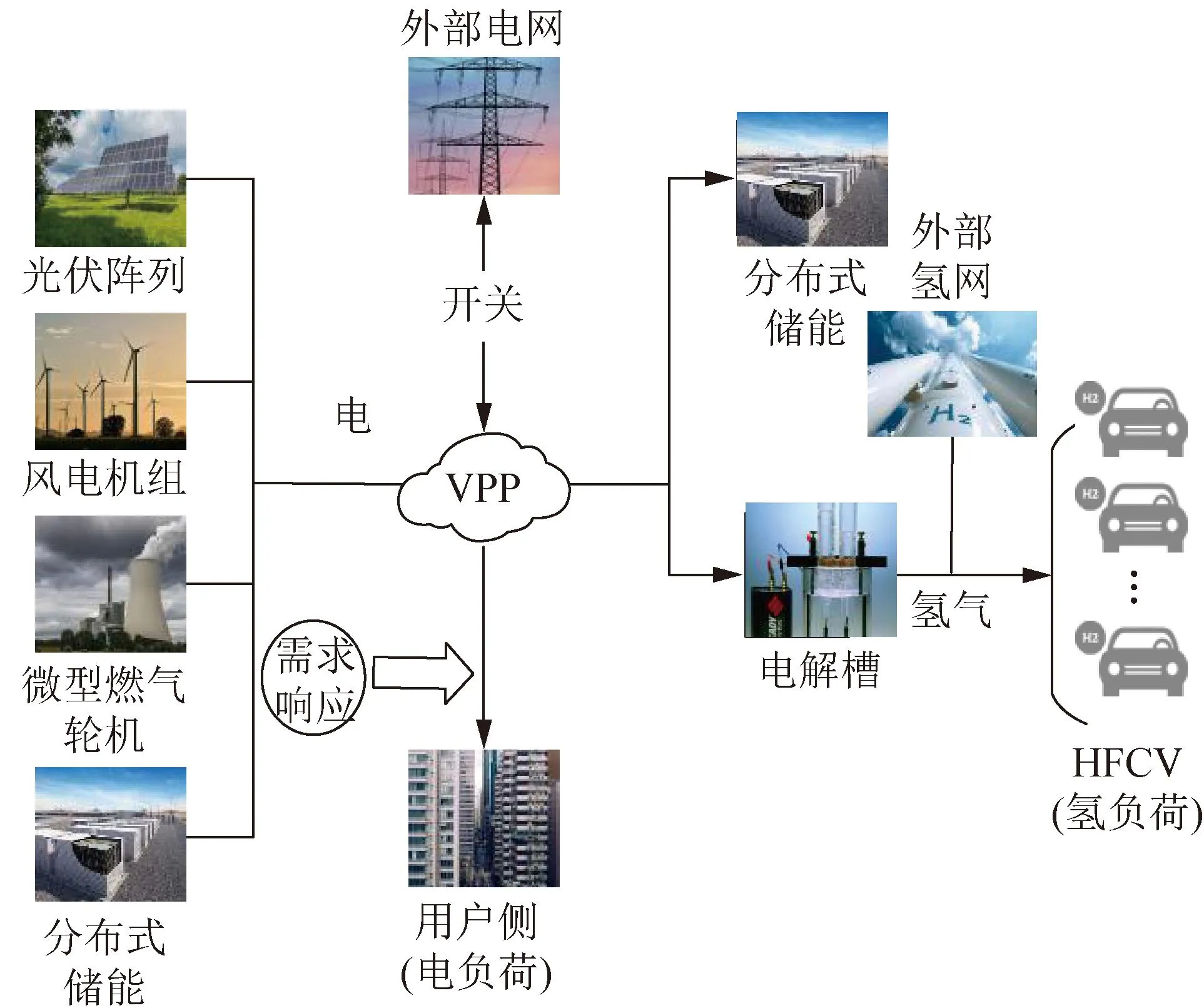
图1 虚拟电厂基本结构

1.2 VPP典型设备模型

1)风电模型。

风力发电通常情况下服从威布尔分布,在不同的风速下,风力涡轮机的输出功率Pwt是不同的。两者之间的关系表示如下:

(1)

式中:a、b、c、d为风力涡轮机的出力系数;vi、vr、v0分别为风力涡轮机的切入速度、切出速度和额定速度;pr为额定功率。

2)光伏模型。

影响光伏发电输出的因素是光伏面板温度、太阳辐射强度和环境温度。光伏系统的输出功率Ppv为:

Ppv=SPVGPVβPV[1+k1(Tc-Tr)]

(2)

式中:SPV表示环境温度;GPV为太阳辐射强度;βPV表示太阳能转化效率;k1为组件的温度系数;Tc、Tr分别为光伏面板温度和参考温度。

3)微型燃气轮机模型。

燃气轮机可以将天然气的热能转化为电能,在系统优化中输出功率为Pgt,研究体系已经较为成熟。燃气轮机的运行模型如下:

Pgt=QTCSHTCS·ηTCS

(3)

式中:ηTCS为燃气轮机的运行效率;QTCS为天然气消耗量;HTCS为天然气热值。

4)柔性负荷需求响应模型。

基于事先签订的需求响应合同,由VPP运营商向柔性负荷用户直接发出负荷削减的控制信号,改变用户用电量,则用户参与调度后的负荷功率Pue为:

Pue=(1-θudγud)Puo

(4)

式中:γud为0-1变量,表示用户负荷的削减状态;θud为负荷削减系数,θud∈[0,1];Puo为削减前的原始用户负荷功率。

1.3 分布式储能模型

分布式储能接入电网后既能充当分布式电源又能等效为用电负荷,作为新能源与电网之间的缓冲设备,能够有效地保证电网的稳定灵活运行。根据储能与电网双向功率交换的流向,分布式储能运行状态可分为三种:充电、空闲、放电[23]。储能出力Psoc表示如下:

(5)

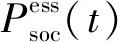
当分布式储能从电网中吸收电能时,即充当用电负荷时,对应的充电模型如下:

(6)

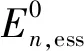
当分布式储能向电网中释放电能时,即充当分布式电源时,对应的放电模型如下:

(7)

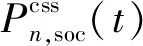
当分布式储能与电网之间无电能流动,即处于空闲状态时,对应的模型如下:

En,ess(t)=En,ess(t-1)

(8)

1.4 电转氢系统模型

1)电解槽模型。

在风光资源充足条件下,质子交换膜(proton exchange membrane, PEM)电解槽(electrolysis bath,EL)[24]利用多余电能电解水制氢,为氢燃料电池汽车充氢。电解槽能够将水电解为氢气和氧气。其数学模型为:

(9)

(10)

2)氢燃料电池汽车模型。

假设HFCV并网时段内保持额定功率充氢,不可调度,直至满足续航里程需求后离网,选取行驶里程作为测量HFCV已充氢量的指标[25],HFCV集群模型如下:

(11)

(12)

(13)

(14)

2 虚拟电厂低碳经济优化模型

2.1 基于多主体全生命周期的碳排放系数计量

VPP的总碳排放量包括各主体直接或间接产生的碳排放,其中涉及多种能源相互耦合,不同能源设备在生产投运过程中直接或间接向大气中排放CO2的强度即为该主体的碳排放因子[26]。风电、光伏被普遍认作清洁能源,在运行阶段未直接排放CO2,此阶段碳排放强度为0,但其在生产、运输、运维、报废回收等环节还是会导致碳排放,因此在分析VPP碳排放时,需要结合LCA能源链碳排放分析法[27],将各类能源设备主体的能源流动过程进行简化,然后根据各个环节内能源消耗或转换过程所产生的碳排放系数进行计量,发电侧主要计量来源为气电、新能源发电和电制氢,用电侧主要来自储能,能源在输配过程中的碳排放损耗暂不考虑,各类机组的单位电量全生命周期碳排放系数计量为:

(15)

式中:epg,i为机组i生产环节的碳排放系数;cjg为单位标准电量与能耗的折算系数;mct,i、mpj,i为机组i生产环节和施工过程材料使用的碳排放强度;ect,i、epj,i为机组i生产环节和施工过程材料耗费能量强度;etg,i为机组i运输环节的碳排放系数;my,i为机组i第y种组件的碳排放强度;ey,i为机组i第y种组件运输耗费能量强度。

1)化石能源机组(煤电、气电)。

煤电LCA的碳排放主要来自煤炭生产、电煤运输、燃烧3个环节。煤制天然气和油田天然气的生产开采、运输和燃气发电3个环节的碳排放为气电的LCA碳排放主要组成部分。

(16)

式中:Epgs为生产环节碳排放系数,此时i分别为燃煤和燃气机组GT;Up为生产过程的单位能耗;Uep为煤炭的生产排放系数;λep为单位电量生产损失率;Etgs为运输环节碳排放系数;Eggs为发电环节碳排放系数;Usg为单位电量的供电标准气耗;Utce为单位发电的碳排放当量系数。

2)新能源机组(风、光、电解槽)。

新能源机组的生产建设和出厂运输两个环节是LCA碳排放主要来源,而运维环节的碳排放主要来自耗材生产与替换时运输耗能和设备检修耗能,但此部分的碳排放量相较LCA的碳排放量极少,通常忽略不计。假设电解水制氢过程中电力消耗隐含的碳排放已并入VPP机组发电碳排放。

(17)

式中:Epeg为新能源机组生产环节的碳排放系数,i分别取风电、光伏、电解槽;Eteg为新能源机组组件运输环节的碳排放系数。

3)储能机组。

储能机组在使用和废弃回收阶段会产生较多的碳排放,故对于VPP在计量总碳排放量时,此部分碳排放也应包含在内。因此,将储能设备全生命周期边界确定为计及生产、建设、运输以及回收的过程,即

(18)

式中:Epsg为储能机组在生产环节的碳排放系数;Etsg为储能机组在运输环节的碳排放系数;Eosg为储能机组在运行环节的碳排放系数;mso为日充放电次数;nso为运行环节的替换系数;Ersg为储能机组在废弃回收环节的碳排放系数;cgi为电池电量与电池能耗之间的折算系数;rgi为电池材料组件运往废弃回收工厂单位距离消耗能源的碳排放强度;lgi为电池材料组件运往工厂的运输距离。

4)外部市场。

外部市场购电和购氢的碳排放量均取决于当地电网的发电能源构成,本文参考北方某地的构成比例,其中煤电约占50.3%,天然气发电约占30.7%,光伏和风力发电分别占比约为7.8%和11.2%,结合各主体全生命周期碳排放系数加权计算可得购电的LCA碳排放系数。现阶段氢网市场主要制氢方式仍为化石能源制氢,煤制氢约占63.5%,天然气制氢约占36.5%,其他含有电力消耗带来隐含碳排放的制氢方式暂不考虑。

2.2 阶梯式碳交易成本模型

碳交易[28]是允许生产商在市场中进行合法的碳排放权买卖进而达到控制碳排放目的的一种交易机制。由政府监管部门向各碳排放源分配碳排放配额,若实际碳排放高于所分配的配额,则需要购买碳排放权超额部分,反之多余的配额可以在碳交易市场中出售。阶梯式碳交易成本模型[29]主要包括碳排放权配额模型、实际碳排放模型、阶梯式碳排放交易模型。

1)碳排放权配额模型。

VPP中的碳排放源主要有4类:燃气轮机、新能源机组、上级购电和购氢。本文主要采用的配额方法为无偿配额。

(19)

2)实际碳排放模型。

基于各类机组的单位电量全生命周期碳排放系数计量的碳排放量:

(20)

3)阶梯式碳交易成本模型。

相较于传统碳交易定价机制,为进一步控制碳排放,本文采用阶梯式定价机制,需要购买的碳排放权配额越多,相应区间的购价越高,基于该机制建立的阶梯式碳交易成本模型如下:

(21)

(22)

2.3 目标函数

如何合理分配系统内部运行收益并提高上网购售收益是VPP首要优化运行的目标,由于电解水制氢具备低碳特性,更多碳配额可以进入市场交易,因此碳排放量最小化作为本文第二个优化目标。通过使系统运行总成本F1和总碳排放量F2最小,实现电氢耦合VPP在经济效益和环境效益方面的最优化,目标函数如下:

(23)

式中:F1为燃气轮机、风电、光伏及分布式储能系统和电转氢系统参与优化调度的电网运行成本;C1为主设备投资成本;C2为用户可削减负荷的补偿成本;C3为阶梯式碳交易成本;C4为电网购售电成本;C5为电转氢系统购氢成本。

主设备投资成本包括初始购买费用、辅助设备投资费用、总替换费用和总运维费用,辅助投资费用与初始购买费用成正比例关系,运维费用包括燃料费用和设备维护费用。在虚拟电厂寿命周期内,只考虑蓄电池和电解槽的重置成本,蓄电池和电解槽的寿命周期分别为5年和10年。因此,主设备投资成本可表示为:

C1=Ccap+Crop+Crep+CGT

(24)

Ccap=cgt+cwt+cpv+csoc+cel

(25)

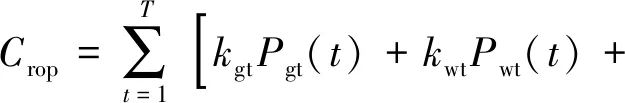
(26)

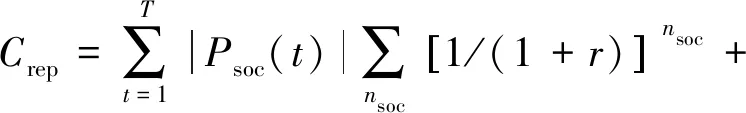
(27)

(28)

式中:Ccap为初始购买费用,包括燃气轮机、风光机组、蓄电池、电解槽等设备;Crop为分布式电源的运行成本;Crep为总替换费用;CGT为燃气轮机的燃料成本;cgt、cwt、cpv、csoc、cel分别表示燃气轮机、风电机组、光伏机组、蓄电池、电解槽的购买价格;kgt、kwt、kpv、ksoc分别为燃气轮机、风电、光伏机组、蓄电池的运行成本系数;r表示行业基准收益率,设定r=8%;nsoc、nel分别表示蓄电池和电解槽的运行寿命;kGT为燃料成本系数。

用户可削减负荷[30]的补偿成本为:

(29)

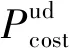
阶梯式碳交易成本为:

(30)

虚拟电厂向电网购售电成本为购电费用减去售电收益,公式如下:

(31)

HFCV集群可从电转氢系统完成充氢需求,减少从外部市场购买氢气,电转氢系统的购氢成本计算如下:

(32)

式中:cp,h为市场上每单位体积氢气价格。

2.4 约束条件

风电、光伏、气电与储能联合运行时要综合考虑自身与电网的运行约束[31],模型需满足的约束条件如下:

1)系统功率平衡约束:

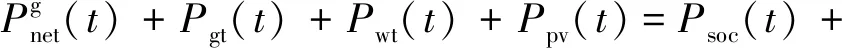
(33)

(34)

式中:PD(t)为用户电负荷;Vnet为向氢网购氢量。

2)功率上下限约束:

(35)

(36)

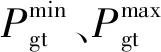
3)主网约束:

(37)

(38)

4)蓄电池约束:

(39)

Esoc(0)=Esoc(24)

(40)

(41)

5)可削减负荷约束:

0≤Pue≤εmaxPuo

(42)

式中:εmax为最大负荷削减率。

6)电转氢系统约束见式(10)和(14)。

2.5 多目标模型求解

本文建立的虚拟电厂调度优化模型有2个目标函数,分别以经济成本最低,碳排放量最低为目标函数求解模型,并在各目标函数最优条件下求解其他函数,用二维表格表征目标函数之间的相互关系。并根据各目标函数的最大值和最小值确定权重系数,将多目标函数加权转化为单目标函数便于进一步的求解。由于目标函数中,系统运行成本属于经济成本型目标函数,二氧化碳排放量属于社会成本型目标函数,不同目标函数量纲也不相同,需要进行无量纲化处理:

(43)

式中:Fij为在Fj(j=1,2)最优条件下Fi(i=1,2)的取值;通过对Fij处理后,可以得到无量纲化目标函数F′ij。

应用熵权法为各目标函数赋予权重,详细赋权步骤见文献[32]。最后,将多目标函数通过加权得到单目标函数F进行求解:

(44)

式中:fi为目标函数F′i的权重系数。

3 算例分析

3.1 参数设置

为验证本文所提低碳经济优化调度模型的合理性和可行性,本文以华北某园区[33]为算例进行仿真分析,按时间分别选取夏季、过渡季、冬季3个典型场景。以10 MW的风电机组,6 MW的光伏机组,3 MW的燃气机组,2 MW的电转氢设备集成虚拟电厂,另外,虚拟电厂内还有总额定容量为2 MW·h的分布式储能设备和最大削减率εmax=10%的可削减电负荷,氢负荷为1 000辆氢燃料电池汽车。VPP各机组的详细参数见表1,电转氢系统的详细参数见表2,HFCV的计算参数见表3,主网分时电价见表4,不同季节典型日的风光出力曲线见图2。

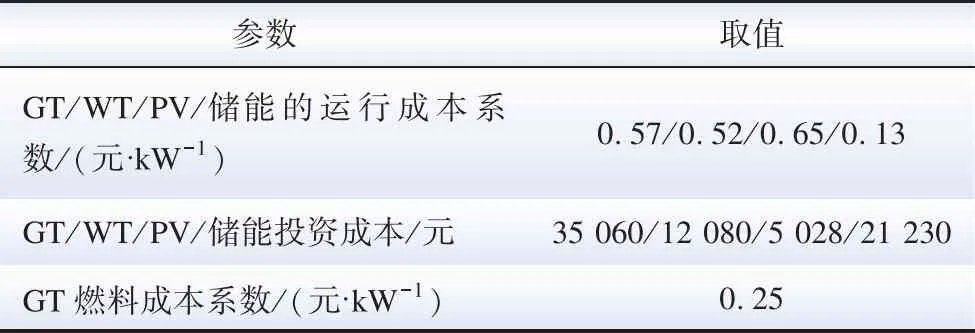
表1 系统出力及储能相关运行参数

表2 电转氢系统相关运行参数

表3 氢燃料汽车相关参数

表4 电网分时电价

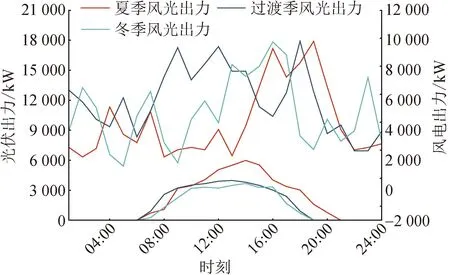
图2 不同季节典型日风光出力曲线

VPP与主网购售电价按照峰平谷三段划分,峰时段为11:00—16:00,19:00—22:00;平时段为08:00—11:00,16:00—18:00及22:00—24:00;谷时段为00:00—08:00。

根据第2节多主体LCA碳排放计量方法,计算得到各类能源设备在各环节的碳排放系数如表5所示,区域电网购电的碳排放系数为803 g/kWh,根据参考文献[34],氢网加氢的碳排放系数约为60.79 g/m3,碳交易基价λ=25元/t,区间长度l=2 t,价格增长率α=25%。参考北京市发改委、广东省生态环境厅等出台的有关政策,各能源设备碳排放配额如表6所示。

表5 VPP各设备在各环节的碳排放系数

表6 单位碳配额系数

在仿真分析中,本文构建的考虑全生命周期碳排放的电氢耦合VPP低碳经济调度模型为混合整数线性规划模型,采用Matlab R2021a软件,通过Yalmip工具包调用CPLEX求解器对算例进行求解。

3.2 情景设置

为了充分说明本文所构建考虑全生命周期碳排放的电氢耦合VPP多目标优化模型的可行性,本文首先以过渡季典型日场景为算例,从各目标函数最优角度设置3个情景。情景设置如下:情景1以系统运行成本最低为优化目标;情景2以碳排放量最低为优化目标;情景3以多目标作为优化目标。由于风光出力易受季节特性的影响发生波动,且夏季和冬季的用户负荷需求要大于过渡季,因此从不同季节典型日的角度增加2个算例,进一步验证文章模型的有效性。

3.3 算例结果

以经济成本最小为目标函数时,碳排放量较高,缺乏环保性;以碳排放量最低为目标函数时,经济效益较低,牺牲了一部分经济效益;所以,情景3中综合考虑多个目标实现VPP的最优运行,求解单目标函数的二维关系表,f1、f2权重系数计算结果为0.66和0.34。过渡季典型日整体优化结果如表7所示,夏季和冬季典型日整体优化结果见附录A,风光出力、电解槽功率和三种情景下燃气轮机出力如图3所示。

表7 过渡季整体优化结果

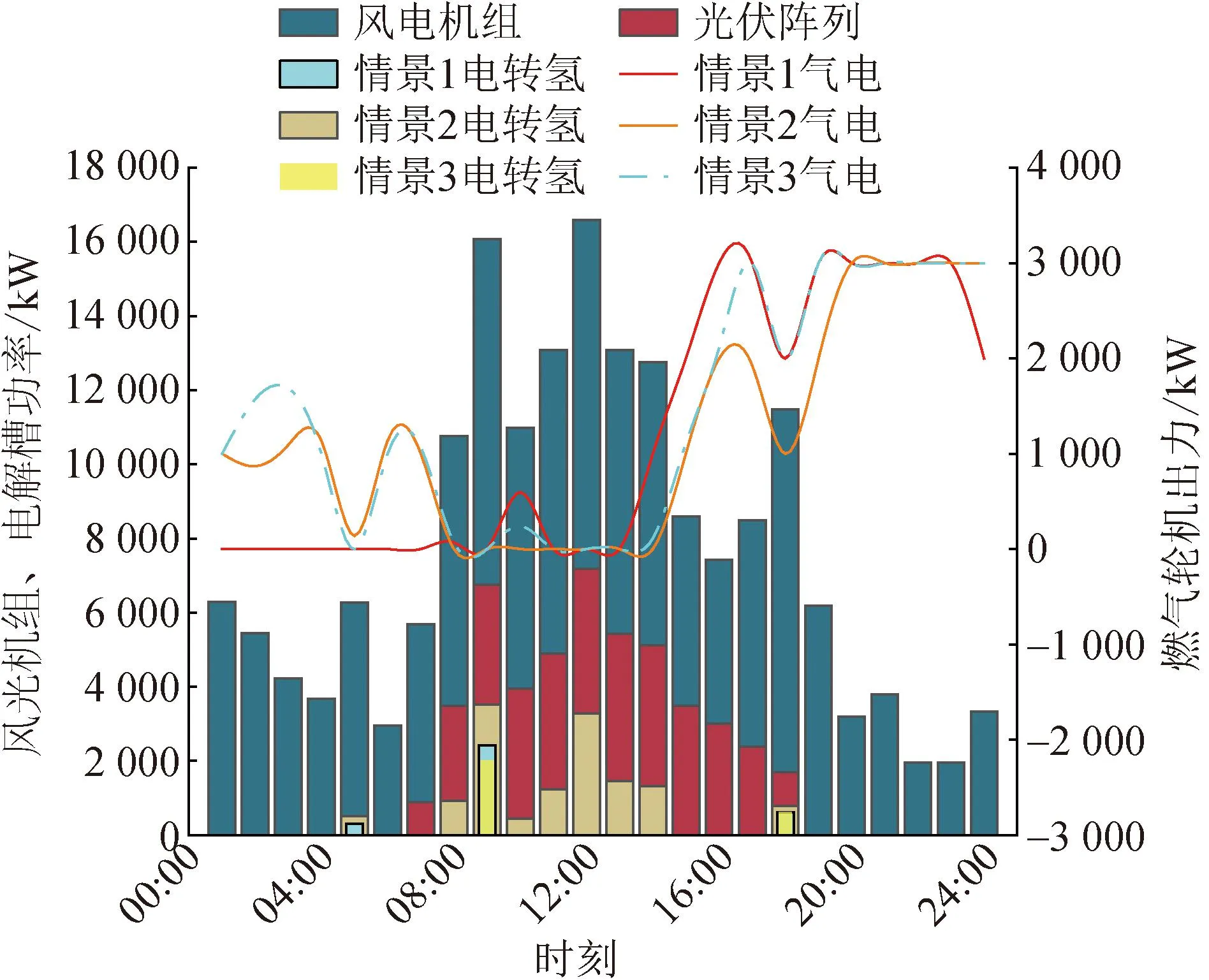
图3 VPP过渡季出力优化结果

由表7和图3中发电机组出力数据分析可得,情景1以最小运行成本为优化目标,寻求VPP经济最优的调度策略,此时GT发电量为28.66 MW·h,前期出力较少,15:00之后光伏出力越来越小,GT出力增多,该情景下,VPP成本相对最低,运行经济效益较为乐观,但系统低碳性欠缺考虑。情景2以最低碳排放量为目标函数,达到环境效益最佳,相对情景1,GT出力明显增多且达到29.30 MW·h,01:00—07:00时GT也开始出力,VPP碳排放量减少了8 364.54 kg,但运行成本增加了10 424.02元,此情景下VPP碳排放得到有效降低但经济效益不佳。情景3将多个目标作为优化对象,在确保VPP经济效益前提下,减少碳排放,此时GT发电量为33.97 MW·h,VPP碳排放量对比情景1减少了6 441.49 kg,总运行成本对比情景2减少了8 023.33元,此调度方案兼顾了经济效益和环境效益。

3.4 不同优化目标对比分析

3.4.1 考虑电转氢机制效益分析

各情景下的VPP购售电和购买氢气结果对比如图4所示,正值表示VPP从主网购电购氢,负值表示VPP向主网售电。

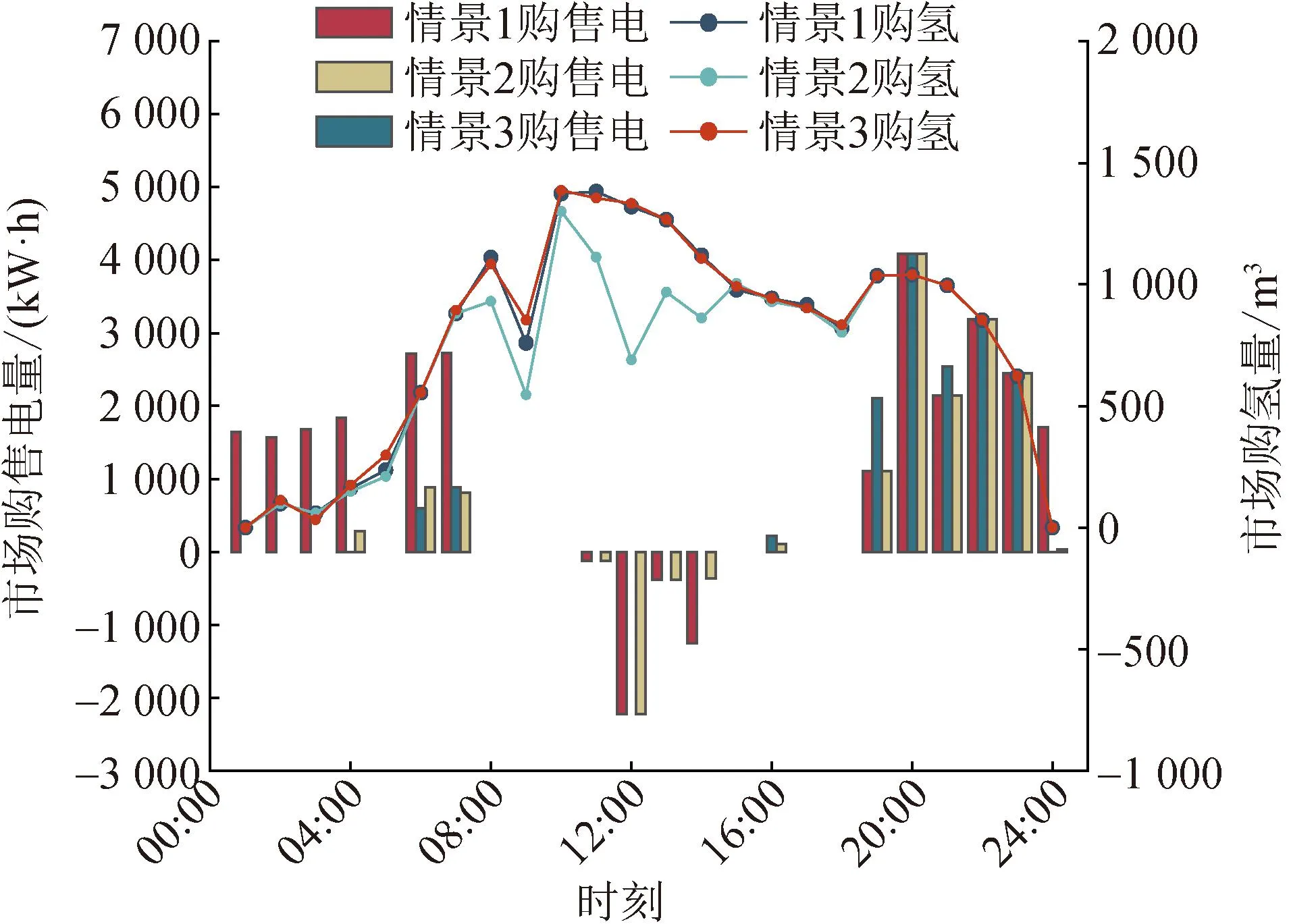
图4 VPP过渡季和主网(电氢)交换结果

结合图4和图3中电转氢功率分析可得,在情景1条件下,VPP主要在午间峰时段向电网和用户共出售电能3.97 MW·h,在平时段、谷时段和19:00—21:00从电网购电29.55 MW·h, 电解槽出力3.36 MW·h,总购氢18 524.3 m3。情景2下VPP不再售电,购电减少了13.47 MW·h,电解槽出力大幅增加至13.46 MW·h,这是由于主网发电构成复杂,碳排放量更高,VPP更多采用GT进行削峰填谷,多余的电量进行电转氢气,使得购氢量减少了1 979.7 m3。情景3中VPP购售电量均介于情景1、2之间,分别为18.29 MW·h和3.08 MW·h,但购氢量相对于情景1增加142.13 m3,电解槽出力降低到2.64 MW·h,VPP主要在平、谷时段购电,此时购电成本小,在午间峰时段售电,此时售电价格高,在风光出力充足时进行电转氢,更充分地消纳风光出力,减少从外部市场购买高价氢气,提高经济效益。

3.4.2 考虑储能系统效益分析

储能系统蓄电量及充、放电功率如图5所示。

图5 VPP过渡季储能优化结果

结合图5和图3中光伏出力数据分析可得,光伏机组在07:00才开始发电,因此在峰时段11:00到来前,不同情景下储能系统最多只有3 h进行充电操作,又由于电储能成本相对较高,结合图3中GT出力数据分析可得,情景1在追求最低经济成本时,GT出力最小,更倾向于从主网购电购氢,储能系统充电时长仅为5 h,充电效率最低。结合图4主网交换数据进一步分析可得,情景2中GT出力增加,受主网购电购氢碳排放系数较大的影响,更倾向于内部发电出力,储能系统在平、谷时段充电时长增多,更早地达到了最大蓄电量。在以多个目标为优化对象的情景3中全天平均蓄电率为33.37%,高于情景2的30.05%和情景1的32.25%,此优化方案提高了储能单元的利用率,更充分地利用峰谷价差进行“低储高放”、“谷购峰售”,既能保证VPP较高收益,又能减少碳排放。

3.4.3 考虑阶梯式碳交易机制效益分析

为了有效地验证阶梯式碳交易政策对VPP低碳经济调度的影响,采用所提模型和传统经济调度模型(即系统运行成本中不考虑碳排放成本)对过渡季典型日算例补充设置3个情景进行对比:情景4为传统碳交易机制下采用传统经济调度模型;情景5为阶梯式碳交易机制下采用传统经济调度模型;情景6为阶梯式碳交易机制下采用所提多目标模型,表8为3种运行情景下的调度结果。

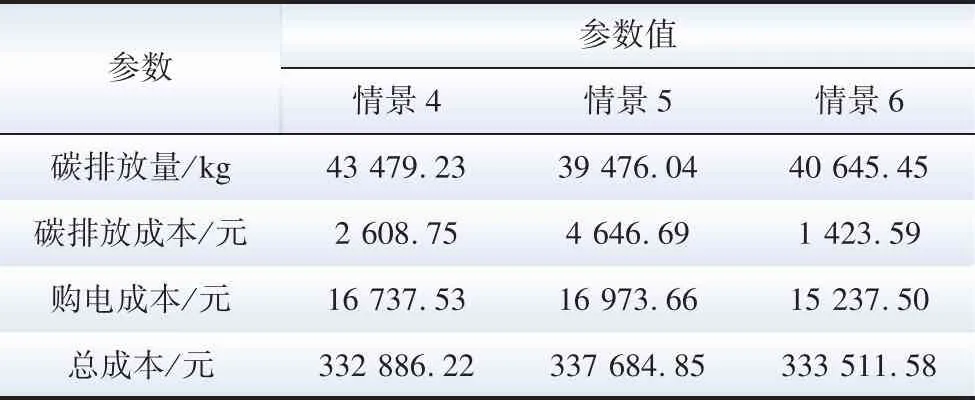
表8 VPP阶梯式碳交易机制前后结果对比

由表8可知,情景5碳排放量比情景4减少了9.21%,情景6碳排放量比情景4减少了6.52%,可见考虑阶梯式碳交易机制能进一步约束碳排放,达到清洁低碳的目的。虽然情景6较情景5的碳排放量增加了1 169.41 kg,但总成本减少了4 173.27元,体现了本文所提多目标优化模型能同时兼顾经济利益和环境效益。对比3种情景的总成本,情景5的碳排放量虽然略低于情景6,但由于优化时未考虑碳交易成本,VPP需要向碳交易市场购买大量的碳排放权配额,因此总成本最大;情景4相比情景5虽然增加了购电成本和碳排放量,但由于碳交易机制为传统的恒定价格机制,因此碳交易成本较低,总成本最小;结合表5的各主体碳排放系数可知,燃气轮机的单位碳排放量要小于主网购电的单位碳排放量,由于阶梯式碳交易机制的原因,情景6减少购电,增加气电出力,达到新的平衡。

3.5 不同季节典型日的对比分析

本文基于情景4、5继续对夏季和冬季典型日场景下VPP各单元出力及负荷进行分析,证明所提出模型面对不同季节的不同系统供电组成和负荷配置都有效。不同季节VPP购售电和购买氢气结果对比如图6所示,图7和图8分别展示了夏冬季典型日的VPP出力情况和电、氢负荷数据,夏季和冬季典型日整体优化结果如表9所示。

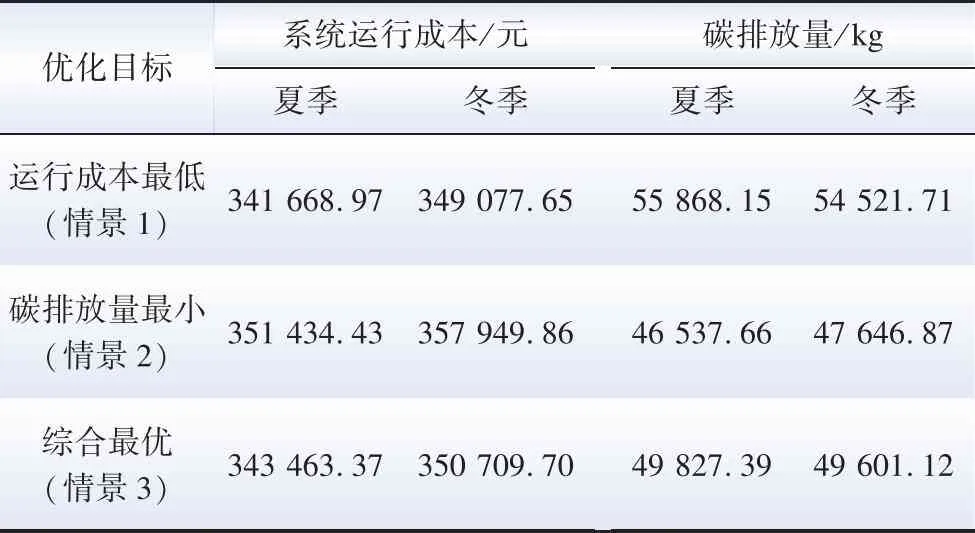
表9 夏冬两季整体优化结果

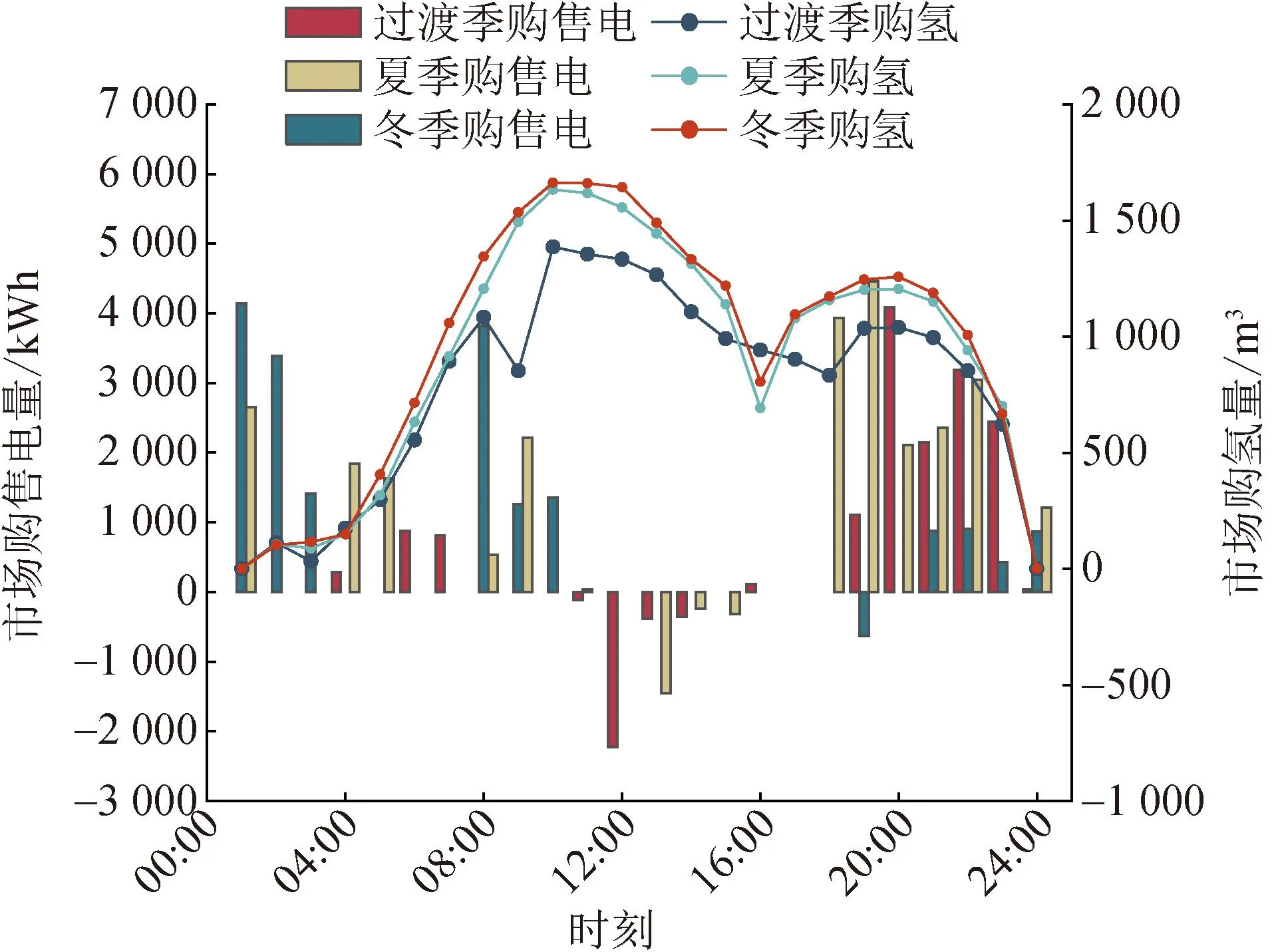
图6 VPP不同季节和主网(电氢)交换结果对比

图7 VPP夏季需求响应前后电负荷

图8 VPP冬季需求响应前后电负荷

根据模型运行结果,参考图6分析可得,VPP在夏季受季节性风光出力特点影响形成的电量缺口,更倾向于由初始投资成本高但能效更高的燃气轮机提供,相比其他季节与主网交换电量较低,电解槽出力最小,储能全天平均蓄电率为29.15%。图7中柔性负荷参与了需求响应,通过负荷削减平抑了峰谷差,柔性削减量为10.63 MW·h,且平均负荷削减率为4.91%。结合表9综合最优的成本数据可得,VPP的碳排放量对比情景1减少10.81%,运行成本对比情景2减少2.27%,同样保证了VPP的经济性和低碳性。

根据模型运行结果,参考图6分析可得,VPP在冬季增加了主网购电购氢的比例,新增的季节性风电不足以填补用户电负荷和汽车氢负荷,相对于其他季节电解槽出力时长增多,储能全天平均蓄电率为27.32%,图8中展示了柔性负荷削减量为10.7 MW·h,平均负荷削减率为5%,结合图5可知本文购建的需求响应模型在保证用户用电稳定性时,峰时段适当的柔性负荷削减使购电成本降低。结合表9综合最优的成本数据可以分析得出,VPP碳排放量对比情景1减少9.03%,运行成本对比情景2减少2.02%,与其他季节情景一致,综合最优目标能兼顾经济和环境目标双重需求。