极端风暴下的海上风电制氢联合运行系统爬坡控制策略
2024-04-02张培杰陈春宇任必兴臧天磊戴雪梅张晓
张培杰, 陈春宇,任必兴,臧天磊,戴雪梅,张晓
(1.中国矿业大学电气工程学院, 江苏省徐州市 221116;2. 国网江苏省电力有限公司电力科学研究院,南京市 211103;3. 四川大学电气工程学院, 成都市 610065;4. 上海电力大学自动化工程学院, 上海市 200090)
0 引 言
为构建新型电力系统,我国在新能源禀赋优良且具备可持续开发条件的地区,大力推进新能源基地化开发。海上风电因其大规模发电潜力、优质风资源和对土地资源的低依赖性,在“十四五”可再生能源建设中占据重要位置[1-2]。为提升风电消纳水平,避免大规模弃风问题发生,考虑“风电+储能”的风储联合运行系统受到广泛关注[3]。其中,氢能作为一种高能量密度清洁能源,存储与运输的经济效益通常优于电能[4]。海上风电制氢联合系统是风储联合运行系统今后的重要发展方向之一。近年来,全球气候变暖导致海上风暴等极端气象事件频繁发生,亟需研究海上风电制氢联合系统在极端气象事件下的安全运行策略。
作为一种新型风储联合运行系统,海上风电制氢联合系统的研究重点主要包括:系统储能容量优化配置[5-9]、优化调度[10-14]和电力市场竞价[11]等方面。文献[5]采用聚类算法得到典型的风电-负荷场景,并构建了综合考虑系统年运行成本、设备年化投资成本和维护成本的风-氢耦合系统容量优化配置方案。文献[6]采用区间优化理论确定风电制氢系统最优容量配置区间。文献[9]考虑了动态电价对容量配置的影响,提出了以单位制氢成本最低为目标的储能与制氢单元容量配置方案。从系统调度层面出发,文献[10]提出了碳减排机制下的风氢联合调度策略,提升了低碳经济效益。从资源角度出发,风电制氢联合运行系统可以参与能量或者辅助服务市场获得收益。然而,由于风电和电价的不确定性,会影响风电制氢联合运行系统的可靠性。为此,文献[11]提出了基于分布式机会约束规划方法的日前能量市场竞价策略,可有效降低不确定性风险。风电制氢联合运行系统中的风电场和制氢站可能分属不同运营主体,二者参与市场存在获利协调问题。为此,文献[14]利用多智能体强化学习方法,设计了联合收益最大化模型。上述研究显著提升了风电制氢联合运行系统的经济效益。然而,在极端气象条件下如何避免海上风电制氢联合运行系统爬坡,保证主网安全运行,仍值得进一步深入研究。
近年来,研究人员针对台风等极端气象条件下的电网调度或防控展开研究。文献[15]预测海上风机梯次停运时间以延缓风电功率爬坡。文献[16]模拟了台风下电力系统设备故障状态,对不同风电渗透率下的电网进行多时间尺度调度。文献[17]考虑了风电不确定性,建立了基于极限场景的两阶段鲁棒规划模型,提高了配电网在极端情况下的可靠性。文献[18]考虑了台风事件对海上风电场储能配置的影响,提出了考虑风电不确定性的储能容量优化配置方法。上述研究主要侧重台风导致的风机故障与系统安全运行问题研究,对台风天气下海上风电制氢联合系统的爬坡及其对系统的影响考虑不足。
在常规气象条件下,海上风电制氢联合运行系统给周边海岛负荷供电;同时,通过海底电缆接入岸上主网,在满足储氢需求的同时,将富余风电输送至岸上主网。然而,在极端风暴环境下,海上风电制氢联合运行系统因风电功率的剧烈波动可能出现并网功率爬坡问题。基于此,本文分析了海上风电制氢联合运行系统的爬坡自抑制特性,并给出了不确定性情况下基于机会约束的爬坡平抑控制策略及其最优置信度选取方法,实现了成本与风险控制的有效平衡。提出了一种考虑风电不确定性的爬坡控制策略。首先,通过定量描述风电制氢联合运行系统与传统海上风电场在极端风暴下的爬坡特征,分析了海上风电制氢联合运行系统对爬坡的自抑制能力。然后,构建考虑源-储-荷运行特性的爬坡控制模型,并给出考虑风电不确定性的机会约束模型形式。紧接着,通过机会约束转换求解确定性控制模型,得到爬坡控制资源在风暴来临前后的调度出力方案;最后,通过客观权重赋权法(criteria importance though intercrieria correlation,CRITIC)-优劣解距离法((technique for order preference by similarity to ideal solution, TOPSIS)进行多属性决策(multiple attribute decision making,MADM)。仿真结果表明,同样是采用协调优化爬坡控制方法,相较于风电场,由于电解系统对风电功率的吸收作用,海上风电制氢联合运行系统无需弃风,直接使用电解系统抑制极端风暴过境前后引发的功率波动,提升了风电消纳水平。同时,通过选取合适的置信度,所提考虑风电不确定性的爬坡控制策略可以有效兼顾成本控制与风险抑制需求。
1 极端风暴下的海上风电制氢联合运行系统的爬坡特性分析
1.1 极端风暴对海上风电制氢联合运行系统爬坡的作用机理
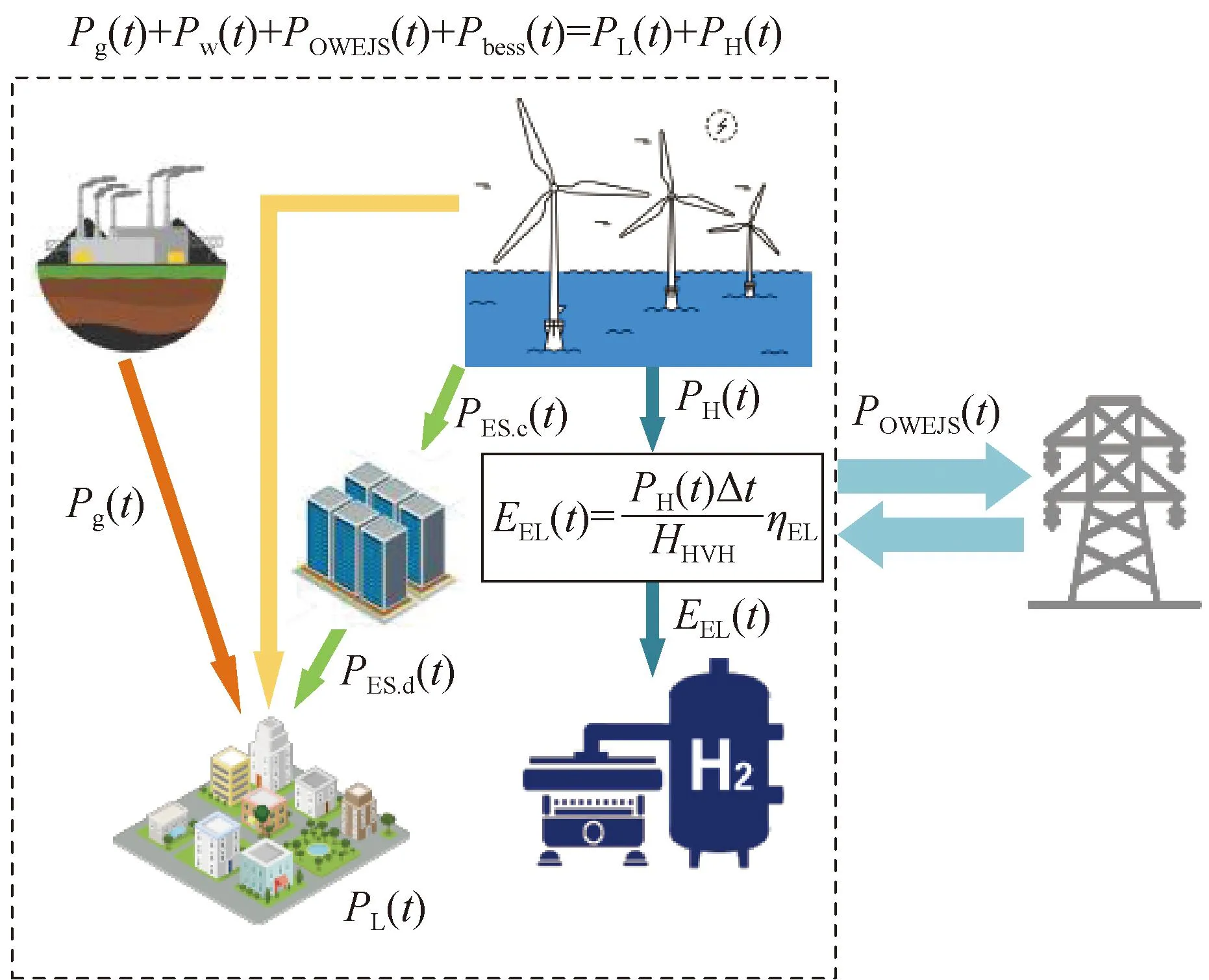
并网运行的海上风电制氢联合运行系统(offshore wind-electrolysis joint system, OWEJS)结构如图1所示。

图1 海上风电制氢联合运行系统基本结构
OWEJS主要由风电场、电解系统及其配套系统(压缩机、储氢罐等)构成,海上风电系统向主网供电同时利用剩余风电功率向储氢系统供电,其向主网的净注入功率POWEJS为:
POWEJS=PW-PH
(1)
式中:PW表示海上风电总预测功率;PH表示用于电解制氢的风电功率。在极端风暴过程中,OWEJS净注入功率与风速的关系可表示为:
(2)
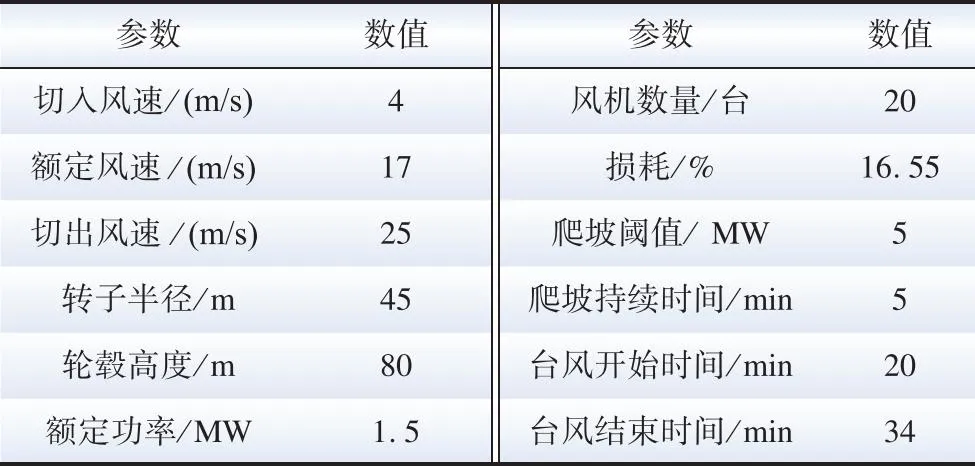
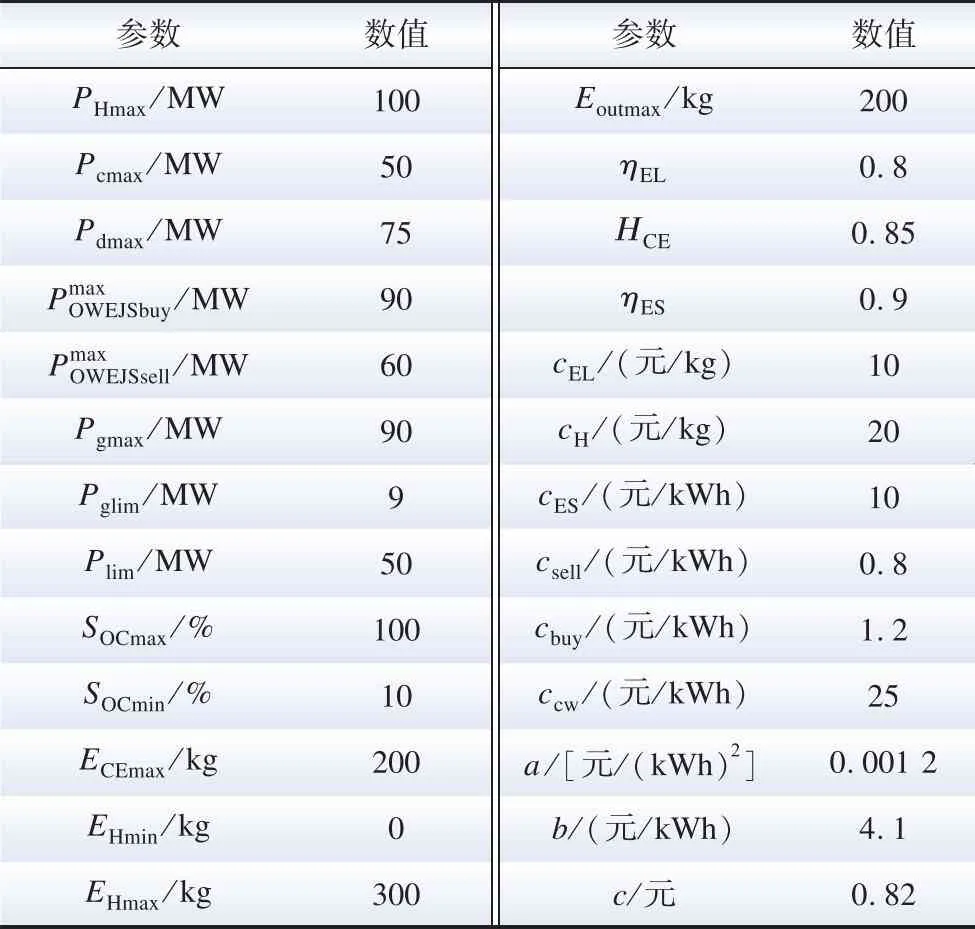
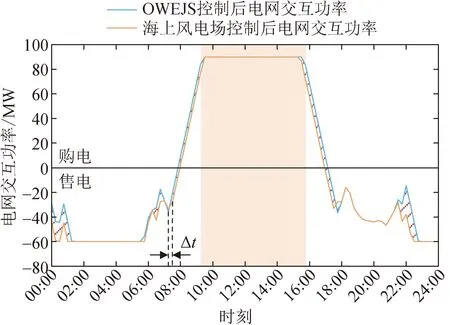
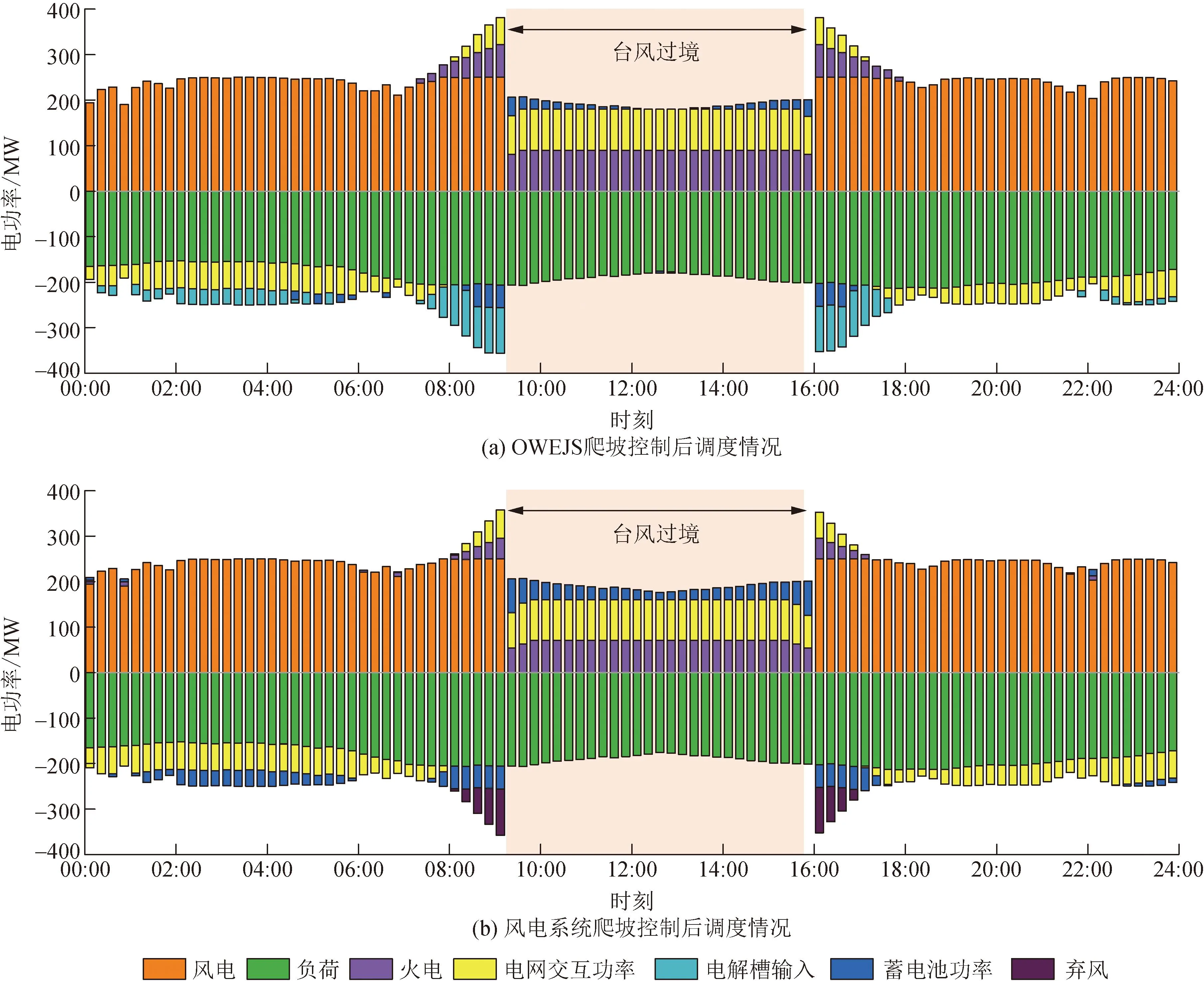
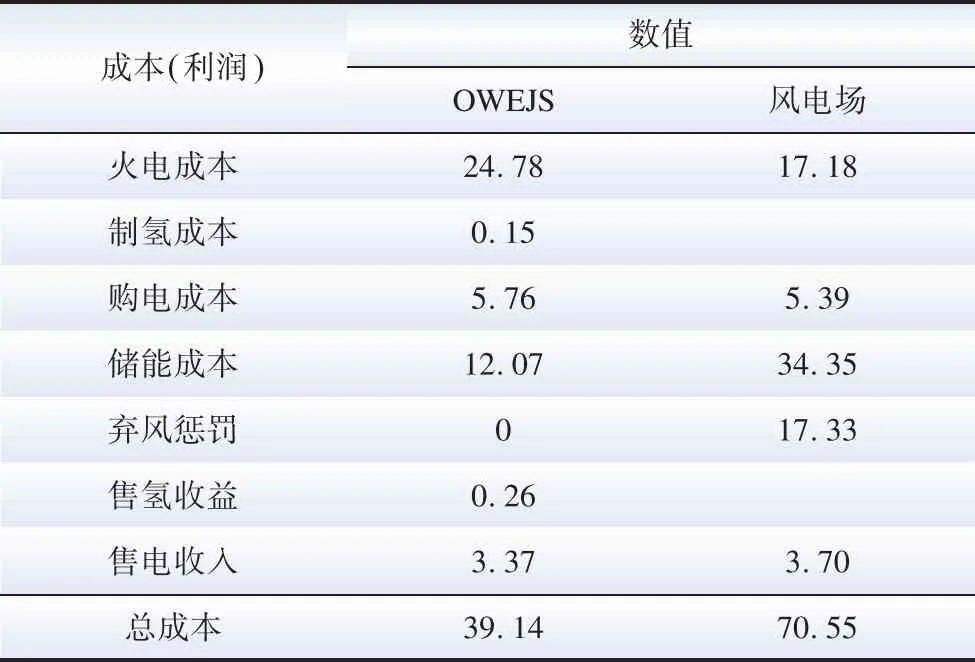
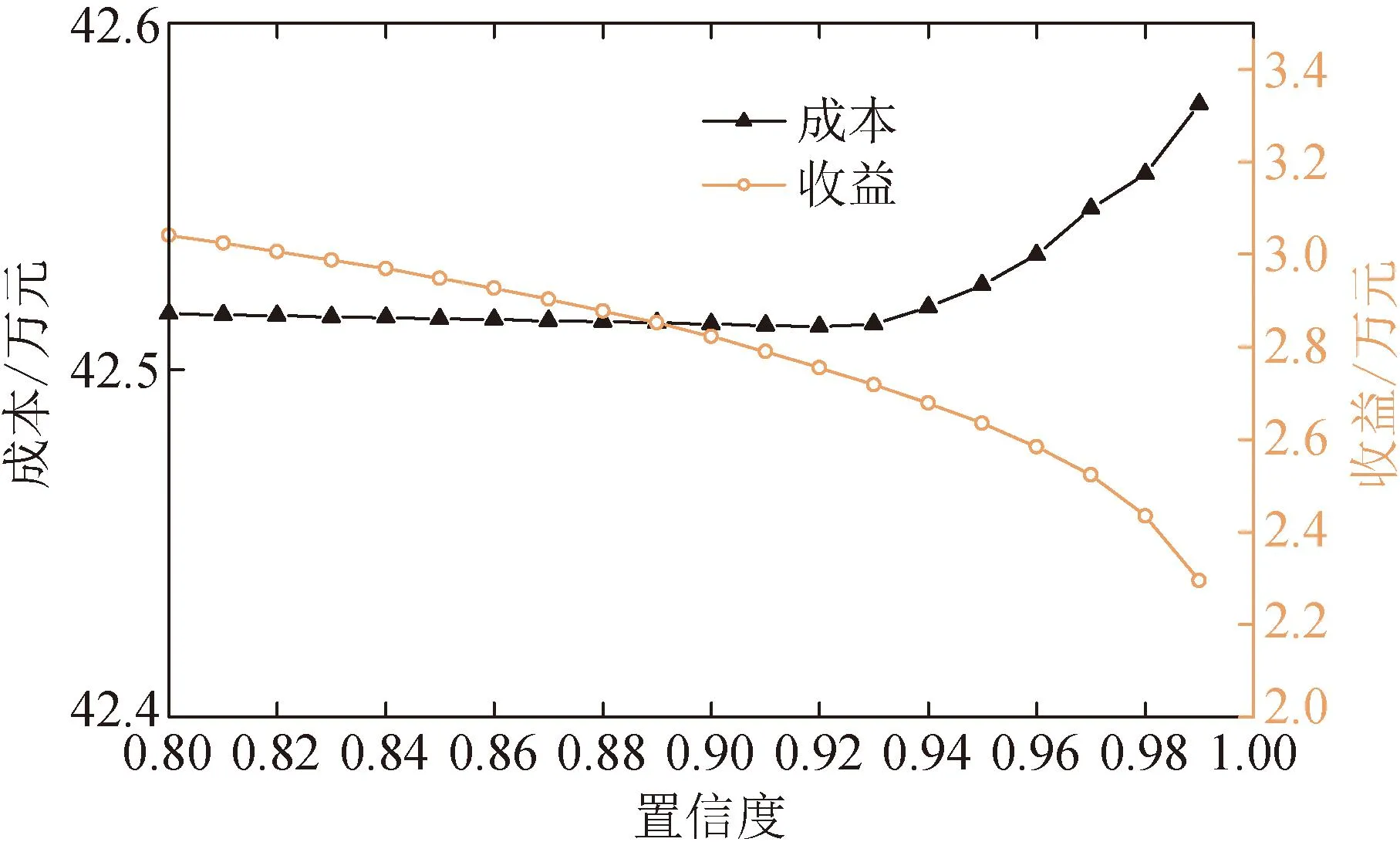
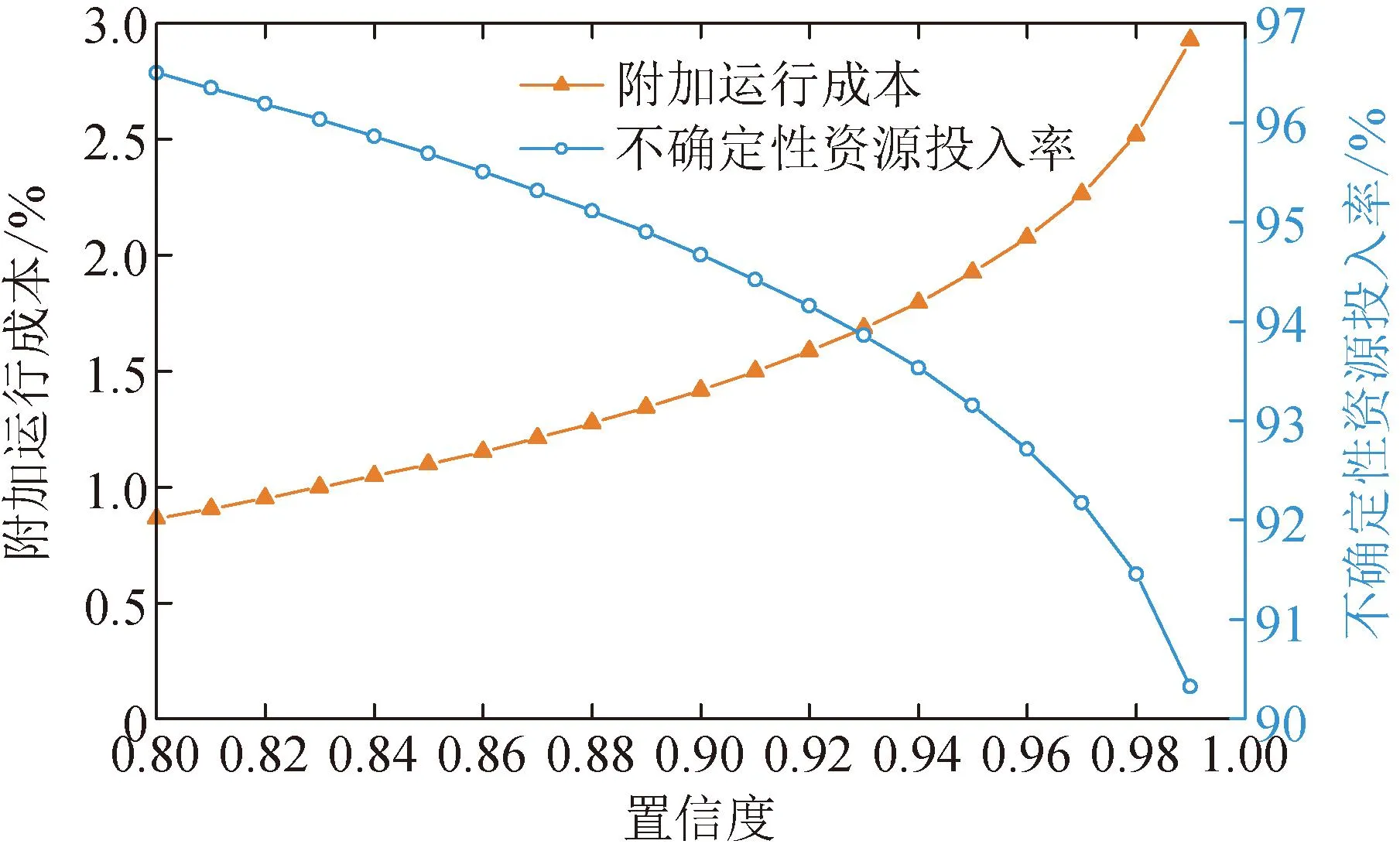
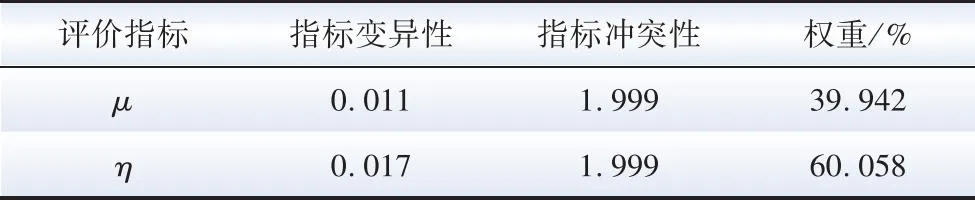
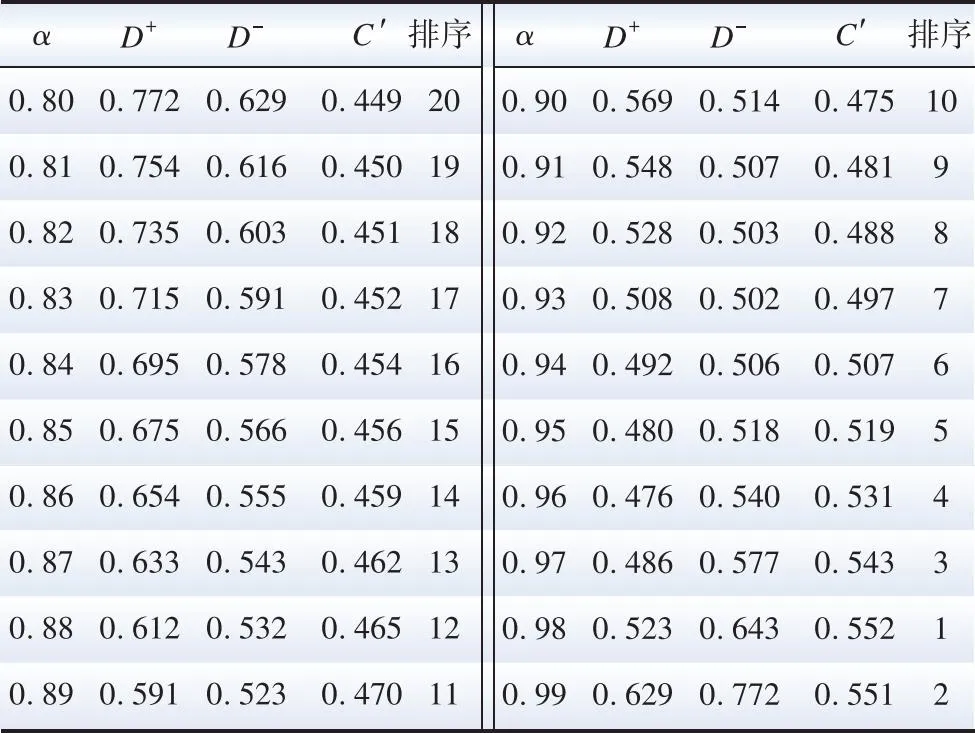
式中:POWEJS(v)表示风速v下的净注入功率;PH(v)表示风速v下向电解系统注入的制氢功率;Prate表示海上风电场的额定功率;ρ表示空气密度;Cp为气动性函数;r为叶片半径;vin为海上风电场的切入风速;vstart为电解系统启动风速;vrate代表额定风速;vout代表海上风电场的切出风速。令风暴来临前后的风速分别为v0(vstart (3) 式中:ΔPH为制氢风电功率变化量。 ΔPH=PH(v1)-PH(v0) (4) 由式(3)可知,通过控制高风速v1下的制氢功率PH(v1)超出低风速v0下的制氢功率PH(v0),可以利用正的ΔPH抵消部分风电功率增加,从而抑制OWEJS上爬坡。当v1超过切出风速vout时: (5) 可以利用制氢功率PH(v0)来抵消部分风电功率减少,从而抑制OWEJS下爬坡。 以Composite IEC Class I风电场为基础,构建模拟OWEJS与海上风电场实际运行的仿真系统,得到台风来临前后的系统功率曲线。仿真关键参数如表1所示。台风风力为12~13级,风速范围为28.5~41.5 m/s。台风过境时间为17~30 min。台风实际风速数据由YanMeng风场模型计算得出。 表1 仿真关键参数 爬坡事件定义为: ΔPx=|Px(t+Δt)-Px(t)| (6) 式中:Px(t)为t时刻系统功率;x表示不同系统(海上风电场系统或OWEJS);Δt为爬坡持续时间,爬坡阈值设为Plim=20%Prate[19]。 通过式(2)所示的OWEJS功率分段函数,模拟出相同风速条件的海上风电场(即不考虑制氢环节PH(v)的特殊OWEJS)与OWEJS出力曲线,如图2所示。由图2可知,尽管台风过境前(0~17 min)与过境后(30~48 min)系统(OWEJS和风电场)出现并网功率波动。然而,由于风速波动幅度较低(7~12 min),系统功率变化(OWEJS对应的ΔPOWEJS1=1.72 MW和海上风电场对应的ΔPw1=3.99 MW)远低于爬坡事件功率变化率阈值Plim。因此,在正常风速变化情况下,系统不会发生爬坡事件。 图2 极端风速下的系统爬坡特性 当台风来临时(17~22 min),风速由21.3 m/s骤增到45.5 m/s,导致风电切机,海上风电场功率由额定出力2.50 MW骤减至0 MW,发生如图2蓝色虚线箭头所示的下爬坡事件。由于OWEJS通过制氢系统吸收部分功率,使得台风来临时OWEJS功率变化(蓝色实线箭头所示,ΔPOWEJS2=1.76 MW)小于海上风电场功率变化(ΔPw2=2.50 MW)。 在台风结束时段30~35 min,风速由26 m/s减至切出风速以下,至21m/s附近。此时,海上风电场输出功率由0 MW骤增至额定功率。由图2可知,在台风结束时段内由于制氢系统的吸收作用,使得OWEJS功率变化(ΔPOWEJS3=1.76 MW)小于海上风电场(ΔPw3=2.50 MW)。 综上仿真分析表明,OWEJS通过控制氢功率的变化量ΔPH,对并网功率爬坡具备抑制作用。为了实现爬坡控制经济效益最优,本文进一步提出一种源荷储协调爬坡控制策略。 本文提出的源荷储协调爬坡控制框架如图3所示。OWEJS、火电系统与储能系统供应微网负荷并与主网实现功率交互。 图3 源荷储协调爬坡控制框架 2.1.1 电解系统模型 电解槽在t时段产生氢气量EEL(t)为[20]: (7) 0≤PH(t)≤PHmax (8) 式中:PH(t)代表t时刻输入电解槽功率;PHmax代表电解槽输入功率上限;ηEL为电解槽制氢效率,本文选用碱性电解槽,取67%~82%;HHVH为氢的热值,通常取39.4 kW/kg。 电解槽产生的氢气经压缩后输送到储氢站,压缩机模型可表示为: ECE(t)=EEL(t)·ηCE (9) 0≤ECE(t)≤ECEmax (10) 式中:ηCE为压缩机效率;ECE(t)为t时刻压缩机输出的氢气量;ECEmax为压缩机输出氢气量上限。 储氢站数学模型可表示为[21]: EH(t)=EH(t-1)+ECE(t)-Eout(t) (11) EHmin≤EH(t)≤EHmax (12) 0≤Eout(t)≤Eoutmax (13) EH(T)=EH(0) (14) 式中:EH(t)为t时刻储氢罐的储存量;Eout(t)为t时刻储氢罐的售出量;EHmax与EHmin分别表示储氢罐容量的上下限;Eoutmax为储氢罐的最大售出量;EH(T)=EH(0)表示爬坡控制周期初始与末端时刻储氢罐的储存量相等。 2.1.2 储能系统模型 采样同时考虑充放电功率与荷电状态的储能电池模型[22-23]: (15) SOCmin≤SOC(t)≤SOCmax (16) 0≤PESc(t)≤δc(t)·Pcmax (17) 0≤PESd(t)≤δd(t)·Pdmax (18) δc(t)+δd(t)≤1 (19) SOC(T)=SOC(0) (20) 式中:SOC(t)为t时刻储能电池的蓄电量;PESc(t)与PESd(t)代表t时刻储能电池的充放电功率;ηES为充放电效率;Pcmax与Pdmax代表充放电功率上限;SOCmax和SOCmin代表储能电池电荷量上下限;δc(t)与δd(t)代表充放电状态,为0-1变量,式(19)确保储能电池充放电不会同时发生。 2.1.3 并网功率模型 当微网内总体发电功率大于负荷时向电网售电;反之则向电网购电满足负荷需求。微网与电网功率交互模型如下: (21) (22) δbuy(t)+δsell(t)≤1 (23) 2.1.4 爬坡控制目标函数 构建考虑成本最小化的爬坡控制目标函数。由于建设储能电池、储氢等设备的成本固定,且日常维护成本较小,因此在本文中忽略不计[24-26]。 (24) 式中:T表示爬坡控制总时段;Cg为火力发电成本;CEL为制氢成本;Cbuy为购电成本;Ccw为弃风惩罚成本;CES为储能成本;CH为售氢所得收益;Csell为售电收益,具体地: (25) CEL=cELEEL(t) (26) Cbuy=cbuyPOWEJSbuy(t) (27) Ccw=ccwPcw(t) (28) CES=cES|Pbess(t)| (29) CH=cHEout(t) (30) Csell=csellPOWEJSsell(t) (31) 式中:Pg(t)为t时刻火电出力;Pcw(t)为t时刻OWEJS弃风功率;Pbess(t)为t时刻储能充放电功率;a、b和c为火电输出功率成本系数;cEL、cbuy、ccw、cES、cH和csell分别为t时刻电解槽的单位制氢量成本、单位购电成本、单位弃风惩罚成本、单位储能成本、售氢单价以及售电单价。 2.1.5 爬坡控制约束条件 爬坡控制约束包括2.1.1—2.1.3节给出的电解系统模型式(7)—(14)、储能系统模型式(15)—(20)以及并网功率模型式(21)—(23)。同时,爬坡控制约束还包括: 功率平衡约束: Pg(t)+Pw(t)+POWEJS(t)+Pbess(t)≥PL(t)+PH(t) (32) 式中:Pw(t)为t时刻海上风电场的出力预测值;PL(t)代表t时刻微网负荷预测功率。 弃风功率约束: 0≤Pcw(t)≤Pw(t) (33) 并网功率爬坡约束: |POWEJS(t+Δt)-POWEJS(t)|≤Plim (34) 火电机组运行约束: 0≤Pg(t)≤Pgmax (35) |Pg(t+Δt)-Pg(t)|≤Pglim (36) 式中:Pgmax为火电出力上限;Pglim为火电机组爬坡阈值。 由于风电具有随机与波动性,2.1节适用于固定参数的确定性模型可能无法很好评估由风电波动性带来的弃风以及失负荷等风险。为此,本文将受风电不确定性影响的功率平衡约束式(32)转换为满足一定置信度的机会约束,使得爬坡控制模型兼顾经济性和鲁棒性: Pr{Pg(t)+Pw1(t)+POWEJS(t)+Pbess(t)≥PL(t)+PH(t)+Pcw(t)}≥α (37) Pw1(t)=Pw(t)+ξ (38) 式中:Pr{·}为{}中条件成立的概率;α为置信度;Pw1(t)为t时刻风电实际出力;ξ为风电预测误差。 机会约束式(37)无法直接求解,本文令ξ服从正态分布[27],将式(37)转化为[28]: PL(t)+PH(t)+Pcw(t)-POWEJS(t)-Pbess(t)-Pg(t)≤Pw(t)+Γα (39) 式中:Γα为风电预测误差累计概率分布函数Φ的逆函数Φ-1在1-α的函数值: Γα=Φ-1(1-α) (40) 在考虑风电不确定性爬坡策略的基础上,本文进一步提出基于CRITIC-TOPSIS法的最优置信度综合评价模型对不同置信度下系统优化结果进行评价,得到最适合调度中心的置信度。 2.3.1 置信度评价指标 本文选用的置信度评价指标为不同置信度下系统附加运行成本μ与不确定性资源投入率η。 μ与η计算方法如下: (41) (42) 式中:FCCP(α)为不同置信度α下系统成本。μ越大表示不确定性(考虑机会约束的)爬坡控制相对于确定性(不考虑机会约束的)爬坡控制成本变化越剧烈,系统抵抗风电不确定性产生的附加成本越高[29];η越高代表不确定性资源(风电)发生的违约风险越高。 2.3.2 CRITIC-TOPSIS法原理 为了衡量指标(μ与η)在α决策过程中的重要程度,需要对其赋权。指标权重的确定方法主要有主观赋权法、客观赋权法。 由于主观赋权法过多依赖人为偏好,客观性较弱,故采用CRITIC法求出μ和η在评价模型中的权重[30]。然后,使用TOPSIS方法,结合CRITIC求出的权重值,计算不同置信度下综合评价指标。 CRITIC是一种为多维度决策指标提供比例权重的方法[31],既能反映各指标下数据结果的差异波动程度,又能降低相关性高的指标在评价时造成的重复性。TOPSIS是一种通过对多个评价对象与理想解贴近度进行优劣排序的多属性决策分析综合评价方法[32-34]。 将不同置信度作为评价决策集,比较不同指标与正负理想距离的相对接近度,根据相对接近度确定最优置信度。CRITIC-TOPSIS法主要步骤如下[35]: 第一步:设原始决策矩阵X=(xij)n×m,为消除因量纲不同对评价结果造成的影响,对各指标进行无量纲化处理,得到标准化矩阵X′=(x′ij)n×m。 第二步:计算第j个指标的标准差Sj来表示各指标内取值波动差异情况,如下所示: (43) 第三步:通过不同指标之间的相关系数rij,计算指标冲突性系数Rj,如下所示: (44) (45) 第四步:根据指标冲突性系数,求第j个指标在整个评价指标体系中的信息量Cj,信息量越大其在评价过程中作用就越大: Cj=Sj·Rj (46) 第五步:计算客观权重wj: (47) 第六步:计算标准化矩阵Z: (48) (49) (50) 第八步:计算各置信度与最优置信度的相对接近值C′j: (51) 结合上述爬坡控制模型与评价模型,本文所提的源荷储协调爬坡控制策略流程如图4所示。 图4 爬坡控制策略流程图 本节使用实际数据对第2节提出的爬坡控制模型进行仿真算例验证。图5(a)所示的源荷数据均来自比利时电网开源数据[36];时间步长为15 min,风速[37]曲线见图5(b);根据我国对并网风电爬坡率要求[38],并网爬坡率限制Plim取15 min变化率不超过50 MW。其他具体参数见表2[12,39]。为了比较OWEJS与海上风电场的爬坡控制效果,本文令OWEJS与海上风电场(除电解系统外)的系统参数完全相同。 表2 算例仿真参数 图5 源荷数据曲线 本文采用Yalmip(版本R20210331)与Gurobi(版本10.0.2)求解式(7)—(40)。电脑配置为Intel(R) Core(TM) i5-12600KF CPU @ 3.70 GHz ,内存RAM为16 GB。 图6给出OWEJS与海上风电场爬坡控制后的并网功率曲线。定义向系统注入功率为正,从系统吸收功率为负,得到OWEJS与海上风电场爬坡控制后各机组出力如图7所示。其中,Y轴正半轴为风电功率、向电网购电功率、火电功率以及储能电池的放电功率;Y轴负半轴为负荷预测功率、向电网售电功率、储能电池充电功率、弃风功率以及电解槽从OWEJS系统吸收的功率。图中橙色阴影(09:15—15:45)代表台风过境时段。 图6 不同系统爬坡控制后电网交互功率 图7 不同系统爬坡控制前后调度情况 图6蓝色实线所示的OWEJS并网功率曲线分为售电阶段(00:00—07:15与17:45—24:00)、售电-购电过渡阶段(07:15—09:30与15:30—17:45)与购电阶段(09:30—15:30)。在00:00—07:15和17:45—24:00,由于风电出力高于负荷且风电成本低于火电与储能,火电与储能没有出力。供给负荷后的富余风电功率直接转化为售电功率传输给主网;同时,在01:15—05:45时段,由于富余风电功率超过售电功率上限,并网功率维持在60 MW,超过上限的风电功率部分由电解槽吸收(如图7(a)中01:15—05:45浅蓝色柱状图所示)。在台风发生前08:00—09:30,台风即将过境,火电由于爬坡限制提前开始出力,微电网由向系统售电过渡为从系统购电状态。同时,由于爬坡控制的作用,并网功率的变化率保持在阈值50 MW/(15 min)以内。在台风过境阶段09:30—15:30,风速从21.3 km/s陡升至35.5 km/s超出切出风速,风电出力快速降低至0 MW,火电与储能增加出力以供给负荷需求;由于微电网的购电成本低于火电与储能,因此,并网功率在保证爬坡限制的前提下增至购电功率上限(如图7(a)中10:00—15:30黄色柱状图所示)。在台风结束阶段15:30—16:00,风速由30.3 km/s减小到23.3 km/s,同时风电功率由0 MW骤升至额定功率,此时并网功率由购电阶段过渡到售电阶段,由于并网功率爬坡限制,购售电状态无法瞬间转换,在风电功率达到额定状态下仍存在短时间购电(如图7(a)中16:00—17:00黄色柱状图所示),此时超出负荷功率的部分功率向电解槽提供功率(如图7(a)中16:00—17:00的浅蓝色柱状图所示),完成对风电的完全消纳。 图6橙色实线所示的海上风电场并网功率同样可分为售电阶段(00:00—07:15与17:30—24:00)、售电-购电过渡阶段(07:15—09:30与15:15—17:30)与购电阶段(09:30—15:15)。不同机组的功率变化规律与OWEJS大致相同,主要区别包括: 1)海上风电场产生富余的风电功率(风电-负荷)对主网的售电功率达到上限后,转而向储能系统放电(如图7(b)中01:00—06:00的蓝色柱状图所示)。而在OWEJS中,由于储能系统的单位充放电成本超过电解槽,因此OWEJS优先使用电解槽储存富余风电。 2)当储能系统蓄电量达到上限后,多余的风电只能通过弃风来保证系统功率平衡,同时两系统都通过设置弃风惩罚来减少弃风。所以海上风电场会尽量延迟“售电-购电过渡阶段”开始时间来减少因储能电池饱和产生的弃风量(如图6中Δt=15 min)。而OWEJS优先使用电解槽储存富余风电,储能电池不会饱和,不会产生弃风,可以实现风电的完全消纳。由于售电与售氢均可产生利润,而充放电都需要成本,同时购电成本也要小于储能放电成本,所以OWEJS会提前进入“售电-购电过渡阶段”以减小储能电池的运行成本。 3)OWEJS的火电总成本与购电总成本均大于风电场,但储能成本小于风电场,同时OWEJS没有弃风。在爬坡控制周期内,OWEJS与海上风电场中的火电机组与购电主要发生在其“购电阶段”,由于储能的单位充电成本高于电解槽,富余风电主要供给电解系统,所以在“购电阶段”为平衡微网负荷主要表现为电网购电以及火电出力(如图7(a)中09:15—15:45Y轴上半轴柱状图组合所示)。而海上风电场在“购电阶段”富余风电主要通过储能系统储存,所以在“购电阶段”,风电场的储能出力要大于OWEJS。在“购电阶段”初期与末期,海上风电场由于火电出力爬坡限制,使用储能放电并向电网购电来平衡微网负荷,此时储能出力略大于火电出力(如图7(b)中 09:15—9:45与15:30—15:45Y轴正半轴柱状图组合所示);当购电达到上限之后,由于火电出力成本小于储能单位成本,此时火电出力大于储能出力。综上分析可知,OWEJS在购电阶段(台风过境过程)的购电功率与火电功率大于海上风电场,同时其储能放电功率要小于海上风电场,符合表3中不同资源的成本数据变化规律。 表3 不同系统下各能源系统运行成本与利润 不同置信度下系统调度成本与收益变化情况如图8所示。不同置信度下系统附加运行成本μ与不确定性资源投入率η如表4和图9所示。 表4 不同置信度下系统方案 图8 置信度对经济效益的影响 图9 置信度对评价指标的影响 图8与9显示,OWEJS的调度成本伴随置信度α的降低而降低。α越低,收益和风电利用率越高。主要因为置信度越低,系统的保守性越弱,不确定性风电参与程度提升,此时火电机组出力与电网购电功率减小,整个系统成本降低,系统不确定性风险增加。 由表4与图9可知,μ和η随α递增呈现相反的变化趋势,μ随α增加而增加,η随α增加而减小;无法找到同时满足μ和η最小的α。调度中心希望通过选择合适的置信度,可以将系统风险控制在可以接受的范围内,同时减少系统成本,从而协调系统的可靠性与经济性。基于此,通过2.3节所述评价方法对不同置信度下的系统综合运行性能进行评价。 基于CRITIC-TOPSIS法的权重与最优置信度结果如表5和6所示,系统总成本和风险的指标权重分别为39.942%、60.058%。表6显示当置信度取0.98时,综合评价指标达到最优值。 表5 CRITIC法权重计算结果 表6 不同置信度下系统风险排序 本文考虑海上风电制氢联合运行系统在极端风暴下面临的并网功率爬坡问题,提出了考虑风电不确定性的源荷储协调爬坡控制策略,得到如下结论: 相较于海上风电场,海上风电制氢联合运行系统在源荷储协调爬坡控制的过程中,可以有效降低弃风率和弃风惩罚成本。在新能源消纳目标优先级与单位弃风惩罚成本较高的情况下,海上风电制氢联合系统的爬坡控制经济效益高于海上风电场。 随着置信度的递增,系统对不确定性能源的投入越低,同时抵抗不确定性而产生的附加成本越高。最后通过CRITIC-TOPSIS对不同置信度下系统成本-风险综合指标进行评价发现,调度中心选择置信度为0.98时可以在多属性决策下获得系统综合指标最优。1.2 海上风电制氢联合运行系统的爬坡特性分析

2 极端风暴下的海上风电制氢联合运行系统爬坡控制
2.1 源荷储协调爬坡控制模型
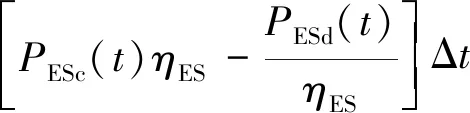

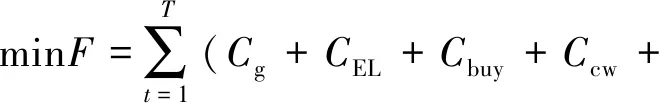
2.2 考虑风电不确定性的爬坡控制策略
2.3 基于CRITIC-TOPSIS法的最优置信度评价模型
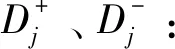


3 算例分析

3.1 风电制氢联合运行系统与风电场的爬坡控制效果对比分析
3.2 考虑不确定性的风电制氢联合运行系统爬坡控制结果分析

4 结 论
