基于挠曲线方程的某车载雷达天线质心估算方法*
2024-03-30贺照鹏
贺照鹏
(上海航天电子技术研究所,上海 201109)
引 言
在工程上,准确确定负载的质心位置对承载结构的受力分析、设计校核和实际使用都至关重要。物体质心估算常用的方法有理论计算法和实物测量法。理论计算法可以初步地对物体质心进行估计,然后开展前期受力分析等设计工作,但对于组成复杂的产品,计算工作量偏大;实物测量法可以更精准地确定产品质心,用以验证理论计算的结果,评估实际使用时的受力情况。对于大型雷达天线,实物测量需要借用专用仪器设备、工装及场地,具体工程实现有一定的局限性。本文介绍了一种适用于大型雷达天线的质心位置估算方法,借助悬臂梁所受集中力的数学模型,根据悬臂梁受力变形的挠曲线方程估计雷达天线质心。
实际工程中一般采用挠曲线方程解决梁的变形问题,国内学者在挠曲线方程方面进行了诸多研究。文献[1–2]通过积分法对梁的挠曲线方程进行精确推导,得到了精确的微分方程。文献[3]依据弹塑性分区最小势能原理,对梁的挠曲变形进行了求解。在雷达转塔系统刚强度设计方面,文献[4]建立了天线基座平台的多体动力学模型,得出了天线刚性运动规律及基座板角度变化规律;文献[5]对某转台方舱的刚强度进行有限元分析,通过仿真结果确认该转台方舱骨架强度和刚度满足设计要求。
1 挠曲线近似微分方程
如图1所示,跨度为L的悬臂梁在纵向对称面内的外力F的作用下,将产生平面弯曲,变形后梁的轴线将变成一条光滑的平面曲线,称为梁的挠曲线。梁的横截面形心在垂直于x轴方向上的线位移即为挠度w;横截面对其原来位置的角位移即为转角θ。

图1 挠曲线示意图
挠曲线近似微分方程的使用条件为:1)纯弯曲梁或细长梁的横力弯曲;2)小变形,即变形量远小于构件的原始尺寸(梁的跨度),这样可以按照构件的原始尺寸计算受力平衡;3)梁的应力不超过材料的比例极限(弹性范围内)。挠度的近似微分方程如下:
式中:w为梁的挠度;E为材料的弹性模量;I为截面惯性矩;EI即为抗弯刚度;x为悬臂梁上某点距固定点的距离;M(x)表示悬臂梁上弯矩M是x的函数;C1、C2为常数。通过测量不同受力位置下梁的转角,建立方程组,即可求得受力位置距固定点的距离。
2 转塔系统数学模型
某车载雷达转塔系统示意图如图2所示,由方位转台、转塔、雷达天线和俯仰电动缸组成。转塔对雷达天线起到承载的作用,方位转台与转塔之间采用圆周方向均布的螺栓相连,雷达天线通过俯仰电动缸及俯仰轴与转塔连接。雷达天线可以绕俯仰轴旋转0◦∼70◦,当俯仰角度发生变化时,雷达天线的质心位置也会发生偏移,转塔产生的变形量和转角也随之变化。转塔上有一处基准面,可以放置合像水平仪用以测量转塔的绝对角度;在雷达天线上,可以使用激光跟踪仪测量雷达天线与大地的绝对角度;雷达天线的相对俯仰角度可以通过俯仰角度编码器测得。
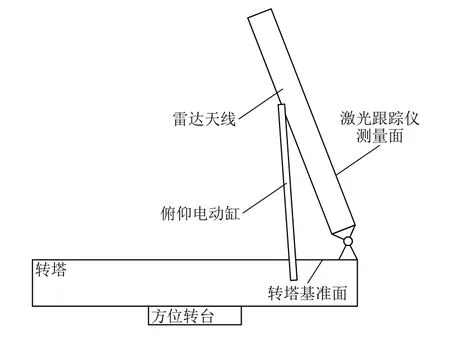
图2 转塔系统示意图
转塔是将方钢管焊接成规则形状的骨架后,在四周安装蒙皮而成,内部设备近似对称排布,整体可以简化为一个等截面梁,满足上节挠曲线近似微分方程的使用条件。因此,可将转塔看成以回转中心为固定点的悬臂梁,雷达天线的重力为加载在悬臂梁一端的集中力,以此建立转塔系统的数学模型。同时,雷达天线在设计时都采用对称设计,即天线宽度和厚度方向的质心位置都近似位于对称轴上,因此只需确定长度方向的质心位置。
转塔的重力一直存在,对于整个系统的变形,转塔重力不可忽略,可将其看成整个系统中的一个质点,由此得到图3所示的转塔系统受力图。悬臂梁上的力矩分布为一个分段函数,函数方程为:

图3 转塔系统受力图
式中:F为雷达天线的重力;G为转塔的重力;l1为转塔质心距回转中心距离;l2为雷达天线质心距回转中心距离。
将式(2)代入式(1)后,对¨w(x)积分得:
式中,θ(x)表示转角θ是x的函数。由于系统变形为小变形,因此转角θ近似等于挠曲线的曲率。
式(3)为转角微分方程的通解,两个常量的确定需代入悬臂梁的边界条件(固定端的挠度和转角均为0)和连续条件(挠曲线应连续且光滑)。微分方程的边界条件为:
代入式(3)得到C1、C2两个常量:
代入式(3),转角微分方程的特解为:
将雷达天线拆除后,系统中只保留转塔重力,此时悬臂梁的力矩方程为:
式中,M′为此时系统所受弯矩。
按上述过程推导出系统转角微分方程的特解为:
式中:θ′为此时系统的转角。
式(6)与式(8)相减即可得到去除转塔重力等其他外界条件的影响,只有雷达天线重力时系统的转角方程:
转塔系统坐标示意图见图4,以转塔系统上平面为x轴、转塔系统回转中心为y轴建立坐标系。状态1为雷达天线的运输状态,雷达天线与转塔上平面平行。选取雷达天线理论俯仰角50◦(状态2)和70◦(状态3)两个工作状态,分别测得转塔的变形角度,代入式(6);拆除雷达天线后,再测量一次转塔的变形角度,代入式(8)得:

图4 转塔系统坐标图
式中:α1为不计转塔重力影响下雷达天线处于状态2时转塔的变形角度;α2为不计转塔重力影响下雷达天线处于状态3时转塔的变形角度;β为不计雷达天线重力影响下转塔自身重力产生的变形角度;θ1为雷达天线处于状态2时,雷达天线与转塔的重力使转塔产生的变形角度;θ2为雷达天线处于状态3时,雷达天线与转塔的重力使转塔产生的变形角度;x1、x2和x3分别为状态2、状态3和状态1时雷达天线质心在坐标系中的横坐标。
将式(10)按照式(9)化简得:
雷达天线处于不同状态时转塔系统的物理关系如图5所示,由此可得:

图5 转塔系统物理关系
式中:A为雷达天线俯仰轴与转塔回转中心的距离,A=2 930 mm;λ1为雷达天线状态2的实际俯仰角度;λ2为雷达天线状态3的实际俯仰角度。由于俯仰控制系统存在一定的误差,所以理论俯仰角度与实际俯仰角度有一定的误差。
在雷达车体调平后,调平系统的误差可以忽略不计,在转塔基准面上通过合像水平仪测量未安装雷达天线时的角度β。安装雷达天线后,使用激光跟踪仪测量雷达天线在理论俯仰角50◦和70◦时的俯仰角数据σ,同时记录俯仰角度编码器的读数(即实际俯仰角λ),激光跟踪仪的读数与角度编码器读数之差即为系统变形角度θ= (σ-λ)×3 600。不计转塔重力的变形角度α=θ-β。测量记录如表1所示。

表1 测量记录表
将式(11)与式(12)联立方程组,经Matlab软件计算得到两组解,其中一组无意义,保留有意义的一组结果,即:x1=1 247.98,x2=2 012.07,x3=313.79。通过这种方法得到的雷达天线质心位置与俯仰轴的距离为A-x3=2 616.21 mm。
3 雷达天线质心位置验证
受测量工具和场地的限制,该型号雷达不能直接对实物进行质心测量,因此将上节的计算结果与理论计算结果进行比较。理论计算一般是在三维模型软件中直接对各组成部分设置密度,由软件计算得到装配体的质心位置。该型号雷达天线组成复杂,计算量很大,因此该方法不适用。理论计算另一种方法是利用力矩平衡方程进行求解。已知装配体各组成部分的质心位置和重量以及装配体的总重量,列方程即可求得装配体的质心位置:
式中:f为雷达天线的重力;l为雷达天线质心相对于原点的位置;f1,f2,···,fn为各组成部分的重力;l1,l2,···,ln为各组成部分质心相对于原点的位置。
采用式(13)的计算方法求得雷达天线质心相对于俯仰轴的距离为2 665 mm,与上节计算结果相差1.83%。
4 结束语
本文以某雷达车转塔系统为基础,借助挠曲线近似微分方程建立数学模型,将测量结果代入数学模型,通过软件计算求得该型雷达天线的质心位置,与理论计算结果对比,结果相近。该方法的优势在于:1)不受限于场地和测量仪器,也不需要进行繁多的数据收集和复杂的理论计算;2)在产品初样阶段能够较为准确地估算出实际工况下的雷达天线质心位置;3)该方法是对理论计算的验证,在整车的质心估算中,可用来修正理论计算结果。
在结构满足挠曲线近似微分方程使用条件的前提下,本文提出的雷达天线质心位置估算方法效率高、结果准确可靠,可为相关车载雷达天线或相似结构产品的质心位置估算提供工程应用参考。
