微波滤波器的装调融合建模与反演*
2024-03-30杜志强周金柱林强强董晓冬
杜志强,刘 法,周金柱,林强强,董晓冬
(1.西安电子科技大学高性能电子装备机电集成制造全国重点实验室,陕西 西安 710071;2.中国电子科技集团公司第十研究所,四川 成都 610036)
引 言
微波滤波器是通信系统中重要的选频装置,用于抑制干扰信号和谐波信号。对滤波器而言,设计和制造是关键步骤。目前,滤波器设计理论已经基本成熟,但制造阶段存在很多问题。由于制造精度低、装配误差等原因,直接制造出的滤波器通常不满足电性能要求,因此,在设计阶段会加入调谐元件,通过调试调谐元件弥补制造阶段产生的误差。
为了弥补误差,往往需要对滤波器的调谐元件进行人工调试,使滤波器满足设计指标。人工调试LC滤波器(电感电容滤波器)的过程,实际上是对电感这一调谐元件的优化过程。大多数情况下,整个调试过程伴随着多次试错,不仅耗费时间,而且多次装调会对滤波器电感的焊点造成损伤,从而导致LC滤波器报废,因此实现LC滤波器的有效演进与快速智能装调具有重要意义。另外,滤波器的设计、制造阶段信息不互通,数据割裂,当滤波器出现问题时,制造到设计的故障反馈响应周期长,而且设计制造周期的数据无法得到有效利用。这些因素降低了滤波器设计制造迭代效率,导致滤波器设计制造周期过长。随着通信产业的快速发展,对微波滤波器设计制造周期的要求也越来越高。
设计制造周期的流程以及经验数据是研发周期知识的重要组成部分。当研发周期结束后,应对相关设计制造周期数据进行进一步的整理,建立相关数据库,实现设计制造周期数据的关联、互通和利用。目前,为了解决数据规范化存储的问题,知识图谱技术被广泛应用于信息智能搜索领域[1]。通过关键词匹配技术进行知识库匹配能够快速获取用户所需知识,通过建立知识图谱数据库能够实现数据关联以及数据的有效管理和利用,缩短产品的设计制造周期,提高设计制造周期迭代效率,增强设计与制造的协同。
随着数据方法的发展,许多数理统计方法在工程中得到应用。这些方法能够充分利用设计制造周期的数据,避免物理模型依赖,并且计算速度快、适用于具有非线性映射关系的问题,但是缺乏可解释性,而且过于依赖数据的质量。物理方法的可解释性强,不依赖数据可靠性且应用场景更加丰富。因此,将机理数据进行融合建模,能够实现数据方法与物理方法优缺点互补,既能够有效利用历史数据,又具有可解释性,该方法已经应用于多个领域[2]。
本文提出了一种微波滤波器装调融合建模与反演方法,利用知识图谱将微波滤波器的数据与机理进行规范化存储,利用机理数据融合建模的方法构建微波滤波器正向演进模型,基于正向演进模型,结合渐进空间映射算法,构建微波滤波器快速装调反演模型,从而实现微波滤波器的性能演进与装调反演。演进与反演实验验证了该方法的有效性。
1 知识图谱构建
知识图谱的构建可分为自顶向下(Top-down)和自底向上(Bottom-up)两种方式。自顶向下的方法先构建本体,然后根据本体进行实体和关系的抽取;自底向上的方法先进行实体和关系的抽取,然后根据抽取结果归纳聚类,抽象出本体[3]。LC滤波器的设计制造周期数据主要来自滤波器的设计文档、制造过程记录以及诊断维护记录,通常为明确的微波领域专业知识,因此本文使用自顶向下的方式构建知识图谱。构建本体包括规定实体类型、规定关系类型和规定关系类型的头尾实体类型,从而为知识三元组提供规范。
为了实现微波滤波器设计制造周期数据的相互关联,首先将设计制造周期数据分为设计数据、制造数据、诊断记录、调测数据以及基于机理数据计算出的结果。通过关系将头尾实体连为一对三元组,一对知识三元组是一对相互关联的数据,机理数据融合建模流程如图1所示。

图1 机理数据融合建模流程
实体类型包括滤波器、理想中心频率、理想带宽、理想插入损耗、理想回波损耗、理想带外抑制、阶数、耦合方式、生产日期、形状尺寸、理想耦合系数、设计师、电容、电感、调测编号、调谐元件物理尺寸、散射参数、中心频率、带宽、插入损耗、回波损耗、带外抑制、故障描述、元件调整量、耦合系数、故障位号、预测耦合系数和预测散射参数。关系类型包括设计信息、制造信息、故障信息、调测信息、性能、解决方案、计算方法和预测。头尾实体和关系类型三元组如表1所示。计算方法为机理公式,〈头实体,计算方法,尾实体〉三元组的含义为:头实体通过机理公式计算得到相应的尾实体。

表1 头尾实体和关系类型三元组
微波滤波器知识图谱本体构建的节点结构如图2所示。读取相应的结构化文件就可以得到微波滤波器的知识图谱,从而实现数据关联、有效管理以及可视化表征。
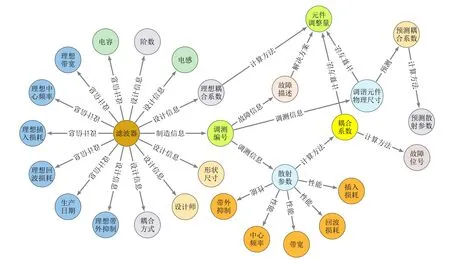
图2 微波滤波器知识图谱本体构建
2 融合演进
为了挖掘更多的有效信息,本文利用机理数据融合建模的方法构建微波滤波器正向演进模型,实现LC滤波器由调谐元件物理尺寸到电性能的演进。
2.1 构建演进模型
根据微波滤波器的阶数、中心频率、带宽和回波损耗,通过滤波函数能够得到理想散射参数,代入下文所述的耦合矩阵提取方法,可以得到滤波器的理想耦合矩阵M0,通过仿真设计软件优化得到理想元件物理尺寸x0。实际调谐元件物理尺寸为xf时,相应的耦合矩阵为M,此时LC滤波器的电性能不能满足设计指标。设存在映射关系:M=F(xf)[4]。
根据滤波器的耦合矩阵综合理论[5],滤波器的广义耦合矩阵一般表示为:
式中:mij=mji,非零元素mij表示谐振器i和谐振器j之间的耦合系数;mii表示谐振器i的自耦合系数;下标S表示源,下标L表示输出负载,mSj表示源与谐振器j之间的耦合系数,mLj表示输出负载与谐振器j之间的耦合系数。
通过耦合矩阵能够计算出散射参数响应[5],耦合矩阵M与滤波器的电性能之间存在如下关系:
式中:S21(f)和S11(f)分别表示滤波器的传输系数和反射系数,它们是滤波器频率f的函数;M表示耦合矩阵;I是单位矩阵;W表示滤波器的带宽;f0表示滤波器的中心频率;在阻抗矩阵R中,除了R11=R1,其他元素均为0,Qi表示第i个腔体的无载品质因数,R1和R2分别为源阻抗和负载阻抗。
通过神经网络模型与滤波器机理公式的结合构建LC滤波器电性能的融合演进模型,模型如图3所示。
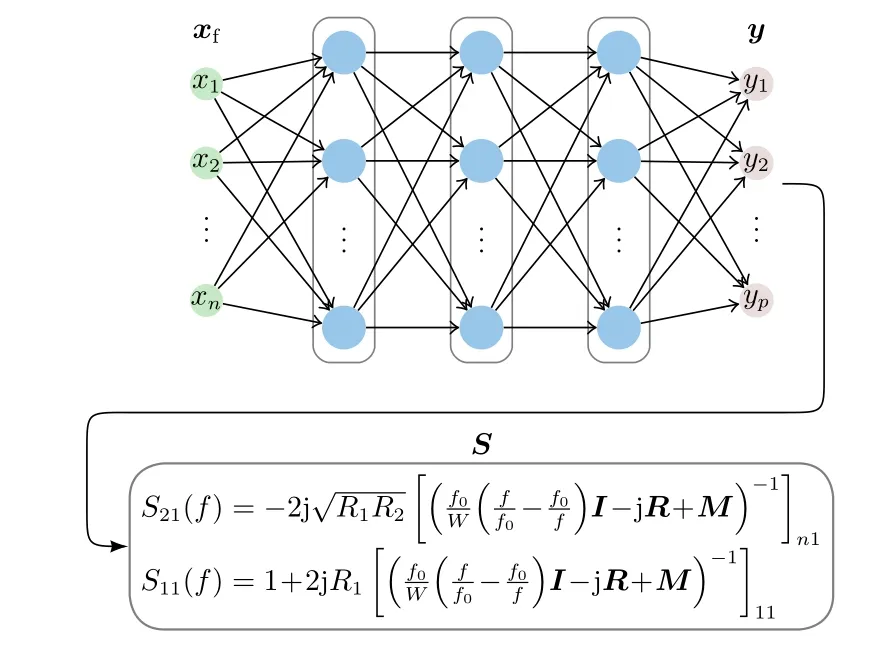
图3 演进模型示意图
该模型将神经网络与机理进行连接,神经网络建立LC滤波器电感长度xf= [x1,···,xn]与该电感长度对应耦合系数y= [y1,···,yp]的映射,根据输入电感长度与输出耦合系数建立反向传播(Back Propagation, BP)神经网络结构,根据输入电感长度的个数和输出耦合系数的个数以及样本个数合理设定隐藏层节点个数。按照误差BP算法训练多层前馈神经网络,训练过程分为两个步骤:1)数据正向传播,从输入层开始传递,经过隐藏层最终到达输出层,并计算误差;2)误差反向传播,从输出层开始传递,经过隐藏层最终到达输入层,根据链式法则依次调节每两层之间的权重和偏置,从而最终确定神经网络的权重和偏置。最后将未经训练的数据集输入到神经网络中,得到预测输出,判断预测输出与实际输出的误差,从而判断该神经网络的有效性。最后,由该预测耦合系数组成的耦合矩阵通过公式(2)得到预测电性能S。
为了获取用于神经网络训练的电感长度和散射参数训练集,本文通过实验对LC滤波器的电感进行了100次随机调试,使用3D激光轮廓仪和矢量网络分析仪分别采集每次调试后的电感长度和散射参数,生成100组数据。为了获取耦合系数,本文采用基于模型的矢量拟合法进行参数提取。文献[6]提出了一种简单有效的方法,通过矢量拟合从S参数数据中移除端口与传输线带来的相位加载效应,将移除相位加载效应后的S参数转换为导纳参数Y,使用有理函数近似的方法提取耦合系数。具体方法是增加多个额外的极点与零点,拟合反射参数S11和S22。在复平面中,大部分零点与极点都集中在原点周围,少数远离原点。谐振器对谐振频率附近的电性能有显著影响,远处的零点与极点是传输线和负载影响的结果,将远处的零点与极点移除实现相位加载效应的移除[7]。移除相位加载的结果如图4所示,随着频率远离坐标原点,相位趋于0,移除了端口与传输线对相位的影响,相位加载效应得到明显改善。改善后散射参数S11和S22的零点与极点如表2所示,零点与极点均在复平面原点附近。
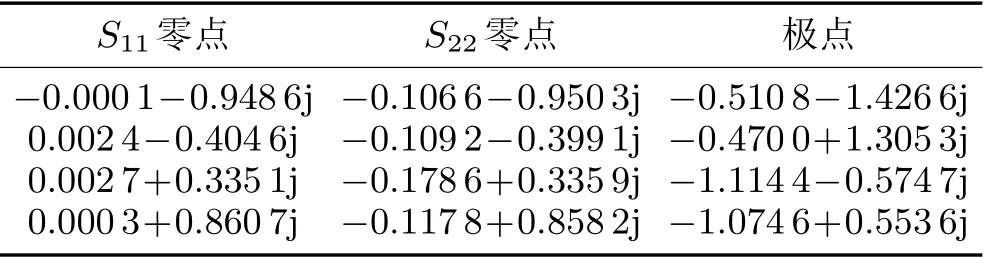
表2 改善后散射参数的零点与极点

图4 移除相位加载前后对比
将移除相位加载的S参数转换为Y参数,可使用矢量拟合算法拟合Y参数。根据Y参数求解有理函数的极点和留数,根据耦合矩阵综合理论[5]求解耦合系数,由耦合系数组成耦合矩阵。求解方程如下:
式中:K∞是与有限传输零点个数有关的因子;λk为导纳参数的极点;s=jω,ω为频率;r11k,r12k,r21k和r22k分别为对应导纳参数的留数;N表示滤波器的阶数。
通过耦合矩阵旋转方法[5],得到符合LC滤波器拓扑结构的耦合矩阵。
提取的耦合矩阵如图5所示。为了验证耦合矩阵提取方法的准确性,将提取耦合矩阵对应的S参数与原始S参数进行对比,如图6所示,提取耦合矩阵对应的S参数能够完全拟合原始S参数。
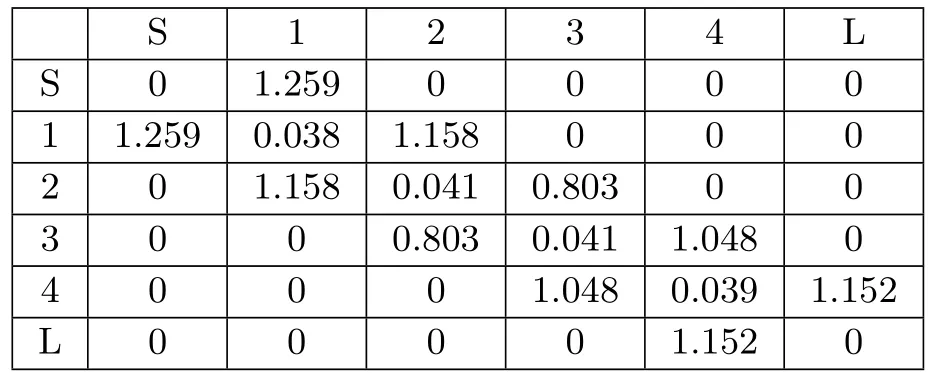
图5 提取的耦合矩阵

图6 提取耦合矩阵对应的S 参数
2.2 实验验证
本文实验所用的LC滤波器实物如图7所示,设计指标如下:

图7 LC滤波器
1)中心频率为118 MHz;
2)带宽为20 MHz;
3)插入损耗<2 dB;
4)回波损耗>25 dB;
5)在偏离中心频率30 MHz以外,抑制>30 dB。
通过建立前馈神经网络,进行LC滤波器电性能预测。该网络包含1个输入层、3个隐藏层和1个输出层[8–9]。输入层包含4个节点,对应于输入电感长度的4个特征。每个隐藏层都包含8个节点,分别使用ReLU、Sigmoid和Tanh作为隐藏层的激活函数,从而引入非线性变换。输出层包含9个节点,对应于输出耦合系数的9个特征。通过BP算法和Adam优化器进行训练,网络根据训练数据中输入和输出之间的差异来调整权重和偏置,以最小化损失函数(即均方误差)。通过5 000次迭代训练,均方误差降为2.030 6E-5。该BP神经网络具体参数如表3所示。

表3 BP神经网络参数
对演进预测能力进行验证,测试集合的电感长度输入如表4所示,该神经网络的预测耦合系数输出如表5所示。3组电感长度的测试结果如图8所示。
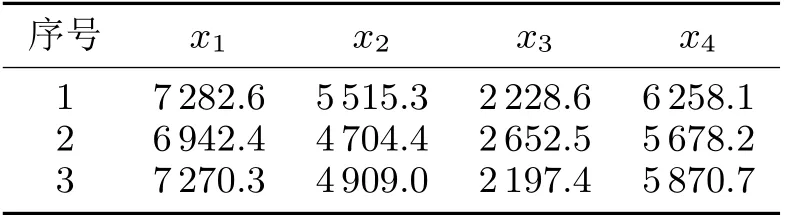
表4 测试集合电感长度

表5 预测耦合系数

图8 电感长度测试结果
通过公式(2)得到耦合矩阵对应的散射参数响应,最终演进的3组电性能与实测电性能对比如图9所示,散射参数曲线基本重合,具备良好的预测效果。

图9 预测电性能与实际电性能对比
该性能演进过程的知识图谱示意图如图10所示。

图10 性能演进知识图谱示意图
3 装调反演
3.1 电感长度对耦合系数的影响
为了研究LC滤波器调谐元件即电感对滤波器耦合系数的影响,本文通过调试电感改变其物理长度,得到相应电性能对应的耦合系数。如图11所示,通过改变1号电感的电感长度,得到耦合系数m11,m22,m33和m44的变化趋势。

图11 耦合系数和电感长度变化关系
由图11可知,改变调谐元件物理尺寸可以改变耦合系数,从而改变滤波器的电性能。随着1号电感物理长度的增加,对应耦合系数m11呈减小趋势,并且电感长度与耦合系数m11的函数关系近似于线性关系。非相关耦合系数m22,m33和m44基本保持不变,不受1号电感长度变化的影响。由此可知,LC滤波器上的每一个电感与耦合矩阵中对应元素即耦合系数一一对应,电感物理长度的变化会导致对应耦合系数的变化,且二者之间的函数关系近似于线性关系,因此建立耦合系数与电感长度之间的映射关系。调整调谐元件物理尺寸可以恢复滤波器的理想耦合系数,使得基于耦合系数的反演得以实现。
3.2 构建装调反演模型
首先使用上述神经网络模型得出理想耦合系数对应的物理尺寸,基于该物理尺寸对LC滤波器进行粗调,将该物理尺寸作为初始长度,利用渐进空间映射法对LC滤波器进行精调。
选定LC滤波器出厂时的电感长度作为上述神经网络模型梯度优化的初始值,目标输出为理想耦合系数,以预测输出与目标输出的均方误差作为损失,根据链式法则求解损失对输入的梯度,对输入进行梯度优化迭代。学习率和迭代次数会影响模型的稳定性和精度,经过多次调整,确定学习率为0.01,迭代次数为30。将得到的优化后的电感初始长度作为渐进空间映射法的初始电感长度。
接着,基于渐进空间映射法对LC滤波器进行精调。渐进空间映射法选取一个速度更快的粗糙模型替代LC滤波器的电性能响应,该方法自提出以来,在微波领域得到了普遍应用[10–11]。“精细模型”为LC滤波器的全波模型,“粗糙模型”是通过耦合矩阵计算电性能响应。渐进空间映射法在LC滤波器调试中的应用流程如图12所示。

图12 渐进空间映射法应用流程
3.3 实验验证
搭建实验环境,实现电性能测试以及电感长度测试,实验环境如图13所示。

图13 测试仪器与设备
本文实验对象LC滤波器的理想电性能如图14所示。利用上文提取方法,该滤波器的耦合系数如图15所示。因此理想耦合系数= [1.222,1.130,0.822,1.130,1.222,0,0,0,0],通过上文神经网络的梯度优化求解得到初始电感长度= [7 018.4,4 339.4,2 388.2,5 734.8]。

图14 S 参数迭代变化

图15 LC滤波器理想耦合系数
由图11能够得到耦合系数随电感长度的变化率,微小的电感长度变化就能改变耦合系数。根据初始电感长度装调的滤波器已经具有良好的电性能,因此物理尺寸变化量a的取值不宜过大,否则会导致电性能迅速恶化,本文取a=-100和ε= 0.02,应用渐进空间映射法。迭代过程中电感长度的变化如图16所示,得到的电感长度迭代变化如表6所示,得到的耦合系数迭代变化如表7所示。

表6 迭代过程中电感长度变化
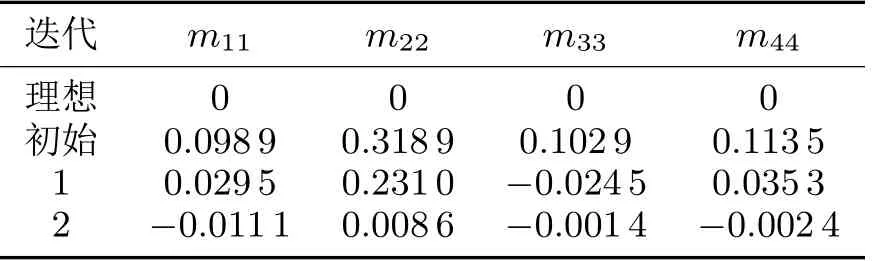
表7 迭代过程中耦合系数变化

图16 迭代过程电感长度的变化
由反演结果分析可知,通过神经网络梯度优化得到的初始电感长度所对应的散射参数已具备良好的电性能,再进行两次基于渐进空间映射法的调试便可获得非常接近理想性能的散射参数,能够实现LC滤波器的快速装调反演。相比于人工经验调试,该方法具有省时、省力的优势。反演过程的知识图谱示意见图17。

图17 反演知识图谱示意图
4 结束语
本文提出了一种微波滤波器装调融合建模与反演方法,根据微波滤波器设计制造周期数据与机理构建知识图谱;采用前馈神经网络与微波滤波器机理相结合的方式进行融合建模,对滤波器散射参数进行预测;基于正向演进模型,结合渐进空间映射算法,对微波滤波器进行迭代装调反演。实验结果表明:该方法能够实现LC滤波器设计制造数据的有效关联和管理,能够进行可视化表征;实现了LC滤波器性能演进的有效预测,预测散射参数与实际散射参数基本重合;通过两次装调便可实现LC滤波器故障性能的快速修复,相比于多次试错的人工调试,本文提出的装调方法具有省时、省力、可靠的优势。该方法适用于微波滤波器设计制造周期数据的有效管理,能够指导人工进行微波滤波器装调。将此方法应用于微波滤波器的自动化装调可以极大地解放劳动力。
