射频连接器装配位移的机电耦合建模及实验*

甘宇鹏，周金柱，赵博阳，樊国壮，高达林

（1.西安电子科技大学高性能电子装备机电集成制造全国重点实验室，陕西 西安 710071；2.西安电子科技大学杭州研究院，浙江 杭州 311231）

引 言

射频连接器是通信系统中重要的基础射频元件，用于射频设备中各个组件、天线单元、功分网络等不同射频模块的互连[1]。常用的射频连接器包括SMA，SMB，SMP等系列，不同的应用场景需要选用不同的射频连接器，以保证射频系统的可靠性。

随着射频系统向小型化方向发展，射频连接器也趋于小型化和密集化，SMP系列射频同轴连接器具有小型化、轻量化的特点，特别适合器件的模块化安装[2]。天线单元与发送/接收（Transmit/Receive,T/R）组件之间常常使用SMP射频连接器实现快速互连，以满足维修性与互换性的要求[3–4]，传统的人工安装方式难以满足实际需求。文献[5]研究了射频连接器的自动化装配，分析装配过程中阻力的影响，建立了压装力与连接器压装位移的关系。文献[6]研究了射频连接器的偏转对电性能的影响，设计了一种连接器盲插互联压接装配装置。文献[7]分析了温度对射频连接器性能的影响，得出温度对连接器插入损耗的影响关系。文献[8]研究了射频连接器退化的接触表面对回波损耗和插入损耗的影响机理，建立并分析了退化同轴连接器的高频等效模型。文献[9]研究了射频连接器接触表面不同恶化情况下的信号干扰，并提出了一种非线性电路模型，阐述了非线性干扰信号和接触表面恶化程度的关系，并依据电路模型计算出接触表面两部分的非线性干扰信号。

对于现代化的自动装配过程，射频连接器的装配位移偏差对电性能的影响规律尚缺乏研究，自动化设备无法根据产品的电性能指标控制机器手安装射频连接器。

本文基于微波网络理论建立射频连接器装配位移影响的互连射频连接器模型。将一对互连射频连接器划分为不同的微波网络，将接触区域的电路模型等效为接触阻抗，单个射频连接器等效为同轴传输线，简化了计算过程，同时使得建立的互连射频连接器模型具有通用性。

1 装配位移的机电耦合建模

1.1 射频连接器微波网络构建

相控阵模块连接结构如图1所示，功分网络每路出口焊接一个SMP阳极连接器，中间是一个SMP双阴极连接器，底座每路焊接一个SMP阳极连接器。现代的自动化装配过程通常是由机械臂控制功分网络或底座来对齐定位板，同时完成多个射频连接器的装配。射频连接器的装配位移对其传输电性能有很大的影响，要使机械臂安装的每个射频连接器的装配位移都满足电性能要求，就需要建立装配位移与电性能的关系，以指导机械臂工作。

图1 相控阵模块连接结构图

图2为一对射频连接器连接示意图。取其中一路连接器进行研究，固定下方阳极连接器并与双阴极连接器保持完全连接，即可将其等效为一个阴极连接器。将整体视作一对射频连接器，上方是阳极连接器，下方是阴极连接器，最大装配位移（连接器阳极插针长度）见图2。连接器阳极插针插入连接器阴极插孔的深度就是装配位移。

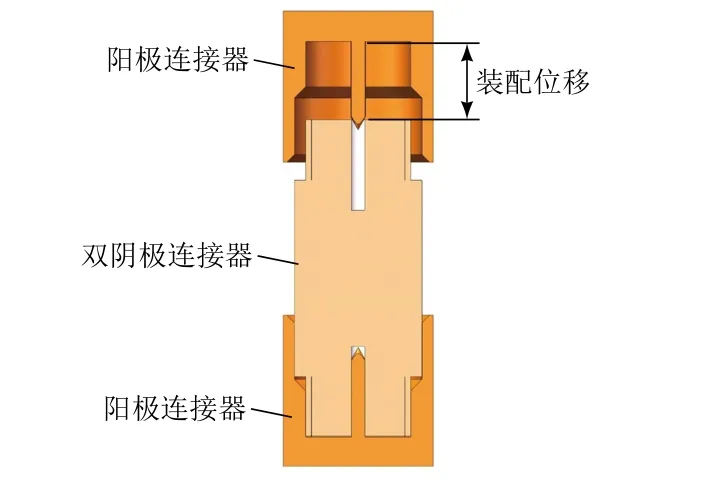
图2 一对射频连接器连接示意图

基于微波网络理论将不同装配位移的一对互连射频连接器分为阳极射频连接器（包含插针）、接触区域和阴极射频连接器（包含插孔）3个部分，如图3所示。每一部分看作一个二端口网络，因此不同接触状态的射频连接器可以看作3个二端口网络级联后组成的二端口网络[10]。端口1为输入端口，端口2为输出端口。

图3 互连射频连接器微波网络结构图

射频连接器接触区域如图4所示，接触区域是指阳极连接器插针与阴极连接器插孔相互接触的部分，电信号经过接触区域时会有一定的损耗，因此可将接触区域视作一个阻抗Zc。当互连射频连接器装配位移发生变化时，其插针与插孔的接触面积也会线性变化，即接触区域的等效阻抗Zc发生变化。

图4 射频连接器接触区域

射频连接器装配位移x与接触区域的等效阻抗Zc的关系可以近似为一个二次多项式关系，具体推导见2.2节。根据二端口网络传输矩阵的定义，将接触区域视作一个阻抗，其传输矩阵可表示为[11]：

式中，a1，a2和c为多项式系数。互连射频连接器的阴、阳极连接器主要由内导体、填充介质和外导体组成[12]，内导体传输信号。阴极连接器的内导体为插孔，阳极连接器的内导体为插针。射频连接器的结构为同轴结构，因此阴、阳极连接器可以等效简化为两个同轴传输线。再根据二端口网络传输矩阵的定义，对于第i个同轴传输线，其传输矩阵为：

式中：γi和li分别表示第i个同轴传输线的传播常数和长度，传播常数可由同轴传输线的电路元件计算得出；Z0为特征阻抗。电路元器件参数与同轴线参数的关系如表1所示，表中：a为同轴线内导体半径；b为同轴线外导体内径；µ为介质层的磁导率；ε′为介质层介电常数的实部；ε′′为介质层介电常数的虚部；Rs为内导体表面电阻率；ω为输入电信号角速度。

表1 电路元器件参数与同轴线参数的关系

根据互连射频连接器微波网络结构，构建装配位移影响的射频连接器模型：

式中：A(x)为互连射频连接器的传输矩阵；A1为阳极连接器的传输矩阵；A2为阴极连接器的传输矩阵。

1.2 接触阻抗与散射参数关系推理

阳极射频连接器、接触区域和阴极射频连接器的传输矩阵级联后得到互连射频连接器模型参数：

根据散射参数与传输参数转换关系可得级联后的散射参数矩阵Sc：

化简式（5）可以发现连接器阴极和阳极存在一定关系，并且可以消去中间的连接器尺寸关系，进一步构建接触区域阻抗Zc和一对互连射频连接器散射参数的关系（式（6）），从而建立接触区域影响下的互连射频连接器机电耦合模型。

2 装配位移与接触阻抗关系

2.1 射频连接器实验平台

为了探究不同接触状态下的射频连接器电性能，设计并制作了射频连接器实验平台，平台三维模型如图5所示。

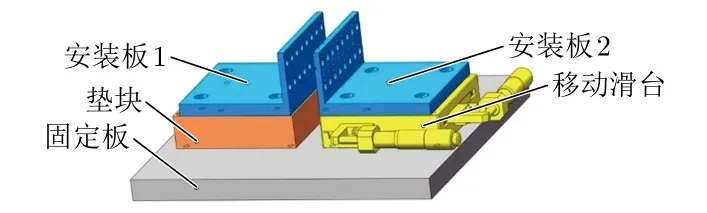
图5 射频连接器实验平台三维模型

射频连接器实验平台由两个安装板、垫块、移动滑台和底部固定板组成。安装板1和安装板2分别用于安装阴极射频连接器和阳极射频连接器；安装板1固定在垫块上，安装板2固定在移动滑台上；安装板1、安装板2、垫块和移动滑台整体安装在底部固定板上。

垫块与移动滑台具有相同尺寸，从而保证在实验过程中，只存在射频连接器移动方向的变化，其余实验条件不变。移动滑台上安装有高精度数显螺旋测微仪，方便显示射频连接器的接触深度。

2.2 装配位移与接触阻抗关系拟合

实验装置和一对测试的互连射频连接器如图6所示。左边测试样件为SMA阴极–SMP阴极射频连接器，右边测试样件为SMP阳极–SMA阴极射频连接器。将左边射频连接器的SMP阴极和右边射频连接器的SMP阳极对插连接。

图6 实验装置和一对测试的互连射频连接器

实验装置包括移动平台、矢量网络分析仪和实验平台。将两个待测射频连接器固定在平台的安装板上，并通过射频电缆连接至校准好的矢量网络分析仪，分别测试不同装配位移下互连射频连接器以及单个射频连接器的散射参数。

互连射频连接器测试过程中不同的装配位移如图7所示。图7（a）表示装配位移0 mm，接触状态为两个射频连接器刚刚接触；图7（b）表示装配位移1.5 mm，接触状态为两个射频连接器部分接触；图7（c）表示装配位移2.1 mm，接触状态为两个射频连接器完全接触。

图7 不同装配位移的射频连接器

不同装配位移连接器电性能测试结果如图8所示。当装配位移为2.1 mm 时，回波损耗(S11)在-23 dB以下，频段内最多反射了7%的信号，插入损耗（S21）接近0 dB，传输的信号接近百分之百。当装配位移为1.5 mm时，回波损耗（S11）约为-1 dB，频段内反射的信号约为89%，插入损耗（S21）约为-20 dB，传输的信号约为10%。由测试结果可以看出，随着装配位移的减小，射频连接器的电性能趋于恶化。在整个频段内，随着装配位移的减小，射频连接器电性能表现为回波损耗（S11）增大，连接器端口阻抗不匹配，信号发生反射，插入损耗（S21）减小，信号反射增多，传输信号减小。

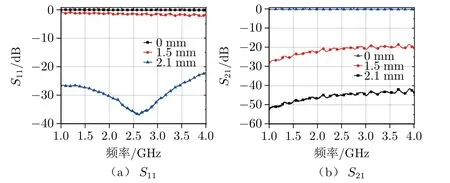
图8 不同装配位移连接器电性能测试结果

实验测得不同装配位移连接器的电性能后，由式（6）计算出相应的接触区域阻抗Zc，如图9所示。从图9可以看出，随着装配位移的减小，连接器接触状态发生恶化，表现为接触区域阻抗增大。此外，在整个频段内，接触区域阻抗随着频率的增大而减小。

图9 不同接触状态下互连射频连接器接触区域阻抗

得到接触区域阻抗后，接着建立阻抗和装配位移的映射关系，即通过接触阻抗Zc反映射频连接器的装配位移。根据图9的计算结果，选取不同频点（1 GHz，2 GHz，3 GHz和4GHz）的接触阻抗及对应的接触深度，通过曲线拟合探究接触阻抗和装配位移的关系，拟合曲线如图10所示。

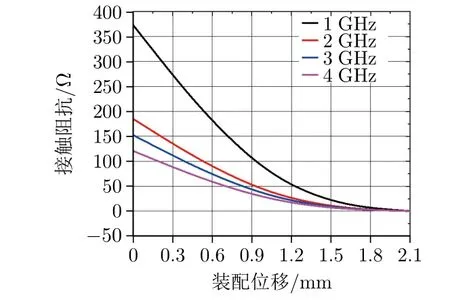
图10 接触阻抗和装配位移的拟合曲线

观察图10的关系拟合曲线发现，接触阻抗Zc和装配位移x的关系近似满足二次多项式关系。因此，定义互连射频连接器接触区域阻抗和装配位移的二次多项式关系为Zc=a1x2+a2x+c。3个待求系数a1，a2和c通过Python语言拟合计算得出。

将装配位移和接触阻抗的关系加入射频连接器互连的场路模型Acab中，可以得到装配位移下的机电模型。模型构建如下：

式中：上标1表示SMP阳极–SMA阴极连接器；上标2表示SMP阴极–SMA阴极连接器。

3 实验验证

基于互连射频连接器装配位移的机电模型，预测下一装配位移的射频连接器电性能，将传输矩阵A转化为散射参数。调节螺旋测微仪，使得射频连接器的阴阳极连接到下一装配位移，用矢量网络分析仪测出该位移下的散射参数，并与实验结果进行对比。图11为下一接触状态射频连接器电性能演进与实测对比。

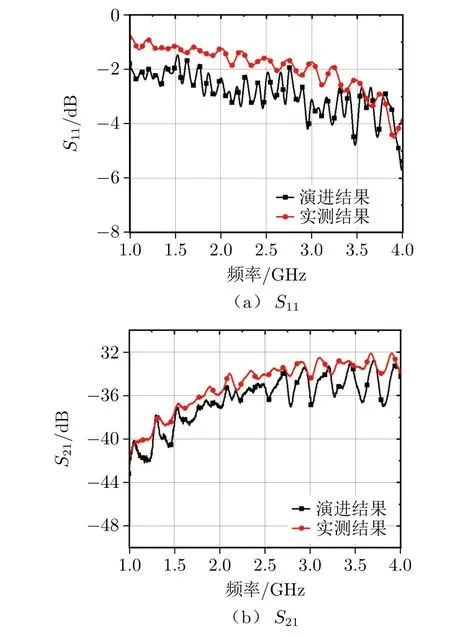
图11 下一接触状态射频连接器电性能演进与实测对比

由图11可见，当下一装配位移为1.3 mm时，互连射频连接器处于接触恶化状态。在整个频段内，演进结果和实测结果大体一致，回波损耗（S11）均在6 dB以上，插入损耗（S21）约为35 dB。局部频点差异较大的原因可能是在互连射频连接器场路耦合理论建模过程中，未考虑射频连接器的具体结构尺寸，将其等效为同轴传输线。而且实验中插针接触深度较小时，阴极和阳极射频连接器的接触状态易受外界环境因素干扰，导致实验数据噪声较大。

4 结束语

本文建立了射频连接器装配位移影响下的场路耦合模型，通过仿真验证和实验测试分析了射频连接器不同接触状态的影响，分析装配位移对接触区域阻抗的影响关系，并使用曲线拟合算法建立其数学表达式，实现射频连接器下一装配位移的反演。最后基于建立的场路耦合模型以及接触状态和接触区域阻抗拟合关系，建立射频连接器装配位移的机电耦合模型。通过搭建装配位移实验平台，验证了耦合模型的有效性。