考虑孔隙比的冻胀弱敏感性土修正PCHeave模型研究

贺佐跃

(1.广东省交通规划设计研究院集团股份有限公司，广东 广州 510507；2.中南大学 土木工程学院，湖南 长沙 410075)

冻胀弱敏感性土广泛应用于我国严寒地区的高速铁路(以下简称“高铁”)路基填料和机场填方等工程中,研究冻胀弱敏感性土的冻胀规律有助于这些工程的安全运营和管理[1-2]。土的冻胀敏感性分类是寒区路基设计的重要依据,叶阳升等[3]基于细粒含量对碎石类土、砂类土和细粒土进行了冻胀敏感性分类。SL 237—2019《土工试验规程》[4]规定粗粒质量百分比大于50%的土称为粗粒土,高铁路基A/B填料属于粗粒土,当B组填料细粒含量为5%～15%时为典型的弱冻胀敏感性土[1]。在分析冻胀弱敏感性土的冻胀问题时,现有文献往往忽略了土体密实情况对冻胀的影响。然而,王天亮等[5]在粗粒土的冻结试验中发现,细粒含量较低时干密度会对冻胀产生影响,试样的冻胀率随干密度的增大先增大再减小,根据叶阳升等[3]的研究成果,该粗粒土为冻胀弱敏感性土。干密度和孔隙比均能表征土体的密实情况,两者等价,本文将统一采用孔隙比表征。

非饱和土的冻胀与饱和渗透系数密切相关,饱和渗透系数越大,冻胀通常越显著[6-7],而饱和渗透系数通常受到孔隙比的影响。Laliberte等[8]通过Touchet粉质壤土、Columbia砂壤土和松砂等3种不同土样的渗透试验发现,土体的渗透性能与孔隙比有关,饱和渗透系数与孔隙比呈现出正相关性。Chapuis[9]统计分析了砂土孔隙比与饱和渗透系数之间理论关系的适用性,提出一套针对某一特定土体的理论计算选择方法[10-13]。然而,仅仅通过建立孔隙比与饱和渗透系数之间的关系,研究孔隙比对冻胀的影响规律是不够的。

孔隙比也会对未冻水含量产生影响,未冻水含量是研究冻胀模型的重要参数。Xu等[14]通过试验发现,随孔隙比变化,未冻水含量与温度之间的变化曲线彼此并不平行。当高于某一温度时,未冻水含量随孔隙比增大而减小,但减小幅度不明显;当低于某一温度时,未冻水含量随孔隙比增大而增大,但增大幅度也较小。未冻水含量随孔隙比变化的幅度在2%以内。目前,孔隙比对冻胀弱敏感性土的冻胀影响主要以试验研究为主[12-13]。实际上,PCHeave模型中与孔隙比直接相关的参数即为饱和渗透系数、饱和度和未冻水含量,这为基于该模型进行修正并研究孔隙比的影响提供了理论分析途径。

但现有文献尚未建立相关模型,理论系统地分析孔隙比对冻胀弱敏感性土的冻胀影响。首先本文分析孔隙比对冻胀弱敏感性土的饱和渗透系数、饱和度和未冻水含量的影响,然后将其导入到冻胀模型PCHeave[6-7]进行修正,并利用新模型分析孔隙比对冻胀弱敏感性土的冻胀影响并得出相应规律,最后通过试验验证新模型的有效性。

1 孔隙比对冻胀关键参数的影响

1.1 孔隙比对饱和渗透系数的影响

含水量、饱和度、饱和渗透系数和未冻水含量等土的自身因素,以及上覆压力、地下水位、冻结时间、降温速率和温度梯度等环境因素对冻胀弱敏感性土的冻胀有显著影响[15]。在这些因素中,除含水量及环境因素外,孔隙比对其他因素均能产生影响,研究这种影响关系对土的冻胀是很有必要的。

未冻结区,非饱和土的渗透系数与饱和渗透系数和饱和度有关[16-17],而土体的饱和渗透系数又与孔隙比e密切相关。现有文献提出了很多针对粗粒土饱和渗透系数的统计公式。针对松砂,Hazen方程[18]适用条件为:砂,松散(e≈emax),不均匀系数Cu≤5,有效粒径d10∈[0.1,3]mm,即级配曲线纵坐标为10%时所对应的粒径。当满足以上条件时,Hazen方程才可应用,若只满足部分条件或全不满足时,Hazen方程的准确性有待商榷。Kozeny[19]和Carman[20-24]基于大量试验,提出了Kozeny-Carman方程,但该方程参数较为复杂,且难以表征粗粒填料如砂土的饱和渗透性能。Taylor[25]把Kozeny-Carman方程简化为e3/(1+e)的线性函数,饱和渗透系数仅与孔隙比e相关。然而Chapuis[10]发现,即便是同种土,Kozeny-Carman方程的系数的取值也是不唯一的,并且大量试验发现,饱和渗透系数Ksat不仅与孔隙比e有关,对有效粒径d10也会产生影响。

( 1 )

需要说明,有效粒径d10的单位为mm,计算得到的饱和渗透系数单位为cm/s,式( 1 )等号两边量纲并不统一,但其是统计公式,并非理论公式,因此在计算时仍然是可以接受的。尽管由于土体参数测量的精度以及饱和渗透系数的试验操作流程等原因,式( 1 )的计算值与实测值之间存在一定误差,但大量数据统计结果表明,相对于其他考虑了孔隙比[26-30]的饱和渗透系数计算式,式( 1 )更接近粗粒土的实测值[9],在粗粒土中拟合效果非常好且应用广泛[10]。因此,本文将采用该方程来计算未冻结区的饱和渗透系数及其对冻胀弱敏感性土的冻胀影响。

式( 1 )中孔隙比对饱和渗透系数(lgKsat)的影响见图1。由图1可以看出,孔隙比会使饱和渗透系数发生很大变化,在整个孔隙比取值范围内,饱和渗透系数增加将近10倍,而饱和渗透系数是影响未冻结区水分迁移速率的重要参数之一,这说明孔隙比对冻胀弱敏感性土的冻胀也会产生较大影响。

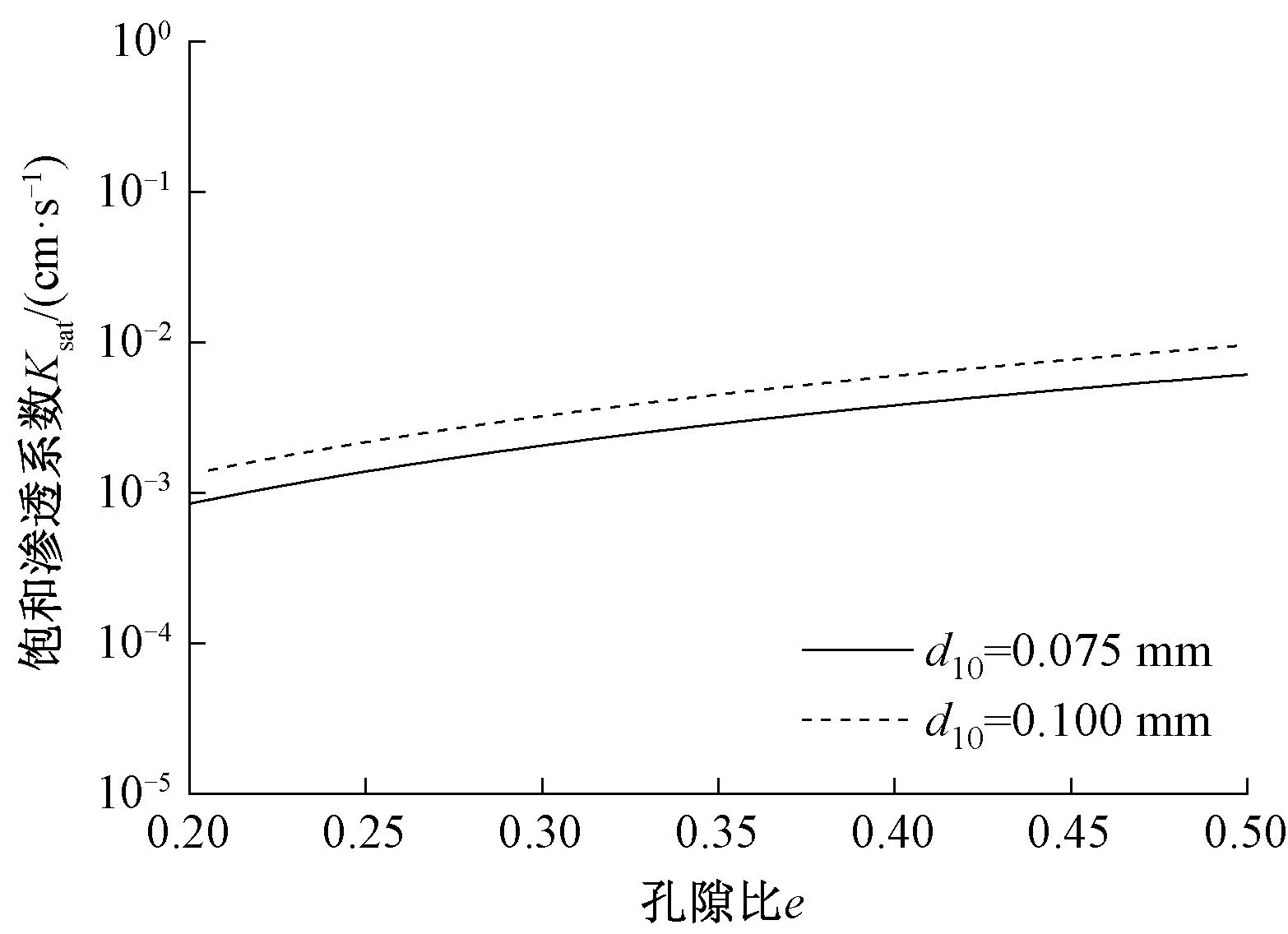
图1 孔隙比对饱和渗透系数的影响

1.2 孔隙比对未冻水含量的影响

冻胀弱敏感性土的未冻水含量很小,但冻胀弱敏感性土的冻胀对未冻水含量较为敏感,当未冻水含量少量增加时也能产生显著冻胀[15]。特别是-1 ℃未冻水含量对冻胀的影响显著,当-1 ℃未冻水含量较小时,几乎不产生冻胀;但当-1 ℃未冻水含量较大时,即使-1 ℃未冻水含量增加幅度很小,仍能产生显著冻胀。这说明未冻水含量对冻胀弱敏感性土的冻胀影响很大[15],有必要分析孔隙比对未冻水含量的影响。

Xu等[14]通过试验发现,当土体干密度在1.00 ～1.71 g/cm3变化时,若温度低于-2 ℃,未冻水含量随干密度增大而增大,若温度高于-2 ℃,情况相反,即未冻水含量随干密度增大而减小,试验结果见图2。产生这种现象的原因是干密度导致孔隙结构和大小发生变化。总的来说,尽管干密度对未冻水含量有影响,但这种影响幅度较小。由图2可以看出,温度为-0.5 ℃时的影响是最大的,但减小幅度仅约为2%,温度越大,减小或增加的幅度就越小。

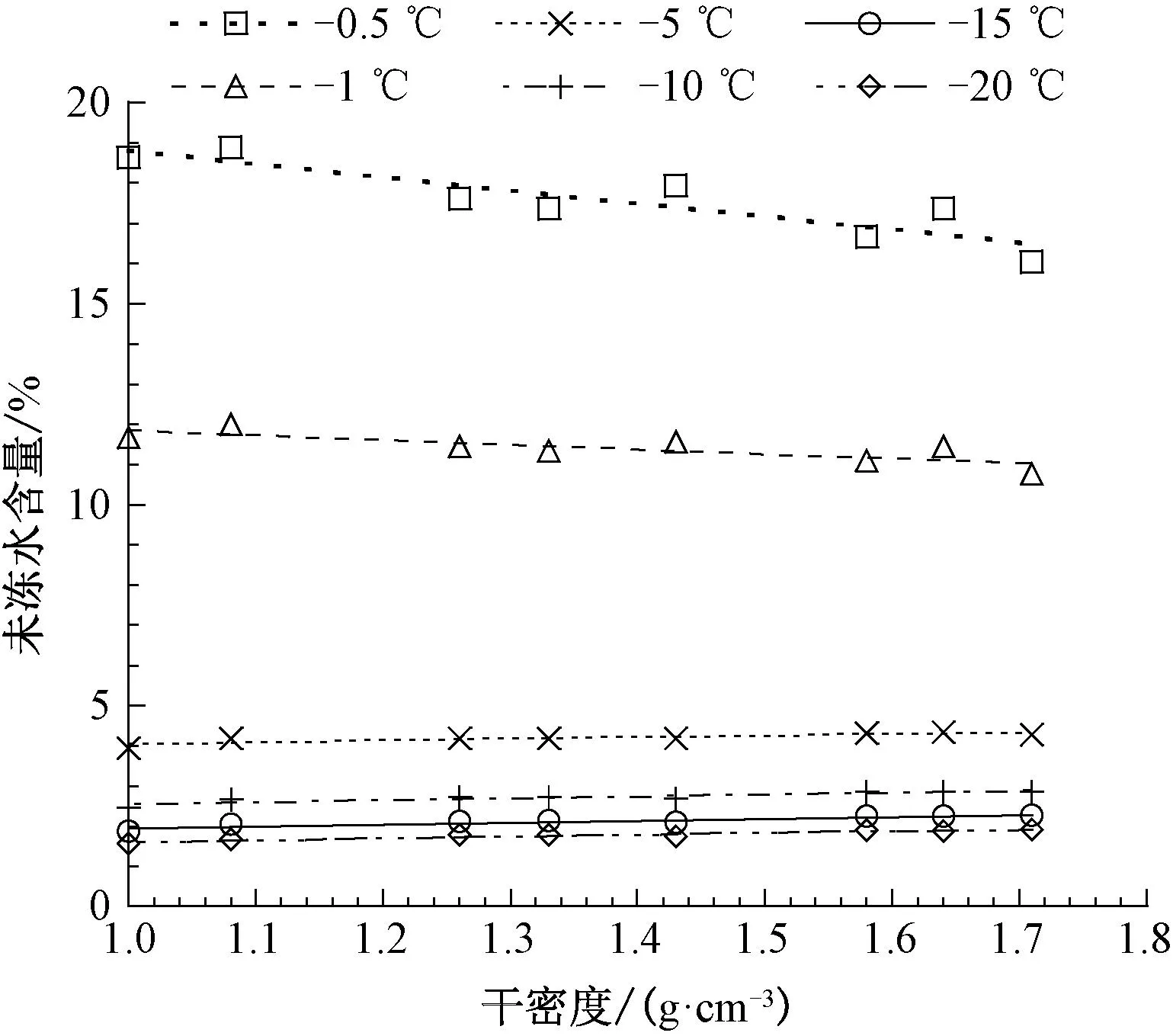
图2 干密度与未冻水含量之间的关系[14]

尽管这种变化幅度较小,但干密度对未冻水含量有影响这一结论是肯定的,而对冻胀弱敏感性土来说,未冻水含量的微小改变也能导致冻胀产生较大变化。本文对图2中的试验值进行拟合发现,干密度与未冻水含量之间存在很好的线性关系,拟合参数见表1。表1中,a为斜率;b为截距;R2为方差。由表1可知,温度较高时,斜率为负,代表未冻水含量随干密度递减;温度较低时,斜率为正,代表未冻水含量随干密度递增。

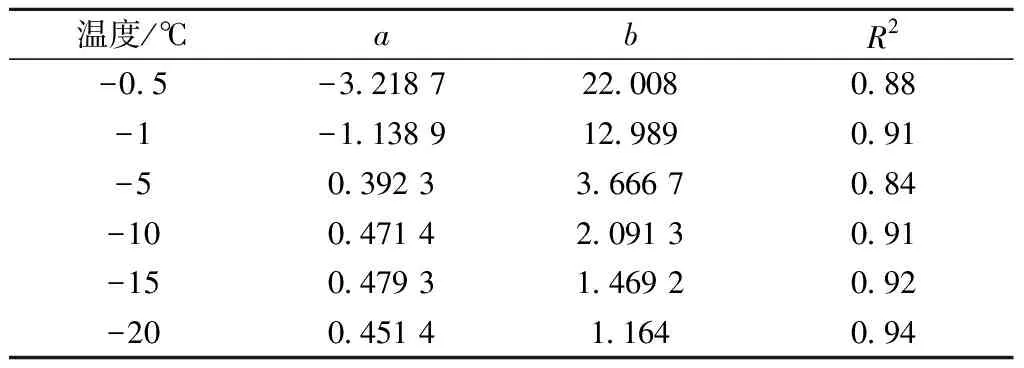
表1 干密度与未冻水含量的拟合参数

干密度与孔隙比具有等价关系,可表示为

( 2 )

式中:wu为未冻水含量;Gs为土粒比重。

2 修正PCHeave模型

冻胀实质上是热-质迁移的耦合过程,当低于冻结温度时,孔隙水会固化成冰,在水势梯度和温度梯度作用下,液态水从温度较高区域不断向冻结锋面迁移,促使冰透镜体不断萌生。判断冰透镜体萌生是研究的关键,Sheng等[6-7]认为冻结缘有效应力为0时(有效应力为总应力与中性应力之差,中性应力为孔隙水压与孔隙冰压的几何平均值),新的冰透镜体开始萌生,并建立了冻胀模型PCHeave。该模型已在工程实践中得到了很好验证,且已获得广泛认可。

但现有研究中的模型,包括PCHeave模型均不能模拟孔隙比对冻胀的影响,且孔隙比会影响土的饱和渗透系数、饱和度和未冻水含量,进而影响冻胀。在PCHeave模型中,当冻结锋面高于地下水位时,未冻结区的水分迁移速率服从达西定律,即

( 3 )

式中:vu为未冻结区的水分迁移速率,m/s;ρw为液态水密度;g为重力加速度,m/s2;xgw为地下水位,m;xf为冻结锋面位置,m;uw(xf)为xf处孔隙水压力;xgw为地下水位;ku为冻结锋面与地下水位之间未冻土的有效渗透系数,m/s,计算式为

( 4 )

其中,Sr为饱和度;n为孔隙率;I为体积含冰量;m为土体参数,默认值为9[15]。

把式( 1 )、式( 3 )导入到式( 4 ),即可得考虑孔隙比的未冻结区水分迁移速率vu为

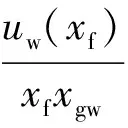
( 5 )

式中:A、B均为等于1的参数。

需要注意,式( 1 )单位为cm/s,而PCHeave中单位为m/s,因此vu需乘以系数0.01。此外,为避免式( 1 )中有效粒径d10带来的量纲不统一,本文将引进参数A、B,其中A的单位为m/s,B的单位为mm-1。

-1 ℃未冻水含量是PCHeave的重要参数之一[31-33],尽管尚未有孔隙比对-1 ℃未冻水含量的理论公式,但由第1节可知,孔隙比与-1 ℃未冻水含量之间可建立联系。将式( 2 )、式( 5 )导入到PCHeave框架内即构成了新的模型——修正PCHeave模型,利用新模型可分析孔隙比对冻胀弱敏感性土的冻胀影响。相较于原模型,修正PCHeave模型最显著的区别是可以考虑孔隙比的影响。

3 孔隙比对冻胀弱敏感性土的影响

本文将采用修正PCHeave用算例来研究孔隙比对冻胀弱敏感性土的冻胀影响。根据Sheng等[1]的研究,A/B料的细粒含量为7%,有效粒径为0.09 mm,土粒比重为2.7,初始质量含水量为5%;冻结时间为48 h,计算土柱高度为16 cm[4];地下水位位于土柱底部,初始孔隙比为0.2;导热系数为3 W/(m·K),顶端温度为-10 ℃,底端温度为10 ℃[1]。-1 ℃未冻水含量由式( 2 )得到。

孔隙比对冻胀弱敏感性土冻胀影响的计算结果见图3～图5。

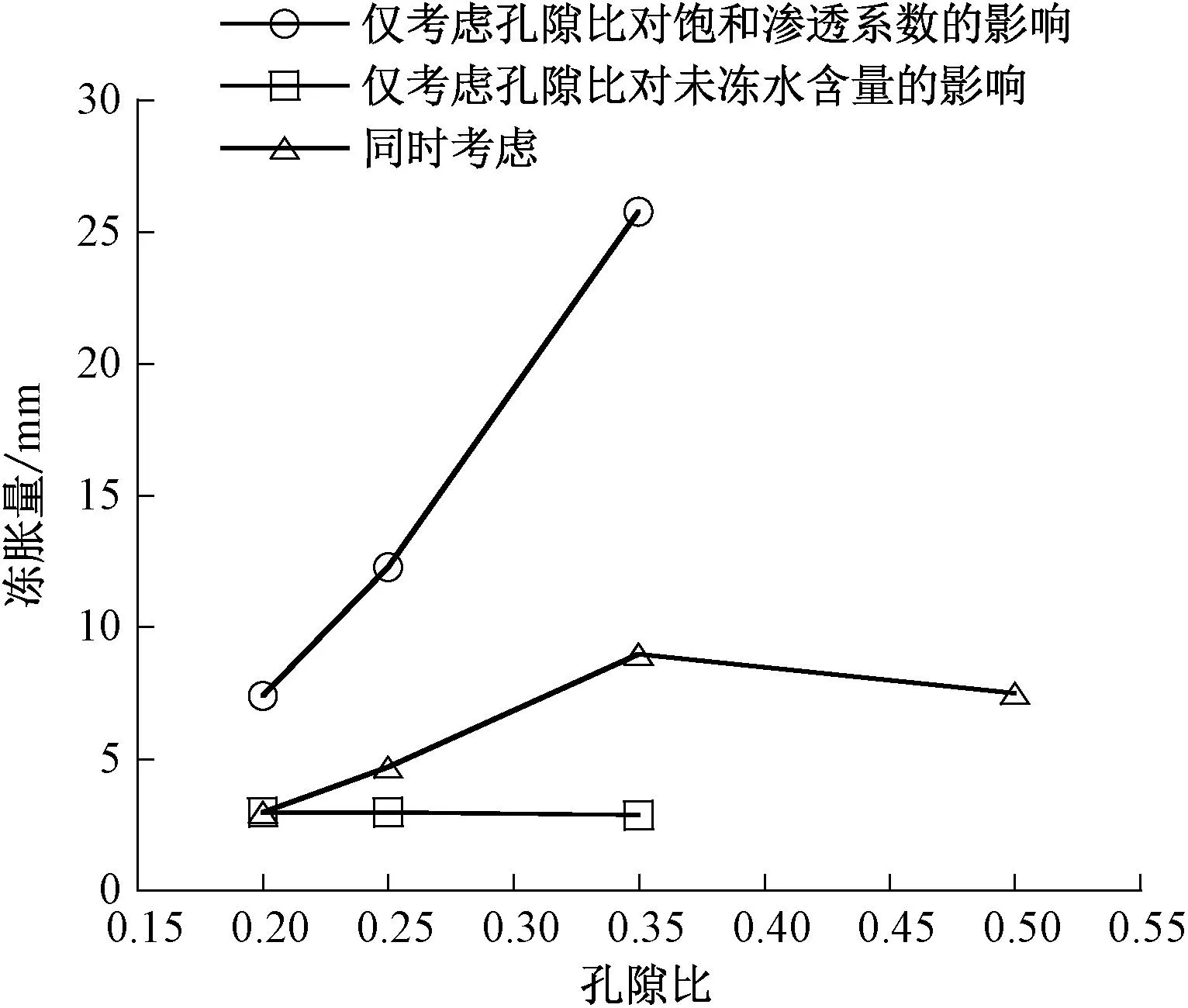
图3 孔隙比对粗粒土冻胀量的影响

由图3可以看出,同时考虑孔隙比对饱和渗透系数、未冻水含量的影响时,冻胀量随孔隙比先增大再减小。当孔隙比较小时,孔隙比增大导致饱和渗透系数增大,尽管此时-1 ℃未冻水含量有所减小,但由饱和渗透系数增大导致冻胀量增大的效应要大于由-1 ℃未冻水含量减小导致冻胀量减小的效应,宏观表现为冻胀量增大;当孔隙比较大时,-1 ℃未冻水含量随孔隙比增大而继续减小,此时由-1 ℃未冻水含量减小导致冻胀量减小的效应要大于由饱和渗透系数增大导致冻胀量增大的效应,宏观表现为冻胀量减小。这种变化意味着存在一个最不利孔隙比,使冻胀量达到最大值。

由图4可以看出,同时考虑孔隙比对饱和渗透系数、未冻水含量的影响时,冻结深度随孔隙比增大而逐渐增大,并不存在峰值,但增加幅度总体上仍然较小,最大、最小差值仅约为2.5 cm。由图5可以看出,孔隙比冻胀率的影响与图3具有类似趋势,即同时考虑孔隙比对饱和渗透系数、未冻水含量的影响时,冻胀率随孔隙比先增大再减小,存在一个最不利孔隙比使冻胀率达到最大值。

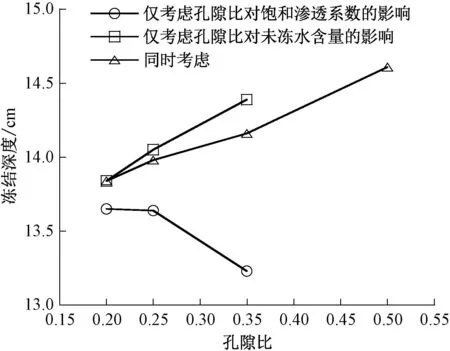
图4 孔隙比对粗粒土冻结深度的影响

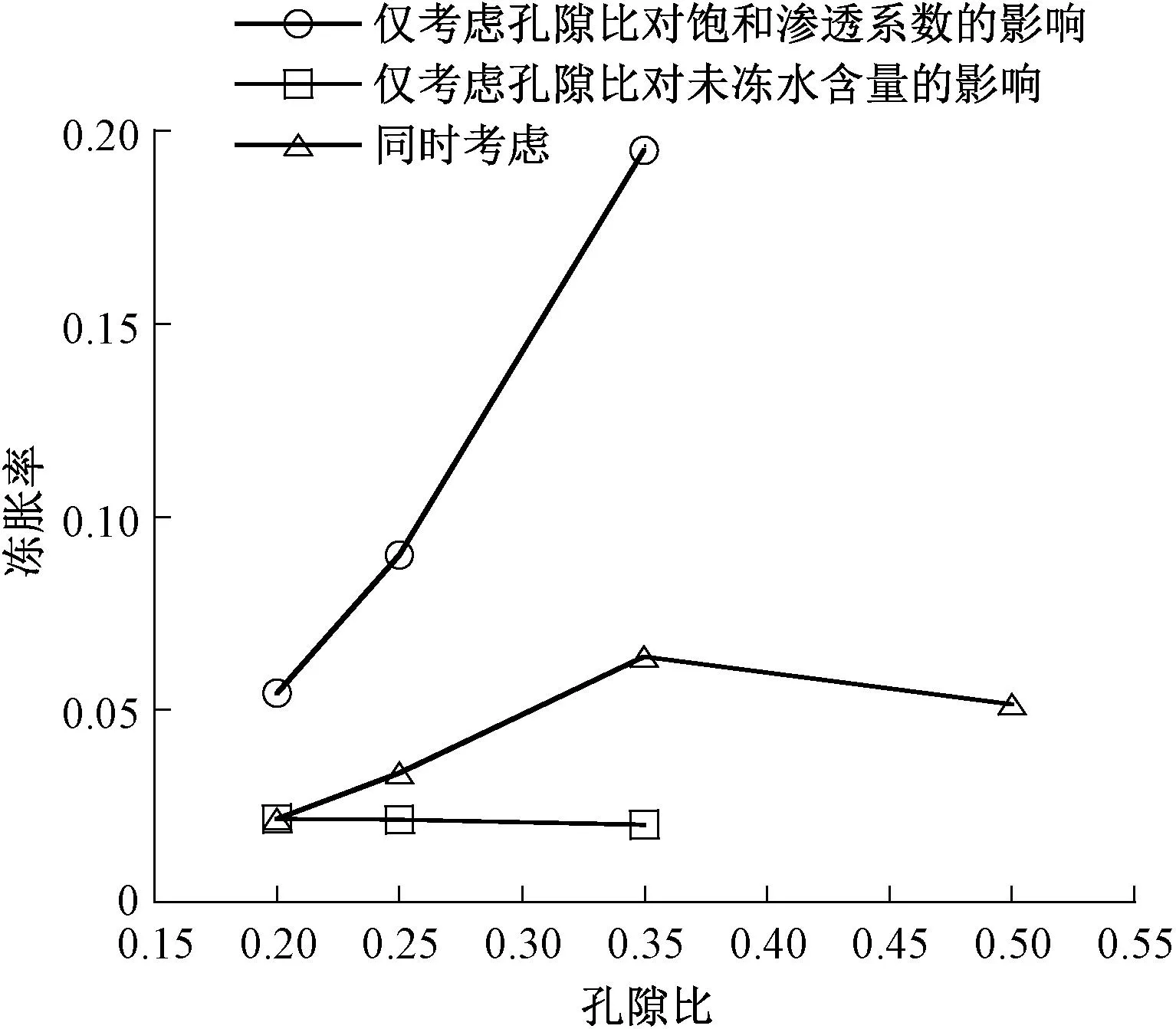
图5 孔隙比对粗粒土冻胀率的影响

此外,两个因素同时考虑时,冻结48 h后不同孔隙比下冰透镜体生成情况见图6。图6中,红虚线为冻结锋面;白色条状为冰透镜体。由图6可以看出,孔隙比越大,冰透镜体数量越多,分布也越均匀,但最厚冰透镜体与最大冻胀量时的孔隙比一致。

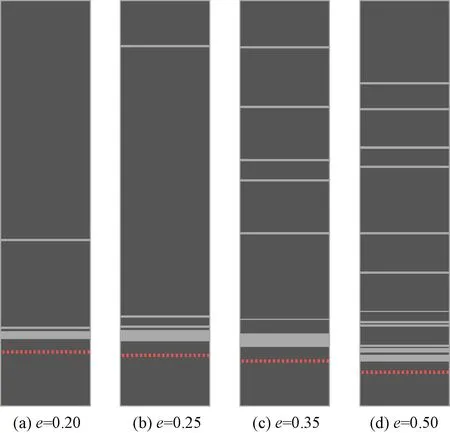
图6 48 h后不同孔隙比下冰透镜体生成情况(同时考虑)

然而,若仅考虑孔隙比对饱和渗透系数的影响,即假定未冻水含量不随孔隙比变化,此时冻胀量和冻胀率均随孔隙比显著增加,孔隙比为0.35时,冻胀量和冻胀率分别达到26 mm和0.19。这是因为孔隙比对未冻水含量的影响较大,饱和渗透系数的增加会显著提高未冻结区的水分迁移速率,导致冻胀量显著增加,而冻结深度随孔隙比逐渐减小。但这是不合理的,冻胀弱敏感性土的冻胀受到诸多因素的影响,不可能一直增加。若仅考虑孔隙比对未冻水含量的影响,除冻结深度略有增加外,冻胀量和冻胀率均减小,但减小幅度很小,这是因为孔隙比会降低未冻水含量,但这种降低幅度也是很小的。总的来说,同时考虑孔隙比对这两种参数影响的计算结果是居中的,也更合理。

冻胀弱敏感性土通常认为不能产生显著冻胀,但由图3可知,同时考虑孔隙比对饱和渗透系数和未冻水含量时,在一定孔隙比水平下也能产生较大冻胀。例如当孔隙比为0.35(孔隙率为0.26)时,冻胀量可达9 mm,此时饱和度仅为40.73%,即便是完全饱和,产生的原位冻胀也仅为3.4 mm。因此,必然有水分由地下水位不断迁移至冻结锋面,而传统冻胀理论认为冻胀弱敏感性土中细粒含量太少导致持水能力差,且在含水量较低时,土中液态水通常不连续,当最大冻结深度高于地下水位时,地下水难以迁移至冻结锋面。本文孔隙比对冻胀弱敏感性土的冻胀影响是以饱和渗透系数和未冻水含量为媒介产生的,孔隙比越大,饱和渗透系数越大,即使-1 ℃未冻水含量随孔隙比增大逐渐减小,计算得到的冻胀量也存在上升阶段。因此,若忽略孔隙比对粗粒土饱和渗透系数和未冻水含量的影响,就难以解释工程实践中冻胀弱敏感性填料产生的较大冻胀现象。

此外,式( 2 )中,参数a、b与土性有关,但现有研究中有关孔隙比对不同土体未冻水含量的影响的试验数据十分有限,在实际计算过程中,a、b具体取值存在一定困难,但Xu等[14]研究表明,孔隙比对未冻水含量的影响较小,影响幅度在2%以内,因此在给定温度下,可认为a、b取值一样。这种处理方式基于现有试验数据得出,具有一定的合理性,但对不同土性仍需进一步试验研究。

毫无疑问,冻胀弱敏感性土中的细粒含量对冻胀也会产生很大影响,但本文仅研究粗粒土中的细粒含量不变,即针对一种特定的土时孔隙比对冻胀的影响,因此得出的相关结论依然是合理的。

4 试验验证

王天亮等[5]对取自哈齐客专土料堆填场的粗粒土进行了干密度冻胀试验。该土细粒含量为11%,根据叶阳升等[3]的冻胀敏感性分类标准,属于弱冻胀敏感性土,本文采用文献[5]中的试验结果进行修正PCHeave模型验证,试验设置见图7。

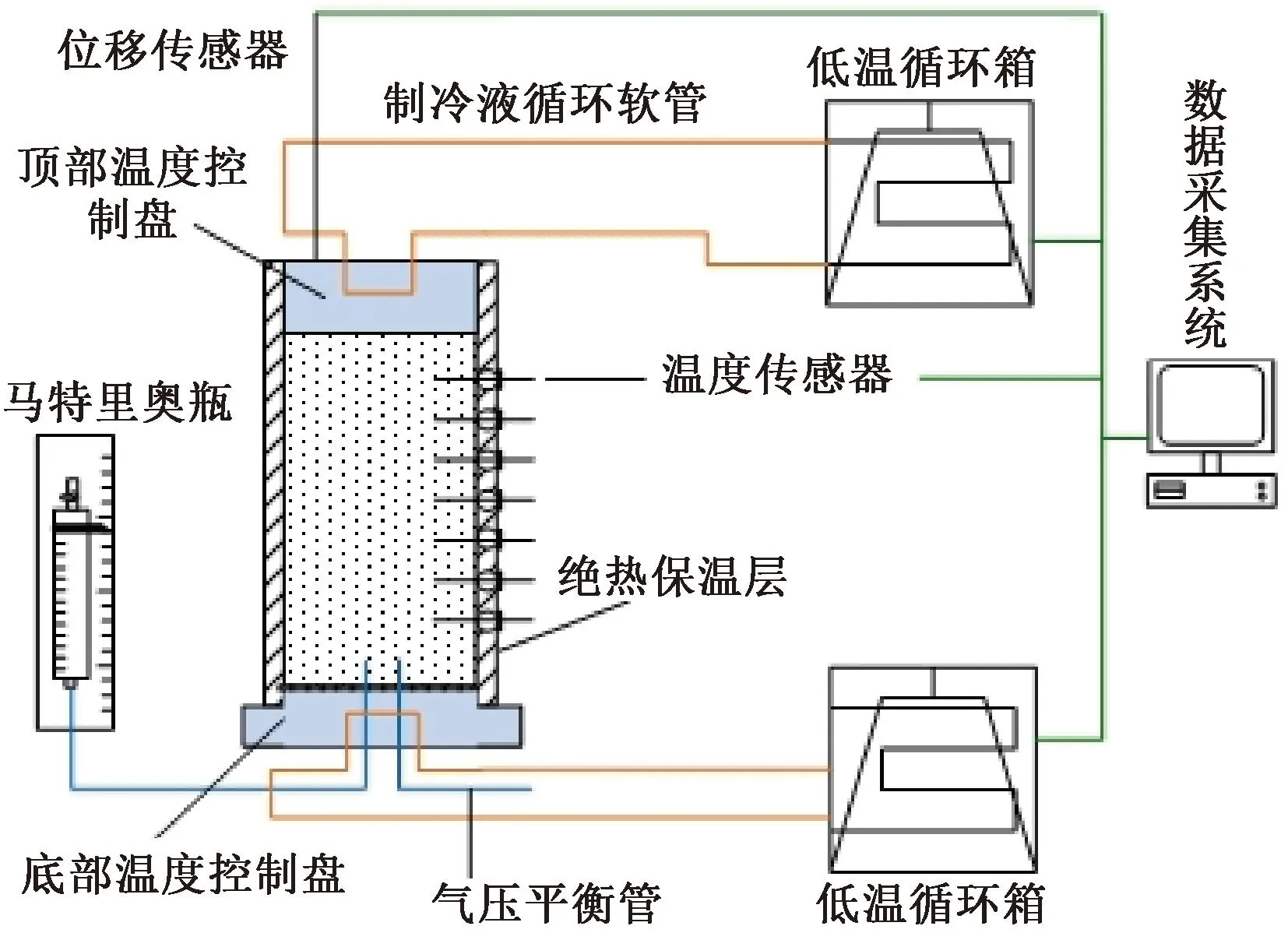
图7 试验设置示意

试样高16 cm,土粒比重为2.7,试样初始含水率为5.28%,土料饱和渗透系数为0.622×10-3cm/s。需要注意,饱和渗透系数是由原始土料所测得的,并没有考虑干密度变化对饱和渗透系数的影响,因此,本文采用式( 1 )来计算相应孔隙比的饱和渗透系数。对粗粒土及细粒掺量的颗粒级配曲线分析可计算得到有效粒径为0.1 mm。导热系数为3 W/(m·K),顶端温度为-5 ℃,底端温度为1 ℃,冻结时间为48 h。-1 ℃未冻水含量根据式( 2 )规律得到,即随孔隙比线性变化,a、b值与表1中-1 ℃相一致。修正PCHeave模型中粗粒土的计算物理参数见表2。试验验证结果见图8、图9。

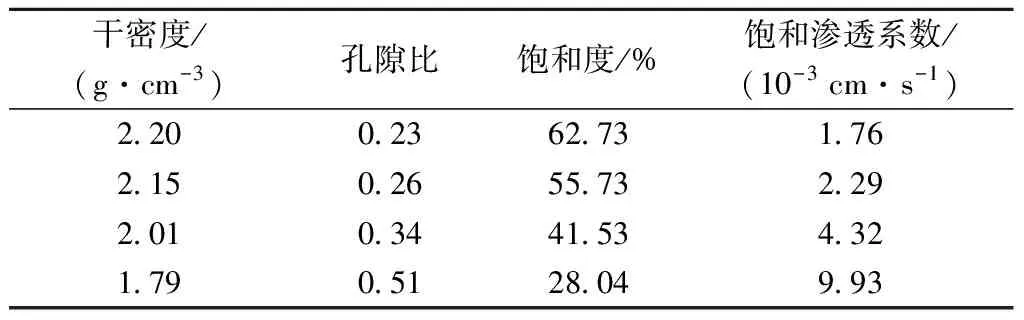
表2 修正PCHeave模型土体物理参数

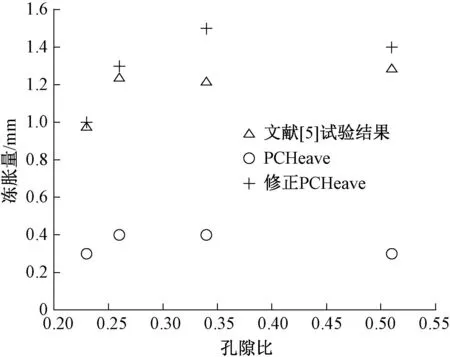
图8 孔隙比对粗粒土冻胀量的影响(试验验证)

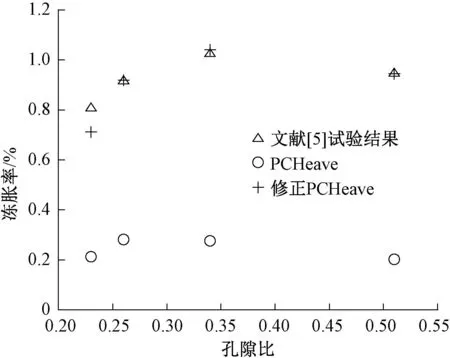
图9 孔隙比对粗粒土冻胀率的影响(试验验证)

由图8可以看出,粗粒土实测冻胀量随孔隙比增大,先增大再减小,这与第3节分析中同时考虑孔隙比对饱和渗透系数和未冻水含量时是一致的;尽管在孔隙比较大时冻胀量有一定的增大,但总体上新模型计算值与试验值吻合较好,且存在明显峰值。由图9可以看出,文献[5]的试验值与修正PCHeave模型计算值吻合非常好,且存在明显的峰值,与第3节分析一致。

若不考虑孔隙比对饱和渗透系数和未冻水含量的影响,仅把土料原始饱和渗透系数导入到原始PCHeave模型中,计算得到的冻胀量和冻胀率均远小于试验值。修正PCHeave模型考虑了未冻水含量随孔隙比的影响,未冻水含量减小抑制了冻胀产生,但同时孔隙比增大导致饱和渗透系数的增大,并促进了冻胀产生,且远大于不考虑这种变化时所计算的冻胀量,表明应当同时考虑孔隙比对饱和渗透系数及未冻水含量的影响,且孔隙比对冻胀弱敏感性土的冻胀影响不可忽视。

5 结论

我国严寒地区高铁路基填料和机场填方等工程具有严格的压实度要求,而考虑孔隙比的冻胀弱敏感性土冻胀影响研究尚未有系统性的理论分析。针对该问题,采用理论与经验分析相结合的方法,基于冻胀弱敏感性土孔隙比与渗透系数和未冻水含量之间的关系,建立了考虑孔隙比的修正PCHeave模型。基于该模型分析孔隙比与冻胀量、冻结深度和冻胀率之间的关系,并进行试验对比验证,主要得到以下结论。

1)同时考虑孔隙比对饱和渗透系数和未冻水含量的影响时,冻胀弱敏感性土的冻胀量和冻胀率均随孔隙比的增大而先增大再减小,存在一个最不利孔隙比,使冻胀量和冻胀率均可达到最大值;而冻结深度随孔隙比的增大而逐渐增大。

2)若仅考虑孔隙比对饱和渗透系数的影响,冻胀量和冻胀率均随孔隙比显著增加;若仅考虑孔隙比对未冻水含量的影响,冻胀量和冻胀率均随孔隙比减小,但减小幅度很小。

3)与粗粒土冻结试验的对比表明,修正PCHeave模型能够较好地描述孔隙比对冻胀弱敏感性土的冻胀影响。应同时考虑孔隙比对饱和渗透系数及未冻水含量的影响,且孔隙比对冻胀弱敏感性土的冻胀影响不可忽视。