高速铁路线路轨面坡度及竖曲线半径动态测量方法及应用研究

王 琰，陈仕明，魏世斌，余 宁，杨 飞，费继友

(1.大连交通大学 机车车辆工程学院，辽宁 大连 116028；2.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081)

我国高速铁路运营里程不断增加,列车运行速度不断提高,机车车辆在运行过程中的安全性和舒适性备受关注。作为轮轨系统的主要激扰源,轨道不平顺是引起机车车辆振动的主要原因,车辆振动不仅对旅客乘车舒适性有影响,严重时还会危及行车安全[1-7]。轨道不平顺定义为轨道几何形位相较于其设计参数的偏差。在线路开通运营前,轨道初始的不平顺往往与材料的缺陷、生产加工过程中的误差,以及施工过程有关;线路开通运营后,在轮轨相互耦合、车辆荷载、地基沉降以及其它外部因素的共同作用下,轨道的几何形位与设计参数的偏差越来越大,轨道不平顺进一步发展,直接影响列车安全。线路纵断面坡度及竖曲线半径是影响轨道线路平顺性[8-15]、弓网受流性能[16]以及机车动力性能[17]的重要参数,特别是在千米级大跨度铁路桥梁[18]。

快速、准确检测出轨道线路轨面坡度及竖曲线半径参数可为全面研究线路纵断面参数变化,以及和轨道长波不平顺、路基及大桥沉降关联提供线路实际数据基础,然而,当前国内尚无轨道线路轨面坡度及竖曲线半径动态检测装备。高速综合检测列车、轨道检查车等车载轨道检测系统[19-22],是动态检测线路不平顺的自动化装备,现有检测项目仅包括轨距、轨向、高低、水平(超高)、三角坑等轨道平面几何参数,也无轨道线路轨面坡度及竖曲线半径纵断面参数检测功能。

本文提出基于惯组的高速铁路线路轨面坡度及竖曲线半径动态测量方法,并以高速综合检测列车轨道检测系统为平台,在国内某新建高速铁路实车试验,相关技术成果已授权国家发明专利[23-24],为国内高速铁路轨道线路坡度及竖曲线半径动态检测技术提供了参考。

1 线路轨面坡度及竖曲线半径测量原理

线路的纵断面由坡度保持不变的平坡段和连接相邻两个坡度不同的平坡段的竖曲线组成,见图1。

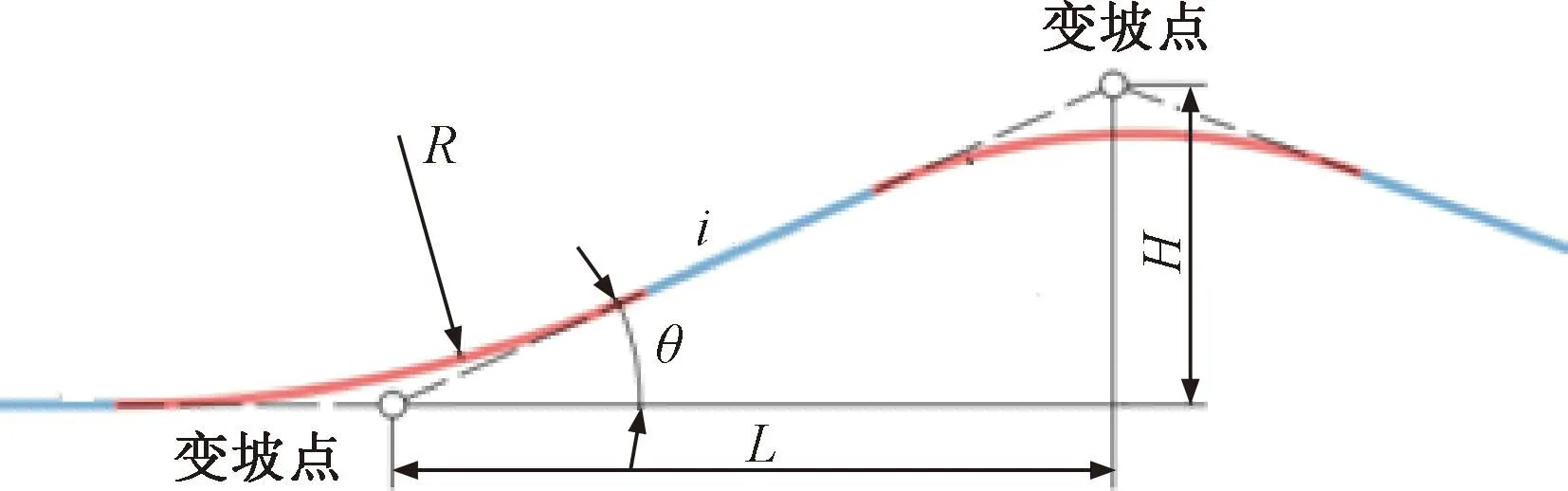
图1 铁路线路纵断面结构

图1中,变坡点为平道与坡道、坡道与坡道的交点;坡段长度L为相邻两变坡点间的水平距离,m;高度差H为相邻2变坡点的垂向距离,m;坡度大小i定义为相邻两变坡点高度差H与坡段长度L的比值,在我国通常以千分率表示,即

( 1 )

式中:i为坡度大小,取正值为上坡,取负值为下坡;θ为坡道段线路中心线与水平的夹角,定义为轨道纵向倾角。

按照TB 10621—2014《高速铁路设计规范》[25]规定,困难条件下线路最大坡度不应大于35‰,轨道纵向倾角最大值θ为

θ=2.004 53°=0.034 98 rad

( 2 )

由三角函数关系并结合工程应用,坡度大小计算式为

i=tanθ≈θ

( 3 )

基于高速综合检测列车轨道检测系统的惯组,解算其转向架构架位姿变化即可获得轨道纵向倾角,进而测量出线路轨面坡度大小。

变坡点处的坡度变化剧烈,为了避免列车经过变坡点时,出现脱轨、脱钩等危及行车安全以及附加加速度超过允许值等影响乘客乘车舒适度的现象,按照TB 10621—2014《高速铁路设计规范》[25]规定,正线相邻坡段的坡度代数差大于或等于1‰时,应采用圆曲线型竖曲线连接,如图1中红色线型,基于高速综合检测列车轨道检测系统空间等距采样距离、相邻采样时间轨道纵向倾角变化测量值的几何关系可计算出竖曲线曲率值,进而取倒数得到竖曲线半径R为

( 4 )

式中:ρ为曲率;Δx空间等距采样距离,通常情况取0.25 m;Δθ为相邻采样时间轨道纵向倾角变化测量值。

2 坡度及竖曲线半径动态测量方法

2.1 转向架构架及惯性坐标系建立及修正

高速综合检测列车轨道检测系统的检测梁与转向架构架刚性连接,惯组固定连接于检测梁,且无相对位移,惯组内部包含三轴高精度石英挠性加速度计和三轴高精度陀螺仪。转向架位姿变化可由惯组反映,轨道几何参数变化可由转向架位姿反映,建立测量基准坐标系,包括转向架构架坐标系和惯性坐标系,见图2。

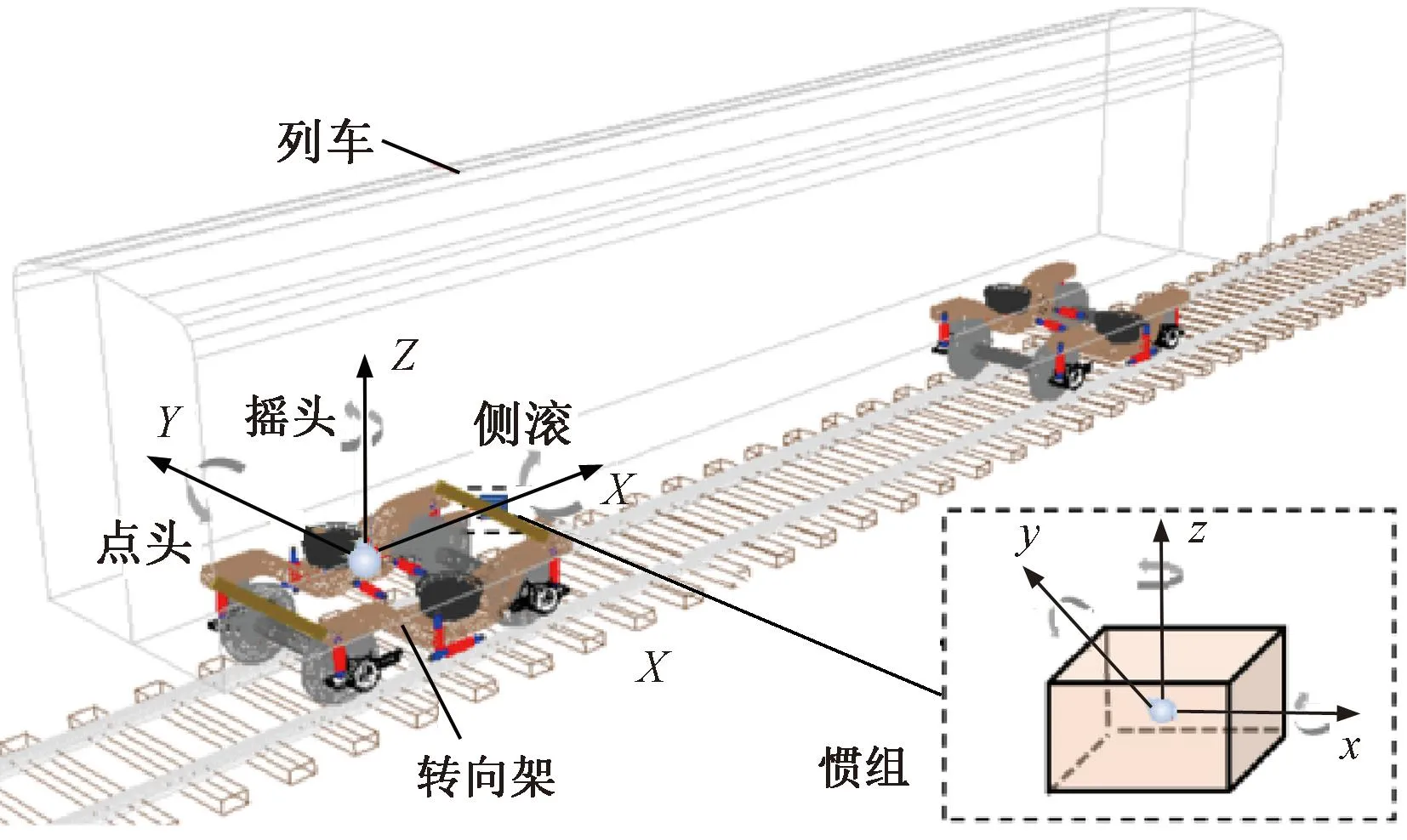
图2 转向架构架坐标系和惯性坐标系

图2中,定义列车前进方向为转向架构架坐标系X轴正方向,按照右手坐标系规则,Y轴正方向向左,Z轴正方向向上。同理,定义惯性坐标系x轴正方向为列车前进方向,按照右手坐标系规则,y轴正方向向左,z轴正方向向上。

由于惯组安装结构等偏差因素影响,惯性坐标系和转向架构架坐标系对应坐标轴很难严格保持平行一致,本文以重力加速度为参照、水平加速度极小相关性为基准修正对齐惯性坐标系和转向架构架坐标系,即测量过程中两坐标系对应坐标轴最大限度保持平行。

惯性坐标系和转向架构架坐标系修正对齐分为垂向修正对齐和水平修正对齐两个环节。转向架构架坐标系和惯性坐标系垂向修正对齐见图3。图3中,惯性坐标系xy平面为Q平面,转向架构架坐标系XY平面为P平面,假设两平面夹角为φ,转向架构架坐标系垂向单位向量Z=(0,0,1),惯组三向加速度位姿向量n=(xg,yg,zg)T,其中,xg,yg,zg分别为重力加速度g在对应三个坐标轴下的分量。

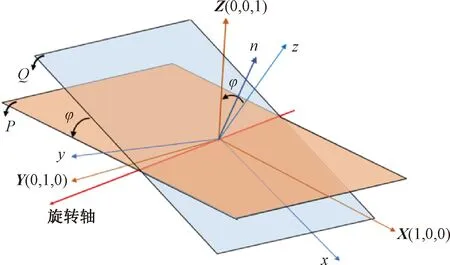
图3 转向架构架坐标系和惯性坐标系垂向修正对齐

列车静止时,以重力加速度为修正基准,重力加速度g为惯性坐标系三方向加速度向量合成值,即

( 5 )

将惯组三向加速度位姿向量n旋转至垂向单位向量Z,其与旋转矩阵M的关系式为

ZT=Mn

( 6 )

由Rodrigues旋转公式建立的关系式为

M(K,φ)=Icosφ+Ksinφ+(1-cosφ)uuT

( 7 )

s.t.

( 8 )

( 9 )

式中:I为3×3的单位矩阵。

由向量数学关系,即可得到惯性坐标系和转向架构架坐标系垂向修正夹角φ为

(10)

当列车静止时,惯组垂向加速度经过修正后,其值为重力加速度g,此时惯性坐标系xy平面与转向架构架坐标系XY平面平行。当列车运行时,惯组纵向加速度和横向加速度不包含垂向加速度分量,此时将3维坐标系修正对齐问题转化为二维问题。如图4所示,假设惯性坐标系xy平面和转向架构架坐标系XY平面对应坐标轴夹角为γ,惯组测量的横向加速度ax和纵向加速度ay实际是转向架构架横向加速度aX和纵向加速度aY的线性组合,即

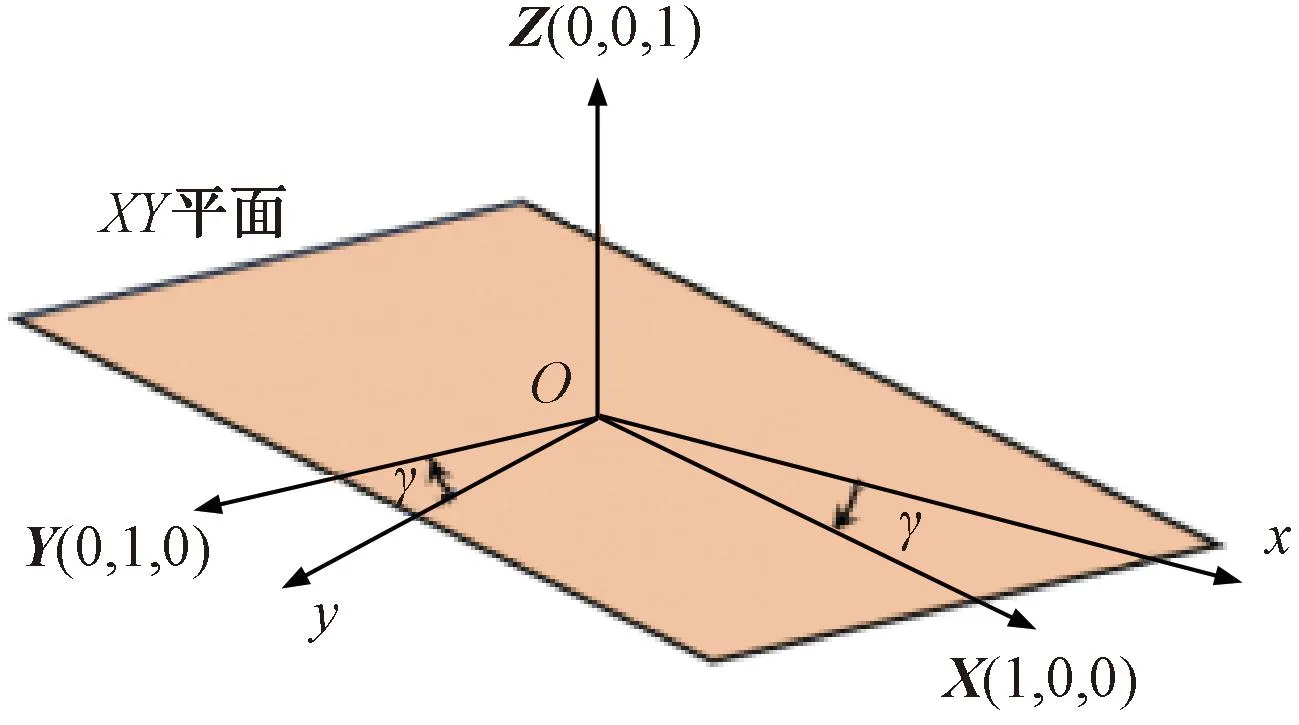
图4 转向架构架坐标系和惯性坐标系水平修正对齐

(11)

惯性坐标系和转向架构架坐标系水平修正对齐不同于垂向,垂向修正对齐以重力加速度为参照基准,水平修正对齐没有直观的参照基准。考虑到列车前进运动过程由于牵引或制动将产生纵向加速度,轨道结构等因素将产生横向加速度,理论上横向加速度与纵向加速度正交,故根据水平横向加速度与纵向加速度极小相关性,采用数学统计的方法获得水平修正夹角估计值,即求解水平加速度协方差最小时的夹角值γ为

E{[axγ-E(axγ)][ayγ-E(ayγ)]}=

(12)

式中:E(·)为数学期望;(axγ,ayγ)为(ax,ay)修正夹角γ后对应的加速度值。

由式(12)可以看出,水平加速度协方差最小时夹角γ为

(13)

综上,惯性坐标系和转向架构架坐标系修正对齐数学关系为

(14)

2.2 解算轨道线路轨面坡度及竖曲线半径

惯性坐标系和转向架构架坐标系修正对齐后,即所有测量对象均统一到同一个坐标系中。考虑列车与轨道纵向倾角和俯仰运动角偏差影响,建立线路轨面坡度测量模型,即线路轨面坡度θ为转向架构架对水平地面的绝对位姿角σ、列车与轨道平面纵向倾角α和俯仰运动角β的代数运算值,即

θ=σ-α-β

(15)

列车在坡道前进运动过程中,惯组测量的纵向加速度是车辆前进方向的真实加速度和重力加速度沿坡道分量的向量和,即

gsinσ=ax-atr

(16)

式中:atr为列车运行加速度,由列车轮轴端安装的光电脉冲编码器和采样时间计算得到,即

(17)

其中,x为列车前进位移;v为列车速度。

由三角函数关系并结合工程应用,由式(16)、式(17)计算转向架构架对水平面的绝对位姿角σ为

(18)

轨道纵向倾角α计算模型见图5。图5中,列车与轨道纵向倾角α可由转向架前端和后端垂向位移组件测量转向架和轨面垂向距离差Δh和两组件间距Δl计算得到,即

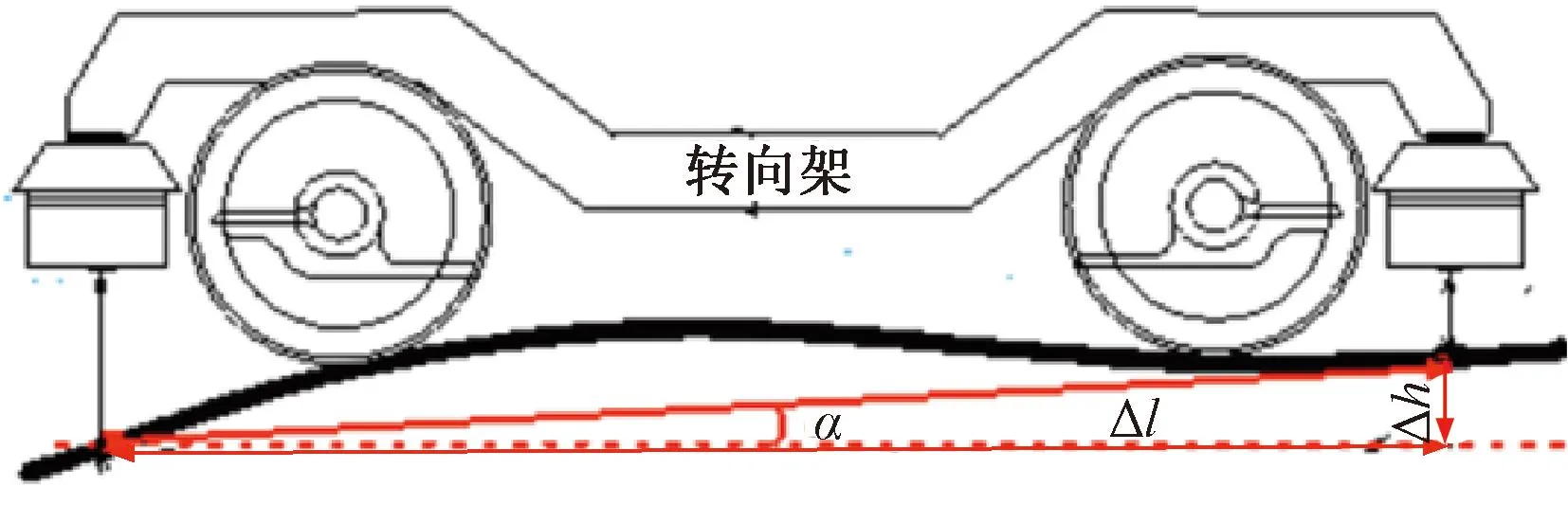
图5 轨道纵向倾角α计算模型

(19)

惯组点头陀螺敏感俯仰角β变化,考虑修正侧滚角误差,即

(20)

式中:ωy为点头陀螺角速度;ωz为摇头陀螺角速度;τ为侧滚角。

综上,基于转向架构架纵向加速度解算线路轨面坡度数学模型为

(21)

进而,结合式( 4 )可计算出竖曲线半径。

3 实车试验及分析

3.1 测量方法应用实现

高速综合检测列车轨道检测系统部分硬件安装位置及结构见图6。图6中,检测梁刚性连接转向架构架端部,惯性坐标系符合右手定则,安装时x轴方向指向列车前进方向,z轴方向垂直与检测梁上表面,检测梁两端分别安装垂向位移组件。基于高速综合检测列车轨道检测系统的惯组及垂向位移组件,解算其转向架构架位姿变化即可获得轨道纵向倾角,进而测量出线路轨面坡度大小,以坡度测量值为基础可解算竖曲线半径,测量算法实现逻辑见图7。

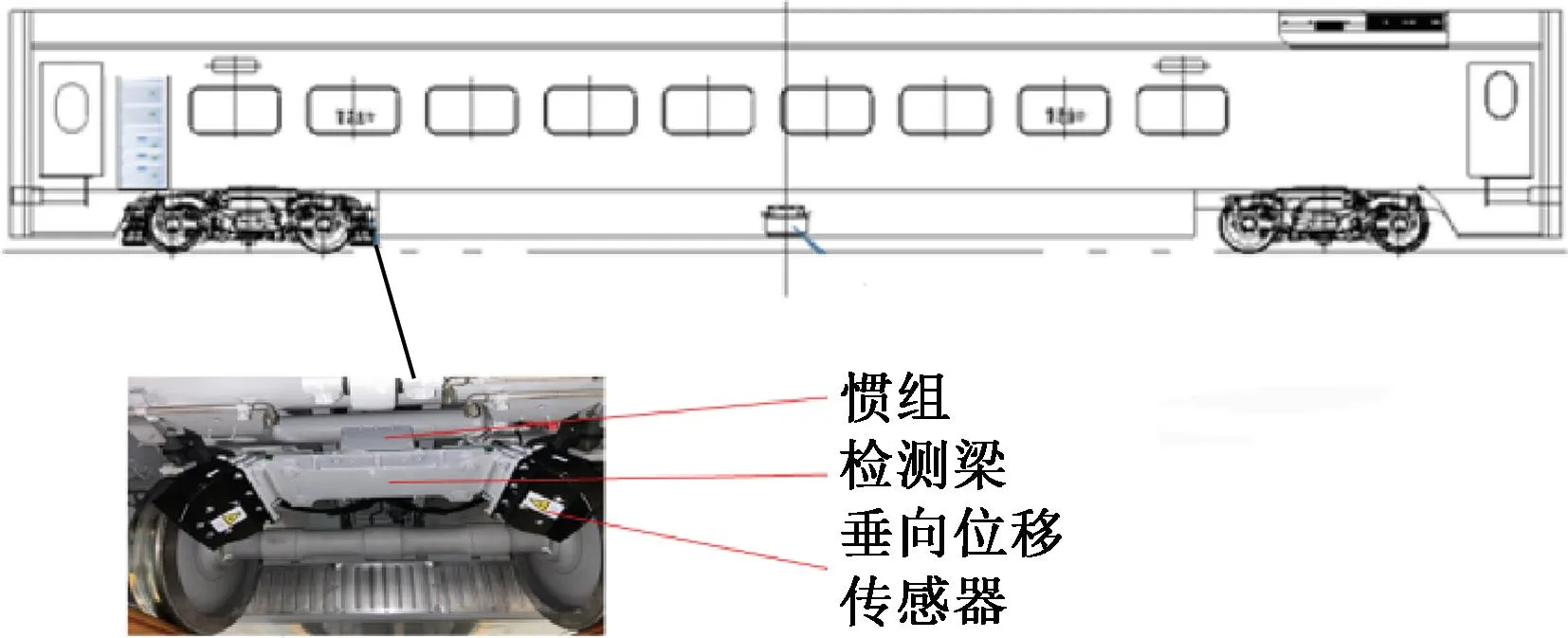
图6 高速综合检测列车轨道检测系统部分硬件安装位置及结构

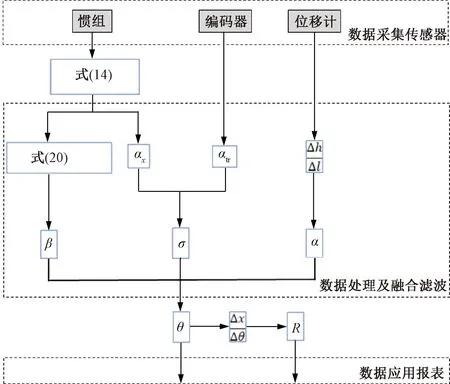
图7 线路轨面坡度及竖曲线半径动态测量算法实现逻辑

数据采集传感器包括六轴惯组、光电编码器和光学垂向位移组件,其中惯组内部包含三轴高精度石英挠性加速度计和三轴高精度陀螺仪。数据处理与融合滤波过程包括3条数据链和1个修正模块。3条数据链为:①惯组数据链,修正对齐惯性坐标系与转向架构架坐标系,惯组纵向加速计测量纵向加速度,点头陀螺测量俯仰角变化,摇头陀螺测量侧滚角误差,由俯仰角变化及侧滚角误差计算列车俯仰运动角β;②编码器数据链,由列车轮轴端安装的光电脉冲编码器和采样时间计算列车运行加速度atr,结合惯组纵向加速计测量纵向加速度及重力加速度分量计算转向架构架对水平地面的绝对位姿角σ;③垂向位移组件数据链,测量转向架和轨面垂向距离差Δh和两组件间距Δl计算列车与轨道平面纵向倾角α。修正模块用来补偿列车与轨道纵向倾角α和俯仰运动角β对解算轨道线路坡度带来的偏差。以坡度测量值为基础,基于空间等距采样距离、相邻采样时间轨道纵向倾角变化测量值的几何关系计算竖曲线曲率值,进而取倒数得到竖曲线半径。

3.2 实车测量数据分析

动态测量系统通常从重复性和准确性两方面进行评价。重复性评价试验分析高速综合检测列车在同一线路区间以不同速度或正向或反向运行多次测量结果之间的差异;准确性评价试验则采用外部测量手段或线路设计值对动态测量结果进行交叉验证,通常线路设计值为理论值,往往与实际值存在一定偏差。试验选择联调联试验收且尚未正式运营的国内某新建高速铁路作为试验线,以高速综合检测列车为载体,开展不同速度集下的动态“拉锯”试验,对本文提出的线路坡度及竖曲线半径动态测量方法进行评价分析。

试验线纵断面最大坡度代数差小于13‰,正线竖曲线半径为25 km,设计曲率为0.04 rad/km。选用的加速度计的零偏稳定性为200 μg,因此系统在静态情况下理论精度为0.2‰,坡度角测量值会存在0.2‰以内的固定偏差值,零偏值随时间而变化需定期标定补偿。加速度计每次上电时零偏值存在差异,是造成坡度角测量误差的主要原因。测量载体的俯仰角中包含了轨道高低不平顺,一个坡段的坡度角的极差约为1.2‰,导致所测量的坡度角分辨率不高。线路纵断面坡度角动态测量统计值见图8。由图8可知,一定截止频率的低通滤波器有助于提升坡度测量的信噪比,而对于线路实际坡度测量,区段范围内的拟合值更能直接反映真实坡度。

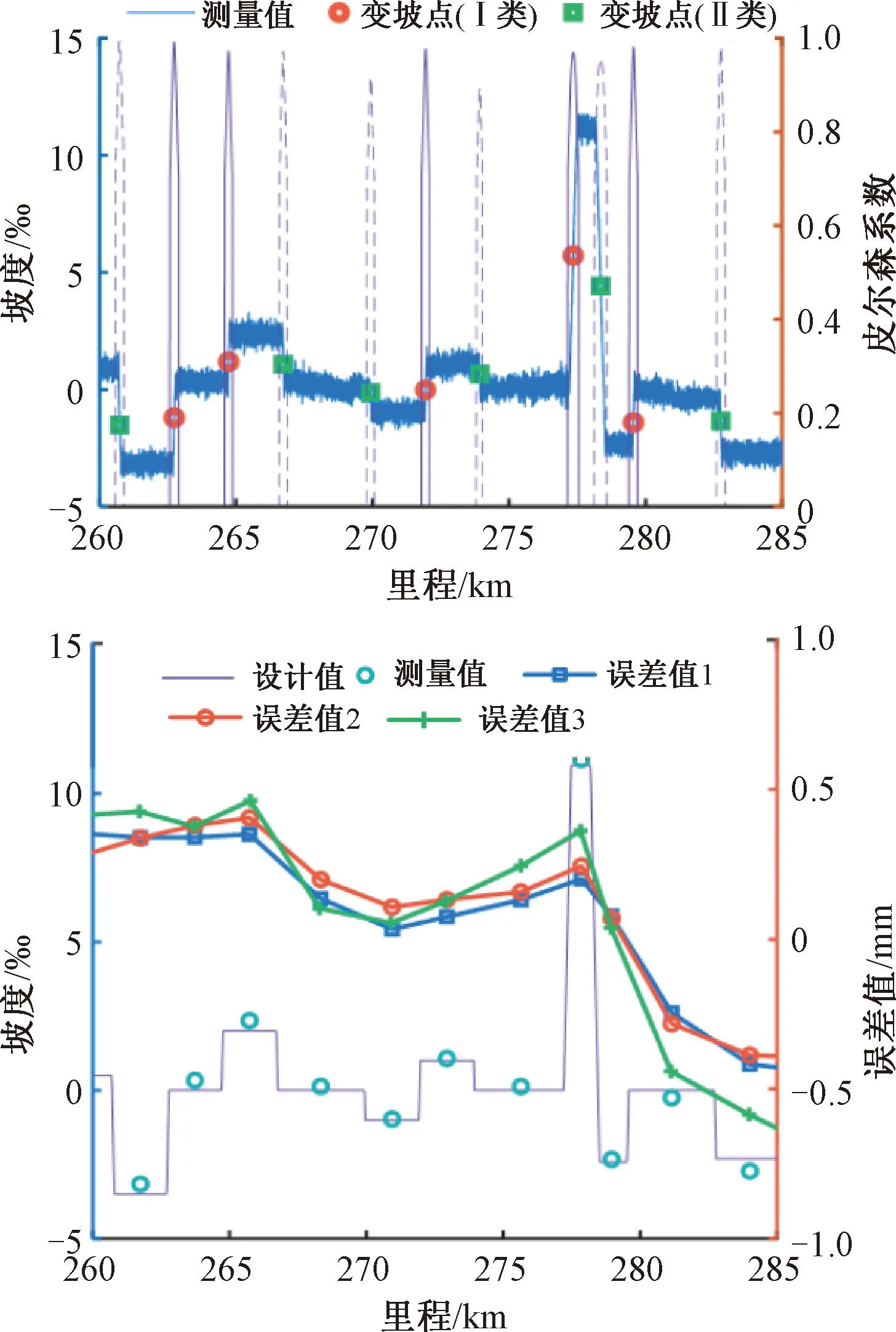
图8 线路纵断面坡度角动态测量统计值

坡度代数差Δθ、竖曲线长度l与曲率ρ,应满足Δθ=ρ×l。参考TB 10621—2014《高速铁路设计规范》[25],当高速线路相邻坡段坡度代数差大于或等于1‰时,应设置圆曲线型竖曲线相连接,正线坡度代数差应小于20‰。则最小竖曲线长度为25 m,最大竖曲线长度为500 m。由于列车行驶速度较快,检测数据对应里程受编码器累积偏差影响,与现场标记里程存在几米至几十米的偏差。计算坡度角实测值与坡度模板的Pearson系数并求得区段极大值,即为变坡点。速度为350 km/h线路的最小竖曲线半径为25 km,因此设置匹配模板的斜率一致,长度取线路竖曲线长度的中位数。以图8中里程K260—K285为例,该方法准确地识别了全线不同长度竖曲线对应的变坡点。Pearson相关性系数ρ(X,Y)是衡量向量X和Y相似度的一种方法,通常表示为

(22)

式中:μX、σX分别为序列X的均值、标准差。

图8中对比了3次典型实验(350 km/h同速度集下两次正向检测、一次反向检测)下的坡度角的重复性,统计重复性偏差的绝对均值为0.07‰,95%分位数为0.12‰。高速线路中坡段长度不应小于600 m,竖曲线长度小于500 m,因此分别变坡点向前、后推算300 m作为坡度测量的终止和起始点,作为坡度测量区段并统计拟合值,见图8。由图8可知,同向重复性偏差最大值为0.05‰,正反向重复性偏差最大值为0.1‰。对比了测量值与设计值间的偏差,发现坡度偏差的变化趋势较为一致,认为偏差主要是由建设过程中与台账设计值不吻合导致的。在运营维护期间,竖曲线坡度变化主要受线路整体沉降或线路捣固的影响,动态检测结果可监测该线路在全生命周期内的变化情况。

在行驶过程中,列车受轨道不平顺激扰或加减速惯性影响,检测梁与轨平面在俯仰方向的夹角不断变化。以里程K254为例,有无纵断面角度补偿条件下的测量值对比见图9。由图9可知,经过角度补偿后的坡度角处更为平滑,更加符合真实情况,说明检测方法的合理性。

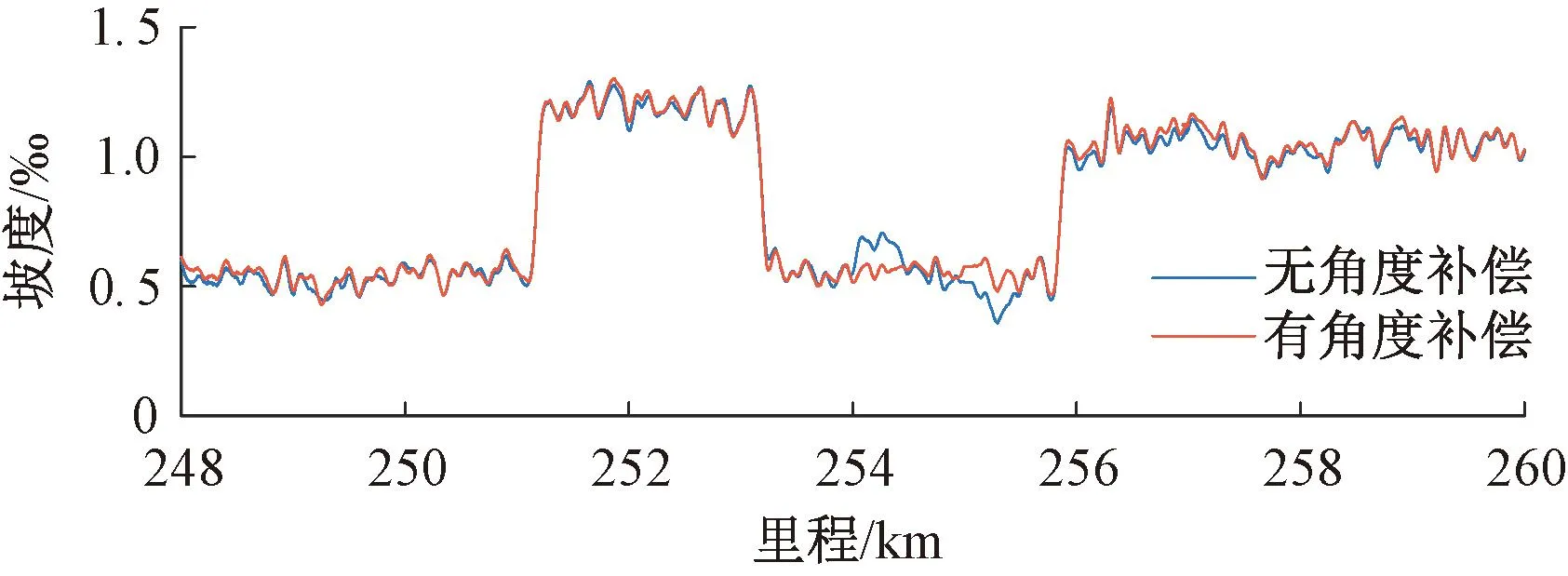
图9 有无纵断面角度补偿的坡度测量结果对比

3次典型实验重复性对比见图10。由图10可知,曲率在直线段中的高频成分主要由高低不平顺和测量噪声引起,重复性和再现性表现较为稳定。统计竖曲线曲率重复性偏差的绝对均值为0.71×10-3rad/km,95%分位数为1.76×10-3rad/km。

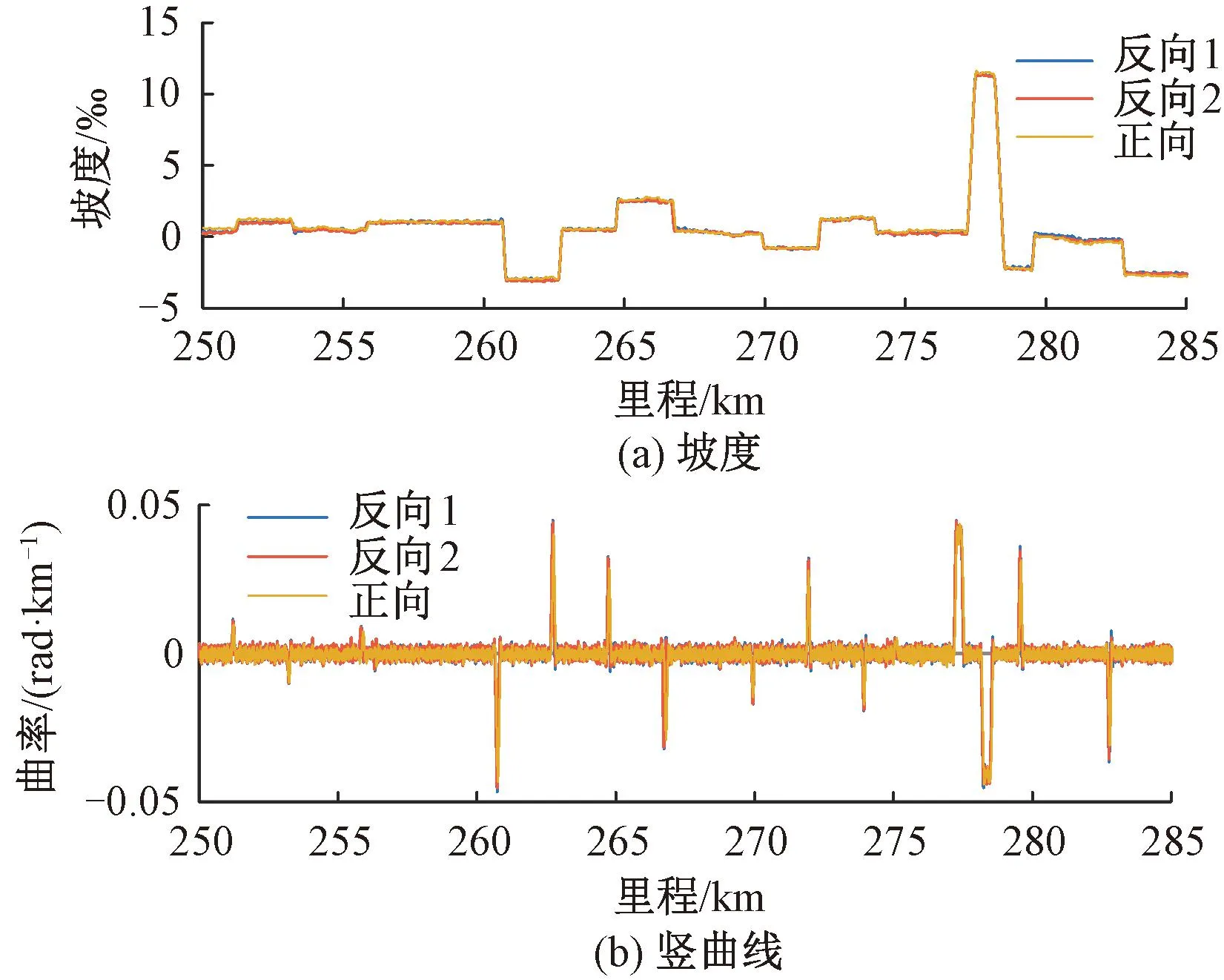
图10 不同方向下坡度和竖曲线曲率测量结果重复性

竖曲线曲率由陀螺仪测得,由于竖曲线半径较大,单位测量区间内陀螺仪的角增量接近传感器最小分辨率,测量信噪比较低。需采用低通滤波器对测量结果进行滤波,而低通滤波器阶数与滤波效果正相关,当坡度代数差较小、竖曲线长度较短时,滤波器会平滑衰减部分曲线段的曲率值,造成竖曲线曲率测量误差。选取两个典型竖向区段(区段1、2长度分别为333、50 m)分析最优滤波器截止波长,见图11。由图11可知,低通滤波器有效消除了高频噪声,由于区段1竖曲线长度较长,曲率最大值与设计值一致,当滤波器截止波长为100 m时,区段2的曲率值仅为0.025 rad/km。由此,对于高速铁路线路60 m是较为合理的滤波器截止波长,可取有效反应长度为50 m以上的竖曲线曲率。最后,在不同速度集(包含420 km/h高速)、方向下测得K278+500处的竖曲线曲率和该变坡点前一段坡度值,见表1。由表1可知,坡度角与竖曲线曲率的极差分别为0.22‰与0.005 rad/km。

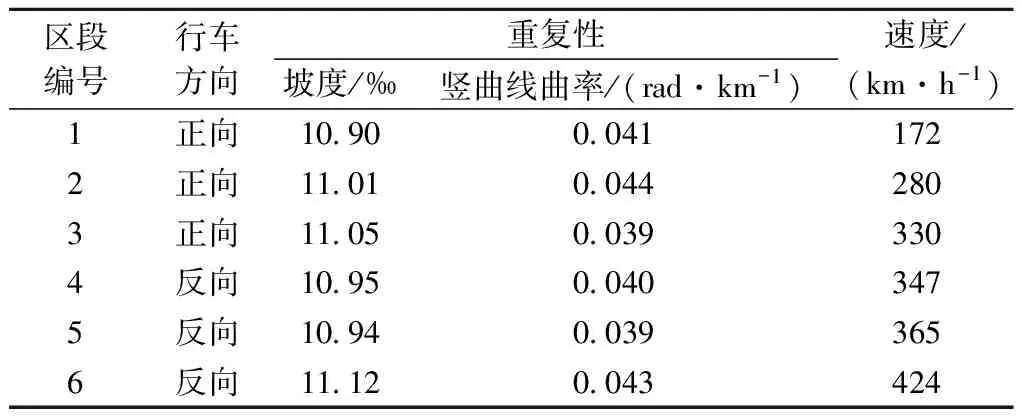
表1 不同速度集、方向下坡度和竖曲线曲率测量结果重复性

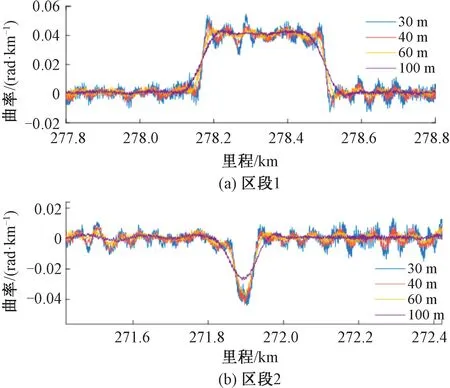
图11 不同滤波器下曲率值对比

与平面曲线相似,在高速行车条件下竖曲线会直接影响垂向加速度,进而影响行车舒适性。平面曲线通常采用正矢来评价圆顺度,而竖曲线曲线半径通常较大,对评价和管理提出更高的要求,未来可基于综合检测列车测量得到的高低20/40 m弦测值、坡度角和竖曲线曲率针对纵断面曲线研究出更科学的评价手段。

4 结论

1)采用转向架构架及惯性坐标系修正对齐,并补偿列车俯仰运动及与轨道平面纵向倾角误差,可以提高线路轨面坡度及竖曲线半径动态测量精度。

2)对速度为350 km/h高速线路,单位测量区间内角增量接近传感器最小分辨率,测量噪声较大,试验认为60 m是较为理想的滤波器截止频率,可有效反应长度为50 m以上的竖曲线曲率。

3)以国内主流高速综合检测列车轨道检测系统为平台,在国内某新建高速铁路线路进行实车试验,坡度重复性偏差的绝对均值为0.07‰,95%分位数为0.12‰,竖曲线曲率重复性偏差的绝对均值为0.71×10-3rad/km,95%分位数为1.76×10-3rad/km。开展多速度集下复现性能评估,坡度角与竖曲线曲率的极差分别为0.22‰与0.005 rad/km。

4)竖曲线半径通常较大,对评价和管理提出更高的要求,未来可基于综合检测列车测量得到的高低弦测值、坡度角和竖曲线曲率,针对纵断面曲线研究出更科学的评价手段。