振动轮两侧加速度差异及连续压实指标优化研究

2024-03-30刘泽潮冯怀平常建梅马德良

铁道学报 2024年3期

赵辉，刘泽潮，冯怀平，常建梅，马德良

(石家庄铁道大学省部共建交通工程结构力学行为与系统安全国家重点实验室，河北石家庄 050043)

连续压实控制技术通过实时分析振动轮响应,获得连续压实指标,以此对路基的压实质量进行实时检测。与传统压实质量控制方法相比,连续压实控制技术具有实时、全面、连续控制等优势[1-3],在铁路、公路、土石坝、机场等填筑体压实中得到了初步应用[4-7]。然而控制精度低限制了连续压实控制技术的进一步推广应用,这也是其无法取代传统压实质量控制手段的重要原因。Facas等[8]指出,由于土体横向刚度不均、振动轮结构偏心等原因,振动轮在压实过程中存在偏振及摆振的现象,而现阶段连续压实控制技术主要通过一侧的加速度响应反映土体的压实状态,这必将对压实质量感知精度产生一定的影响。因此,有必要研究压实过程中振动轮两侧振动响应特征及连续压实指标变化规律,为连续压实质量控制精度的提升提供理论与技术支撑。

振动轮偏振、摇摆的现象普遍存在,研究者从产生机理、幅值差异等多方面进行了研究。为分析摇摆及偏振产生的机理,侯劲汝等[9]结合偏振模型,认为振动轮的激振力作用中心面与振动轮质心的重合度是导致振动轮两侧振幅不均匀的关键因素。赵利军等[10]利用橡胶轮胎提供均质边界条件,测试了振动轮的空间振动情况,发现振动压路机存在振动轮横向振幅不一致现象。可以看出,振动轮结构不对称、两侧土体刚度不均会使振动轮两侧产生不同的响应特征。为分析两侧振动响应差异,Kenneally等[11]利用数值方法研究了压路机与路基相互作用关系,并通过振动轮左右安装加速度计的现场试验揭示了振动轮的摇摆特征。龚涛等[12]通过建立二维轮-路振动模型及数值仿真,发现填料横向刚度及阻尼的差异会导致振动轮两侧振动幅值显著不同。Facas等[8]建立了体现振动轮与机架摇摆状态的动力学模型,通过仿真的手段,获得了沿振动轮横向刚度分布不均情况下的振动轮两侧加速度差异。上述研究对振动响应中的偏振与摇摆产生的机理进行了深入分析,但偏振与摇摆对连续压实指标的影响研究尚不充分。

本文结合振动压实现场试验,通过采集压路机振动轮两侧的加速度信号,研究不同压实遍数、振动频率下,振动轮两侧加速度峰值、连续压实指标、倍频幅值的变化与分布规律。提出考虑双侧响应的连续压实指标,通过相关性分析,验证指标的准确性,为提升压实控制精度提供参考。

1 现场试验

1.1 场地及设备

本试验在某国家重点试验室进行,场地大小为100 m×76 m(长×宽)。按照JTG E40—2007《公路土工试验规程》[13],对现场土体进行基本物性试验,取土深度约为30 cm。填料为含粗粒的粉质土,物理特性参数见表1。

表1 土体物理特性参数

试验所用的振动设备为柳工CLG6118型压路机,工作重量为180 000 kN,振动频率为30/32 Hz,振幅为1.9/0.9 mm,振动轮宽度为2 100 mm。数据处理与采集采用动态数据采集仪和IEPE压电式加速度传感器,量程为100 m/s2,灵敏度为100 mV/(m/s2)。设置采样频率为1 024 Hz,试验实时数据在驾驶室内的计算机上显示并记录。为考虑压路机振动轮两侧的振动响应,在振动轮的两侧轴端安装加速度传感器。加速度传感器布设位置见图1。

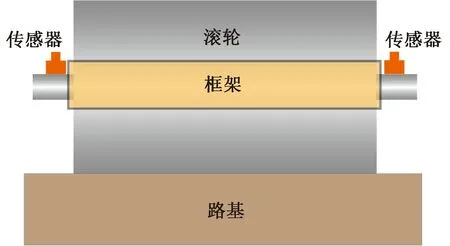
图1 传感器布设位置示意

1.2 试验方案

试验测点布置见图2。设置尺寸为20 m×2 m的碾压带,沿行进方向每隔2 m布置2个测点,共布设5组检测点,依次编号为1#、2#、3#、4#、5#,两测点位置间隔为1.6 m,距碾压带边缘25 cm。为避免启动与熄火时振动轮频率不稳定的情况,测点布置在碾压带的中间区域。

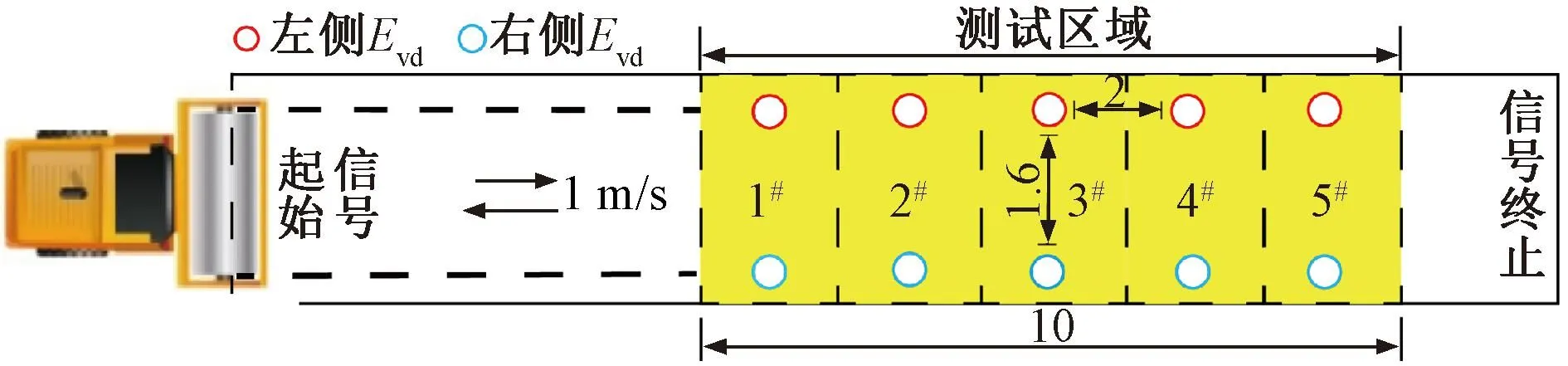
图2 测点布置(单位:m)

在振动压实前进行往复一周的静压,以达到预压及整平土基的目的,避免土基不平整带来的误差。含水率对土体的回弹模量存在着显著影响[14-15],通过洒水晾晒的方式将含水率控制在(14.2±1)%。在检测点位上测试土体静压后的动态变形模量Evd,然后对土基进行振动压实。研究表明,相较于振动频率,压路机行驶方向对压实计值CMV的影响很小[16]。为了缩短试验周期,行车方向分为正向与反向两种形式,反向压实时压路机不掉头,以倒车的形式压实。根据现场压实经验,振动压实4遍即可达到最大的压实程度,因此,在静压整平土体后振动压实了4遍。振动频率采用30/32 Hz,即进行2遍弱振,2遍强振,以研究不同激振力对测试的影响。4遍振动压实控制行车速度在1 m/s左右。每遍压实后在测点处检测Evd。试验方案见表2。

表2 试验方案

2 试验结果与分析

2.1 加速度峰值差异性

振动轮加速度是连续压实指标计算的重要依据,受路基刚度、激振力等多种因素影响。为研究振动轮空间响应特征,分析了不同压实遍数下振动轮两侧加速度峰值与Evd的变化规律。加速度峰值取加速度峰峰值的1/2,振动轮两侧加速度峰值差异ΔAi为

( 1 )

式中:AL,i、AR,i分别为第i遍压实左、右侧加速度峰值;i为压实遍数,i=1～4。

在5组检测点上提取振动轮两侧的加速度峰值,振动轮两侧加速度峰值对比见图3。图3中,当数据点落在45°线(直线x=y),表示两侧峰值相等,L1、L2均为数据点的包络线。由图3可见,数据点均匀分布于45°线的左上方,表明不同压实遍数下右侧加速度峰值始终大于左侧。这是由于振动轮结构偏心造成的右侧加速度峰值始终大于左侧。随着压实遍数增加,加速度峰值也随之增大,在第3遍压实后达到峰值,第4遍后峰值略有下降。这是由于土体刚度增加会导致土体共振频率变大,当共振频率高于振动频率时,加速度峰值会随着压实遍数的增加而降低。由图3还可见,随着压实的进行,L1逐渐向45°线靠近,表明左右峰值差异逐渐减小。但L2始终与45°线平行,说明左右峰值存在固定差异。由此可见,造成两侧峰值差异主要有两个原因:压路机系统自身的结构偏心,其对加速度峰值的影响不会随着压实的进行而减小;土体刚度横向不均,随着压实遍数的增加,土体均匀性提升,刚度不均的影响逐渐减小。

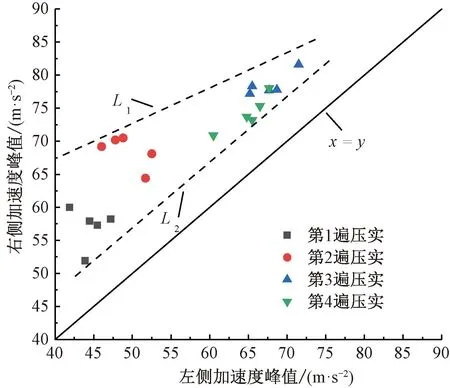
图3 振动轮两侧加速度峰值对比

不同压实遍数下5组测试点位上加速度峰值左右差异均值分别为24.4%、32.4%、14.8%、13.3%。可以看出,随着压实遍数的增加,两侧的峰值差异先增大后减小,在第2遍压实后差异均值最大。相关研究表明[17],随着Evd增加,加速度峰值呈现先增大后减小的趋势。两侧峰值增大程度的不同导致第2遍压实差异明显增大,随着压实的进行,土体均匀性进一步提升,两侧加速度差异逐渐减小。

5组检测点上振动轮两侧土体Evd对比见图4。由图4可见,第1、2遍数据点分布于45°线两侧,而第3、4遍的数据点分布于45°线的左上方,且数据点呈现出逐渐聚集的趋势。不同压实遍数下两侧Evd差异均值分别为24.4%、14.2%、11.4%、6.9%,这表明压实初期,土体两侧刚度差异明显,随着压实的进行,由于自身的结构偏心引起的持续偏振,使得右侧Evd逐渐大于左侧,且压实的均匀性有所提高。

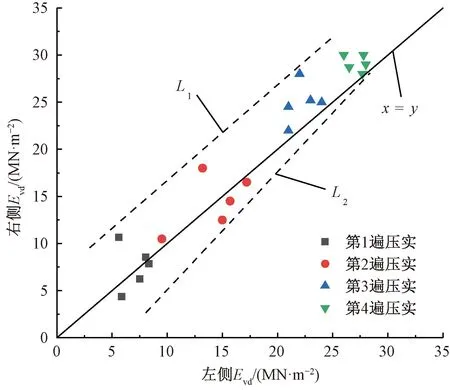
图4 振动轮两侧土体Evd对比

振动轮两侧加速度峰值与Evd的关系见图5。由图5可见,拟合线相距较远,这表明在相同Evd下,两侧加速度峰值差异明显。数据较为离散,但整体呈现增大趋势,表明随着Evd的增大,加速度峰值整体呈现增大趋势。连续压实指标与传统检验指标的相关性校验时,相关系数应大于0.7[18]。通过回归分析发现,两侧加速度峰值与Evd的相关系数分别为0.79、0.74,表明两侧加速度峰值与Evd相关性较好。因为加速度峰值在压实度到达一定程度时会出现下降的趋势(见图3),与图4中Evd的变化趋势相悖。因此不能将加速度峰值单独作为连续压实指标。

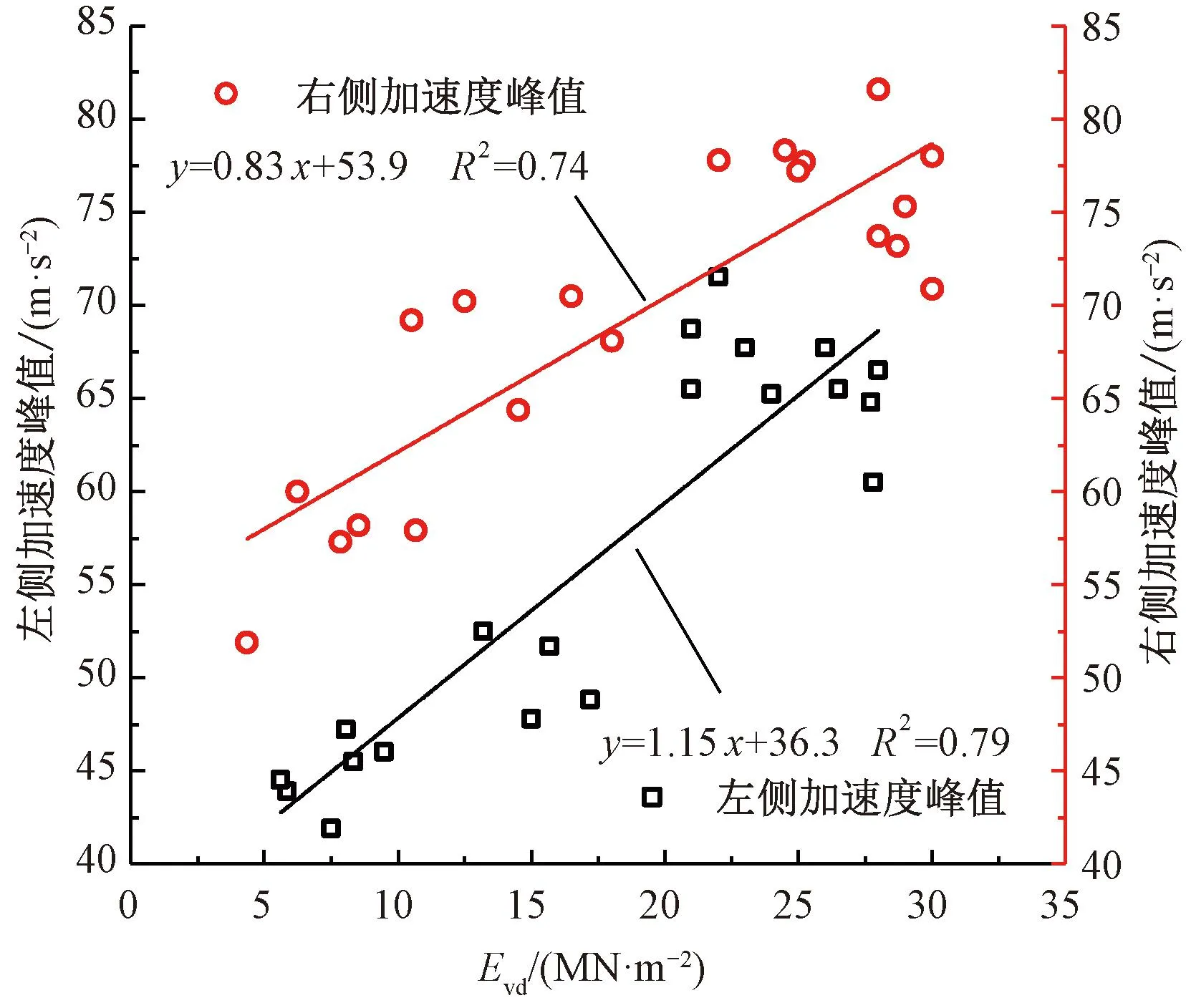
图5 加速度峰值与Evd关系

2.2 连续压实指标差异性

谐波类指标最早被用于评价土体的刚度,其通过不同谐波对应幅值组合计算得到。本文采用的谐波类指标为压实计值CMV,连续压实值CCV。为消除原始信号包含的高频信号,同时为了包含振动加速度三次谐波分量,采用低通截至频率为100 Hz。每隔0.5 s对滤波后加速度进行傅里叶变换。

CMV、CCV计算式分别为

( 2 )

( 3 )

式中:C为常数,C=100;a1.0f、a0.5f、a1.5f、a2.0f、a2.5f、a3.0f分别为基频1.0f、0.5f、1.5f、2.0f、2.5f、3.0f对应的加速度幅值。

为研究振动轮两侧响应差异对连续压实指标的影响,同时分析两侧连续压实指标的变化规律,采用箱线图描述同一遍压实下压实路径上所有的连续压实指标分布。不同压实遍数下两侧CMV、CCV的分布规律分别见图6、图7。

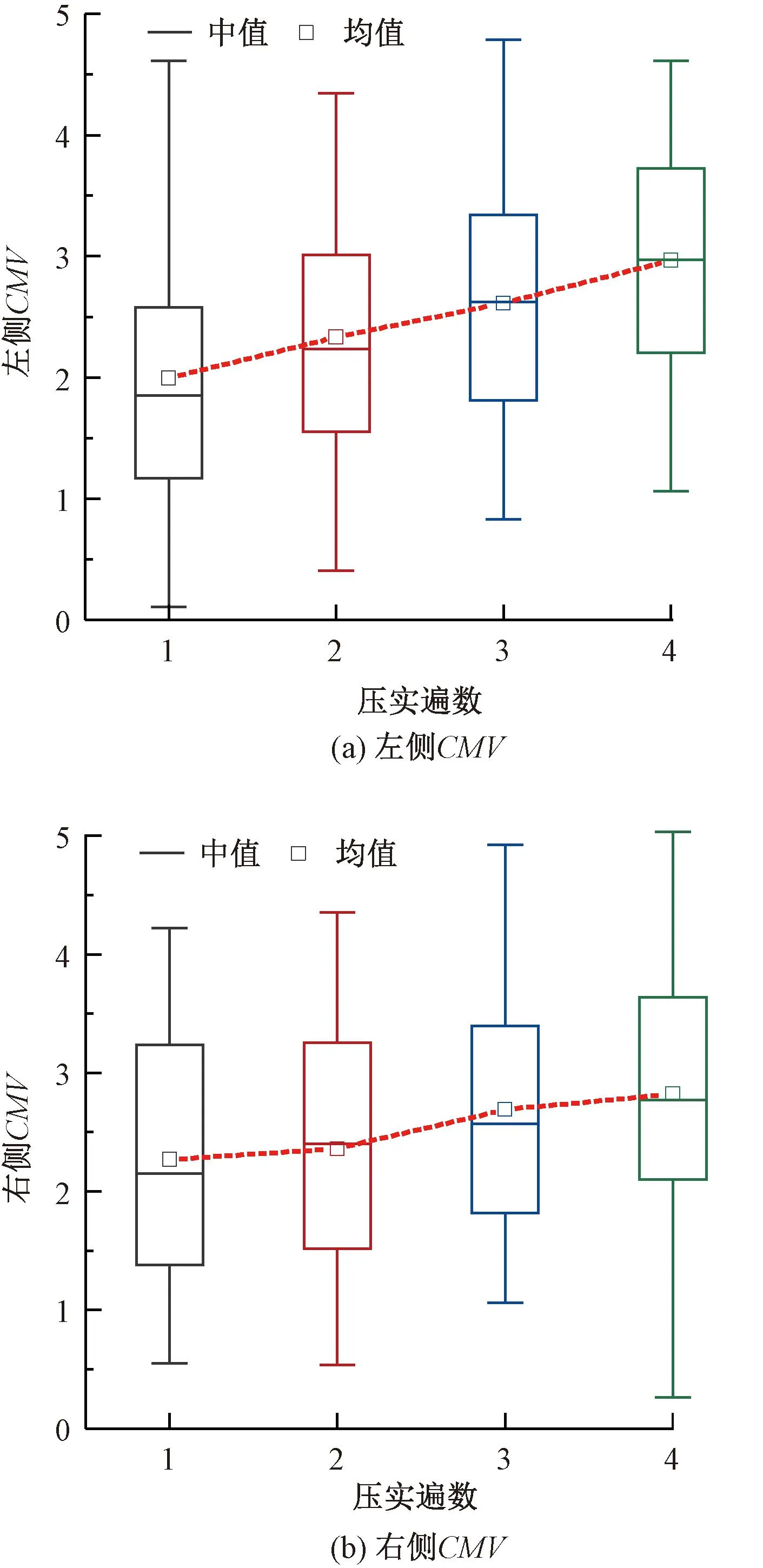
图6 振动轮两侧CMV分布

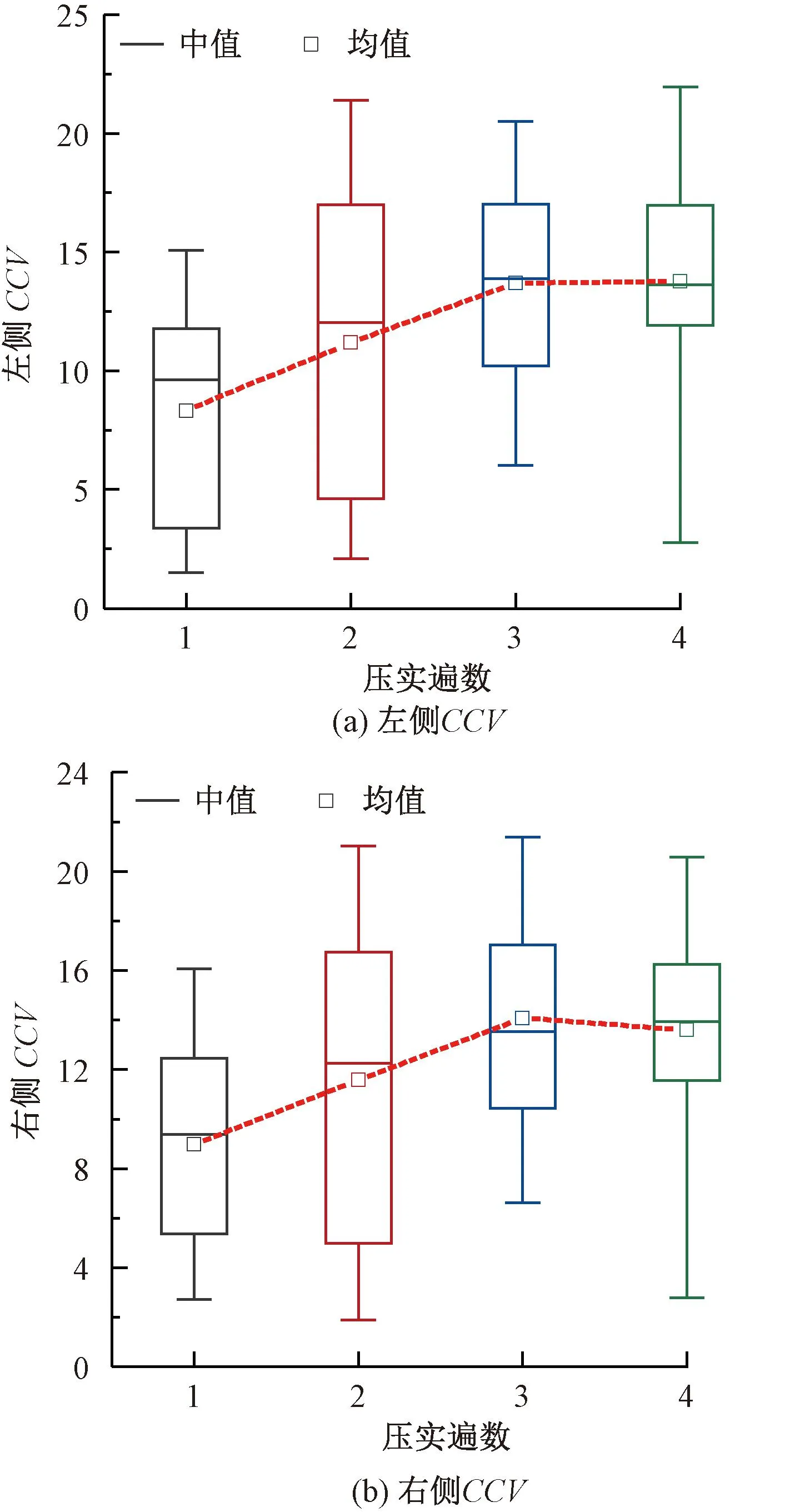
图7 振动轮两侧CCV分布

由图6可见,两侧CMV均值随着压实遍数的增加均显示出增大的趋势。单侧CMV在相同压实遍数下四分位差值大小几乎一致,表明每遍压实下CMV数据离散程度相同。在压实过程中,随着压实遍数的增加,路基压实度应趋于一致,其刚度的差异性也应逐步减小[19]。由此可以看出,CMV的数据分布并不能体现土体均匀性变化。

由图7可见,两侧CCV均值随着压实遍数的增加而增大。但在第4遍压实时,CCV并未有明显的增长,甚至右侧的CCV数值略有下降。而CCV在压实初期数值明显较为离散,随着压实遍数的增加,数据逐渐聚集,这与实际压实过程中土体均匀性的变化规律相吻合。在第4遍压实时出现异常点,异常点均分布在CCV较小的一侧,这可能是由于过压导致的。

两个测量值变化规律的差异与指标的定义有关,CCV不仅考虑了二次谐波,同时也包含了加速度频谱中的次谐波分量。有研究表明[20]基频与高次谐波主要反映了被压土体的不均匀性,次谐波反映了振动轮与土体的接触情况。因此,CCV反映了土体的非均匀性,也能体现出了土体过压时的变化。

由两侧CMV、CCV变化规律可以看出,两侧的CMV、CCV的上四分位数、下四分位数、均值均呈现出相同的变化趋势。且不同压实遍数下两侧指标离散程度几乎相同,只是在均值与中位数数值大小上存在差异。表明现场压实时,并不能通过简单的标定消除振动轮空间振动引起的测量值数值上的差异,在控制压实质量时需要同时考虑双侧的连续压实指标。

为研究两侧测量值差值大小及数值的变化规律,定义CMV、CCV的左右压实差值ΔCMV、ΔCCV分别为

ΔCMV=CMVR-CMVL

( 4 )

ΔCCV=CCVR-CCVL

( 5 )

式中:CMVR、CCVR分别为振动轮右侧加速度信号计算CMV、CCV;CMVL、CCVL分别为振动轮左侧加速度信号计算CMV、CCV。

同一遍压实下沿压实路径上所有的ΔCMV、ΔCCV分布情况见图8。由图8可见,不同压实遍数下ΔCMV、ΔCCV的中位数与均值均大于0,表明在振动轮右侧测量值普遍大于左侧,且两侧差值的大小与压实遍数无关。说明这是由于振动轮偏振造成的,与土体横向刚度不均无关。ΔCMV最大值为1.67,两侧变化幅值达69%,ΔCCV最大值为3.79,两侧变化幅值达55.2%。由此可见,不同侧的加速度计测试土体刚度时存在显著差异。

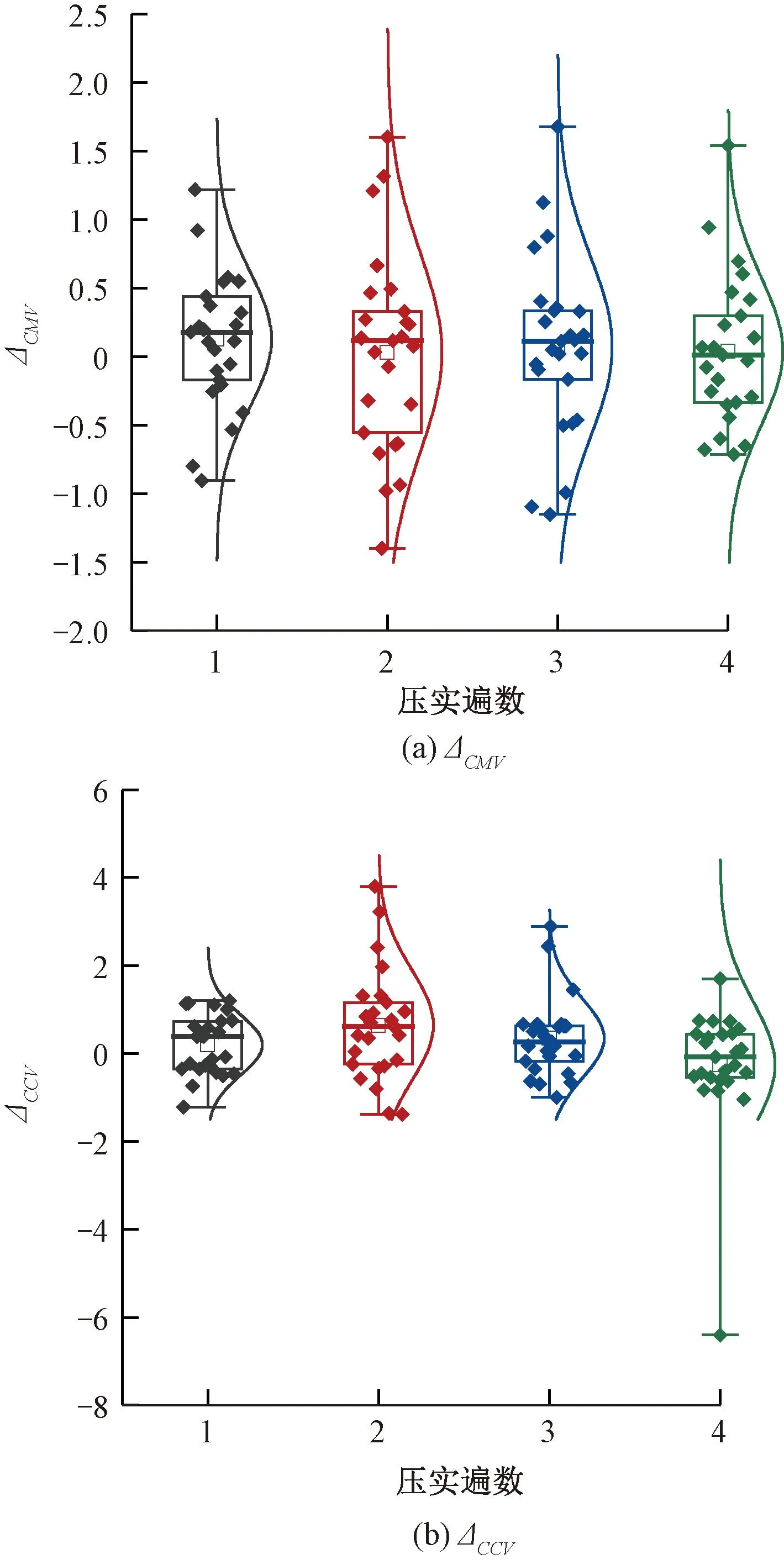
图8 连续压实指标差异值分布

弱振时,ΔCMV、ΔCCV分布较强振时更为离散,说明在压实初期,土体均匀性差,两侧测量值差异大。随着压实遍数的增加,数据逐渐集中,土体均匀性逐渐提高。

2.3 谐波类指标差异产生机理分析

计算左、右两侧响应的各个倍频所对应的幅值差异diffR-L,计算式为

( 6 )

式中:aif-L、aif-R分别为左、右侧各倍频对应的幅值,i=0.5、1.0、1.5、2.0、2.5、3.0。

两侧各频率分量下的加速度幅值差异见图9。由图9可见,两侧1.0f对应加速度幅值差异分布十分集中,中值均大于0,并未出现异常点。两侧2.0f、3.0f的加速度幅值差异分布相较于其他倍频较为分散。出现明显的异常点且均位于中位数下,3.0f呈现偏态分布,表明左侧的幅值大于右侧幅值情况居多,造成负值偏多。0.5f、1.5f、2.5f的加速度幅值差异分布较为集中,均值均位于0附近。

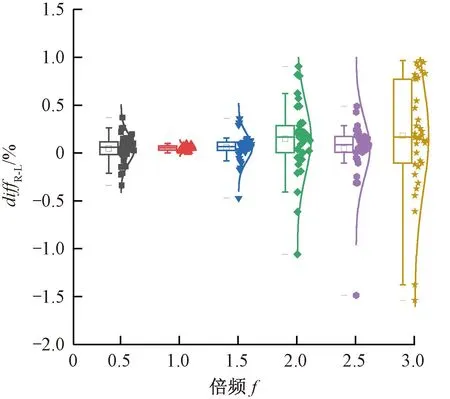
图9 振动轮两侧各倍频对应的加速度幅值差异

为探究连续压实指标差异产生的原因,首先对轮下土体的均匀性进行分析。将同一压实遍数下,振动轮两侧的土体动态变形模量Evd见图10。

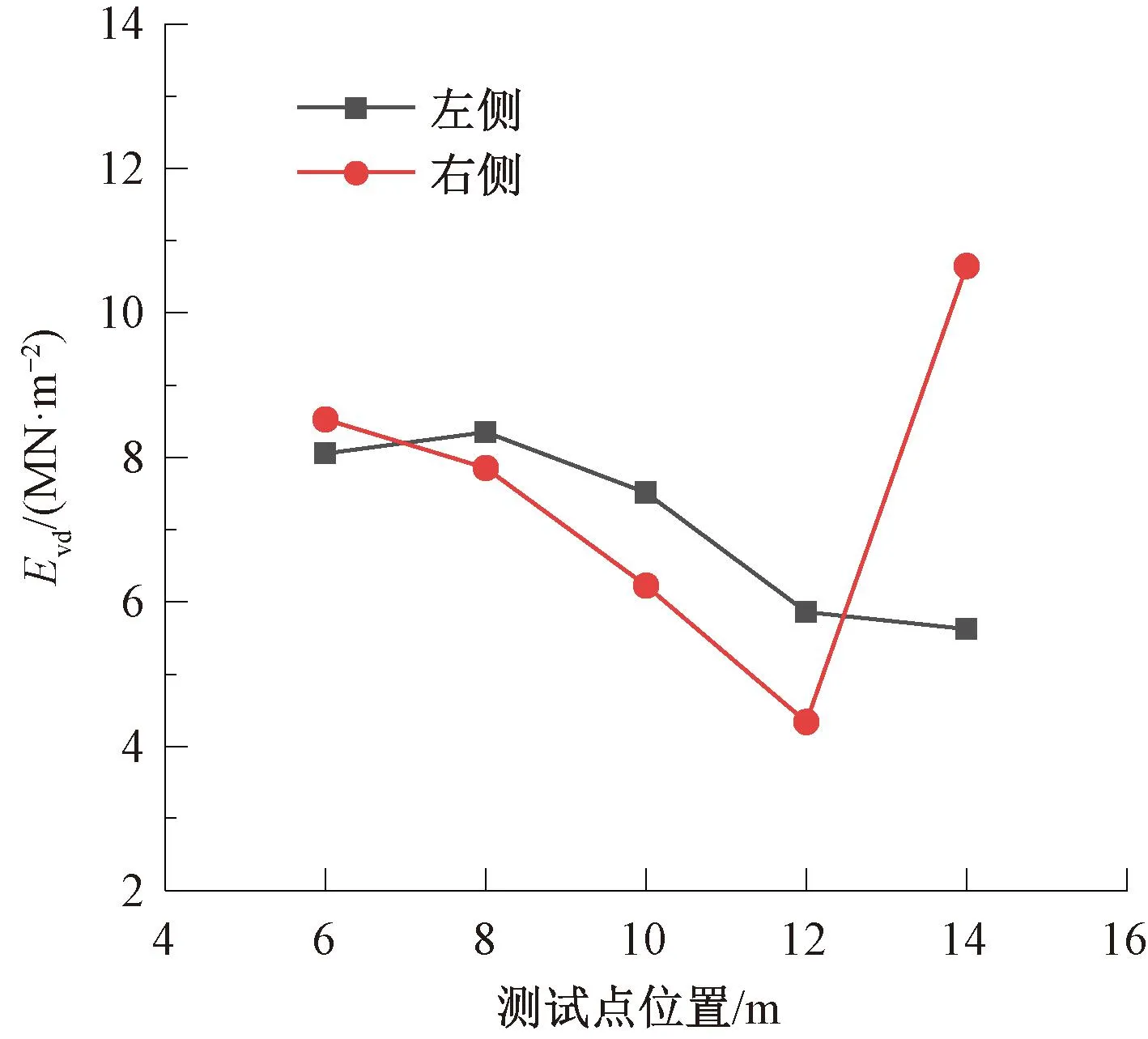
图10 振动轮两侧土体Evd

由图10可见,振动轮两侧土体压实程度并不一致。在6、14 m位置处,右侧Evd要大于左侧,尤其14 m处,两侧差距明显。

振动轮两侧响应的整数倍频(1.0f、2.0f、3.0f)幅值见图11。由图11(a)可见,振动轮右侧加速度响应基频幅值始终大于左侧,并未受到被压土体刚度分布不均的影响。这与基频的定义有关,基频代表了压路机激振力的频率,基频幅值是频谱图中最大的加速度幅值,其右侧大于左侧说明是由振动轮自身结构造成的。图9中1.0f加速度幅值差异分布集中,只是均值略大于0。进一步证明了这是由于振动轮结构偏心带来的固有差异。

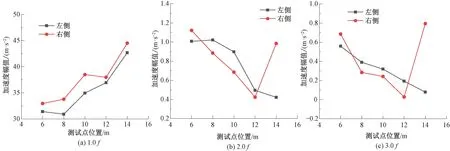
图11 振动轮两侧响应的整数倍频幅值

由图11(b)、图11(c)可见,对于基频的整数倍频幅值,即2.0f、3.0f的加速度幅值,与图10中两侧Evd的变化趋势一致,在14 m位置处右侧显著大于左侧。表明整数倍频的加速度幅值与两侧Evd有着显著的相关性。这说明整数倍频能反映出土体的压实特性。两侧压实状态不均会引起振动轮整数倍频幅值的变化。

振动轮两侧响应的非整数倍频幅值见图12。由图12可见,对于基频的非整数倍频幅值,即0.5f、1.5f、2.5f,与两侧Evd未展示出显著的相关性,这表明非整数倍频幅值受到两侧压实状的影响较小。0.5f右侧始终大于左侧的加速度幅值,与1.0f的加速度幅值类似,说明此频率受到振动轮机械结构的影响较大。1.5f、2.5f受到机械结构偏心与土体不均耦合影响,并未表现明显的规律性。

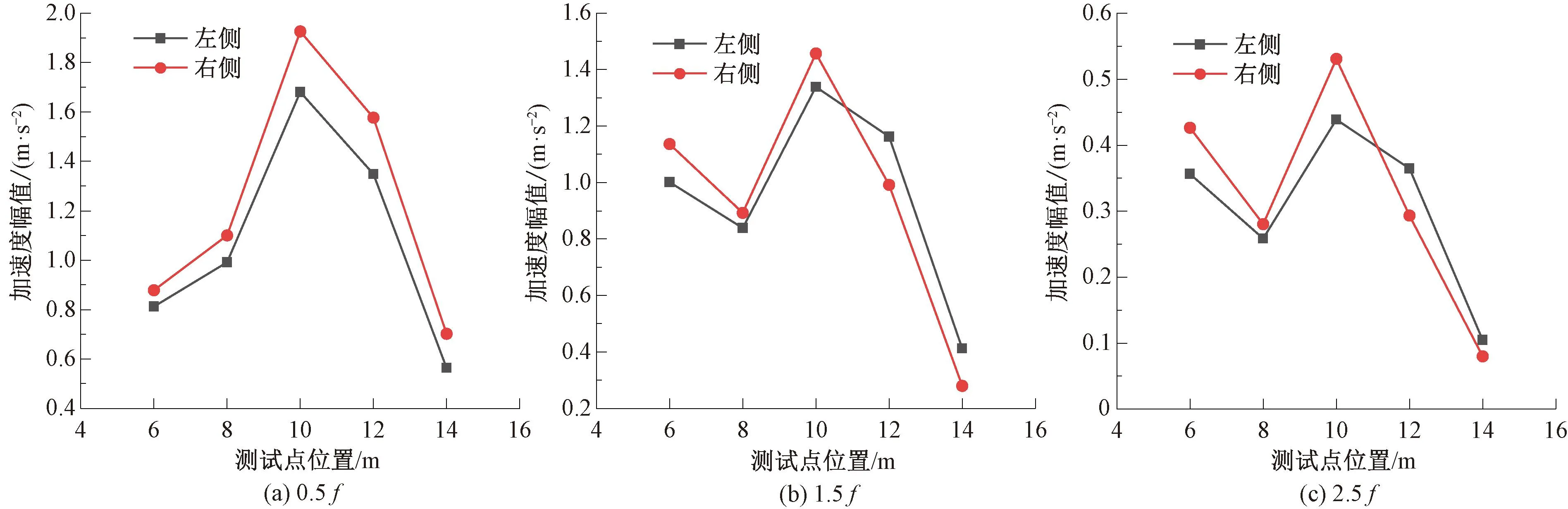
图12 振动轮两侧响应的非整数倍频幅值

综上,由CMV、CCV的定义可见,CMV为二倍频与基频的比值,CCV还包含了更多的非整数倍频。2个指标既体现了土体的非均质性,又包含了振动轮结构偏心特征,这是造成振动轮两侧连续压实指标差异非线性变化的主要原因。

2.4 优化指标检测适用性研究

为避免振动轮两侧响应差异对指标间相关性产生影响,以期提升连续压实指标对压实质量的测试精度。根据上文中谐波类指标差异产生机理,以不同谐波类型的连续压实指标为基础,构造以下3种指标,表征振动轮下土体的压实质量。

对振动轮两侧的CMV、CCV、AICV进行平均,分别得到双侧平均指标μCMV、μCCV、μAICV。其中AICV由1.0f、2.0f、3.0f频幅值组合计算得到[21],计算式为

( 7 )

根据计算的3种双侧平均指标,结合对应位置上的Evd,分析3种双侧平均指标与双侧Evd平均值的相关性,探究3种双侧平均指标能否用于质量控制。单、双侧连续压实指标平均值与双侧Evd平均值的相关性见图13。

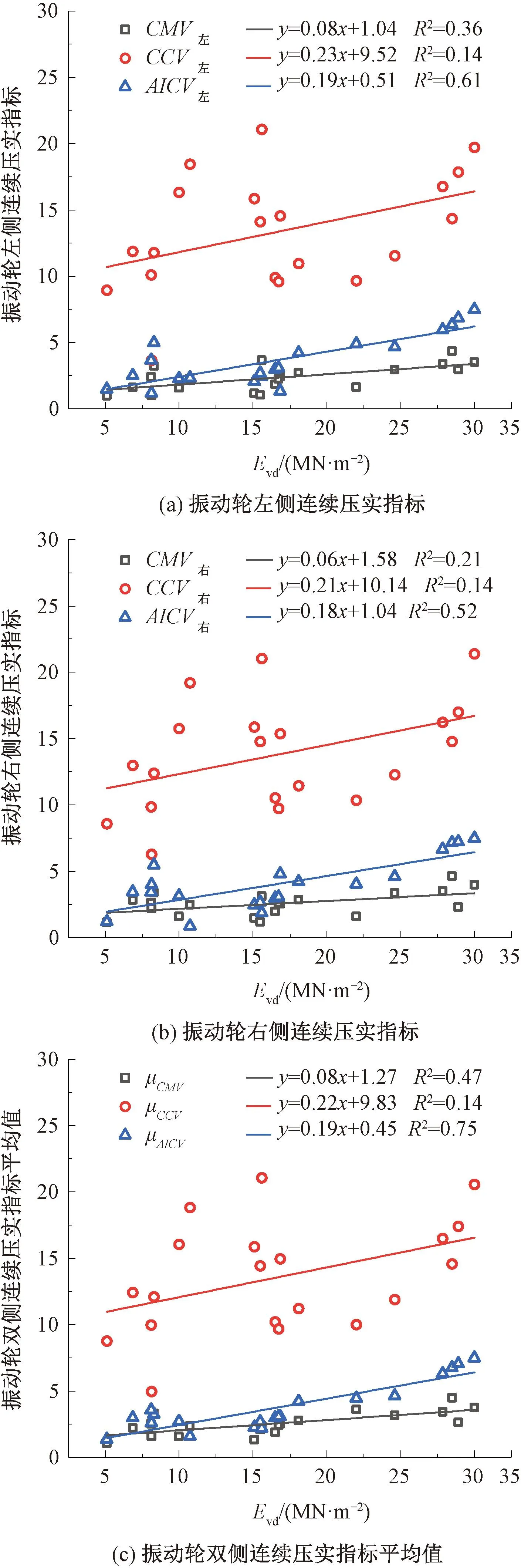
图13 单、双侧连续压实指标与双侧Evd平均值的相关性

由图13(a)、图13(b)可见,AICV与Evd的相关性要明显高于CMV与CCV,但其相关性均小于0.7,并不满足统计学上强相关的检验要求。意味着单侧指标用于质量检验存在误差。而从相关性排序来看,无论振动轮左右,CCV与Evd的相关系数均小于0.3,这表明CCV与检测指标基本不存在相关性,这主要是因为CCV包含了多个倍频,对碎石和粗砾石的压实评价具有更好的稳定性[20],本试验土体主要是粉质土,因此相关性较差。振动轮左侧的连续压实指标与Evd的相关性要略好于右侧,这是因为右侧为振动轮的驱动侧,会对振动轮右侧的响应产生一定影响,进而影响指标间相关性。

由图13(c)可见,μCMV、μCCV、μAICV与Evd的相关系数分别为0.47、0.14、0.75。其中μAICV与Evd的相关系数超过了0.7,意味着两者强相关,表明μAICV可以准确表征轮下土体的压实状态。其原因在于指标的定义,AICV包含了整数倍频,并未考虑非整数倍频,根据2.3节的结论,AICV的定义减弱了振动轮结构偏心的影响,加重了土体差异影响的权重。因此,其与Evd相关性更高。

相较于单侧,双侧连续压实指标平均值与Evd的相关性有所提高,进一步说明了双侧连续压实指标平均值在压实质量检测方面具有更好的适用性。