桥上CRTSⅠ型双块式无砟轨道早期开裂行为研究

2024-03-30李秋义黄庭杰左胜浩黄志斌

铁道学报 2024年3期

张凯，元强，李秋义，黄庭杰，左胜浩，黄志斌

(1.中南大学土木工程学院，湖南长沙 410075；2.中南大学高速铁路建造技术国家工程研究中心，湖南长沙 410075；3.中铁第四勘察设计院集团有限公司，湖北武汉 430063；4.东南沿海铁路福建有限责任公司，福建福州 350001)

传统有砟轨道存在轨道结构稳定性差、耐久性不良和列车高速运营安全性较低等不足。为此,双块式无砟轨道应运而生。双块式无砟轨道以其整体性良好、结构稳定和便于养护等优势,一经推出,便得到人们的广泛关注,且已成为我国高速铁路(以下简称“高铁”)轨道的主要结构形式之一[1-2]。然而,作为长大层状结构,在混凝土早期水化放热与收缩等因素影响下,双块式无砟轨道不可避免地出现各类伤损,进而导致轨道内部钢筋的锈蚀与结构耐久性的退化,且已成为制约双块式无砟轨道设计施工、影响高铁长期安全高效运营的关键科学问题之一[3-4]。

对于混凝土类材料,其早期凝结硬化过程为影响材料开裂行为的关键阶段[5]。迄今,国内外学者已围绕混凝土部件早期温度场演变机制、材料力学性能发展机制和材料早期变形规律展开系列试验与理论研究,并给出多种混凝土水化放热、收缩、强度、弹性模量等特征参数动态预测模型。同时,为探明大体积混凝土早期开裂机制,部分学者利用上述动态预测模型,基于数值模拟分析方法,对大体积混凝土部件早期温度场与应力场展开建模分析,并阐明混凝土早期开裂机理与因素影响机制[6]。

另一方面,为探明桥上CRTSⅠ型双块式无砟轨道早期特性,国内外学者围绕其早期温度场演变开展系列模拟,并初步确定无砟道床早期温度场演化机制[7],但早期变形与开裂行为仍不清晰。鉴于此,本文基于数值模拟分析方法,考虑轨道混凝土早期温度变形与收缩等影响,结合桥上CRTSⅠ型双块式无砟轨道结构特点,引入混凝土早期水化放热、收缩、混凝土抗拉强度、弹性模量、比热容等参数动态预测模型,考虑养护方法、拆模温度、拆模龄期和钢筋直径等参数影响,构建双块式无砟轨道三维实体模型,对CRTSⅠ型双块式无砟轨道早期温度与应力演变特征展开研究,以期为高铁双块式无砟轨道早期伤损抑制提供设计与理论参考。

1 混凝土早期性能演变特性理论

1.1 混凝土成熟度与水化温升模型

混凝土部件各项早期性能指标伴随水泥水化的进行而不断改变。同时,水泥与水的放热反应导致的温度升高以及周围环境(包括日常循环)的温度变化亦对混凝土各项早期性能影响较大。经历时间t时混凝土水化程度α(t)[8-9]为

( 1 )

式中:Q(t)为t时间段内混凝土水化放热量,kJ/kg;Qu为混凝土最终水化放热量,kJ/kg。

若水化过程中混凝土比热容保持恒定,则混凝土早期绝热温升与水化放热量应满足[8-9]

Q(t)=cθ(t)

( 2 )

式中:c为混凝土比热容,kJ/(kg·℃);θ(t)为养护龄期为t时混凝土绝热温升,℃。

则混凝土水化度可简化表达为

( 3 )

式中:θu为混凝土最终水化温度增量,℃。

另一方面,混凝土在任意时刻的水化速率与养护温度超出基准温度的累积之和成正比。为此,考虑温度对水化速率的影响,轨道混凝土等效龄期成熟度可基于下式[13]确定

( 4 )

式中:te为参考养护温度下的等效龄期,d;t为龄期,d;Tr为参考温度,一般取20 ℃;T为时间间隔dt内,考虑混凝土水化升温效应后混凝土内部的平均温度,℃;Ea、R均为常数。

基于混凝土等效龄期计算模型,国内外学者围绕混凝土水化度与等效龄期间的相关性展开进一步研究,并给出多种关系模型,较典型[8-9]的为

α(te)=αu(1-e-ξte)

( 5 )

式中:αu为混凝土最终水化度;ξ为常数。

1.2 混凝土早期性能演变机制

研究表明:伴随水化的不断进行,混凝土比热容与热膨胀系数均呈降低趋势。对于传统混凝土,其比热容与热膨胀系数[8-9]分别为

c(α)=c0(1.15-0.15α)

( 6 )

k(α)=k0(1.15-0.15α)

( 7 )

式中:c(α)与c0分别为混凝土水化度为α时及硬化混凝土的比热容特征值,kJ/(kg·℃);k(α)与k0分别为混凝土水化度为α时及硬化混凝土的线膨胀系数特征值,W/(m·℃)。

对于无砟轨道混凝土,混凝土弹性模量、强度等参数对其早期开裂风险影响较为显著。上述特征参数受等效养护龄期等因素影响较大,混凝土早期弹性模量[14]为

( 8 )

式中:Et(te)为等效龄期为te时混凝土弹性模量,MPa;Et28为养护龄期为28 d时混凝土弹性模量特征值,MPa;ts为龄期参数,d;s为受水泥种类影响较大的参数,对于波特兰水泥与快硬水泥,s=0.25,对于快硬高强水泥,s=0.2;n、E为由试验确定的常数。

混凝土早期抗压强度[8]为

fc(te)=[Et(te)/5 000]2

( 9 )

此外,混凝土抗压与抗拉强度间的关系[14]为

ft(t)=0.395[fc(t)]0.55

(10)

式中:fc(t)、ft(t)分别为养护龄期为t时混凝土抗拉、抗压强度,MPa。

对于水泥基类材料,其早期泊松比变化较小,由此,可取泊松比为0.20进行分析计算。

1.3 无砟轨道热传导边界条件

既有研究表明,温度场计算中,存在4类不同边界条件: ①混凝土表面温度为与时间相关的函数; ②混凝土表面热流量为与时间相关的函数; ③对流边界条件; ④混凝土与固体接触。对于双块式无砟轨道,道床混凝土浇筑完成后可认为现浇混凝土与底座板、轨枕等固体接触良好,满足第④类边界条件,并认为界面处热流量与温度连续。但对于暴露于空气中的混凝土表面与模板裹覆处,宜基于第③类边界条件表征混凝土内部与空气间热量与温度传导机制。其中,对于暴露于空气的界面,混凝土表面热流密度经验公式[9]为

(11)

式中:hfree为自由面处混凝土与空气间热流密度,W/(m2·℃);v为风速,m/s。

若无砟道床混凝土模板尚未拆除或上部采取养护措施,则混凝土与空气间热流密度[9]为

而项襄毅公者，尝抚陕擒叛酋俘馘万计，有大功。及入朝首率六卿暴阉宦汪直所任韦瑛罪，有奇节，而项大夫实继之。项先世洛人，其始祖宏度扈宋南跸徙嘉善，宏度生伯通，伯通生达卿，以散财广赈元世，尝复其家，赵文敏因表其墓。达卿生永原，永原生邦，邦为吴江丞，徙秀水而项遂为秀水人。邦生衡，两世皆以襄毅贵赠都察院左都御史。而赠都御史衡者，襄毅公之父，大夫之高祖也。[3]4391

(12)

式中:hi为第i层模板/养护包裹材料影响的混凝土与空气间热流密度,W/(m2·℃);li为第i层模板/养护材料厚度,m;ki为第i层模板/养护材料的导热系数。本文中,模板/养护材料厚度及导热系数取值见表1。

表1 模板/养护材料厚度及导热系数取值

受太阳辐照等因素影响,大气温度日变化规律极为复杂。本文模拟不同时刻大气温度演变规律的经验式[15]为

(13)

式中:Tair(t)为t时刻大气温度,℃;Tair为当地大气温度均值,本次模拟中,以长沙八月大气温度均值为例,Tair=30 ℃;tTmin和tTmax分别为当日内大气温度最低值与最高值出现时刻,对于长沙地区,分别为06:00与14:00;AT为日温差均值,对于长沙地区,取7 ℃。

1.4 无砟轨道混凝土早期变形

受内部与环境温度、湿度变化影响,混凝土凝结硬化早期通常伴随较大体积变形。对于普通混凝土,其早期变形包括自收缩、干缩和温度变形等,则混凝土早期总应变[16-17]为

εtot=εther+εas+εsh

(14)

式中:εtot为混凝土早期总变形量;εther为混凝土早期温度变形;εas为混凝土早期自收缩量;εsh为混凝土早期干燥收缩量。

自收缩为密封养护条件下混凝土表观体积减少的现象。对于普通混凝土,自收缩确定方法为[10]

(15)

εas(t,20)=2εas,28β(t)

(16)

εas,28=-3 070e-18.25

(17)

(18)

式中:εas(t,T)为养护温度为T、养护龄期为t时混凝土自收缩量;Tc为养护温度,℃;εas,28为20 ℃养护环境下混凝土28 d自收缩值。

干燥收缩为外部环境湿度低于混凝土内部,进而引起混凝土内部水分蒸发而引起表观体积减少的现象,其计算式为[16]

εsh=-1.2KvsKhsKfKtdεu

(19)

(20)

Khs=2-0.014H

(21)

(22)

(23)

式中:εu为28 d混凝土干缩量,εu=4.8 μm/m;V为混凝土体积,m3;S为内外接触面积,m2;H为相对湿度;tc为混凝土成熟度,d;fci′为加载初期混凝土无侧限抗压强度特征值,MPa,可取fci′=0.8fc。

温度变形为由于环境温度变化与水泥水化放热等引起的混凝土体积“热胀冷缩”的变形。混凝土早期温度变形[18-19]为

εther=ΔTαc

(24)

ΔT=T(t)-Ttime-zero

(25)

式中:αc为混凝土的热膨胀系数;ΔT为混凝土内部温度改变量,℃;T(t)为t时混凝土内部温度,℃;Ttime-zero为混凝土初始温度,℃。

2 模型建立与验证

2.1 模型建立

考虑轨道结构实际,基于混凝土温度场与应力场计算基本理论,通过有限元软件Ansys,以桥上CRTSⅠ型双块式无砟轨道(尺寸为6.4 m×2.8 m)为模拟对象,建立双块式无砟轨道温度场与应力场三维分析模型,见图1。假定道床混凝土与钢筋、底座板混凝土变形协调,即相同位置处道床混凝土与钢筋、底座板混凝土共用同一节点。同时,于底座板下部添加固定约束以模拟轨道下部结构对轨道的约束。

图1 有限元模型示意

分别选用Solid70、Solid65单元模拟轨道混凝土温度与受力演化机制,并选用多线性等向强化(MISO)模型模拟其受压应力-应变关系。选用Link180单元模拟钢筋受力变形行为,基于双线性随动强化模型表征其受拉本构,模型参数计算方法见式( 1 )～式(25),参数选取准则见表2。

表2 温度、应力数值模拟计算参数特征值

2.2 模拟参数选取

基于双块式无砟轨道温度场与应力场计算模型,分别计算养护方法、拆模龄期、拆模温度(考虑未拆模部件12 h内道床板温度场无明显变化,由此以12 h内不同拆模龄期表征不同环境温度)及钢筋直径等因素影响下道床温度场与应力场演化规律,并围绕上述各因素对无砟轨道早期变形的影响展开理论研究。其中,各部件设计参数见表3。

表3 双块式无砟轨道早期开裂模拟参数

2.3 测点选取与开裂风险预测方法

基于所建立的数值模拟分析模型,分别于双块式无砟轨道表面布置3个温度测点与45个应力测点,测点选取方案见图2。其中,温度测点分别位于道床板顶部、底部与中部节点,应力测点分别布置于道床板顶部道床板与轨枕四角处。另一方面,基于前文所给混凝土早期抗拉强度预测表达式(式(10)),明确7 d内所选45个应力测点处主拉应力计算值超越混凝土极限抗拉强度的概率,并定义该超越概率为双块式无砟轨道早期开裂风险概率。

图2 测点布置示意

2.4 模型适用性验证

为验证上述数值模拟分析方法的适用性,参考文献[20]试验参数与结果,将数值模拟分析所得结果与试验结果作对比分析。道床板混凝土表面温度对比见图3。由图3可知,基于2.1节所给的数值模拟分析方法所得轨道板温度演化规律与文献试验结果吻合良好,理论计算值与试验值误差始终保持较低水平,且均未超过1 ℃。但在4:00—8:00时间段内,数值模拟分析所得结果与试验结果略有偏差,偏差原因分析:数值模拟所取环境温度为测试地区环境温度均值,其值与试验现场环境温度间存在差异,进而导致误差产生。综上,本文所建立的无砟轨道温度场计算模型可精确表征双块式无砟轨道温度场演化机制,适用于无砟轨道早期伤损演变预测研究。

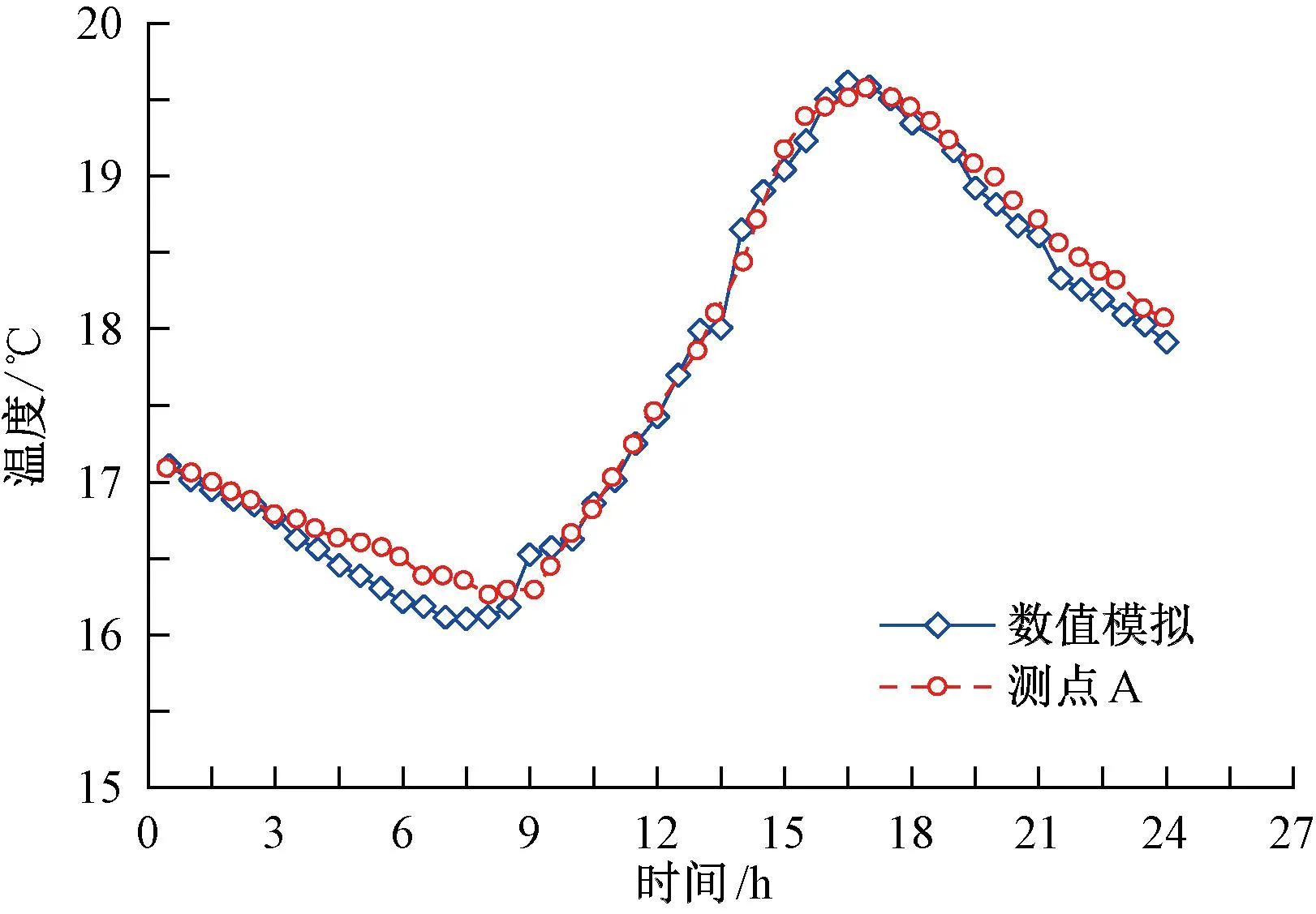
图3 道床板温度对比

3 计算结果分析

3.1 早期温度场演变分析

不同养护龄期下桥上CRTSⅠ型双块式无砟轨道混凝土早期温度场分布云图见图4。由图4可知,不同养护龄期下,双块式无砟轨道混凝土内部温度场分布规律并非一致。其中,当龄期为16 h时,轨道板内部温度分布规律为温度沿道床板由上至下逐步降低。原因分析:较短养护龄期条件下,水泥水化放热量较大,道床板底部混凝土与支承层混凝土温度场分布连续,且二者间可自由换热,故底部混凝土温度水平较低;对于上部混凝土,由于模板尚未拆除,混凝土与外部环境空气对流换热系数较小,进而导致轨道内温度水平沿高度呈递减趋势。另外,对于养护龄期较长的轨道板部件,道床混凝土温度场分布较为连续且温度水平低于养护龄期较短的部件。原因分析:对于养护龄期较长的部件,混凝土内水泥水化放热量逐步减少;同时,混凝土内早期存储的热量已逐步释放,故较长龄期的轨道混凝土部件内部温度场呈规律分布且温度水平较低。

图4 道床混凝土温度场分布云图(单位:℃)

桥上CRTSⅠ型双块式无砟轨道早期温度场典型时程曲线见图5。由图5可知,双块式无砟轨道早期温度场演变曲线可归纳为两部分:拆模前与拆模后。

图5 道床混凝土温度场时程曲线

1)拆模前:道床混凝土凝结硬化初期,伴随着水泥水化程度的不断加深,无砟道床内部水化放热量不断增加。由于裹覆模板尚未拆除,无砟轨道内外温度对流主要通过道床板顶面与双块式轨枕、底座板暴露面完成,内外温度对流幅度相对较小,进而使得温度-时间曲线近似呈线性增长趋势。之后,伴随着水化的进一步发展,混凝土内部水化放热速率逐步降低,其放热量逐渐等于或小于内外对流换热量,道床混凝土温度演化曲线不再增长或呈微降趋势发展。

2)拆模后:伴随着水泥水化的继续进行,待混凝土养护龄期增至拆模龄期后,新增水泥水化放热速率不断降低。同时,伴随着模板的拆除,无砟道床与外部环境的接触面积显著增大,拆模后4 h道床混凝土内部温度演化曲线出现明显的下降段。之后,伴随着龄期的增长,受环境温度等因素影响,混凝土内外热量交换量呈现循环衰减趋势,且每一循环温度峰值均较上一循环有一定幅度降低。

3.2 早期变形与应力演化分析

图6为道床板混凝土第一主应变分布特征。对于双块式无砟轨道,其峰值应变均位于道床板与轨枕四角,且应变云图在该位置近似呈八字形分布。同时,道床与轨枕接触界面处、轨枕四角连线区存在应力集中区,道床板内部混凝土应变较小。由此,双块式无砟轨道早期裂缝形态主要为轨枕四周离缝与轨枕斜向八字裂缝。

图6 道床混凝土应变分布云图

基于无砟道床混凝土应变分析结果,于双块式无砟轨道内部选取3个应力测点,并绘制其主拉应力与混凝土抗拉强度对比时程曲线,见图7。由图7可知:受外部环境与水泥水化程度等参数影响,无砟道床不同位置处混凝土主拉应力并非规律发展,但整体呈循环上升趋势。同时,伴随着养护时间的增加,道床混凝土主拉应力逐步达到或超越混凝土瞬时抗拉强度。此外,拆模前后混凝土应力时程曲线波动程度差异较大,且拆模后4 h内道床混凝土主拉应力时程曲线出现明显拐点,并呈现突变增长趋势。产生上述现象的原因应为:拆模改变了混凝土内外温度传导机制,导致道床内部温度场出现突变,进而使得道床混凝土主拉应力出现明显增大现象。

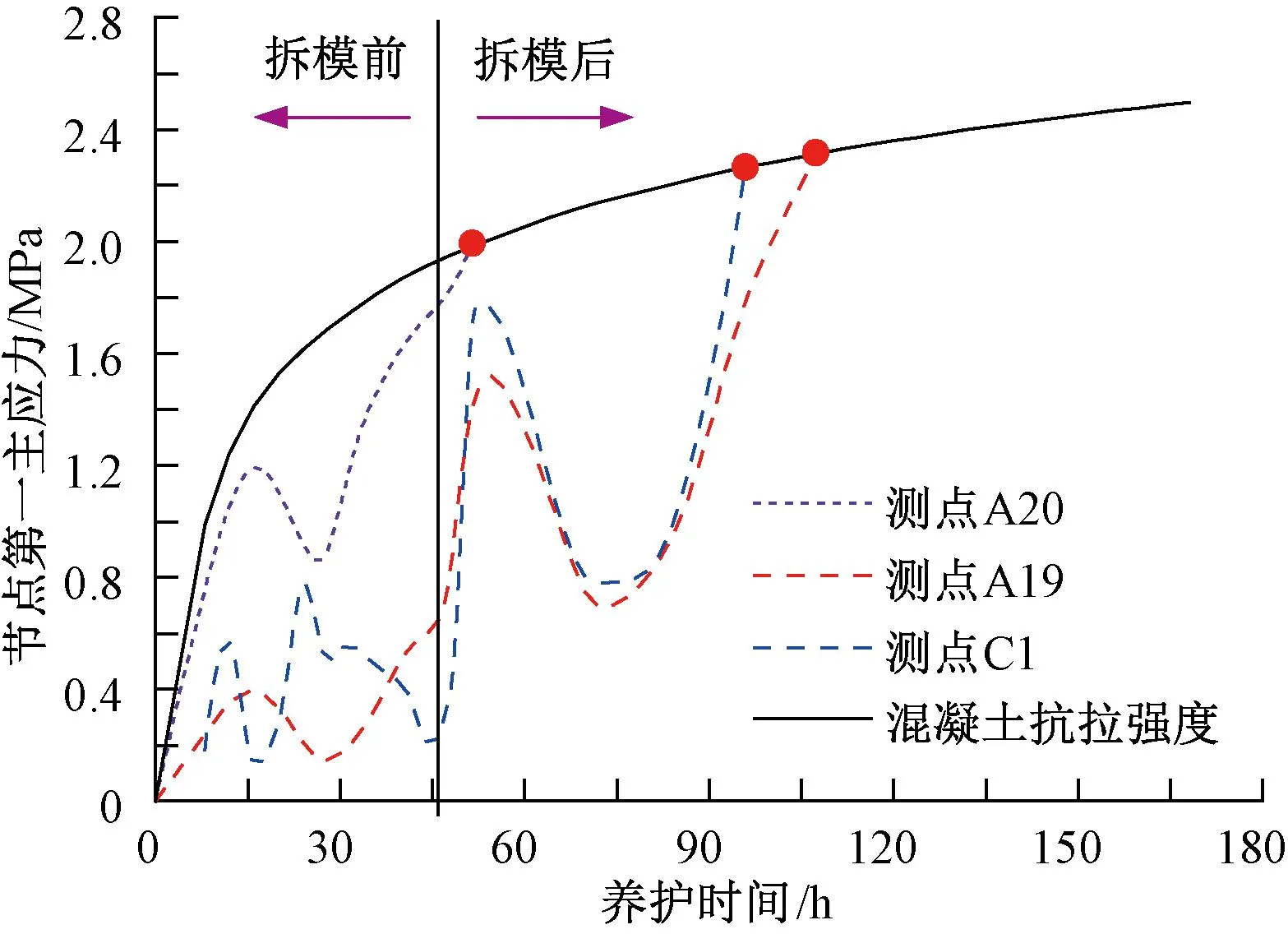
图7 道床混凝土主拉应力时程曲线

3.3 因素影响分析

1)早期养护方法

不同覆盖养护方法下道床板中部混凝土温度时程发展规律见图8。由图8可知,改变早期覆盖养护方法对道床内部温度场演变规律有较大影响。其中,养护方法为稻草浆板与土工布覆盖的部件,其早期温降程度远小于塑料薄膜覆盖部件。原因分析:相较于塑料薄膜覆盖养护方法(对流换热系数为14.25 W/(m2·K),土工布及稻草浆板覆盖的部件对流换热系数较小(分别为9.08、7.59 W/(m2·K),因而采用土工布及稻草浆板覆盖等养护方法的部件内外温度对流量较小。

图8 板内温度-养护方法关系曲线

双块式无砟道床早期开裂风险及其覆盖养护方式间的相关关系见图9。由图9可知,稻草浆板与土工布等散热密度较小的覆盖材料可显著降低道床板混凝土早期开裂风险,由此,施工中可选用内外热流传播密度较小的覆盖材料进行覆盖养护。

图9 道床开裂风险-养护方法关系

2)拆模龄期

无砟道床板顶温度演化规律与拆模龄期关系曲线见图10。由图10可知,各轨道板部件拆模前板顶温度时程演化规律类似,但拆模后各部件温度场发展规律存在较大差别。其中,108 h拆模部件4 h内温度改变量(5.52 ℃)仅为36 h拆模部件4 h内温度改变量(13.05 ℃)的42.3%。原因分析:养护早期,各部件均未拆模,其各项边界条件一致,故拆模前各部件温度场发展规律无明显差别;但伴随着养护龄期的增加,各部件相继拆模,且轨道混凝土拆模时的温度随拆模龄期的增大而降低,由此,各部件拆模后温度时程曲线差异较大,且表现为拆模龄期越小,拆模后4 h内道床混凝土温降越显著。

图10 板顶温度-拆模龄期关系曲线

双块式无砟轨道开裂风险与拆模时间关系见图11。由图11可知,无砟道床开裂风险与拆模时间呈现明显负相关关系。其中,当拆模时间由36 h增至108 h后,无砟道床开裂风险由37.78%降至17.78%,降低幅度达53%。出现上述现象原因分析:伴随着拆模龄期的增加,无砟道床拆模后温降值与波动幅度均呈下降趋势,故道床内部峰值温度应力与温度应力波动幅度随拆模龄期的增大而降低,由此,增大拆模龄期可降低无砟道床开裂风险。

图11 道床开裂风险-拆模龄期关系

3)拆模环境温度

无砟道床板顶温度演化规律与拆模环境温度关系曲线见图12。由图12可知,不同拆模温度部件拆模后4 h内温度变化量并非一致,且伴随着拆模温度的增加,道床板4 h温度改变量降低。其中,拆模温度为33.40 ℃的部件拆模后4 h内温度改变量(7.92 ℃)较拆模温度为27.25 ℃的部件(12.63 ℃)降低了约37.3%。原因分析:外部环境温度不同,道床混凝土与外部热量交换量存在差异,且随着内外环境温差的降低,内外换热幅度减少;又由于无砟道床早期温度高于外部环境,进而导致拆模温度较高的部件拆模后4 h内道床板顶部温度改变量较低。

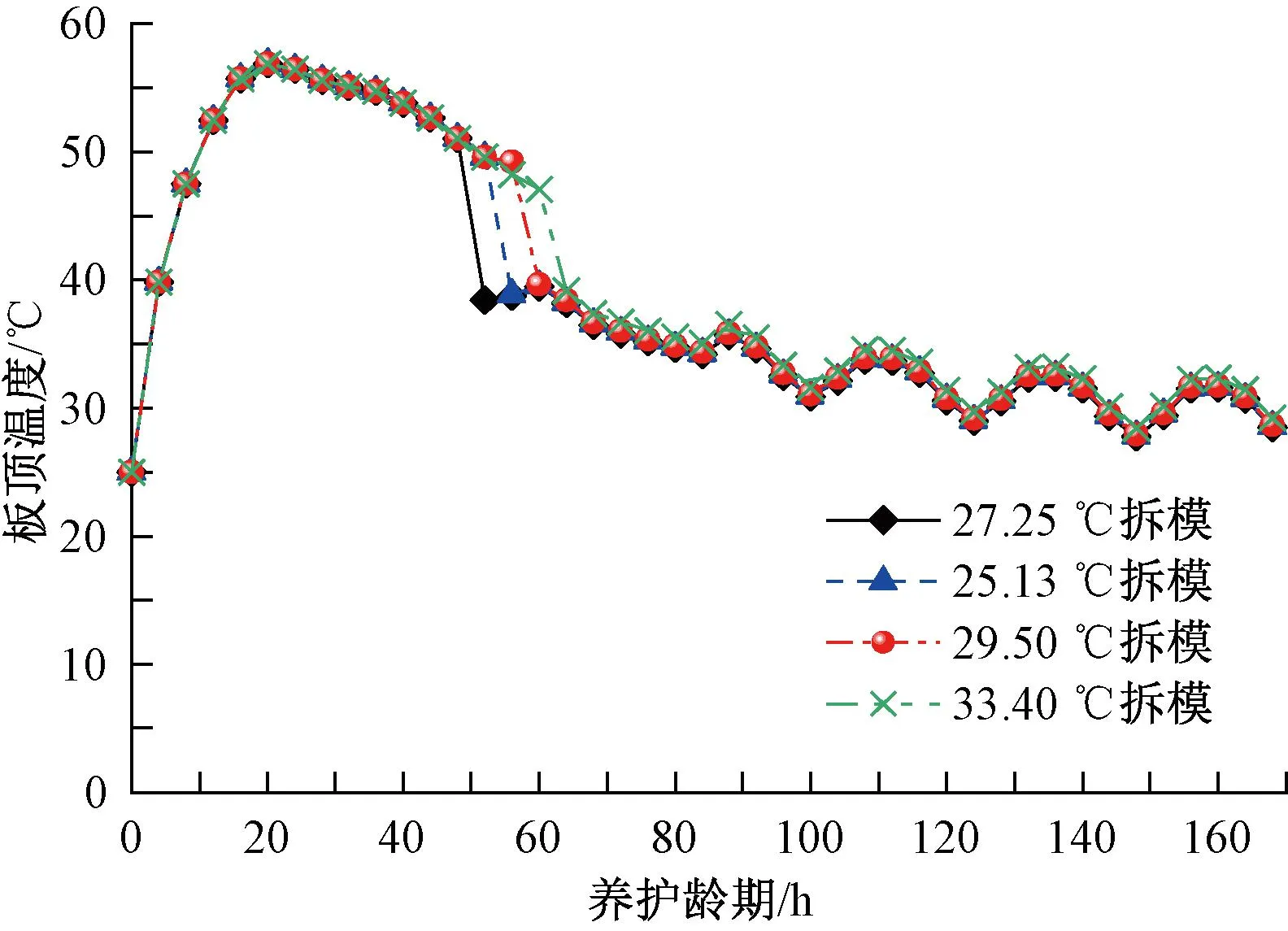
图12 板顶温度-拆模温度关系曲线

双块式无砟轨道开裂风险与拆模温度关系见图13。由图13可知,双块式无砟轨道早期开裂风险与拆模温度间存在一定相关性,且伴随着拆模温度的增加,无砟道床开裂风险整体呈降低趋势。其中,当拆模温度由27.25 ℃增至33.40 ℃后,无砟道床开裂风险降低了6.67%。原因分析:较高的拆模温度可改善拆模后道床温降程度,并进一步降低道床混凝土内应力增长幅度,故随着拆模温度的升高,道床混凝土开裂风险降低。

图13 道床开裂风险-拆模温度关系

4)钢筋直径

相同钢筋配筋率下,无砟道床板顶温度时程与钢筋直径关系曲线见图14。由图14可知,钢筋直径与道床混凝土温度场演变机制间无明显相关性。原因分析:①双块式无砟轨道中,钢筋体积远低于混凝土体积,进而导致钢筋直径对无砟道床温度扩散程度影响较小;②钢筋导热系数与混凝土接近,且无砟道床中二者接触面满足第④类边界条件(界面处热流量与温度连续)。由此,伴随着钢筋直径的改变,无砟道床混凝土温度场无显著变化。

图14 板顶温度-钢筋直径关系曲线

双块式无砟轨道随钢筋直径变化的开裂风险预测见图15。由图15可知,拆模前道床开裂风险与钢筋直径相关性不大,但拆模后随着钢筋直径的增加,无砟道床开裂风险增大。其中,钢筋直径为16 mm的道床板的总开裂风险(37.8%)较直径为8 mm的道床板(22.2%)增大达70%。原因分析:在相同配筋率情况下,钢筋与混凝土间的握裹面积随钢筋直径的增大而减少,对于早期混凝土,其弹性模量等物理参数远低于轨道内配筋,在温度与收缩变形等的影响下,大直径钢筋部件钢筋周围混凝土应力水平更高。综上所述,双块式无砟轨道的抗裂性能受钢筋直径影响较大,且当钢筋直径更小时轨道抗裂性能更优。因此,宜在合理范围内选用直径较小的钢筋作为轨道配筋。