高速铁路动检车轴箱加速度与轮轨力数据里程对齐研究

李王逸嘉，李晨钟，何 庆，王 平，杨 飞，吴维军

(1.西南交通大学 土木工程学院，四川 成都 610031；2.西南交通大学 高速铁路线路工程教育部重点实验室，四川 成都 610031；3.中国铁道科学研究院集团有限公司 基础设施检测研究所，北京 100081；4.南昌大学 机电工程学院，江西 南昌 330031)

保持高速铁路(以下简称“高铁”)的高平顺性对行车安全具有重要意义。在高铁工务运维工作中,开展定期的轨道动态检测是指导轨道养护维修工作的前提和基础[1]。轨道动态检测主要包括轨道几何与车辆各部件动态响应两个方面,其中轨道几何指标包括高低、水平、轨距、轨向、扭曲等,车辆动态响应指标包括车体垂向/横向振动加速度、轴箱垂向/横向振动加速度、轮轨作用力等。这些指标可以从轨面平整度、线型平顺性[2]、轨道弹性变形度及乘车舒适度等多个方面反应轨道的运营状态。

目前基于轨道几何的评价方法主要包括峰值扣分法和轨道质量指数法(track quality index,TQI)。前者仅关注超限点峰值与数量,难以反映轨道区段平均质量状态[3-4];TQI法关注评价区段所有测点的幅值,弥补了峰值扣分法的不足,但需要人工排除因电力、环境等因素造成的数据异常[5]。与此同时,受限于设备检测精度,两种方法均无法反映幅值极小的短波不平顺类型(例如微米级的波浪形磨耗)。

相比于轨道几何数据,轴箱加速度、轮轨力数据因其高频采样的特性可以更全面地反应轨道下部短波不平顺,弥补现有评价方法在短波不平顺检测中的不足。目前所使用的轮轨力数据一般通过测力轮对获取[6-7],但测力轮对造价昂贵且容易损坏。而轴箱作为测量点位相对稳定,轴箱加速度更易直接通过传感器跟车采集[8-10],所需费用较低且耐用性强。

为了减少测力轮对的使用,降低数据获取成本,国内外多位学者[11-14]正致力于使用轴箱加速度对轮轨力进行预测。目前,以物理公式推演或仿真实验所建立的映射关系难以表征列车在真实运营条件下的复杂情况,要确立实测轴箱加速度、轮轨力数据之间的映射关系,两种数据间高精度对齐的里程信息是重要前提。此外,运维部门通常掌握多种类型运维数据,可利用多源数据所携带的不同信息对数据本身进行印证和补充,例如在不平顺数据TQI值超限的位置是否出现对应的轴箱加速度、轮轨力峰值;在TQI值正常区段的轴箱加速度、轮轨力数据又是否出现能量集中现象,而利用多源数据对轨道状态进行综合评价同样建立在高精度对齐的里程信息的基础上。里程误差[15-16]的存在会使探索两种高频采样数据间的映射关系的难度大幅增加,也阻碍利用多源数据对轨道状态进行综合评价。因此消除不同数据间的里程误差对数据综合分析、确立映射关系都至关重要。

目前,在轨道领域的里程修正方法仅针对轨道几何数据,且两列数据通常为同类数据。当轨道几何数据存在明显曲线特征时,可以利用主点信息进行里程修正,如文献[17]利用曲线台账信息修正设备误差,建立相关系数五点迭代法逐段修正二次偏差;文献[18]提取直曲线交汇区域主点,基于相关系数法与二次插值将里程误差根据主点信息全局平均化进行修正,并根据数据窗长的敏感性分析对算法进行优化;与之类似的逐区段修正算法还有最小二乘法[19-20]、灰色关联度算法[21-22]等。此外,可以利用由焊缝引起的轨道几何峰值特征进行误差修正,如文献[23]建立三次样条插值模型提取高低不平顺数据中焊缝特征位置,将其规律性特征作为窗长选择的参考值,结合均一阈值和真实焊缝修正里程误差;文献[24]提取实测轨距与设计轨距数据间互相关峰值位置,利用自回归时间模型和卡尔曼滤波器修正历史数据里程误差。基于动态规划的思想,根据两波形之间最优匹配位置下各点最短距离路径也可以进行误差修正,如文献[25]采用动态规划(DP)算法,对二维曲线进行匹配修正。文献[26-28]提出在轨道不平顺数据中提取关键设备信息,结合动态规划原理建立两次检测数据间的最优配对模型,并以目前数据存在的最大里程误差的倍数作为匹配窗口长度的约束求解模型;文献[29-30]提出动态时间弯曲(DTW) 算法,以欧式距离为波形相似度度量计算最短弯曲路径,通过对横坐标时间轴的弯曲和变形进行里程修正。文献[31]将互相关函数、快速傅里叶变换递归对齐、相关优化弯曲及动态时间弯曲方法下的几何缺陷数据对齐效果进行对比,发现DTW在波形对齐时拥有最高的精度。

综上所述,目前的修正模型几乎仅适用于波形重复度高的同类型数据,鲜有学者对不同类型但相互关联的高频采样数据进行里程修正,现有研究对多源数据之间里程误差的处理仍存在以下不足:

1)部分逐区段里程修正算法需要将数据本身携带的曲线特征信息与线路台账相结合才能进行数据修正,但轴箱加速度与轮轨力数据并未携带曲线特征信息,无法直接通过该类模型进行修正。

2)在高采样频率下,数据整体或局部的里程误差将更多次积累,修正模型的整体运算量呈数量级形式大幅度增加,以动态规划思想进行波形修正的算法(如DP、DTW算法等)难以在庞大数据量下保持运算效率和精度,易出现波形过度变形,修正后波形失真的问题。

3)目前在铁路数据分析领域,对于描述两种高频采样数据对齐效果的量化评价方法尚存在研究空白。

基于以上研究的不足之处,本文利用窗长变化作为减小算量、提高算法精度的突破口,提出一种长、短单元窗长收敛的二阶段里程误差修正模型,针对缺乏曲线信息且高频采样的轴箱加速度、轮轨力数据进行修正对齐。算法的具体流程如下:

1)第一阶段,利用速度信息代替“曲线特征”建立轴箱加速度、轮轨力数据之间的联系,根据四分位数阈值界定原则提取长单元速度曲线趋势,并利用速度变化区间初步修正两种数据间波形错位,极大地减少了运算量,大幅提高第二阶段修正的运算效率与准确性。

2)第二阶段,为避免一次性处理大量数据所带来的波形失真问题,先对全局数据进行短单元分割,而后基于互相关匹配得到两种数据之间的精确里程修正矩阵,该矩阵基于贪心算法思想逐区段对原始数据进行线性插值,在保留数据真实性的同时消除两种数据间内部的里程残差。

3)为避免高频采样数据发散性、随机性的特点对幅值结果评价的影响,提出以“能量”的形式提取高频采样数据趋势,对加速度、轮轨力数据修正结果进行量化评价,将原始数据、粗匹配数据以及精确里程修正后数据之间的相关性进行对比分析。

1 数据说明

使用同一列车不同车厢上不同采集系统所采集的轴箱加速度与轮轨力数据,左轴箱垂向加速度、左轨垂力原始数据分别见表1、表2。其中,n为采样点数量。由表1、表2可知,轴箱加速度、轮轨力数据均按等时间间隔采样,但输出的数据中仅有里程、速度数据而缺乏时间标签,无法直接通过速度与时间的乘积得到距离进而对波形整体漂移进行修正。此外,在等时间间隔采样下,车辆速度一般通过里程计、光栅编码器、应答器得到。在长距离的行车中,由于车轮磨耗、轮轨间相对滑动、编码器故障等问题,很容易造成里程的累积误差。如果利用列车纵向加速度积分得到速度,会存在更大的积分误差,但由于本文数据跨度很长,以这种方式得到的距离在积分累积误差下可能会导致新的问题。

表1 左轴箱垂向加速度原始数据

表2 左轨垂力原始数据

相比于类型相同、检测系统一致的两次轨道几何数据间的里程误差修正,不同类型的两种数据之间的里程误差修正将更加复杂,需要解决的问题如下:

1)缺乏曲线特征点。通常来说,用于进行里程修正的不平顺数据多以超高、高低数据为主。超高指为抵消车辆在圆曲线路段上行驶时产生的离心力导致的滑移而设置的外侧高于内侧的单向横坡,因此在弯道位置,超高数据必然会呈现梯形状变化,不同时间段测得的两次超高监测数据可根据“直缓点”“缓圆点”等曲线特征点进行校准。然而轴箱加速度以及轮轨力数据趋向于随机分布,并不一定存在类似的数据特征点。

2)高频采样。通过轨检车得到的轨道不平顺数据通常以0.25 m或0.125 m进行等间距插值,属于低频数据。而轴箱加速度、轮轨力数据分别以5 000、2 000 Hz进行高频采样,在同样的行驶距离内得到的数据总量呈数量级形式增加。

3)数据类型差异。用于匹配的轨道几何数据往往为同类型数据,其采样频率、方式均相同,因此两次数据波形之间重复度往往很高。而当匹配数据变更为加速度与轮轨力数据时,其数据类型、采集方式、采样频率均不同,因此采集到的两种原始数据之间的波形匹配存在随机性,难以做到点与点之间的对齐。

综上所述,本文所处理的里程误差是在多种因素的共同影响下产生的。首先,两套采集系统位于同一列车的不同车厢,难以做到同时、同频采样,这是造成波形整体偏移的主要原因之一;其次,两套采集系统本身所使用的GNSS定位系统或光栅编码器也可能会导致里程误差的产生;最后,由于采集的系统、频率均不同,导致采集的数据内部存在拉伸或者压缩的现象,以上3种因素共同影响产生了里程误差。且由于采集系统的不同,两数据间的里程误差无法通过设备直接消除。若忽略该误差对原始数据进行修正,会出现计算量太大的问题。由于缺乏曲线信息,原始波形也难以展现两种数据之间的整体关系。

由表1、表2可知,两套采集系统所采集到的每一个加速度、轮轨力数据都存在与之对应的速度数据。相比于波动性极强的加速度、轮轨力数据,速度数据通常在行车过程中保持稳定,速度变化时所呈现出的波动会在整体数据中尤为明显,且其波形的重复性较高,因此,可以利用两套系统速度波形之间的偏移量来反映轴箱加速度与轮轨力数据之间的整体偏移量。在消除波形错位之后,再对轴箱加速度、轮轨力数据进行局部波形的收缩、拉伸处理,逐区段消除全局里程误差。

2 基于长、短单元窗长收敛的二阶段里程误差修正模型

本文所提出模型在第一阶段将轴箱加速度与轮轨力两套采集系统中的速度数据作为里程位置参考,通过四分位数阈值界定提取速度变化长单元区段,基于长单元速度窗消除两种高频采样数据间整体里程误差。在高速列车行驶过程中,速度不断发生波动,但通常波动范围仅1～2 km/h,依靠四分位数法可以将速度大幅度变化区间与细小波动分离开,这种大幅波动区间在240 km/h的速度下通常会长达2 km,因此称之为长单元。在第二阶段,以轮轨力数据为基准,对轴箱加速度数据进行短单元分割,再根据互相关匹配法修正每个短单元内轴箱加速度数据,最后通过线性插值对轴箱加速度波形内部各区段进行伸缩与拼接处理,逐区段消除残余的里程误差。短单元的长度至少应大于轴箱加速度的一个采样周期且包含2～5个焊缝冲击信号在内,在240 km/h的速度下短单元长度约为150～300 m,里程误差修正模型流程见图1。图1中,i为当前轴箱加速度窗口数;j为当前轮轨力窗口数;jmax为最大轮轨力窗口数。

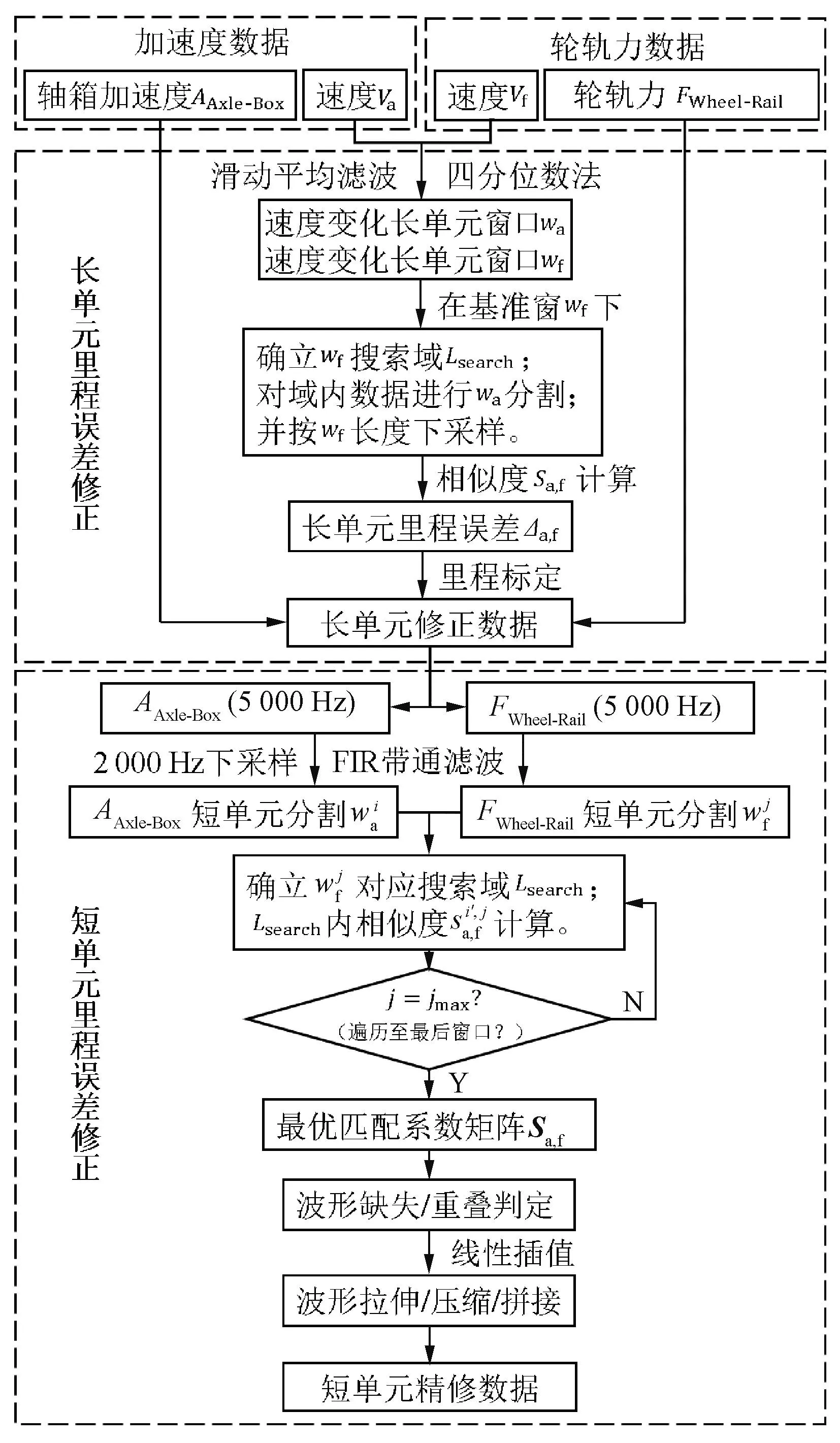
图1 里程误差模型示意

2.1 长单元里程误差修正方法

四分位数阈值界定法用上、下四分位数和四分位差来定义内限、外限,将内限以外的小概率离群点视为异常值。利用上、下四分位数(总体数据从小到大排列后位于75%与25%位置的数据)Q3和Q1以及四分位差QIQR(Q3-Q1)来确定内限,内限范围为(Q1-1.5QIQR,Q3+1.5QIQR),数据点落于内限以外的概率为0.7%,可视为小概率离群点,本文将此类数据作为速度变化区间。可根据需要,对所需QIQR的倍数阈值进行调整,从而将变化区间与细微波动分离。

图2 长单元里程误差修正方法

在相似性评价计算时,需保证数据长度与形式一致,为保证变化后数据的真实性,将采样频率相对较低的轮轨力数据作为基准数据。按以下步骤修正长单元里程误差。

1)基准窗口选取

将Vf数据变化区间,即轮轨力速度数据Vf与轮轨力四分位限值切割区间wf作为基准窗口,窗长为lf。

2)加速度-速度数据窗口分割

以窗长la对Va数据进行矩形窗分割处理。为保证波形之间具有更好的重复性以及相似度评价的准确性,窗与窗之间的间隔不宜过大,建议步长约为窗长的千分之一。

3)基于基准窗口长度的Va窗口数据下采样

Wa={wai|i=1,2,…,n}

( 1 )

式中:ca为相邻窗口间步长;int(·)为取整函数。

4)搜索域波形相似度计算

以基准窗口的中心里程Mf为中心,在加速度的速度数据Va中提取里程点Mf前后3倍波峰或波谷间极值点差的里程区段作为搜索域Lsearch,计算整个搜索域内加速度窗口集合相对于轮轨力基准窗口内速度波形的相似度sa,f,得到波形相似度向量Sa,f。

Lsearch=(Mf-3lcrest,Mf+3lcrest)

( 2 )

( 3 )

( 4 )

( 5 )

5)确定最优匹配窗口中心里程

将波形相似度向量Sa,f中皮尔逊相关系数最大值位置所在窗口认定为最优匹配窗口,并以此得到匹配窗口中心位置里程Ma。

6)波形错位里程重新标定

Δa,f=Mf-Ma

( 6 )

( 7 )

2.2 短单元里程误差修正方法

通过长单元的里程标定修正后,原始数据波形的整体错位被消除,但长单元修正并未解决数据波形局部不均匀分布的问题。因此,按以下步骤对高频采样的轴箱加速度、轮轨力数据中短单元里程误差进行修正:

1)基于轮轨力基准数据采样频率的加速度数据下采样与窗口划分

在对两种波形进行相似度计算时,需确保窗长内两种数据采样点数量一致,因此以基准数据的采样频率fs,对加速度数据进行下采样,得到的加速度采样点为Na,基准数据的采样点Nf不变。

2)加速度、轮轨力数据窗口分割

第一课时教学中，主要以人物年谱表为教学的“抓手”，让学生在阅读、勾画、填表中自主学习，学生在与文本、海伦、教师充分地对话之后，发现人物小传写作的两大密匙：按时间节点写清人生轨迹；详写一些经历，突出人物特点。

( 8 )

( 9 )

3)搜索域判定

Ls,search=

(10)

4)计算以轮轨力数据窗口为基准的遍历相似度评价矩阵

(11)

(12)

(13)

5)确定最优波形匹配矩阵

(14)

(15)

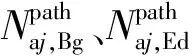
6)多次插值的短单元波形伸缩修正方法

表3 波形重叠与缺失情况表

若忽略掉区段的重叠与缺失部分,直接将匹配窗口数据进行拼接将会导致轴箱加速度波形的重复与失真,因此在数据拼接前应将缺失、重叠部分考虑在内,对加速度数据窗口进行插值伸缩,线性插值函数为

(16)

式中:xi、yi分别为原数据曲线第i点的横坐标和原数据曲线函数值;xi+1、yi+1分别为原数据曲线第i+1点的横坐标和原数据曲线函数值;xnew为数据曲线插值点横坐标;ynew即xnew下数据曲线函数值。

判定与线性插值修正过程如下:

图3 里程误差线性插值修正方法

对加速度数据相邻窗口进行判定规则如下:

(17)

(18)

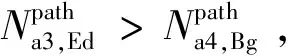
(19)

重复上述过程直至所有的匹配窗口全部转化为修正窗口,再进行拼接形成里程误差修正之后的轴箱加速度数据。

3 实例验证

为验证里程修正模型的有效性,选取某双向东部货运专线里程K80+000—K140+000区段的轴箱加速度、轮轨力数据进行分析。本节基于选取的数据分别进行长单元初步修正、短单元精确修正,并展示每一步修正前后的结果,最后对修正前后结果进行量化对比。

3.1 工程实例

在第一阶段,用速度数据建立轴箱加速度、轮轨力数据之间的联系,进行长单元里程修正。为提取速度波形,使用FIR滤波器进行0.1 Hz低通滤波去除原始高频采样产生的毛刺,再对滤波后的数据进行滑动平均处理,处理后速度数据频数分布见图4。由图4可知,速度数据呈现“非正态分布”的特征。

图4 加速度、轮轨力数据速度波形及分布

为将速度细微波动与速度变化区间分离,以Q1～2QIQR为界限对原始数据进行分割,将Q1～2QIQR范围之外的区段视为速度变化的区间,并对速度变化的闭合区域进行提取,见图5。

图5 四分位阈值界定判定速度变化区间原理

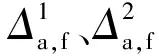
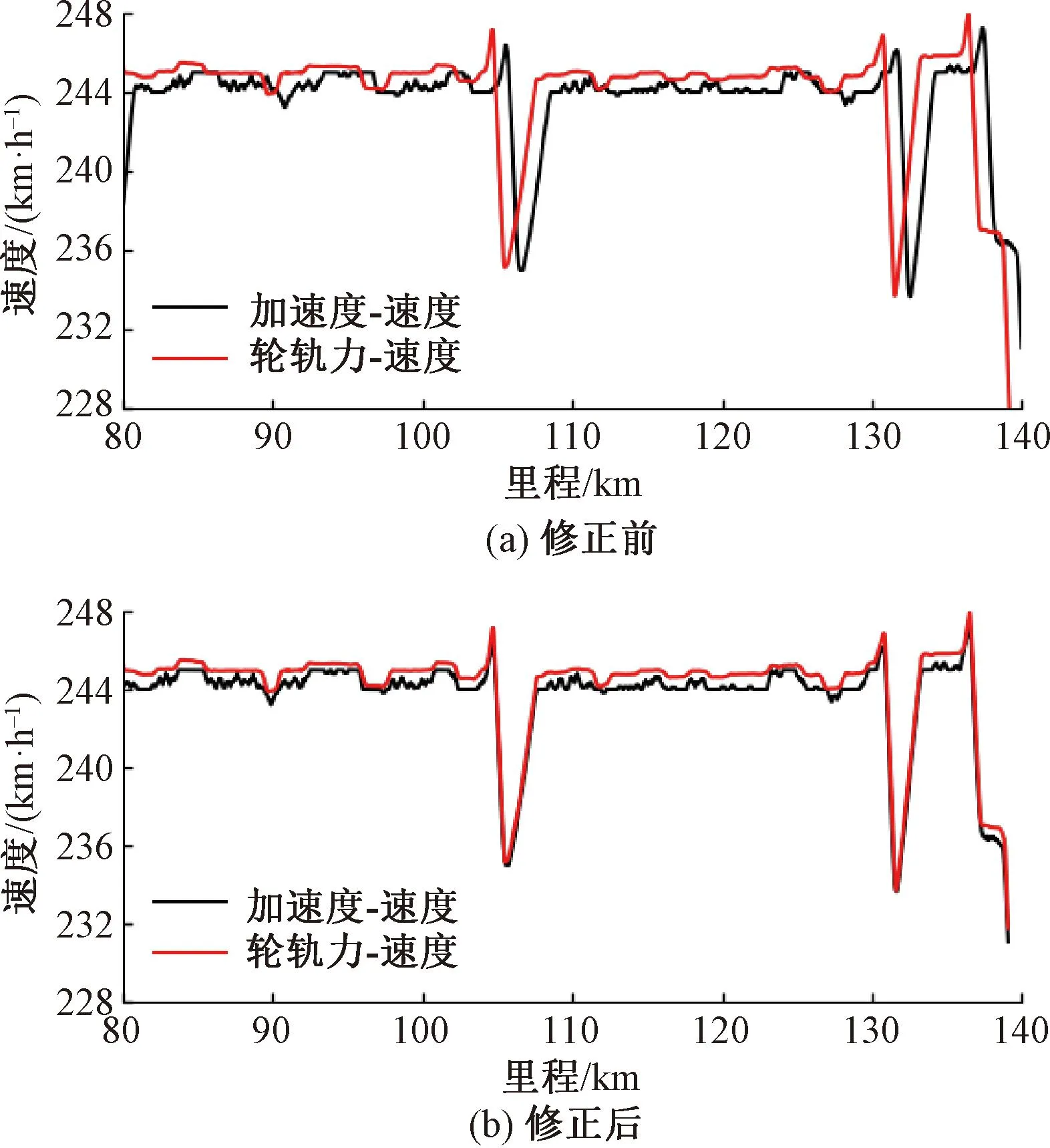
图6 长单元修正前后速度图像对比

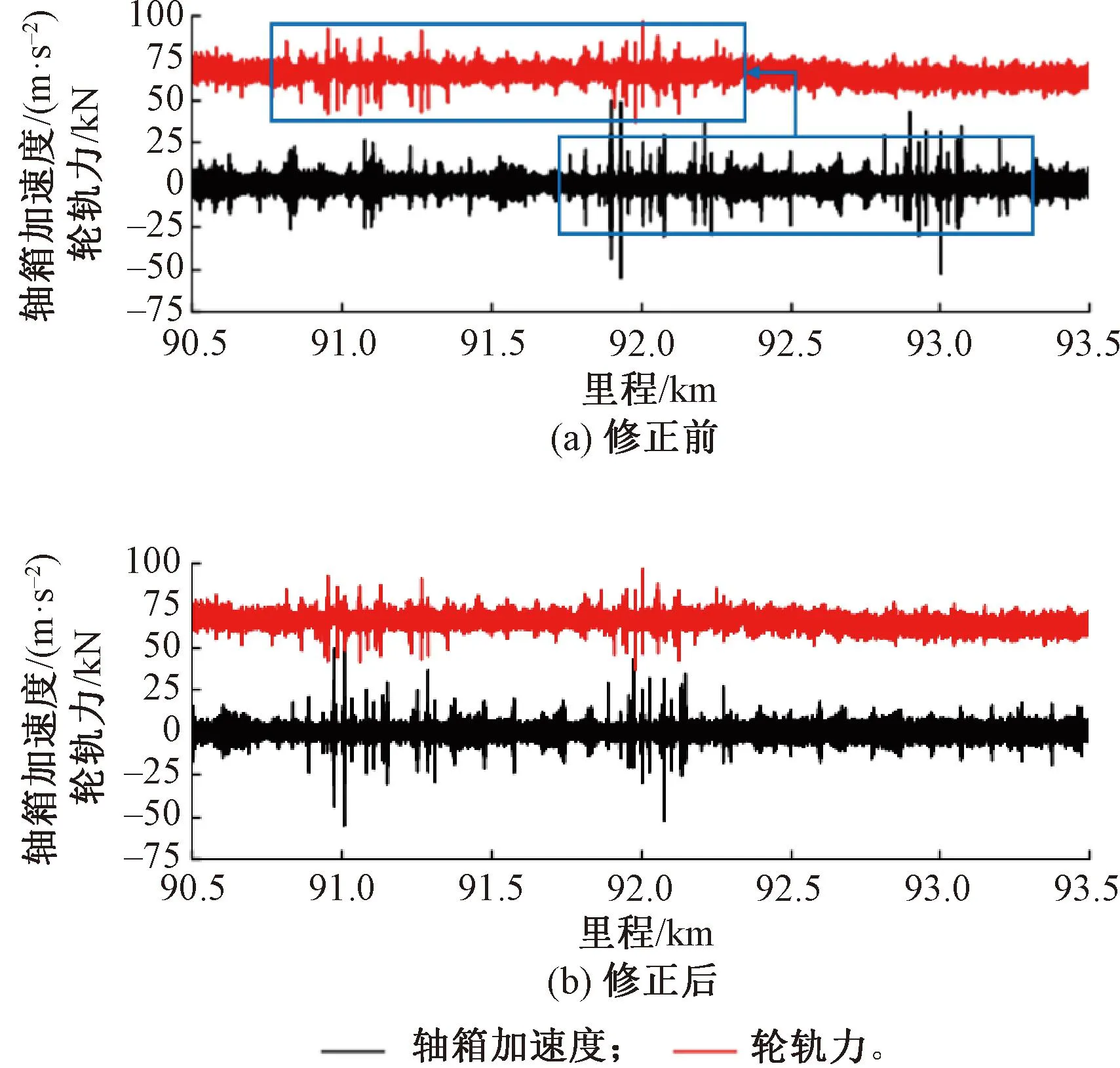
图7 长单元修正前后轴箱加速度、轮轨力数据

轴箱加速度、轮轨力区段长单元修正前后数据见图8。这种以长单元区间的平均误差对整体数据进行波形平移修正的方法仍存在以下缺陷:①不能处理长单元内部的里程误差信息;②里程误差存在于整个修正区段内且非均匀分布,平移并不能解决两种数据波形整体或局部的收缩、拉伸问题。前后相差近0.07 km的Δa,f表明,原始数据内部仍存在由波形伸缩造成的里程误差,因此需要对高频加速度、轮轨力数据进行短单元精确里程修正。

图8 短单元修正前后轴箱加速度、轮轨力数据

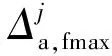
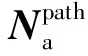
在经过第一阶段的长单元修正后,两数据任意区间相对里程误差从1 km缩小至42 m以内;而后在经过短单元精确修正后,各区段里程误差均值为0.32 m,在99.7%的置信度下,该线路任意区段高频采样数据误差可控制在[-0.92,1.55]m。

3.2 与DTW修正效果的对比

文献[31]已将互相关函数、快速傅里叶变换递归对齐、相关优化弯曲及动态时间弯曲方法下的几何缺陷数据对齐效果进行对比,发现DTW算法在波形对齐时拥有最高的精度。因此此处将DTW算法的运行结果与本文方法进行对比。

DTW算法的修正方式见图9,在每一步中都需要计算与之相邻点的累积距离,并根据最短累计距离选择最优匹配路径。但由于本文数据量异常庞大,该累计距离矩阵将会特别冗长,再加上两种数据具备峰值随机出现的特点,因此在修正效率上,利用DTW算法对原数据进行修正的时间较长,接近3 h,而本文提出的二阶段收敛窗长下的用时仅为DTW算法的六分之一。

图9 DTW算法的运作模式及累计距离矩阵

由于DTW算法会对数据的时间轴进行弯曲来对数据进行修正,因而当数据量较大时,很容易出现由于过度的拉伸、压缩而出现的波形失真。在此随机截取一段原始数据、经本文二阶段窗长收敛算法修正后数据与DTW算法修正后的数据进行对比,见图10。由图10可知,DTW算法修正后的轴箱加速度数据出现了严重的波形失真,而本文所提出的方法可以很好地保证数据的完整性和真实性。对该段两种算法修正结果以皮尔逊相关系数进行衡量发现,本文所提出二阶段窗长收敛修正算法较DTW算法的皮尔逊相关系数提升了约5倍。

图10 二阶段窗长收敛法与DTW算法修正结果对比

3.3 基于能量累积趋势的线性相关性评价

依据高频采样数据单个峰值评价存在随机性、发散性的问题[32],但轨道高频振动下的冲击能量却相对稳定,均方根值具有“能量”的概念,可用于度量轨道短波不平顺引起的动态响应。轴箱加速度、轮轨力数据作为高频采样数据,对轨道短波不平顺产生的高频信号非常敏感,相对于点对点的峰值相似性评价,利用滑动积分窗内均方根值提取修正后的两种数据区段能量趋势的变化,通过对该趋势的相似性评价来对修正效果进行衡量将更加合理。

首先对轴箱加速度、轮轨力进行数据标准化,消除数据量纲的影响,逐步计算所有数据,并分析单元内均方根值Si。

(20)

(21)

在完成均方根计算后,提取两种数据每5 s内50个分析单元的均方根能量趋势,进行相似度评价,结果见图11。

图11 修正前后高频采样数据能量趋势评价对比

由图11可知,两种数据的整体能量趋势线性相关性系数从-0.079提升至0.650,且红色曲线所代表的精确修正数据几乎在全局任意区段均优于原始数据,表明修正模型提高了两种数据之间的整体相关性。其中红色曲线的极值下降点部位原始数据波动不明显,线性相关性较低,结合台账数据与超高数据对比,暂排除其与弯道、桥梁段之间有直接关系,有待进一步研究。

4 结论

针对高铁动检数据中轴箱加速度和轮轨力数据提出基于二阶段波形匹配的里程对齐算法,在减小里程误差方面取得良好的效果。主要结论如下:

1)利用速度数据代替“曲线特征信息”建立高频采样数据之间的联系,通过识别速度变化区间消除因采集系统不同导致的长里程偏移,有效提高计算效率,并提出一种全局里程插值修正方法,在避免修正过程中出现波形失真的同时保留了修正数据的真实性。

2)通过两阶段修正模型处理轴箱加速度、轮轨力数据里程误差,在长单元修正后,两数据任意区间相对里程误差从1 km缩小至42 m以内;经过短单元精确修正后的两种数据在99.7%的置信度下任意区段间的里程误差可控制在[-0.92,1.55]m。

3)从“能量”的角度提出一种高频冲击数据修正前后的量化评价方法,在此方法下,原始的轴箱加速度、轮轨力数据间相关系数仅有0.07且为负相关,经过二阶段修正后整体数据间相关系数达到0.65,两高频采样数据间的相关性得到显著提升。

综上,模型将原高频采样数据间近1 km且分布不均的里程误差缩小到1.55 m以内,为探究实测轴箱加速度、轮轨力之间映射关系提供基础,对研究轨道劣化、轨道状态智能监测具有重要意义。模型是在存在明显速度变化区间的合理假设下成立的,但若列车在几十公里内均未发生速度变化的极端情况,可能会降低该模型的计算效率与准确性,未来可针对速度平稳区间的里程修正方法做进一步研究,对现存不足进行改进和补充,使模型更好地服务于轨检数据分析。