STAR-RIS辅助多载波通信感知一体化系统的资源优化
2024-03-27寇弘恺傅友华
寇弘恺, 傅友华,*
(1. 南京邮电大学电子与光学工程学院, 江苏 南京 210023; 2. 南京邮电大学柔性电子(未来技术)学院,江苏 南京 210023; 2. 南京邮电大学射频集成与微组装技术国家地方联合工程实验室, 江苏 南京 210023)
0 引 言
可重构智能表面(reconfigurable intelligent surface, RIS)因其在节能绿色通信方面的潜力,被视为在即将到来的第六代(sixth generation, 6G)无线通信网络中最大化数据速率和最小化功率的解决方案[1]。另一方面,商用无线通信服务的激增导致了频谱拥堵等问题,为了提升频谱利用率和降低硬件成本,6G希望将雷达系统和通信网络集成,形成一个通信感知一体化(integrated sensing and communications, ISAC)系统,也称为双功能雷达通信(dual-function radar-communications, DFRC)系统[2-4]。
RIS能够完全依靠无源可调谐元件控制其反射信号的相移,被视为智能无线电这一新兴概念的关键使能因素[5]。然而,传统的RIS只能将信号反射到表面的同一侧,这导致了发射机和接收机不在RIS同一侧时,通信系统不能享受RIS带来的优势。为了克服这一限制,目前已经出现了一种名为同时透射和反射的RIS(simultaneously transmitting and reflecting RIS, STAR-RIS)的新型智能表面[6],也叫做全向智能表面(intelligent omni-surfaces, IOS)[7]。它能够使入射到表面任一侧的无线信号被同时反射和透射。STAR-RIS为信号传播提供了增强的自由度,能够为表面的两侧用户提供服务,实现了全空间360°的覆盖[6]。文献[8-12]已经初步探索了在无线通信系统中部署STAR-RIS的优势。文献[8]制定了多载波通信网络的资源分配策略,联合优化信道和功率分配以及STAR-RIS的波束形成,比较了采用不同多址方案的系统和速率问题,提出了一种匹配算法来确定子信道分配,之后分别采用半正定规划(semidefinite program, SDP)、凸上界近似和几何规划优化解码顺序、波束形成系数向量和功率分配。文献[9]考虑了在STAR-RIS辅助的单播和多播通信系统中联合优化主动和被动波束形成以最小化发射功率的问题,并提出了3种STAR-RIS的实用操作协议,利用惩罚函数法和逐次凸逼近 (successive convex approximation, SCA)算法进行求解。
ISAC是一个完全共享的平台,能够传输双功能波形[13],从而提高频谱利用率和硬件效率[14]。对于ISAC来说,频分ISAC是一种常用的选择,通常基于正交频分复用(orthogonal frequency division multiplexing, OFDM)波形来实现[15-17]。具体来说,在给定信道条件、发射机功率预算等关键参数指标的情况下,通信和感知功能被分配给不同的子载波[2,18-19]。文献[2]研究了通信和雷达功能共存于同一带宽下的多载波波形,以提高频谱利用率,提出了两个联合设计范例,并分别用交替方向序列凸规划和分枝定界算法进行求解。文献[18]解决了在DFRC系统能够同时执行主要雷达目的和次要通信目的的一般情况下,设计联合子载波选择和功率分配方案以最小化DFRC系统功耗的问题,通过凸松弛重构和解耦,结合循环最小化算法和KKT(Karush-Kuhn-Tucker)最优性条件,提出了一种有效的联合优化方案三步求解技术。文献[19]研究了DFRC系统中的公平性问题,该系统利用OFDM波形同时执行雷达和通信操作,提出了一种新的迭代算法,在满足雷达性能约束的前提下,最大化不同通信用户之间的公平性。
本文首次将STAR-RIS与多载波ISAC系统相结合,利用它们各自的优势提高通信和感知性能。ISAC基站同时发送雷达和通信信号,在共用同一硬件资源的情况下实现通信和感知两种功能,在保证雷达功能的信噪比和STAR-RIS两侧用户各自的通信信噪比前提下,通过优化ISAC基站的功率和子载波分配以及STAR-RIS的波束成形系数,实现通信和速率最大化。这个问题是一个多变量耦合的非凸问题,难以直接求解。因此,本文将各个变量进行解耦,把原问题转化为3个凸的子问题,进行交替优化求解。具体做法如下:优化子载波分配时,将整数规划问题中的离散子载波选择变量进行松弛并利用惩罚函数法和SCA算法进行求解;涉及功率分配的子问题是一个直接凸问题,可以直接用凸优化的常用方法进行求解;优化STAR-RIS系数矩阵时,采用SDP算法和带惩罚项的SCA算法进行求解。
1 系统模型
如图1所示,考虑一个STAR-RIS辅助ISAC的系统, 单天线ISAC基站同时向目标和下行通信用户发射OFDM波形。
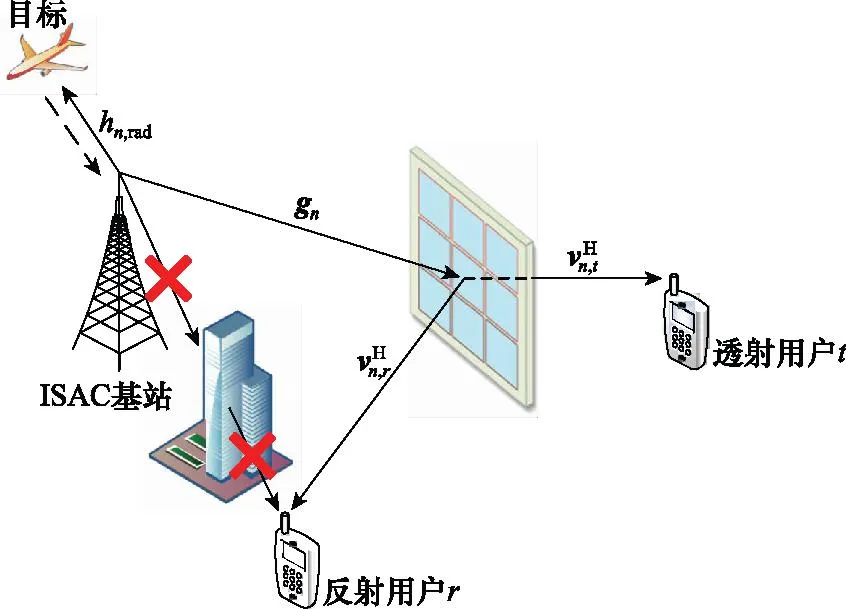
图1 STAR-RIS辅助ISAC系统Fig.1 STAR-RIS assisted ISAC system
两个单天线用户分别位于STAR-RIS的两侧,它们与基站之间的直接链路被阻挡。STAR-RIS部署在靠近用户的位置以有效地协助下行用户通信。同时,由于STAR-RIS部署在距离目标较远的地方,并且目标与ISAC基站有较强的直接链路,因此通过STAR-RIS反射的雷达回波信号较弱,可以忽略不计[14]。在实际应用中,雷达功能比通信功能所需要的功率往往更高,因此可以通过控制基站的发射功率以及基站和STAR-RIS之间的距离来实现上述假设。此外,本文假设所有的信道状态信息完全已知。
ISAC基站一共有N个相互正交的子载波,将位于基站同侧的用户命名为反射用户r,位于基站异侧的用户命名为透射用户t。因此,基站发送信号使用的双功能OFDM波形,可以建模[18,20]为
x=FIDFT[Frsr+Ftst+(I-Fr-Ft)srad]
(1)
式中:FIDFT表示离散傅里叶逆变换矩阵;向量sr=[s1,r,s2,r,…,sN,r]T∈CN×1和st=[s1,t,s2,t,…,sN,t]T∈CN×1是发送给用户r和t的频域通信信号;srad=[s1,rad,s2,rad,…,sN,rad]T∈CN×1是频域上的雷达发射信号;I∈CN×N是单位矩阵;Fr=diag(f1,r,f2,r,…,fN,r)和Ft=diag(f1,t,f2,t,…,fN,t)表示用户r和t的子载波选择矩阵,其元素的取值为{0,1}。对第n∈N{1,2,…,N}个子载波上用户k∈K{r,t}的子载波选择变量fn,k有以下定义:
(2)
其中,每个子载波只能分配给雷达功能或者一个用户,所以对∀n∈N有fn,r+fn,t≤1。因此,ISAC系统可以接收和处理雷达回波信号,下行链路通信用户可以解码通信信号,并且雷达和通信之间以及用户之间都是在互不干扰的情况下工作的。
1.1 通信模型
本文考虑STAR-RIS的能量分裂协议,所有的STAR-RIS元件既可以反射又可以透射,入射到每个元件上的信号能量被分裂为反射信号能量和透射信号能量。由M块元件组成的STAR-RIS的反射系数矩阵和透射系数矩阵分别为
(3)
(4)
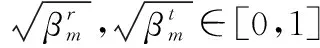
用户k∈K处的接收信号为
(5)
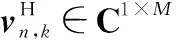
本文考虑ISAC基站到STAR-RIS及STAR-RIS到两个用户的信道为莱斯衰落信道[8]:
(6)
(7)
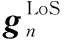
因此,用户k∈K在第n∈N个子载波上的信噪比为
(8)
由式(8)得到用户k∈K在第n∈N个子载波上的速率Rn,k为
(9)
1.2 雷达模型
ISAC基站处的雷达接收信号为
(10)
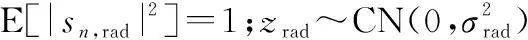
因此,雷达信噪比可表示为
(11)
本文假定hn,rad的幅值|hn,rad|为已知的,因为可以把目标当作在给定范围内可检测到的最小目标,这种假设在雷达设计中经常被采用[2]。
2 问题模型
为了提高整体数据速率,本文提出了一个联合子载波分配、功率分配、STAR-RIS反射和透射波束形成的优化问题,以最大化用户r和用户t可达到的总速率。优化问题如下:
(12)
C2:fn,r,fn,t∈{0,1},∀n∈N
C3:fn,r+fn,t≤1,∀n∈N
C9:0≤pn≤ξ,∀n∈N
式(12)的目标函数是两个用户的和速率,本文希望在满足约束的情况下最大化通信和速率;约束C1为每个用户的最低信噪比约束,以保证每个用户的通信质量,γcom表示最小的信噪比;约束C2表示子载波选择变量fn,r,fn,t的值只能取1或0;约束C3表示每个子载波最多分给一个用户,若没有分配给通信用户,则用于雷达感知功能;约束C4~约束C6是STAR-RIS的幅值和相位约束;约束C7是雷达信噪比约束,最小雷达信噪比为γrad;约束C8是系统的总功率约束,最大功率为Pmax;约束C9是每个子载波上的峰值功率约束,最大子载波峰值功率为ξ。为了防止系统将功率集中在一个或几个子载波上,在多载波系统中该约束是有必要的,否则将失去频率分集的优势,同时会降低距离分辨率[2]。
3 算法设计
由于式(12)是一个多变量相互耦合的非凸问题,使得问题难以直接求解,本文考虑使用交替优化,将子载波选择变量fn,k、子载波发射功率pn、STAR-RIS系数矩阵Θk依次进行优化,具体做法如下:首先,子载波选择变量fn,k是离散的,离散变量所涉及的优化问题往往复杂度很高且较难求解,所以本文在给定STAR-RIS的系数矩阵Θk和功率pn的情况下,利用连续化fn,k的惩罚函数法和SCA算法求解子载波分配的子问题;然后,固定STAR-RIS的系数矩阵Θk和子载波选择变量fn,k。优化功率分配变量pn时的子问题是凸的,可以直接求解;最后,根据获得的子载波选择变量fn,k和功率分配变量pn,利用SDP方法优化系数矩阵Θk并利用惩罚函数和SCA算法处理秩一约束。
3.1 优化子载波选择变量
固定Θk和pn优化fn,k时,有约束C1、约束C2、约束C3、约束C7,该子问题如下:
(13)
C2:fn,r,fn,t∈{0,1},∀n∈N
C3:fn,r+fn,t≤1,∀n∈N
约束C2中涉及到的变量是取值只能为0或1的离散变量,这使得该子问题成为较难求解的整数规划问题。为了便于求解,需要将该约束进行放松,因此本文施加新约束对变量fn,k进行放松:
0≤fn,k≤1
(14)
(15)
之后,fn,k被放松为连续变量,式(15)的等号当且仅当fn,k为0或1时取得。此时将式(15)作为惩罚函数,该子问题可以通过带有惩罚项的SCA算法进行求解,该子问题可被重写为
(16)
C2:0≤fn,k≤1,∀n∈N,∀k∈K
C3:fn,r+fn,t≤1,∀n∈N
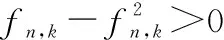
(17)

(18)
C2:0≤fn,k≤1,∀n∈N; ∀k∈K
C3:fn,r+fn,t≤1,∀n∈N
至此,该子问题被转化为一个凸问题,可以通过标准的凸优化求解器(matlab software for disciplined convex programming, CVX)[21]有效地解决。
3.2 优化功率分配变量
固定Θk和fn,k优化pn时,有约束C1、约束C7、约束C8、约束C9,该子问题如下:
(19)
C9:0≤pn≤ξ,∀n∈N
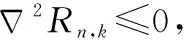
3.3 优化STAR-RIS系数矩阵
固定fn,k、pn,优化Θk时,有约束C1、约束C4、约束C5、约束C6,该子问题如下:
(20)
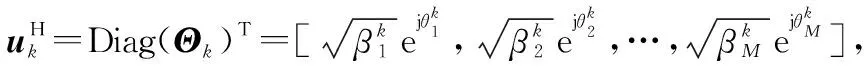
(21)
0≤[Uk]m,m≤1,∀m∈M;∀k∈K
[Ut]m,m+[Ur]m,m=1,∀m∈M
Uk≥0,∀k∈K
rank(Uk)=1,∀k∈K
由于秩一约束是非凸的,此前大多数的此类工作往往是忽略该约束进行求解,而得到的解Uk往往不能满足秩一约束,之后采用高斯随机化得到uk,而此方法得到的解具有不确定性。本文将秩一约束写为如下形式[9]:
(22)
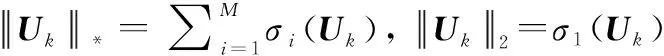
(23)
0≤[Uk]m,m≤1,∀m∈M; ∀k∈K
[Ut]m,m+[Ur]m,m=1,∀m∈M
Uk≥0,∀k∈K
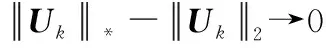
(24)
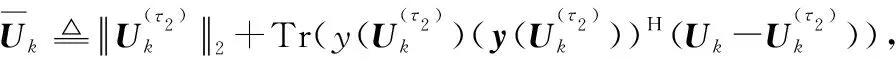
(25)
0≤[Uk]m,m≤1,∀m∈M,∀k∈K
[Ut]m,m+[Ur]m,m=1,∀m∈M
Uk≥0,∀k∈K
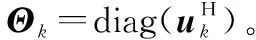
3.4 复杂度分析

算法1总结了本文提出的交替优化方案。

算法1 交替迭代算法输入 初始化可行解Θ(0)k,p(0)n,f(0)n,k,惩罚因子η1,η2,惩罚因子更新系数ω1,ω2,其中ω1>1,ω2>1输出 子载波选择变量fn,k,功率分配变量pn,STAR-RIS系数矩阵Θkrepeat 令迭代次数τ=0 repeat 令迭代次数τ1=0,f(τ1)n,k=f(τ)n,k repeat 对于给定的Θ(τ)k,p(τ)n,f(τ1)n,k求解式(18),用获得的解更新f(τ1+1)n,k 令τ1=τ1+1 until:收敛或者达到最大迭代次数 令f(τ+1)n,k=f(τ1)n,k,对于给定的Θ(τ)k,以f(τ+1)n,k求解式(19),用得到的值更新p(τ+1)n 令迭代次数τ2=0,Θ(τ2)k=Θ(τ)k repeat 对于给定的Θ(τ2)k,p(τ+1)n,f(τ+1)n,k求解式(25),用获得的解更新Θ(τ2+1)k 令τ2=τ2+1 until:收敛或者达到最大迭代次数 令Θ(τ+1)k=Θ(τ2)k,τ=τ+1 until:收敛或者达到最大迭代次数 更新惩罚因子η1=ω1η1,η2=ω2η2,Θ(0)k=Θ(τ)k,p(0)n=p(τ)n,f(0)n,k=f(τ)n,kuntil:惩罚项低于阈值或者达到最大迭代次数
4 仿真分析

图2展示了本文所提方案的收敛情况,其中系统总发射功率Pmax=36 dBm,γrad=5 dB,M=10。图2中,圆形实线代表本文目标函数通信和速率,星形实线代表所有惩罚函数里面最大的一项。可以看到在第4次迭代之后,通信和速率基本保持不变,而此时式(18)和式(25)中惩罚函数的最大值也随着迭代减小到一个理想的范围内,并且在此之后也基本保持不变,由此可以看出本文所提方案的快速收敛性和有效性。
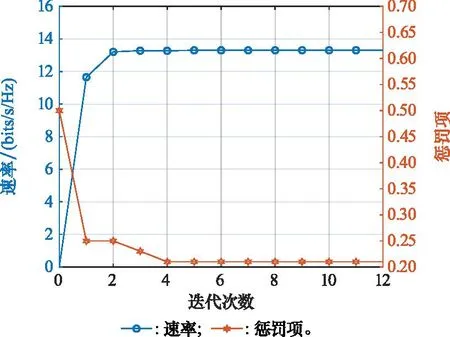
图2 本文所提算法迭代收敛行为Fig.2 Iteration and convergence behavior of the proposed algorithm
图3展示了子载波和功率的分配情况。从图中可以看出,反射用户获得了较多的子载波资源,这是受用户信道条件影响的原因。当某个用户的信道条件较好时,大量的资源会优先分给该用户,以最大程度地提高通信和速率。虽然透射用户分到的子载波较少,但是依然能够满足通信用户的最低信噪比约束,从而保证了每一个用户的通信质量,杜绝了某个用户因为所处位置信道条件较差而被忽视的情况。本文所提方案在透射用户和反射用户为多个用户时依然有效。同样,雷达功能获得的子载波也相对较少,却也满足雷达信噪比约束,从而保证了ISAC的感知功能。从图3中还可以发现一个情况:有的子载波(例如:索引为60的子载波)没有分配给任何一种功能。这说明了某个子载波在通信或感知时信道条件都不如别的子载波,此时该子载波将会被抛弃,系统将会把更多的功率资源投向别的子载波。
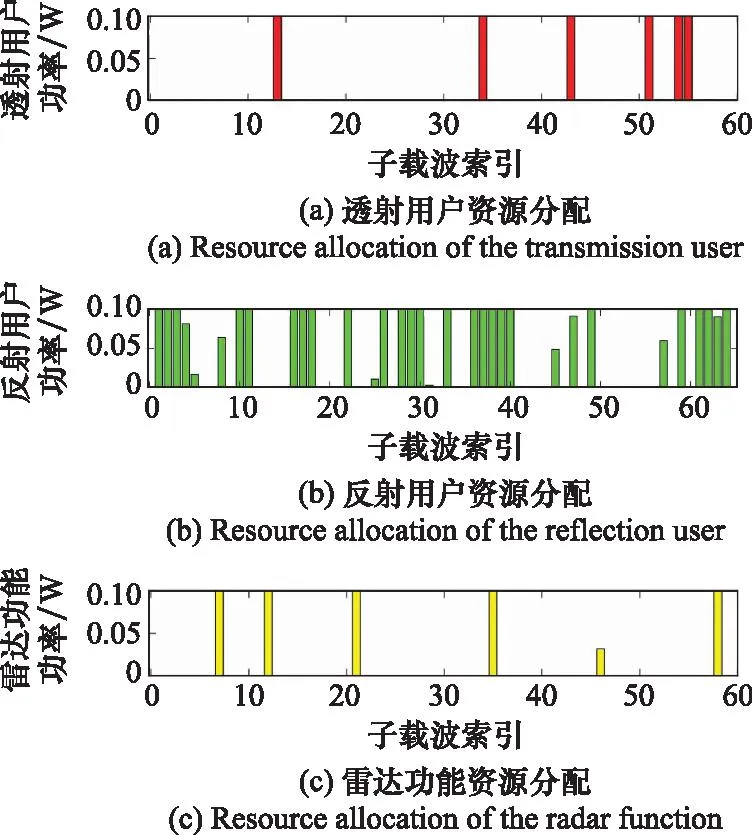
图3 资源分配最优结果Fig.3 Optimization results for resource allocation
图4描绘了每个STAR-RIS元件的反射信号和透射信号的振幅值。所有STAR-RIS元件透射振幅和反射振幅的平方之和为1,满足约束条件C4的能量守恒定理。从图4中还可以发现,大部分STAR-RIS元件的反射系数幅值相对较大,这也印证了图3的分析。信道条件较好的用户分得较多的子载波和功率资源以提高和速率,而在这一过程中STAR-RIS通过调整振幅,使这一优势进一步扩大。另一方面,这种设计还保证了信道条件差的用户的最低通信需求,否则在极端情况下,可能出现所有STAR-RIS元件的透射幅值全为1、反射幅值全为0,或者透射幅值全为0、反射幅值全为1的现象。因此,图4大大体现了约束C1存在的意义以及STAR-RIS可以实现360°通信的优势。
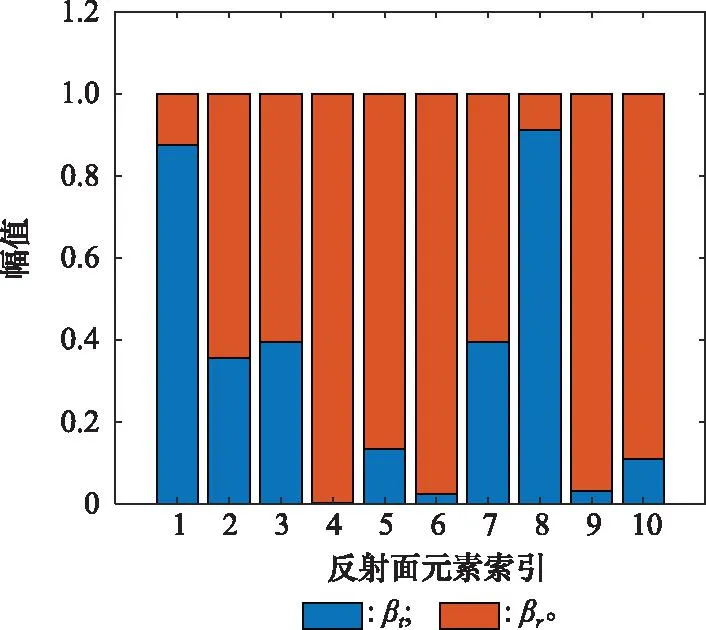
图4 STAR-RIS元件透射和反射信号幅值的调整Fig.4 Adjustment for the values of the transmission and reflection signals’amplitudes for each STAR-RIS element
图5给出了通信和速率与STAR-RIS元件个数的关系。为了验证本文所提方案的有效性,将所提方案与另外3种方案进行比较。从图5中可以看出,各种方案的通信和速率都会随着STAR-RIS元件个数的增加而增加,这是由于更多的STAR-RIS元件将带来更高的自由度,更多的散射单元在用户处带来更高的波束形成增益和空间自由度,改善了通信信道质量,功率资源会更倾向于分配到信道条件好的通信链路[8.31]。不具备雷达功能指的是基站不具备感知功能,而单纯地服务下行用户,这种方案比本文所提方案有着更高的通信速率,这是因为原本用于雷达感知功能的子载波和功率资源也分配给了通信功能,速率自然也会随之增加。为了公平地比较,传统RIS指的是将一个配有M/2个元件、只能反射的RIS和一个配有M/2个元件、只能透射的RIS部署在相邻的位置,其中M为偶数[9]。STAR-RIS可以根据信道条件动态地调整两个面的幅值,而传统RIS只能保持振幅为1,即使某个子载波上的信道条件较差,也不能做出改变,因此STAR-RIS相比于传统RIS的性能得到大幅度提高。对于随机相移方案,由于其透射幅值、反射幅值、透射相移、反射相移都是随机的,所以其性能最差。
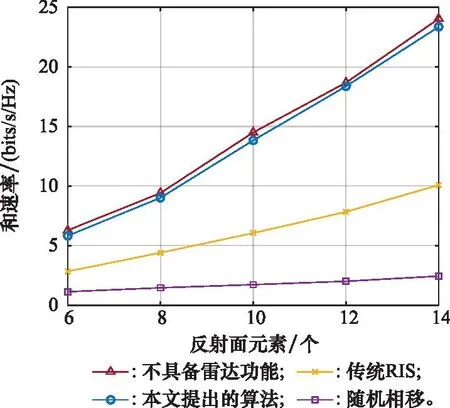
图5 STAR-RIS元件数量与通信和速率的关系Fig.5 Relationship between the number of STAR-RIS elements and the sum-rate of communication
图6展示了系统总功率与通信和速率之间的关系。当系统总功率不断增加时,各种方案的速率都随之增加,这也符合常理。各种方案之间的差距类似于图5的分析,这里不再赘述。
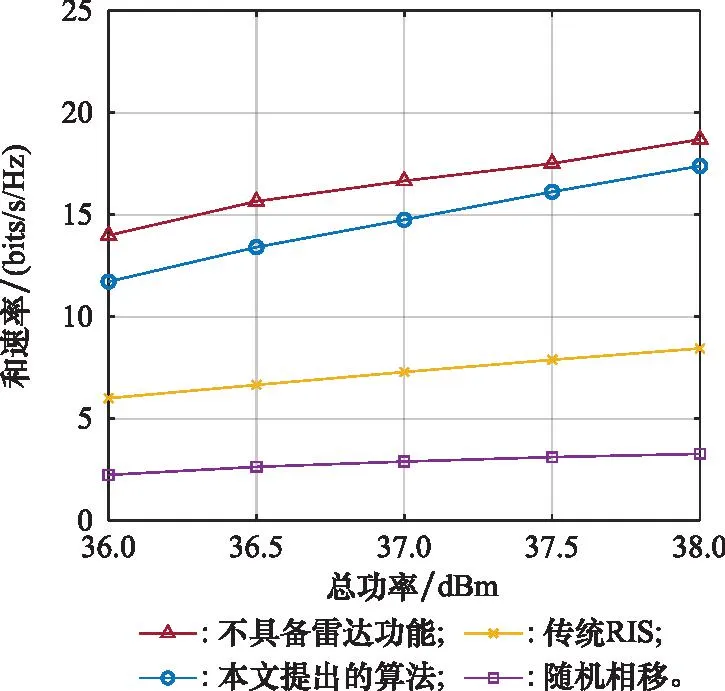
图6 系统总功率与通信和速率的关系Fig.6 Relationship between the total transmit power and the sum-rate of communication
图7展示了雷达的最低信噪比与通信和速率之间的关系。从图7可以看到,不具备雷达功能的方案得到的通信和速率始终保持不变,这是因为该方案相当于没有雷达信噪比约束,所以和速率不会随横坐标而改变。理论上,最低雷达信噪比设置越高,通信功能获得的资源就会越小,速率自然会下降。随机相移方案虽然下降不够明显,但是这3种方案的总体趋势还是随着最低雷达信噪比约束的增加而降低。
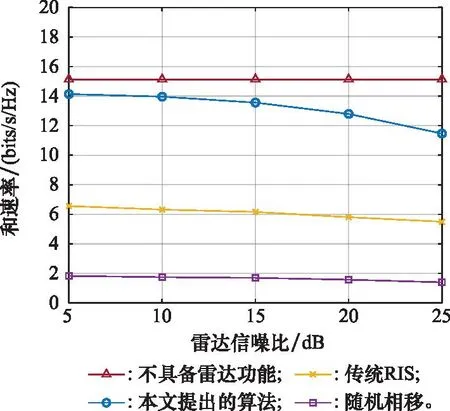
图7 雷达最低信噪比与通信和速率的关系Fig.7 Relationship between the radar signal to noise ratio constraint and the sum-rate of communication
5 结 论
本文将STAR-RIS和ISAC这两项有前景的新兴技术进行了结合,不仅实现了360°全向通信,还通过共享相同硬件资源实现了通信和感知两种功能。通过优化设计ISAC基站端的功率和子载波资源分配以及STAR-RIS的系数矩阵,以最大化通信和速率。利用交替优化算法,将原问题解耦转化成3个凸的子问题并分别进行求解。仿真实验结果表明,在性能损失很小的情况下,在通信的基础上增加了感知功能,验证了本文所提方案的有效性。后续将考虑一些复杂度更低的高效算法,以及STAR-RIS服务雷达功能的场景。
