可旋转翼式弹道修正组件滚转控制技术研究

2024-03-27郑秋实许伟春赵明翰李乃星包旭馨

系统工程与电子技术 2024年4期

郑秋实, 许伟春, 赵明翰, 李乃星, 包旭馨

(1. 上海无线电设备研究所, 上海 201109; 2. 上海航天技术研究院, 上海 201109)

0 引言

为满足现代战争对低成本、高精度制导弹药的需求,简易制导弹药技术应运而生。其中,弹道修正组件技术凭借其成本低、结构简单、精度高等优点,受到越来越多的青睐,具有广阔的发展前景[1-3]。弹道修正组件上安装有制导控制模块和执行机构,可以采用同等封装直接替换炮弹引信,将常规无控炮弹改进为具备制导控制能力的弹道修正弹。在飞行过程中,修正组件可以实时获取弹道信息,发出指令,控制执行机构对飞行弹道进行修正,从而减小弹着点偏差,提高命中精度[4-6]。弹道修正组件的执行机构通常采用鸭舵机构,根据舵片能否旋转,弹道修正组件可分为固定翼式和可旋转翼式[7]。

固定翼式修正组件的结构较为简单,其鸭舵偏转角是固定不变的,无法改变控制力大小和方向,因此很难在飞行弹道内进行全程修正。此类固定翼式修正组件通常采用电磁执行机构控制组件的滚转运动。程杰等[8]研究了不同发射条件下修正组件电磁执行机构的工况,为后续电磁执行机构的设计提供了初期设计指标,随后通过瞬态数值计算和动态风洞试验研究了双旋弹内回路的滚转特性,并通过飞行试验进行验证[9]。殷婷婷等[10]基于电磁执行机构力矩输出特性测试试验,研究建立了修正组件控制响应模型,随后基于得出的模型,提出了一种基于扩张状态观测器(extended state observer, ESO)的转速控制器[11],通过设计输出反馈型ESO对系统整体扰动进行估计,并以前馈的方式进行补偿,以减弱模型不确定性和扰动对跟踪性能的影响。张鑫等[12]通过对电磁执行机构电气原理的分析,建立了更为准确的修正组件滚转通道动力学模型,并设计了两自由度H∞回路整形滚转通道控制器,实现了精确的滚转角控制。

相比于固定翼式,可旋转翼式修正组件的鸭舵偏转角是连续可控的,可以借鉴常规旋转弹的控制方式,对弹药的飞行弹道进行制导控制,因此能够获得更高的精度。Ilg[13]提出的智能弹药控制方案采用了比例式舵机控制的一对鸭舵进行单通道正弦控制,以实现二维弹道修正。朱大林[14]在其博士论文中采用了两对可旋转鸭舵进行双通道旋转控制,实现了双旋弹道修正弹的二维弹道修正,并对其飞行稳定性进行了分析[15]。但是两者并没有对修正组件滚转通道进行控制,而是通过自然减旋运动使组件转速保持在低速旋转状态。为获取更高的控制精度,Theodoulis等[16]基于H∞控制理论研究设计了双旋弹倾斜转弯(bank-to-turn, BTT)自驾仪,并指出对修正组件滚转角的快速精确控制是极其关键的。针对修正组件滚转控制问题,Salman 等[17]采用了经典比例-积分-微分(proportion-integral-derivative, PID)控制方法和H∞控制理论设计了滚转通道控制器,Theodoulis等[18]采用固定结构H1控制方法设计了155 mm鸭舵控制双旋弹的前体滚转通道自驾仪,实现了对双旋弹前体滚转角的快速精确控制。

综合前人研究发现,使用可旋转翼式弹道修正组件的弹道修正弹,可以采用常规旋转弹使用的BTT控制方式,以获取更高的制导控制精度,而修正组件滚转角的快速精确控制是实现BTT控制的关键。然而,在实际的弹道修正组件系统中,受限于安装空间和低成本要求,无法安装过多的传感器,许多系统状态变量无法通过直接测量获取,因此一些复杂度较高的控制方法并不适用。同时,由于弹道修正弹飞行跨域大,系统具有强非线性,并且存在气动参数摄动、摩擦等未建模干扰力矩以及外部干扰等问题,这些问题大大增加了修正组件滚转控制的难度。目前针对可旋转翼式修正组件滚转控制的研究较少,已有的几篇文献(文献[16-18])均基于线性化鲁棒控制理论,缺乏稳定性保证,并且设计难度大、耗时长,难以在实际工程中实现。

针对此类非线性不确定系统的一种有效方法是滑模控制法[19-24],其具有响应速度快、对扰动和参数变化不敏感等优点,但是同时具有抖振问题、结构复杂等缺点,并且滑模控制需要的已知系统状态量较多,因此普通滑模控制法并不适用于弹道修正组件。韩京清等[25-26]针对一类存在不确定性的系统,提出一种ESO对系统的不确定性进行估计。ESO可以估计系统的状态以及不确定性和干扰的影响,从而实现干扰抑制或补偿。文献[27-29]均利用ESO对系统中的扰动和变量进行估计,从而达到良好的控制精度和抗干扰能力。Wang等[30]对ESO、高增益观测器(high gain observer, HGO)和滑模观测器(sliding mode observer, SMO)这三种观测器进行了比较研究,结果表明ESO在处理不确定性、干扰和传感器噪声方面总体性能更优。

基于以上研究,本文提出一种基于ESO的滑模控制方法,首先针对可旋转翼式弹道修正组件的特点,介绍了修正组件的控制原理,接着通过对修正组件所受力矩进行分析,建立了修正组件滚转通道的动力学模型;然后将系统存在的气动参数不确定性、未建模摩擦干扰和外部干扰整合为一个总的复合干扰,设计ESO对该复合干扰以及实际工程中无法直接测量的状态变量进行估计,随后结合滑模控制理论,设计具有足够鲁棒性的滚转通道控制器,并进行了稳定性分析;最后利用Simulink仿真实验进行验证,并对仿真结果进行分析及得出结论。本文设计的修正组件滚转控制器只需要一个滚转角反馈信号,既能够对速度、加速度和复合干扰信号进行观测,同时又能够对系统中未建模摩擦力、随机外部干扰和参数不确定性造成的复合扰动进行抑制,保证滚转控制器具有较高的滚转角跟踪精度和鲁棒性。

1 可旋转翼式修正组件滚转控制原理

可旋转翼式修正组件通常采用电动舵机作为执行机构,控制两对鸭舵按照指令连续偏转。如图1所示,修正组件上安装有两对鸭舵,其中舵片1和舵片3构成一对差动舵,可为修正组件提供导转力矩,舵片2和舵片4构成一对同向舵,用于产生侧向控制力和控制力矩。修正组件与弹体之间通过轴承连接,两者之间可以相对自由旋转。当需要产生某方向控制作用时,滚转通道控制器通过控制差动舵偏转,控制修正组件旋转至预定角度,然后同向舵偏转,产生一定方向和大小的控制力,进而控制弹体飞行方向。

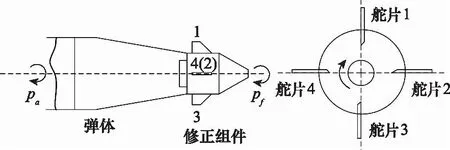
图1 可旋转翼式弹道修正组件示意图Fig.1 Schematic diagram of the trajectory correction fuse with active-canards

2 修正组件滚转通道建模

2.1 修正组件滚转力矩分析

首先对弹道修正组件在飞行过程中所受滚转力矩进行分析,如图2所示,修正组件受到的滚转力矩包括:差动舵1～差动舵3产生的控制力矩TC,由组件滚转引起的气动阻尼力矩Tpf,组件与弹体之间的滚转阻尼力矩Tf。图中pf为组件滚转速度,pa为弹体滚转速度,φf为组件滚转角度。设定组件与弹体旋转方向相同(从弹头看向弹尾,逆时针旋转),并设定此方向为滚转速度和滚转力矩的正方向。

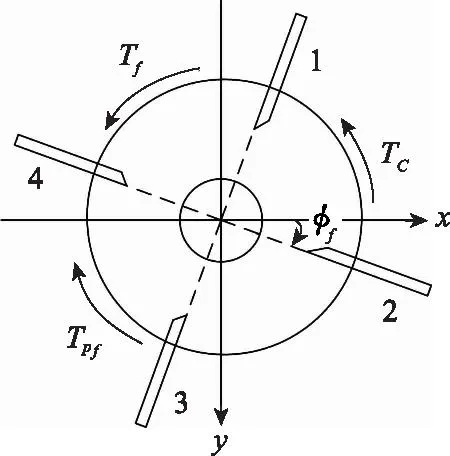
图2 修正组件所受力矩分析Fig.2 Moments analysis of the correction fuse

差动舵控制力矩的表达式为

(1)

气动阻尼力矩表达式为

(2)

式中:ρ为大气密度;S为参考面积;L为参考长度;V为弹丸飞行速度;δx为差动舵偏角;CMδx和Clpf分别为差动舵控制力矩系数导数和组件气动滚转阻尼力矩系数导数,可通过计算流体动力学(computational fluid dynamics, CFD)气动仿真或者风洞试验获得。

组件与弹体之间的滚转阻尼力矩由轴承的粘性阻尼力矩和滚转摩擦力矩组成,粘性阻尼力矩与组件和弹体相对转速有关,滚转摩擦力与轴承所承受的法向力有关,具体表达式为

Tf=CV(pa-pf)+CR|FN|sgn(pa-pf)

(3)

式中:CV为粘性阻尼力矩系数;CR为滚转摩擦力矩系数;FN为作用在轴承上的法向力;sgn(·)为符号函数。其中,粘性阻尼力矩系数和滚转摩擦力矩系数的理论值较为复杂,一般可通过实验方法进行估计。

综上所述,修正组件滚转通道所受的总滚转力矩为

Tx=TC-Tpf+Tf

(4)

完成对组件所受力矩的分析后,即可开始进行滚转通道建模。

2.2 修正组件滚转通道建模

修正组件滚转通道模型包括如下的姿态角运动学方程和转速动力学方程:

(5)

式中:Ixf为修正组件的轴向转动惯量。将各力矩表达式代入式(5),可得:

(6)

式中:滚转阻尼力矩Tf的理论值及计算值较为复杂,并且在实际工况中,还会存在弹道初始扰动、随机风等各种扰动的影响。为简化分析,本文将滚转阻尼力矩和各种其他干扰力矩统一视为外部干扰dext进行处理。同时,考虑将差动舵动力学模型视为如下一阶环节:

(7)

式中:δx(s)为差动舵输出;δxc(s)为差动舵指令;Ts为差动舵系统时间常数。由式(6)和式(7)可得修正组件滚转通道模型框图如图3所示。

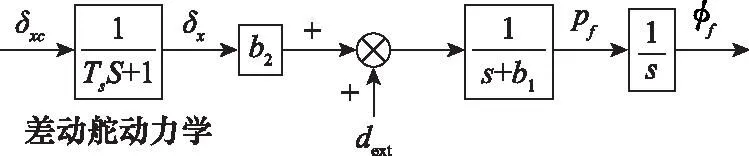
图3 滚转通道模型框图Fig.3 Block diagram of the roll channel model

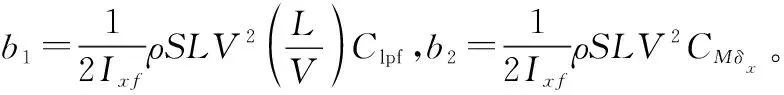
(8)

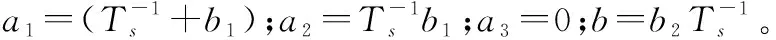
由此得到的是理想被控对象的传函,而在实际系统中还存在参数不确定性和外部干扰的影响。本文将参数不确定性体现为式(8)中参数ai(i=1,2,3)和b的摄动,定义参数ai=ai0+Δai和b=b0+Δb。其中,ai0和b0代表各参数的标称值,Δai和Δb代表各参数的摄动值。

当考虑参数不确定性和外部干扰时,将式(8)代表的被控对象改写为如下的空间状态方程:

(9)

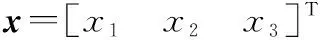
(10)

deq代表施加于系统的复合干扰,包含了未建模摩擦干扰、外部干扰和参数不确定性,其表达式为

d-Δa3x1-Δa2x2-Δa1x3+Δbu+ω

(11)

式中:ω为外部干扰。由此,得到考虑参数不确定性和外部干扰影响的滚转通道控制模型。下面将针对此模型设计能够理想地跟踪输入信号并且对参数不确定性和外部干扰具有足够鲁棒性的滚转控制器。

3 基于ESO的滑模控制器设计

本节将ESO与滑模控制理论相结合,针对修正组件滚转通道设计出滚转角控制器。控制系统框图如图4所示。

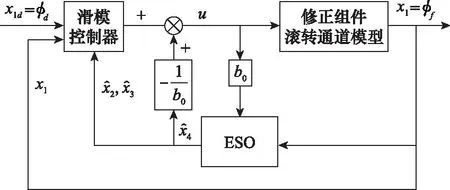
图4 修正组件滚转通道控制系统框图Fig.4 Block diagram of roll channel control system for correction fuse

首先,设计ESO对系统中无法直接测量的状态变量和由未建模摩擦干扰、外部干扰和参数不确定性等引起的复合干扰量d进行估计;然后利用滑模控制理论,设计滚转角控制器,并对控制量进行复合干扰补偿;最后通过Lyaponov稳定性理论验证闭环控制系统的稳定性。

3.1 ESO设计

不同于传统的观测器,ESO将作用在系统中的不确定性和扰动估计为原始系统的扩张状态,由此被称为ESO。ESO是相对独立于系统的数学模型,结构内部固有鲁棒性,性能更好并且易于实现。

考虑式(9)表示的系统模型,将复合干扰d设计为系统的一个扩张状态x4,则式(9)中的系统可改写为如下的状态空间形式:

(12)

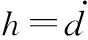
(13)

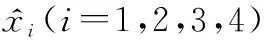
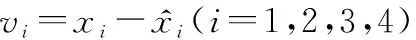
(14)

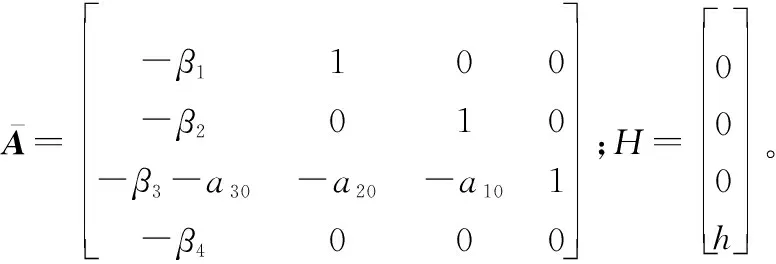
3.2 基于ESO的滑模控制器设计

本节将利用第3.1节中ESO对系统状态和总干扰的估计值,结合滑模控制理论进行控制器设计。

针对式(9)表示的修正组件滚转通道系统模型,定义滚转角跟踪误差为

e=x1-x1d

(15)

式中:x1d为滚转角指令,设计滑模函数为

(16)

式中:c1和c2为常数,且满足Hurwitz稳定条件,对式(16)求导可得:

(17)

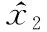
(18)

(19)

4 闭环控制系统稳定性

首先定义滑模控制器的Lyapunov函数为

(20)

对Vs求导可得:

(21)

将式(19)代入式(21)并化简后可得:

(22)

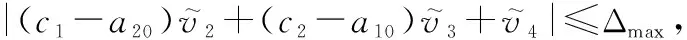
(23)

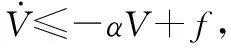
(24)

式中:α为任意常数。

(25)

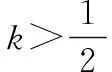
(26)

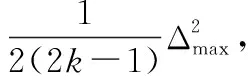
然后定义ESO的Lyaponov函数为

Vo=vTPv

(27)

对式(27)求导可得:

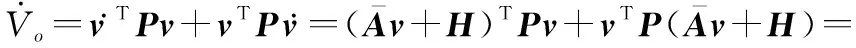
(28)

式中:λmin(Q)为Q的最小特征值,由式(28)可知ESO的收敛条件为

(29)

综合考虑ESO和滑模控制器构成的闭环系统,定义Lyapunov函数为

(30)

对式(30)求导,则有:

(31)

5 仿真结果与分析

在实际飞行过程中,弹道修正弹在不同时刻的飞行速度、转速、所受气动力等均不同,而修正组件的转速和受力也不同。因此,为验证本文所设计的滚转通道控制器的有效性,对所建立的滚转控制系统进行仿真分析,从而得出最终结论。

假设 1弹道修正弹初始发射速度为V=500 m/s,出炮口后弹体转速为1 445 rad/s,修正组件转速接近30 rad/s。图5为弹丸在全弹道内的飞行速度曲线,从图中可以看出,弹丸发射后,飞行速度先减小,30 s左右弹丸飞至弹道顶点,随后速度开始增大。

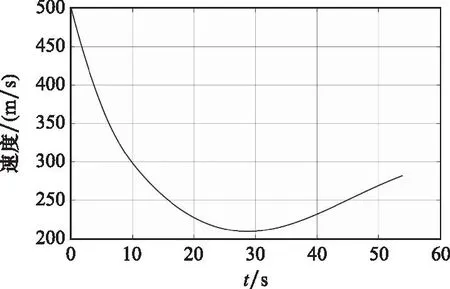
图5 飞行速度曲线Fig.5 Flight speed curce

图6为出炮口后弹体和修正组件的转速曲线,从图中可以看出,弹丸发射后,弹体转速随时间衰减,但是仍然维持高速旋转;修正组件在炮管内运动时受到摩擦力作用而转速增大,在出炮口后同时受到气动阻力力矩影响,在全弹道内维持约30 rad/s左右的低速旋转运动。

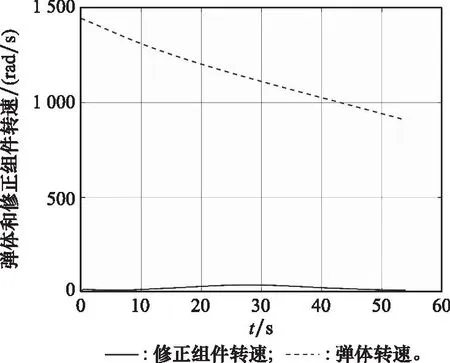
图6 修正组件转速曲线Fig.6 Spin rate curve of the correction fuse

修正组件主要物理参数如表1所示。

表1 物理参数Table 1 Physical parameters

修正组件主要气动参数包括组件气动滚转阻尼力矩系数导数Clpf和差动舵控制力矩系数导数CMδx。在飞行过程中,这两个系数不是固定不变的,而是与弹丸的飞行马赫数有关,表2给出了这两个气动参数随飞行马赫数的变化情况,图7给出了在参考弹道中这两个气动参数随时间的变化曲线。

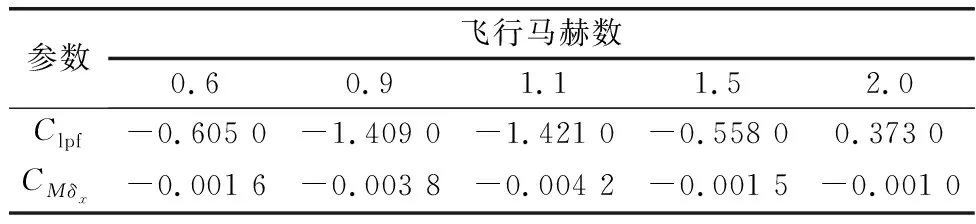
表2 气动参数Table 2 Aerodynamic parameters

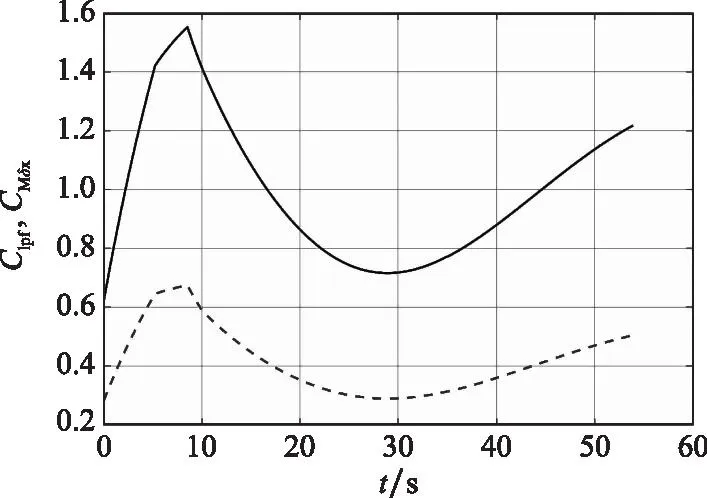
图7 气动参数曲线Fig.7 Aerodynamic parameter curves

5.1 基于ESO的滑模控制器性能仿真

弹道修正弹在弹道前半段,其外部环境和弹体本身运动状态变化较为剧烈,因此一般采取弹道顶点作为制导控制的起控点。本文取飞行时间30 s作为仿真起始点,仿真起始时刻弹体速度为210 m/s,修正组件滚转角为50°,转速为37 rad/s。

起控后,修正组件滚转角首先回到零位,然后开始跟踪幅值为±40°的阶跃指令。在仿真开始后第18 s,假设修正组件受到外部干扰力矩作用,产生的转动加速度干扰量为dext=300 rad/s2,将其按照下式转换到输入端,即可得到式(11)中的等效复合扰动值:

(32)

为保证ESO估计信号的快速性和对噪声的低敏感性,ESO的带宽折中取为ωE=80 Hz,则经计算可得ESO的增益:

(33)

综合考虑控制系统稳态和动态性能,保证滚转控制系统调节时间小于0.5 s,超调量小于5%,稳态误差小于0.1°,滑模控制器参数经调试后配置为c1=90,c2=17,k=200。仿真结果如图8～图12所示。

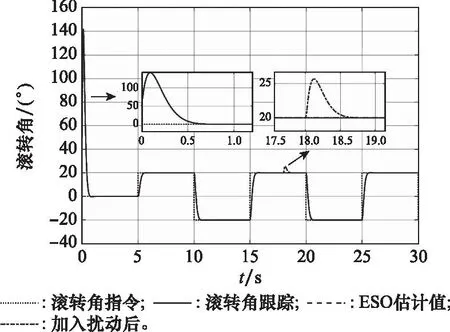
图8 滚转角指令、跟踪和观测值曲线Fig.8 Curves of roll angle command, tracking, and observed value

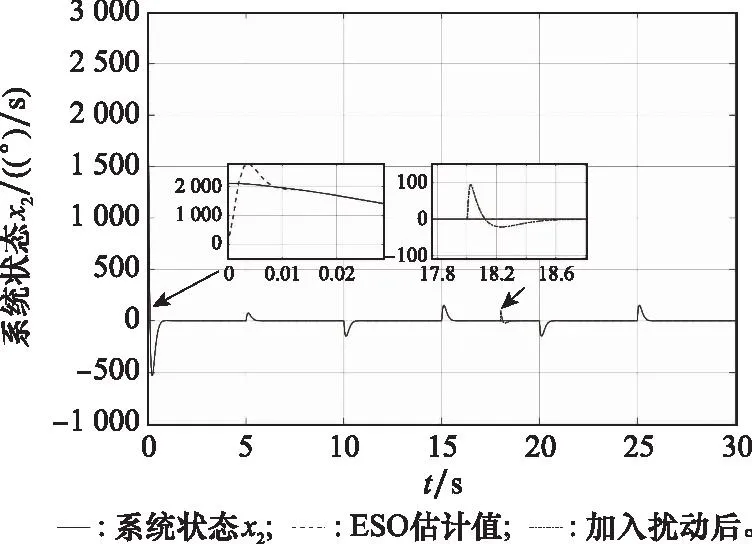
图9 系统状态x2曲线Fig.9 System state curves of x2

由图8中的滚转角跟踪曲线可以看出,本文提出的ESO滑模控制器能够快速稳定地控制修正组件达到预定的滚转角预定值。从图12中的控制量曲线可以看出,在加入外部扰动后,控制器输出量能够在很短时间内补偿跟踪误差,说明本文设计的控制器对外部干扰具有很好的抑制作用。从图8～图10中ESO对系统状态的估计值曲线可以看出,本文设计的ESO能够在很短时间内跟踪上实际信号。从图11可以看出,在外部干扰出现瞬间,ESO能够及时对其进行估计,说明本文设计的ESO满足系统要求,能够有效地对系统状态变量和外部干扰量进行准确估计。

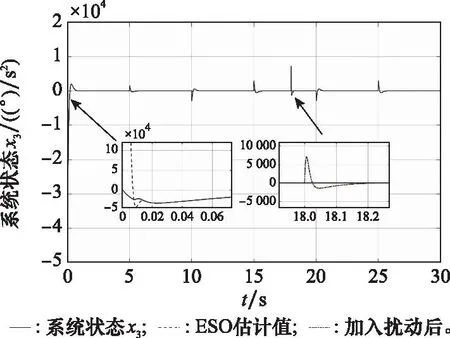
图10 系统状态x3曲线Fig.10 System state curves of x3

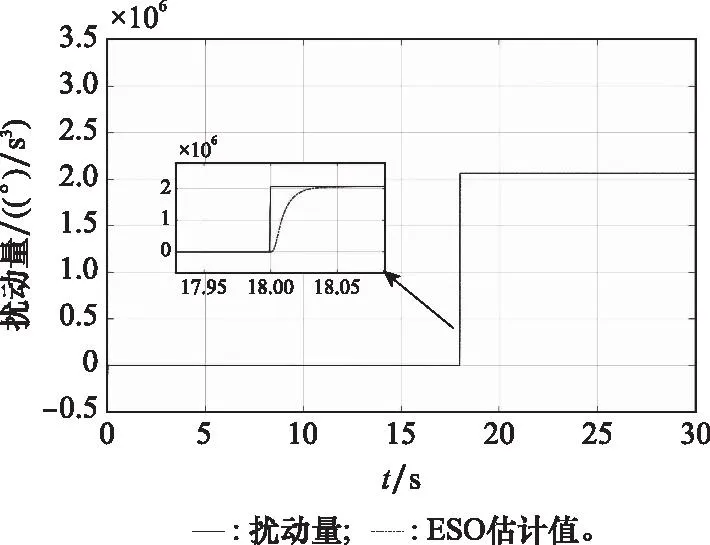
图11 干扰量及其观测值曲线Fig.11 Curves of disturbance and its observed value

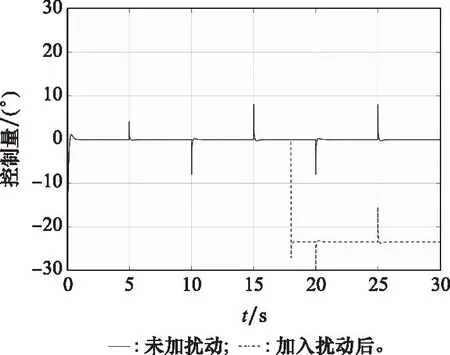
图12 控制量曲线Fig.12 Curve of control quantity

除了外部扰动,在实际飞行过程中,由于建模误差、计算误差等因素,式(9)中的参数a1,2,3和b的真实值会在其标称值a10,20,30和b0附近摄动,此时上述参数可表示为a1,2,3=a10,20,30+Δa1,2,3和b=b0+Δb,Δ代表了摄动量。为验证当存在系统参数不确定性时本文设计的控制器的性能,假设系统中参数的摄动量为±40%并进行仿真。仿真结果如图13和图14所示。

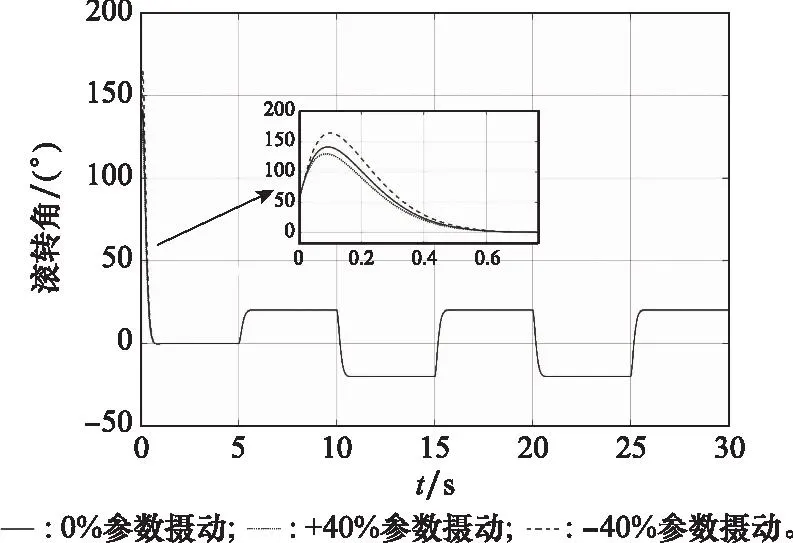
图13 参数摄动下滚转角跟踪曲线Fig.13 Roll angle tracking curves with parameter perturbations

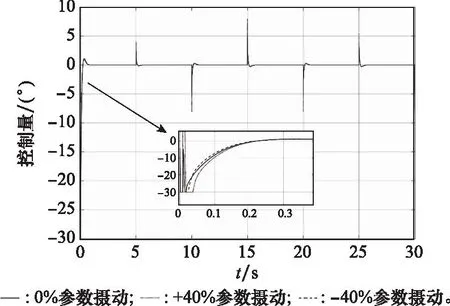
图14 参数摄动下控制量曲线Fig.14 Control deflection curves with parameter perturbations

从图中可以看出,本文设计的滚转控制器在存在参数摄动情况下,仍有较好的稳态性能,说明系统具有较强的鲁棒性。

5.2 连续性扰动下控制器性能仿真

第5.2节仿真验证了突发性外部扰动条件下控制器的性能。而弹丸在实际飞行过程中,还会受到随机风等连续性扰动的影响。基于第5.1节仿真条件,全程加入随机风等连续扰动,假设该连续扰动为正弦形式:dext=20·sin(2πt),仿真结果如图15～图19所示。

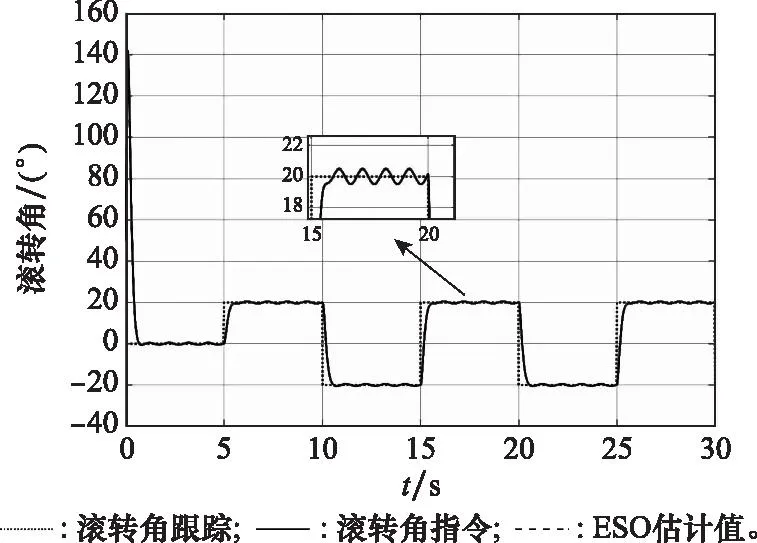
图15 滚转角指令、跟踪和观测值曲线Fig.15 Curves of roll angle command, tracking and observed value

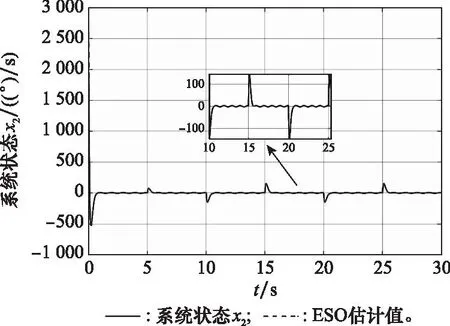
图16 系统状态x2曲线Fig.16 System state curves of x2

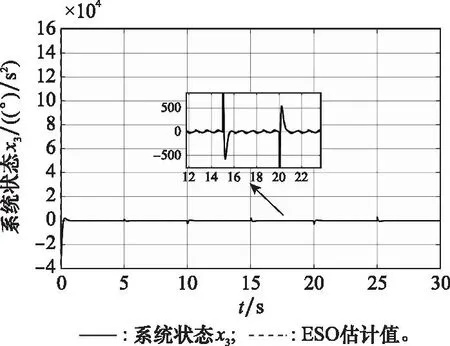
图17 系统状态x3曲线Fig.17 System state curves of x3

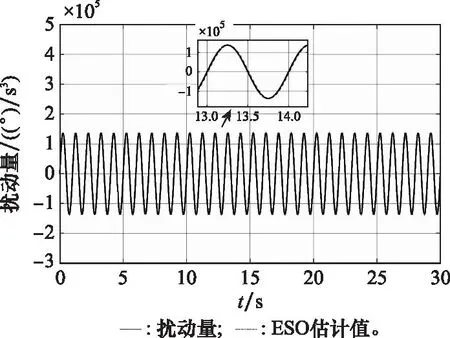
图18 干扰量及其观测值曲线Fig.18 Curves of disturbance and its observed value

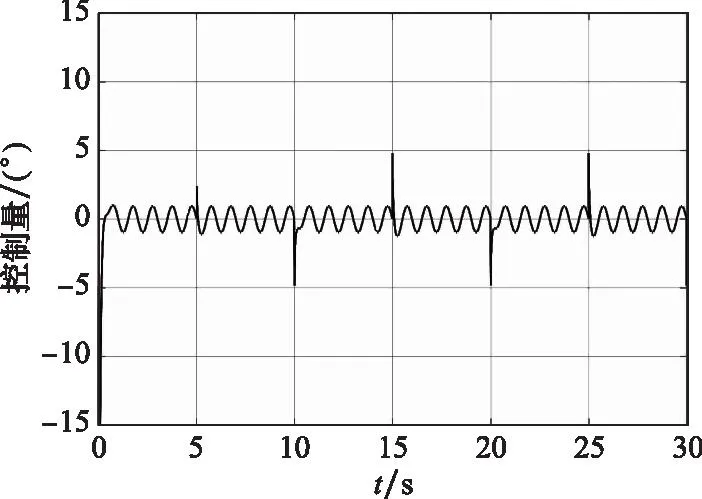
图19 控制量曲线Fig.19 Control quantity curve

从图15～图19可以看出,本文设计的滚转控制器在存在随机风等连续性外部扰动时,仍具有较好的控制性能。

5.3 与其他控制器性能对比

为验证本文设计的ESO滑模控制器的性能,对系统模型分别采用普通滑模控制和传统PID控制,并将控制结果与本文控制器做对比研究,仿真结果如图20所示。

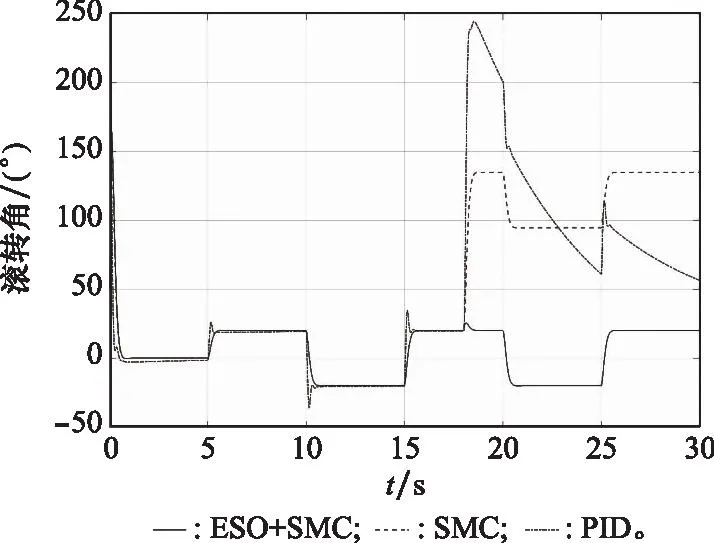
图20 不同控制器性能对比Fig.20 Performance comparison for different controllers

从图15中的滚转角跟踪曲线可以看出,普通滑模控制器的跟踪误差和超调量小,调节时间短,而传统PID控制器的跟踪误差和超调量较大。在外部强扰动作用下,普通滑模控制器和PID控制器均出现较大波动,无法正常跟踪指令。而基于ESO的滑模控制器(即本文所设计的控制器)在外部强扰动作用下,依然具有很好的控制效果,可以同时满足瞬态响应和跟踪精度的需求。这说明本文设计的基于ESO的滑模控制器能够有效抑制复合扰动,具有较强的鲁棒性。