基于IPSO的舰载机出动离场规划研究

刘玉杰, 崔凯凯, 韩 维, 李 樾

(1. 海军航空大学航空基础学院, 山东 烟台 264001; 2. 海军招收飞行学员工作办公室, 北京 100071; 3. 中国人民解放军92942部队, 北京 100161; 4. 中国人民解放军92728部队, 上海 200436)

0 引 言

舰载机作为航母最关键、最核心的攻防武器,其出动回收效率将直接影响整个航母战斗群的作战能力。目前,世界各航母强国均基于自身航母及航空保障装备性能,积极开展航母出动回收流程规划研究。航母从回收着舰[1]至再次出动之前,通常需要经历甲板转运、出入库、机务勤务保障[2]、武器挂载、出动离场等工序。出动离场作为舰面保障与离舰升空的衔接环节,对编队任务的执行效能有着直接影响。

针对舰载机出动离场流程,文献[3]设计了一种面向出动离场任务的T-Petri网模型,对不同的出动离场任务进行仿真,同时研究人员还研究了粒子群优化(particle swarm optimization, PSO)算法[4]在离场出动问题上的应用。文献[5]将出动离场规划问题分解为起飞位选择和各起飞位上的舰载机排序两个阶段决策过程,分别设计了规划决策规则和自动规划方法。Liu等[6]将舰载机出动建模为混合流水车间规划问题,考虑了航母甲板上多架舰载机滑行协同轨迹规划问题,基于预设的舰载机出动离场滑行路径库,设计了一种双层遗传算法对问题进行求解。苏析超等[7]同样将出动离场过程建模为混合流水车间规划问题,并设计了一种混合差分进化算法,通过规划舰载机飞行前准备作业过程中多阶段工位上作业的保障顺序,提升了舰载机的出动效能。万兵等[8]进一步在混合流水车间规划模型的基础上,引入了间隔变量和逻辑约束,建立了一种约束规划模型,设计了一种多机出动离场规划启发式规则,将多机规划问题转化为单机规划问题,并提出一种单机约束引导启发式搜索与约束规划二分法迭代算法对舰载机出动离场流程进行优化。此外,研究人员还分析了起飞位对舰载机出动离场效能的贡献问题。

PSO算法是一种较为常用的智能优化算法[9],具有概念简单、所需调节参数少等优势[10],其在任务资源分配[11-12]、航迹规划等[13]领域都有着广泛的应用。但标准的PSO算法收敛精度较低且容易陷入局部最优,针对标准PSO算法的不足,学者们进行了相应的改进。文献[14]将混沌优化思想与PSO算法相结合,对粒子群的最优位置进行了混沌优化,提高了PSO算法跳出局部极值的能力。文献[15]通过将自适应策略与精英学习策略引入标准PSO算法,有效地提高了算法跳出局部最优的能力。文献[16]的并行免疫PSO算法利用免疫算子克服了PSO算法的局部收敛问题。

研究人员虽然对舰载机出动离场规划问题进行了一定的研究,但出动离场规划问题约束较为复杂且存在路径干涉问题,相关规划算法的优化性能仍存在进一步提升的可能性。本文设计了一种改进的PSO(improved PSO, IPSO)算法,该算法通过在参数自适应PSO算法的基础上引入基于莱维飞行扰动的模拟退火(simulated annealing, SA)机制,以提高PSO的局部搜索能力。将IPSO用于出动离场规划问题,取得了良好的规划效果。

1 舰载机出动离场规划模型

1.1 舰载机出动离场问题描述

舰载机位甲板负责完成机务勤务保障和武器挂载任务,飞行员接受任务登机后,舰面指挥规划转入出动离场阶段[17]。舰载机在执行出动离场任务时,需要按以下5个步骤执行任务,如图1所示。

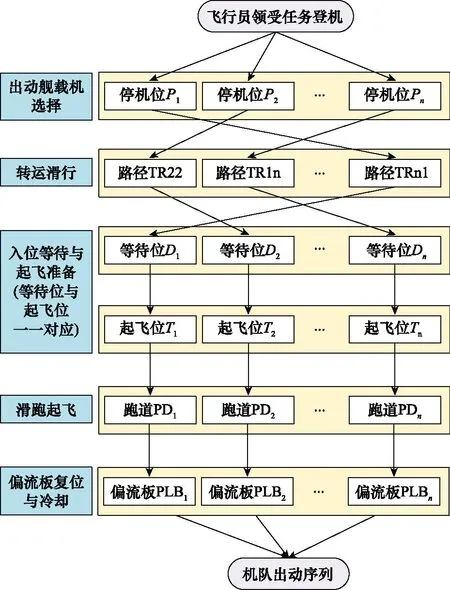
图1 舰载机机队出动流程示意图Fig.1 Schematic diagram of carrier aircraft fleet dispatch process

(1) 出动舰载机选择

通常甲板上停放的舰载机数量多于需要出动的舰载机数量,因此在制定出动计划之前需要选择执行出动任务的舰载机(或其停机位置)。同时,发动机在起飞出动前需在其停机位上完成暖机工作,本文假设出动前舰载机均已完成发动机暖机,且暖机时舰载机处在低速运行状态,忽略其对舰面设备的干扰[18]。

(2) 转运滑行

当舰载机完成暖机后,需要根据出动方案滑行进入相应的等待位或起飞位,为后续离场做准备。在该阶段需要考虑不同舰载机转运路径之间可能存在的干涉情况,制定避碰规则。

(3) 入位等待与起飞准备

当舰载机所分配到的起飞位有前序出动舰载机时,需要先滑行至偏流板后方的起飞等待位处,待前序舰载机出动起飞和偏流板冷却完毕后再滑行至起飞位进行起飞准备。当舰载机进入起飞位后,飞行员和舰面保障人员将会对舰载机执行最后的检查工作。

(4) 滑距起飞

当保障人员和飞行员检查舰载机完毕,确定无故障隐患后,将信息反馈给起飞助理员,起飞助理员检查起飞跑道并确认其满足起飞要求后给出起飞指令,飞行员在相应的跑道上完成起飞。

(5) 偏流板复位与冷却

舰载机完成起飞后,偏流板需要复位并冷却,待该工序结束后,单架舰载机的起飞离场阶段结束。

1.2 舰载机出动离场数学模型

在建立舰载机机队的出动离场模型前,根据问题实际做出如下假设:① 对于单架舰载机,其起飞离场各作业子阶段不可中断;② 忽略转运滑行子阶段的随机影响因素,默认转运时长只与转运路径的距离有关;③ 当不同的舰载机在转运过程中存在碰撞风险时,则两机的转运任务不能同时进行(需待前机转运完成后,后机的转运任务才能开始);④ 转运方案中,各机的暖机时间和起飞准备时间均设定为定值。

1.2.1 数学符号及其含义

Ej:待出动舰载机集合;

nj:待出动舰载机数量;

Ei:舰载机出动工序集合;

ni:舰载机出动工序数量;

Li:工序i可操作位置的集合;

j:舰载机编号,j=1, 2, 3,…,nj;

i:出动流程工序编号,i=1, 2, 3,…,ni;

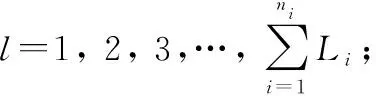
np:停机位数量;

P:停机位编号,P=1, 2, 3,…,np;

T:起飞位编号,T=1, 2, 3;

D:等待位编号,与起飞位一一对应,D=1, 2, 3;

PD:跑道编号,与起飞位一一对应,PD=1, 2, 3;

PLB:偏流板编号,与起飞位一一对应,PLB=1, 2, 3;

TRPD:从停机位P到起飞位T的转运路径;

ΔtPD:从停机位P到起飞位T的转运时间;

tN:暖机所需时间;

tZ:起飞准备时间;

ΔTf:同一停机位上先后两架飞机的起飞时间最小间隔(由舰载机尾流间隔、偏流板复位及冷却时间决定);

ΔTt:同一停机位先后被两架飞机使用且能够确保安全的最小间隔时间;

dsafe:转运过程中不同飞机之间必须要满足的安全距离间隔;

Bji:舰载机j的第i个工序的开始时刻;

DTji:舰载机j的第i个工序的最短执行时长;

Eji:舰载机j的第i个工序的结束时刻;

1.2.2 目标函数与决策变量

本文中,舰载机机群出动调度问题的决策变量为

考虑到舰载机机群出动任务所用时间越少,其后续回收保障任务可以越早开始,本文中所选择的目标函数为最小化出动完成时间,即

(1)

1.2.3 舰载机出动模型约束

(1) 对于某架舰载机j的任意一个工序i,其必须选择且只能选择一个操作位置执行,即

(2)

(2) 对于某架舰载机j的任意一个工序i,其完工时刻不小于该工序的开始时刻与工序最短执行时长之和,即

Eji≥Bji+DTji,∀i∈Ei;∀j∈Ej

(3)

(3) 对于某一操作位置,其任意时刻最多只允许一个工序在该位置执行,即

(4)

(4) 在甲板布列选择阶段,也即出动工序1阶段,单个停机位最多只能停放一架舰载机,即

(5)

(5) 对于某架舰载机而言,除工序1,其他工序的开始时间应满足如下关系:

Bji≥Ej(i-1)≥Bj(i-1)+DTji,i>1

(6)

(6) 对于某架舰载机,其转运滑行与入位等待工序之间的时长间隔必须超过转运耗时,即

Bj3-Bj2≥ΔtPD, TRPD,j=1

(7)

(7) 同一个起飞位前后两架舰载机的放飞时间间隔必须满足舰载机尾流间隔、偏流板复位及冷却时间限制,即

|Bj5-Bh5|≥ΔTf,∀l∈L5;WPj5,l=WPh5,l

(8)

(8) 一旦舰载机i的起飞位在工序3中被确定,则其工序4和工序5的执行位置也被确定,且与起飞位保持一致,即

WPj3,l=WPj4,l=WPj5,l,∀j∈Ej

(9)

(9) 对于某一个停机位,当舰载机进入该停机位时,前序舰载机已经从停机位离开,且时间间隔大于最小安全间隔时间,即

Eh3-Bj3≥ΔTt,∀l∈L3;WPj3,l=WPh3,l;Bj3>Bh3

(10)

(10) 对于某一个起飞位,当舰载机进入该起飞位对应的停机位时,前序舰载机已经离场,且偏流板已完成复位冷却,即

Ej3>Eh5,∀l∈L5;WPj5,l=WPh5,l;Bj5>Bh5

(11)

(11) 为保证转运安全,文中默认舰面转运过程是不可中断的,即某机的转运过程一旦开始,就要按预先的转运路径转移至预定的等待位上,即

(12)

(12) 在第2阶段的转运滑行过程中,在不同舰载机的转运路径之间要防止发生碰撞,即

(13)

1.2.4 舰载机滑行避碰策略

一般情况下,当任务要求出动的舰载机数量较多时,飞行甲板上会出现多架舰载机同时滑行的情况,而飞行甲板空间相对狭小,在进行多架舰载机同时滑行操作时必须要考虑避碰问题,本文采用如下避碰策略:

(1) 采用文献[19]中的牛顿保辛伪谱(Newton symplectic pseudospectral, NSP)法计算离线转运路径库,该路径库包括了从某停机位滑行至所有准备位的路径轨迹及时间点信息。

(2) 根据机群出动任务规划模型,获得机群出动方案,该方案包括了所有舰载机出动流程工序的先后顺序以及对应的加工位置序号。

(3) 根据从停机位滑行至起飞准备位工序的加工顺序,基于NSP-Dubins-相对速度障碍(reciprocal velocity obstacle, RVO)协同路径规划方法依次更新各架舰载机的实际路径和到达时间。具体步骤如下:

1) 对于优先级排序为K(优先级K由舰载机在出动方案中的顺序决定)的舰载机,假设其按照预规划的路径以及滑出时间开始滑出;

2) 获取当前时刻(优先级排序为K的舰载机开始滑出的时间)正在执行从停机位滑行至起飞准备位工序的工件(舰载机)数量以及各自的位置、姿态、速度;

3) 采用文献[6]中的避碰策略处理舰载机转运滑行阶段可能会出现的路径干涉问题,其主要思想是:依据离线路径库和转运滑行开始时间检测当前滑行的舰载机是否会与其他舰载机发生碰撞。若无碰撞风险,则甲板上正在转运滑行的舰载机均按照离线路径库以及原方案滑行;若存在碰撞风险,则记录甲板上正在转运滑行的舰载机的起始状态及其目标滑行的终点位置,保证滑行优先级最高的舰载机仍按照原方案计划的时间滑出。对当前甲板上正在滑行的全部舰载机进行协同路径规划,得到考虑避碰条件下舰载机的滑行路径以及到达时间,更新出动方案中舰载机的实际滑行路径以及滑行结束时间。

2 基于莱维飞行的IPSO算法

2.1 编码形式

考虑到本文所研究的舰载机出动离场规划问题可以抽象为一个带有动态干扰约束的混合流水车间规划问题,流水车间规划问题中必须要确定每个工件所对应工序的加工先后顺序,以及各个工序所对应的加工机器。因此,编码的形式在能够表示式(2)～式(13)中全部决策变量信息的前提下应尽量简洁且利于优化算法的处理操作。本文采用连续编码矩阵的形式来表示舰载机机群的出动回收规划方案,对于单架舰载机的出动离场规划问题,其编码的具体表示形式如图2所示。

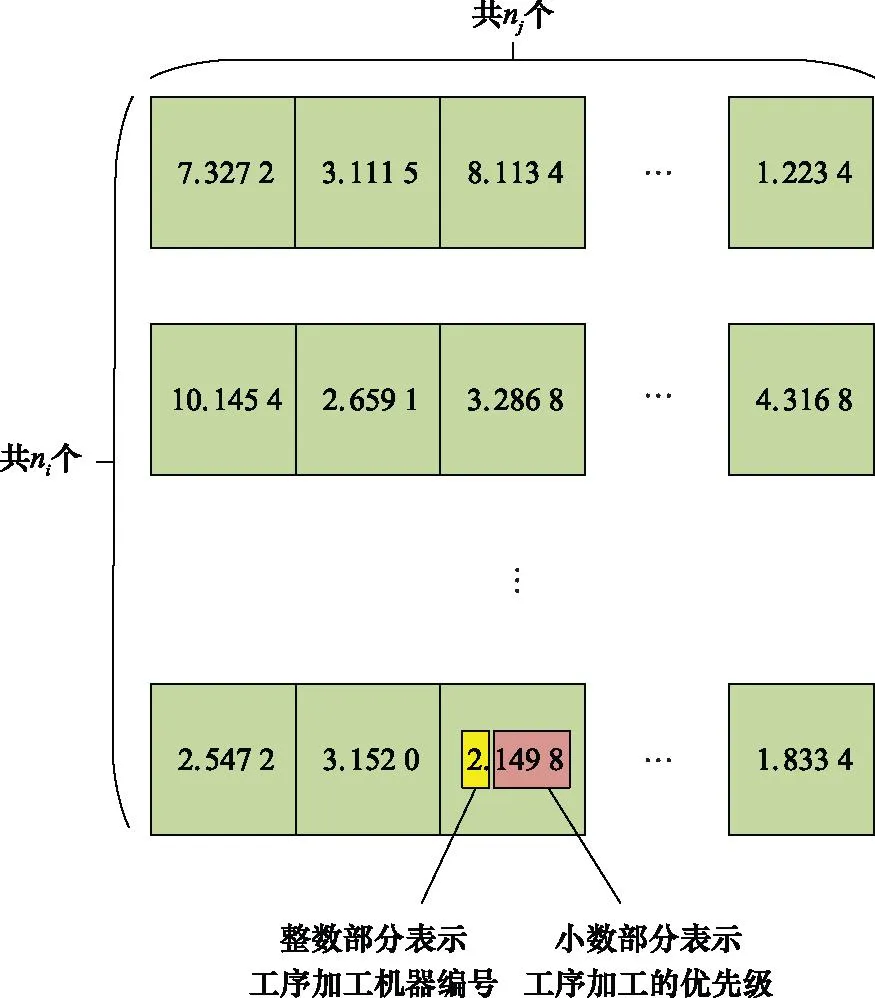
图2 编码矩阵示意图Fig.2 Schematic diagram of coding matrix

2.2 编码约束

由于在实际出动离场问题中存在流程及资源约束,采用图2中所示的编码形式时,必须要对编码基因进行如下的限制,以生成合理可行的编码方案。

(1) 编码的整数部分必须小于该工序的可用加工机器数量,以保证出动方案中的加工机器存在。

(2) 工序3～工序5的加工机器应一一对应。

根据编码中未完成工序的优先级生成待执行工序队列,从队列中按顺序选择待加工工序,判断是否满足式(2)～式(13)的约束条件。若满足则执行该工序,若不满足则按队列顺序选择执行下一工序,直至全部工序执行完毕,得到最终的出动离场执行方案,并计算离场任务完成时间。

2.3 IPSO算法

考虑到经典的PSO算法的寻优策略适应能力不强且缺乏局部寻优机制,本文基于莱维飞行公式和SA思想对经典的PSO算法加以改进,并将IPSO算法用于舰载机的出动离场规划问题。

2.3.1 标准PSO算法

标准PSO算法[19]的主要思想为:在整个D维寻优空间中随机生成一组(共m个)粒子,粒子i在寻优空间中的位置向量为Xi(0)=[xi1,xi2,…,xiD]T,速度向量为Vi(0)=[vi1,vi2,…,viD]T,粒子利用个体极值和种群极值信息在寻优空间中进行飞行,其飞行速度和空间位置更新如下:

(14)

式中:i∈[1,m],d∈[1,D];w为惯性权重系数,c1和c2为学习因子;r1和r2为[0,1]区间内的随机数;n为粒子群迭代次数;Pi=[Pi1,Pi2,…,PiD]为粒子i的历史最优位置,即个体极值点;Pg=[Pg1,Pg2,…,PgD]表示整个粒子群的历史最优位置。

2.3.2 参数自适应

从式(14)可以看出,在标准的PSO算法[20]中,参数w、c1和c2的值对粒子的运动行为会有较大影响,而标准PSO算法中的参数均设置为常数,不利于调整粒子的运动趋势。为此,本文借鉴文献[21]中的控制参数自适应思想,对参数w、c1和c2引入如下的自适应规则:

(15)

式(15)的主要作用是在算法的前期增加粒子飞行的全局遍历能力,而在算法的后期提升粒子的局部搜索能力。下标max、min分别表示对应变量的最大值和最小值。

2.3.3 基于SA和莱维飞行的邻域搜索机制

除了对标准的PSO算法进行参数自适应设置,本文基于莱维随机飞行和SA机制设计了一种粒子邻域搜索机制,以进一步增强算法的寻优性能,其主要思想在于将莱维飞行搜索机制优秀的邻域搜索能力应用到SA算法的邻域搜索中。

首先引入SA的概念[22],SA是一种基于蒙特卡罗思想的启发式随机寻优算法。其通过模拟固体降温的热力学过程,利用Metropolis准则的概率突跳特性在寻优过程中跳出局部最优解。徐小琴等[23]在利用布谷鸟搜索算法对电力系统资源进行优化配置的过程中,引入了SA机制来提高算法的全局和局部搜索能力。此外,SA算法在用户任务卸载[24]、导引车任务分配[25]以及旅行商等问题[26]中也取得了良好的效果。Metropolis准则的核心思想是在温度下降的过程中能以一定的概率接受较差的解,即在不同的情况下,算法对于新解的接受概率为

(16)

式中:E(x)表示能量值(也即适应度值);xold和xnew分别表示扰动前和扰动后的解;Temp表示退火温度。

本文采用莱维飞行对粒子进行扰动,莱维飞行的随机步长满足莱维分布,而莱维分布属于厚尾分布,其与Gauss分布相比尾翼更宽,扰动能力也更强[27]。当前,莱维飞行策略已经被广泛应用到各种寻优算法中。文献[28]针对风电场中的风机涡轮布局优化问题,设计了一种基于莱维飞行的野草(Levy flight invasive weed optimization, LFIWO)算法。文献[29]设计了一种基于莱维飞行的改进樽海鞘(Salp-Swarm)特征选择算法。Zhang等[30]将莱维飞行应用到双种群果蝇优化算法中,也取得了良好的效果。莱维随机步长依靠计算机编程语言实现时,一般采用Mantegna公式[31]:

(17)

式中:s表示莱维飞行的步长;参数β通常取为1.5;μ和ν为随机变量,满足正态分布:

(18)

式中:δμ和δν满足

(19)

式中:Γ为标准Gamma函数。

800代莱维飞行的随机路线如图3所示。

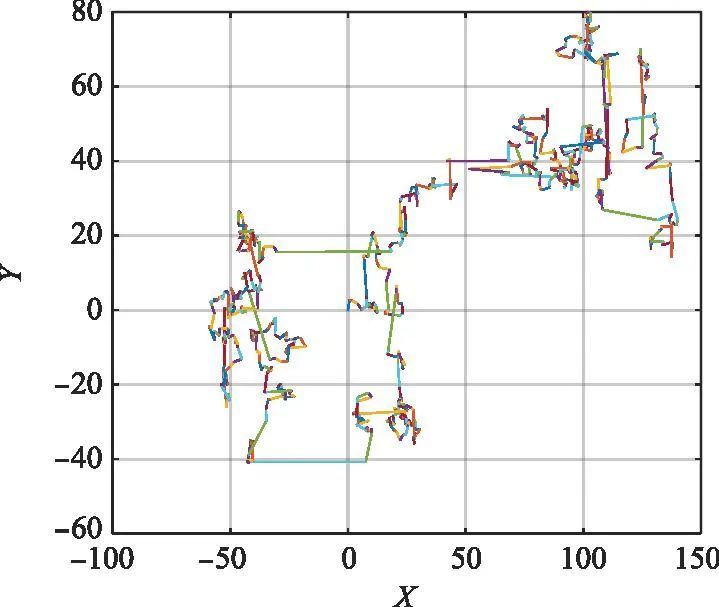
图3 800次莱维飞行路线图Fig.3 Routes of 800 times Levy flight

在粒子群的第k次迭代过程中,粒子Xi(k)=[xi1,xi2,…,xiD]T经过莱维飞行扰动后变为

(20)

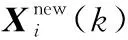
3 仿真实例分析

3.1 仿真条件设置

以某弹射型航母的出动离场任务作为仿真案例,该航母共有3个起飞位可用,编号分别为A、B、C,航母的甲板布置如图4所示。1～13号停机位至A、B、C后方的起飞等待位的转运路径,以及起飞等待位至相应起飞位的转运路径均已提前通过计算获得,并储存在转运路径库中,出动过程中各机的转运路线均从转运路径库中选择。基于文献[6]中的避碰策略处理舰载机转运滑行阶段的路径干涉,待出动的舰载机类型相同,且认为均已完成舰面保障工作。

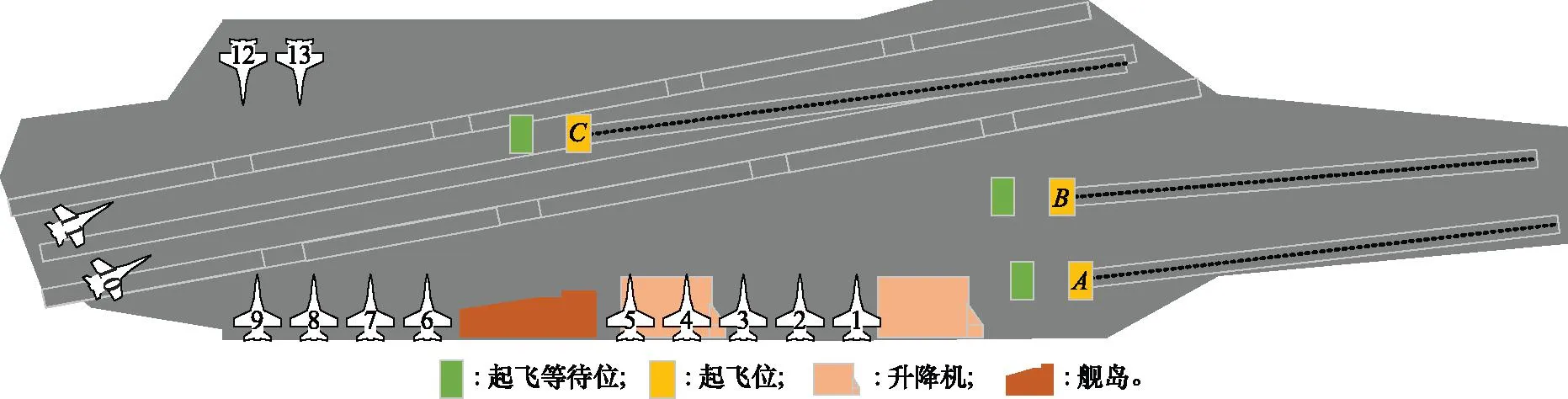
图4 算例航母甲板布置示意图Fig.4 Deck layout schematic diagram of example aircraft carrier

设置IPSO的种群规模为50,最大的迭代次数为50,莱维飞行的扰动尺度因子设为0.2。自适应参数的取值为c1max=2.5,c1min=1.25,c2max=2.5,c2min=1.25,wmax=0.9;wmin=0.15;扰动尺度因子θ=0.2。

仿真环境为Windows 10操作系统,采用Matlab 2016b仿真软件,仿真平台为8 G内存、主频2.30 GHz的PC机。

3.2 仿真结果及对比

首先,给出共有8架舰载机进行出动的条件下,采用IPSO算法进行离场规划时所得到的舰载机离开停机位的出动顺序,即1→7→2→13→6→10→5→4,其出动工序完工时间为389.7 s,算法求解时长为207.74 s,出动方案甘特图如图5所示。

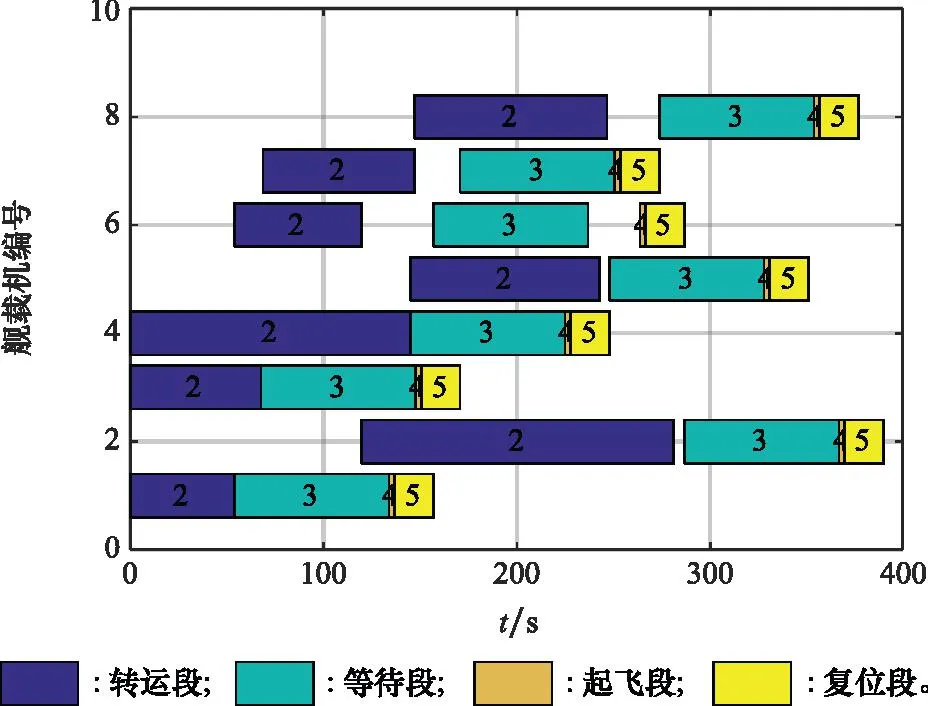
图5 8架机出动方案甘特图Fig.5 Gantt chart of eight aircraft’s deployment plan

甘特图中的数字表示舰载机出动过程中的子工序编号,由于工序1为出动舰载机选择,属于虚拟工序,所以此处仅给出了工序2～工序5的加工时间情况。

出动舰载机数量规模为8架时,各个加工位置的工序占用时间甘特图如图6所示。其中,甘特图中的数字表示舰载机的编号及其工序编号,如“603”表示舰载机6的第3道子工序。

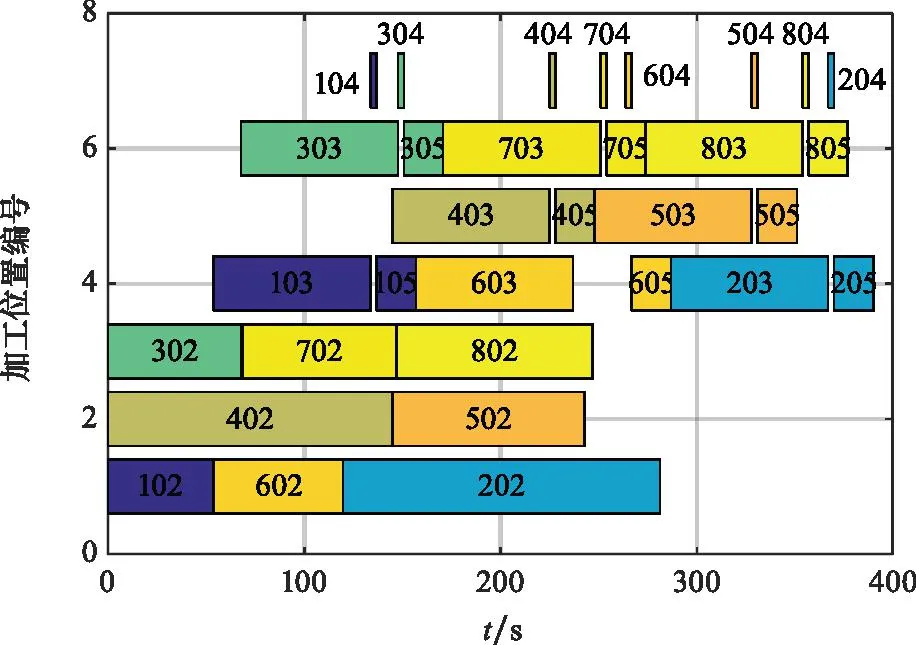
图6 8架机出动时加工位置的使用情况甘特图Fig.6 Gantt chart of the processing positions working when eight aircraft are dispatched

为了验证算法的效果,这里选择文献[6]中的双层编码遗传算法(double-layer coding genetic algorithm, DL-GA)进行对比,当出动舰载机数量规模为8架时,IPSO算法与DL-GA算法的迭代收敛曲线对比图如图7所示。

图7 8架机出动迭代曲线对比图Fig.7 Comparison diagram of iteration curve when eight aircraft are dispatched

从图7可以看出,采用本文所提IPSO算法可以显著提高舰载机的出动效率。与文献[6]中的算法相比,在有8架舰载机出动的情况下,采用本文所设计的IPSO算法优化得到的出动方案完成时间比文献[6]中算法的出动完成时间减少了32.9 s。

3.3 不同出动规模条件下的仿真结果

考虑舰载机出动规模增加时算法的规划效果,假设出动的舰载机数量规模增加至10架,采用IPSO算法得到的出动方案如图8所示。在所得到的出动方案中,各舰载机出动的顺序为13→2→5→3→4→9→11→6→12→7,其出动工序完工时间为490.3 s。

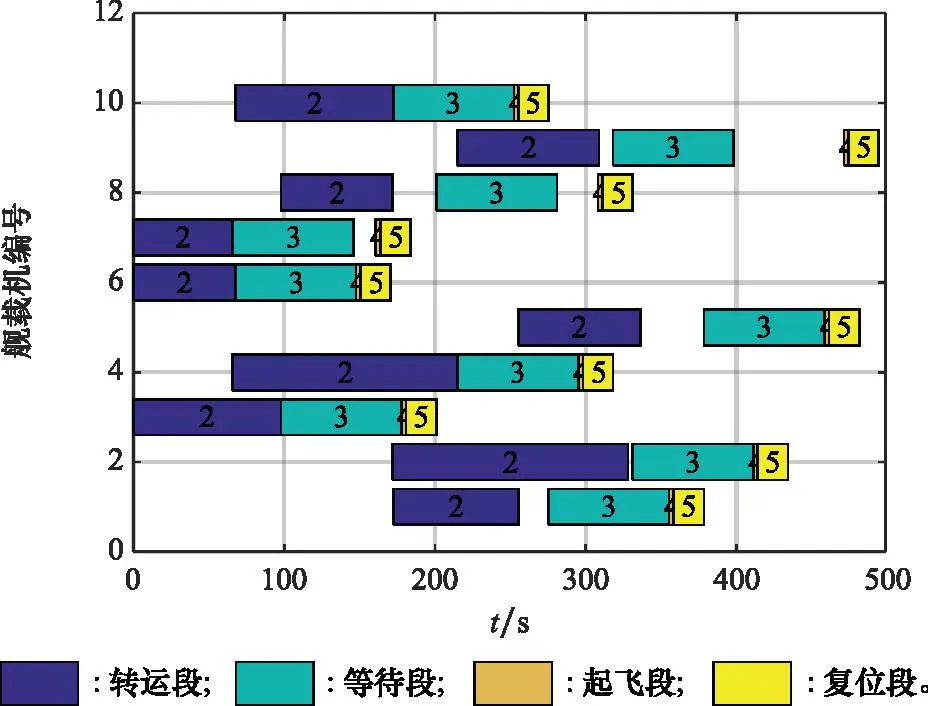
图8 10架机出动方案甘特图Fig.8 Gantt chart of 10 aircraft’s deployment plan

当出动舰载机数量规模为10架时,各个加工位置的工序占用时间甘特图如图9所示。

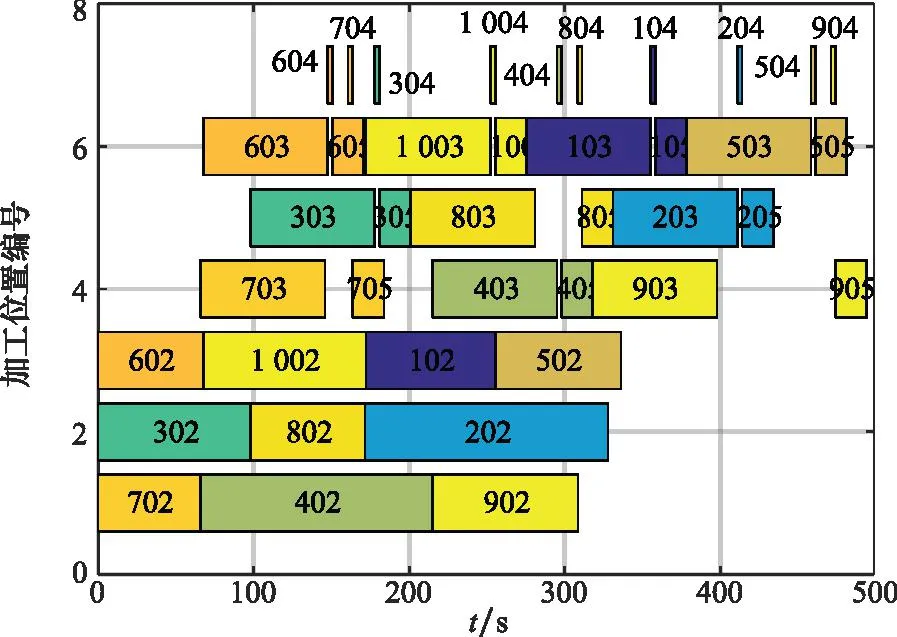
图9 10架机出动时加工位置的使用情况甘特图Fig.9 Gantt chart of the processing positions working when 10 aircraft are dispatched

当出动舰载机数量规模为10架时,算法的迭代收敛曲线如图10所示。

图10 10架机出动方案迭代曲线Fig.10 Iteration curve of 10 aircraft’s dispatching plan

进一步,当所需出动的舰载机数量为12时,采用IPSO算法得到的出动方案如图11所示。在所得到的出动方案中,各舰载机出动的顺序为6→1→7→3→9→5→11→8→4→2→12→13,其出动工序完工时间为587.5 s。

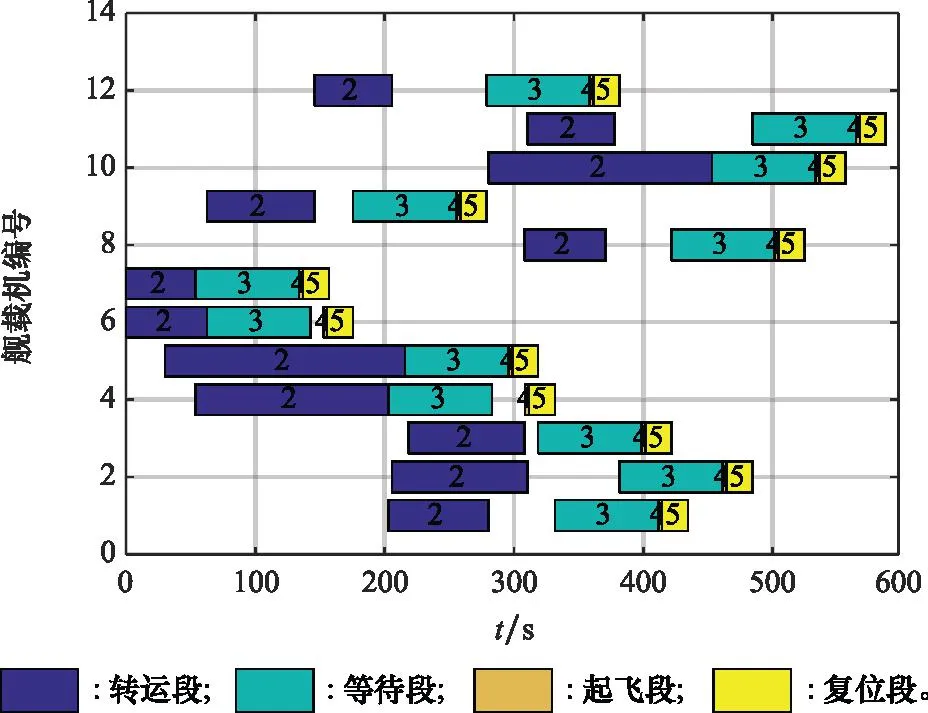
图11 12架机出动方案甘特图Fig.11 Gantt chart of 12 aircraft’s deployment plan

当出动舰载机数量规模为12架时,各个加工位置的工序占用时间甘特图如图12所示。

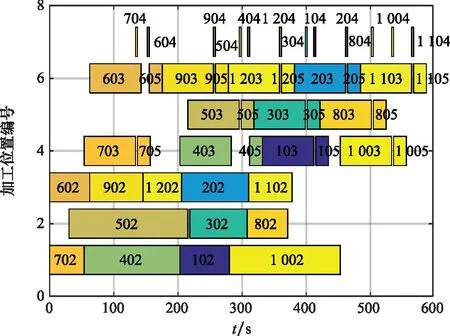
图12 12架机出动时加工位置的使用情况甘特图Fig.12 Gantt chart of the processing positions working when 12 aircraft are dispatched

当出动舰载机数量规模为12架时,算法的迭代收敛曲线如图13所示。

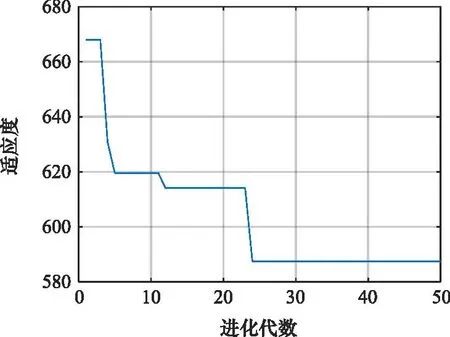
图13 12架机出动方案迭代曲线Fig.13 Iteration curve of 12 aircraft’s dispatching plan

当舰载机出动规模分别为10架和12架时,算法的仿真计算时长分别为319.33 s和414.05 s。据此可以计算,当舰载机数量分别为8、10、12时,算法中种群进化一代所需要的计算时长分别为4.15 s、6.39 s和8.28 s。由此可见,当舰载机数量增加0.5倍后(由8增加至12),其单代进化耗时增加近1倍。

4 结束语

本文针对舰载机出动离场规划问题提出了一种IPSO算法,该算法通过在参数自适应粒子群算法的基础上引入基于莱维飞行扰动的SA机制来提高标准PSO算法的局部搜索能力。与已有文献中的DL-GA算法在同条件下进行仿真对比,仿真结果表明本文所提出的IPSO算法较DL-GA算法而言具有更好的寻优效果。

但本文假设出动前舰载机均已完成发动机暖机,且暖机时舰载机处在低速运行状态,可忽略其对舰面设备的干扰。后续将进一步把暖机对舰面设备的干扰考虑在内,研究其对出动效率的影响,以及如何进一步提高出动效率。此外,本文当前仅针对有人舰载机模式进行了研究,为有效应对当前人工智能高速发展趋势,后续将梳理舰载无人机甲板出动流程,并针对有人/无人机协同出动离场和无人机机群出动离场规划特点,对该算法做出适应性改进研究。