面向韧性的指挥信息系统节点重要性度量方法

岳地久, 李建华, 王 哲

(1. 空军工程大学信息与导航学院, 陕西 西安 710077; 2. 中国人民解放军94755部队,福建 漳州 363000; 3. 国防科技大学信息通信学院, 湖北 武汉 430010)

0 引 言

指挥信息系统是以计算机网络为核心,包含指挥控制、情报、通信、信息对抗、综合保障等分系统,对作战信息进行实时获取、传输、处理,用于保障各级指挥机构对所属部队和武器实施科学高效的指挥控制的军事信息系统[1]。指挥信息系统既是信息化条件下体系作战的核心和中枢,也是被攻击的首要目标之一,指挥信息系统一旦被精确打击导致节点损毁,将影响其功能运行,很有可能造成指挥中断、战场失利等严重后果。在军事领域,近些年来,国际上提出了Resilience一词,国内部分学者将其译为“韧性”。“韧性”是指系统遭受攻击后,功能受损、性能下降,在经过相应恢复手段后,系统仍然能够完成任务[2]。指挥信息系统的韧性决定了其承受攻击并迅速从攻击中恢复的能力,吸引了大量学者的关注[3-5]。指挥信息系统韧性依赖于系统的结构和节点,而且各个节点对系统韧性的影响也不同。为增强指挥信息系统韧性,使资源使用效费比最大,必须把有限的资源投入到对系统韧性影响最为显著的节点上,因此分析各个节点对系统韧性到底有多大的影响,也就是面向韧性的节点重要性度量,就变得尤为迫切。

目前,有关复杂系统节点重要性的度量已被广泛地研究与应用,其方法大致可分为三类:一是基于复杂网络的方法[6-7],运用节点在网络中的局部或全局结构信息来评估节点重要性,如:度中心性、接近中心性、介数中心性等各类中心性指标[8-9],以及k-shell方法[10]、节点删除法[11]、信息熵法[12-13]等。二是多属性决策方法[14]。为克服运用节点单一属性的局限性,部分学者提出运用节点的多个属性,从不同角度综合度量节点重要性[15-16]。三是基于功能水平贡献率的方法,运用节点对系统各类功能发挥的贡献程度来度量节点重要性,如文献[17]提出基于装备体系韧性增加值的作战网络链路重要度评估方法,文献[18]提出基于作战功能贡献度的网络化防空节点重要性评价方法。以上三类方法在评估节点重要性时,基本遵循“显著性等于重要性”或者“破坏性等于重要性”的原则来对节点进行重要性排序。

此外,还有学者借鉴可靠性工程研究方法,提出基于韧性的系统组件重要度评估方法[19],运用组件性能改变对系统韧性的影响程度来定义组件的重要性。Pan等[20]定义了基于韧性的体系组件重要度,从事前、事中和事后三个角度提出组件韧性重要度。Li等[21]提出了基础设施系统的7种基于韧性的组件重要度计算方法。

现有这些研究都是在系统结构和相关特征数据的基础上开展的,针对韧性的节点重要性研究尚不多见。以上这些方法虽然能够为指挥信息系统节点重要性度量提供一定的参考借鉴,但对于指挥信息系统韧性而言,这些评估方法所定义的重要节点是否对系统韧性的增强也存在关键作用,目前尚未证实,还有待深入研究。此外,指挥信息系统鲜明的军事属性,也决定了其面向韧性的节点重要性度量方法有别于复杂网络、基础设施系统等。另外,如果指挥信息系统在建模过程中未采用复杂网络模型,那么上述第一类方法也就不再适用。

为解决上述问题,本文提出一种面向韧性的指挥信息系统节点重要性度量方法。这里研究的指挥信息系统,主要指由各级各类指挥控制系统、情报处理系统、武器控制系统等依托共用信息基础设施网络化连接,保障指挥员对所属作战力量实施指挥控制的军事信息系统;这里研究的指挥信息系统节点,主要指地理上相对分散、功能上相对独立的各类指挥信息系统组成部分,如区域控制中心的指挥所系统、雷达旅指挥所系统、地导营指挥所系统、雷达站情报处理系统等。本文定性分析了指挥信息系统韧性过程,提出指挥信息系统韧性定量计算方法;基于各个节点韧性增加/减少相同比率对系统韧性的影响程度来度量节点重要性,并运用蒙特卡罗仿真方法计算节点重要性;通过单调性和肯德尔相关系数来评价该方法的性能。

1 指挥信息系统韧性过程和度量

指挥信息系统在战场上容易受到攻击,确保其安全、可靠运行关系重大。因此,针对指挥信息系统的可靠性、抗毁性、鲁棒性以及韧性等研究相继展开,其中韧性综合体现了系统抗干扰能力和恢复能力,能够全面地表征系统抵抗攻击、受损降级、适应攻击、快速恢复的过程,成为近年来的研究热点。

指挥信息系统功能水平在攻击前后的变化过程如图1所示。

图1 指挥信息系统韧性过程Fig.1 Resilience process of command information system

初始情况下(时间为0～t0),指挥信息系统预测潜在攻击并做好准备工作,功能水平保持正常,处于P0;t0时刻,攻击发生,系统在韧性作用下,功能水平变化过程可以分为降级和恢复两个阶段。

降级阶段(时间为t0～td):t0时刻,指挥信息系统遭受攻击,受损节点功能水平开始降级,有可能导致整个系统的功能水平也降级。过程中,系统需要抵抗攻击、吸收攻击并适应攻击,td时刻,系统功能水平降低至最低点P1。

恢复阶段(时间为td～t1):td时刻,指挥信息系统开始采取恢复措施,系统功能水平逐渐回升,直至到达初始状态,或者达到新的稳定状态(如图1中红色虚线和蓝色虚线所示)。t1时刻,系统恢复到稳定状态后,又进入一个新的周期,并继续做好预防下一个潜在攻击的准备。

指挥信息系统遭受攻击后降级(或恢复)过程中功能水平变化曲线可以表示为关于时间的函数,一般可用线性函数、指数函数或三角函数3种类型的函数来表达。降级过程中函数表达式[22]如下:

(1)

(2)

(3)

式中:f(t)为t时刻系统功能水平;ts为系统功能水平开始降级的时刻;tp为系统降级持续时长;a和b是根据数据统计和模拟仿真,经曲线拟合出的相关参数。同样,系统恢复过程中系统功能水平变化情况,也可用上述3种函数表达式表示。当表示恢复过程时,ts为系统功能水平恢复开始时刻,tp为恢复持续时长。

为分析指挥信息系统不同节点对指挥信息系统韧性不同的影响作用,首先需要对指挥信息系统韧性进行定量的计算。在现有研究中关于复杂系统韧性的定量计算中,不同学者根据研究目的和侧重点,提出了不同的方法,方法主要分为确定型度量和概率型度量两大类[23]。确定型度量方法多起源于美国多学科地震工程研究中心(Multidisciplinary Center for Earthquake Engineering Research, MCEER)提出的“韧性三角”理论[24],该方法反映了系统在确定型扰动情况下的韧性;而概率型度量方法反映了系统在随机扰动情况下的韧性。

为确保被攻击时,指挥信息系统仍能持续保障关键作战任务完成,系统应具备很高的韧性,也就是说系统应该在规定的时间内从受损状态恢复至可以保障任务完成的功能水平。这里应用确定型韧性度量方法来计算系统在一个确定的攻击i下的韧性值[25],具体为

(4)

式中:RA,i为系统在攻击i下的韧性;t0为攻击i发生的时间;Ta为系统规定的恢复时间(根据战场情况和实际需要设置);Qi(t)为攻击i发生后t时刻系统的功能水平;Q0(t)为系统受攻击前的初始功能水平,也可认为是系统在正常情况下的功能水平。

若对系统功能水平进行归一化处理,假设初始时刻系统功能水平为1,即Q0(t)≡1,则式(4)中分母的值为Ta。式(4)的物理意义为图1中系统功能水平曲线下斜线阴影的面积占该矩形面积的比例,表征了系统在攻击发生后在规定恢复时间内的系统平均功能水平。容易得到,RA,i∈[0,1]。平均功能水平越高,说明系统受到攻击i的影响越小,系统的韧性越强。通过引入规定恢复时间,可以用式(4)比较不同系统在不同攻击情况下相同时间内的韧性值。

考虑到指挥信息系统的多样性、所面临的环境的复杂性以及攻击发生的随机性,学者们提出了用概率型韧性度量方法来反映系统韧性的随机性。这里运用期望韧性和韧性概率来度量指挥信息系统的韧性[26],即

(5)

RP=Pr(RA,i≥R*)=1-F(RA)

(6)

式中:RS为指挥信息系统的期望韧性;Pi为攻击i发生的概率;I为总的攻击数量;R*为用户定义的韧性阈值;Pr(RA,i≥R*)为第i次攻击情况下系统韧性值大于韧性阈值的概率;F(RA)为攻击下系统韧性的累计概率分布函数。指挥信息系统韧性期望值反映了系统在随机攻击下的平均韧性值,概率韧性值量化了系统韧性在随机攻击下满足需求的概率。

2 基于韧性的指挥信息系统节点重要性评估

2.1 指挥信息系统节点建模

指挥信息系统根据网络中心化作战理念及信息流程,依托信息栅格对各类传感器系统、指控系统、武器系统等战场要素进行逻辑组网,形成了感知网络、指控网络、武器网络3个功能网络和1个物理网络[1](即信息栅格)。指挥信息系统网络中心架构模型[27]如图2所示。

图2 指挥信息系统网络中心架构模型Fig.2 Network centric architecture model of command information system

根据该模型,指挥信息系统在数学上可以用集合的形式表示为

S={S1,S2,S3,S4}

(7)

式中:S表示指挥信息系统;Si(i=1,2,3,4)分别表示感知网络、指控网络、武器网络和信息栅格。

Si(i=1,2,3,4)由更下一级的节点组成,若Si包含m个节点,则可表示为Si={Si1,Si2,…,Sim}。其中:

(1) 感知网络。主要由传感器节点、信息处理节点、信息服务节点和情报指挥节点构成,由各类节点组网连接,联合对战场目标实施探测、侦察、监视,进行统一的栅格化多源融合处理,形成全域一致的战场感知态势,实现情报感知、处理和用户节点的即插即用,按需共享。感知网络内包含大量由传感器节点、信息处理节点、信息服务节点构成的情报链路,定义一条情报链路的功能水平函数为

f1k(t)=f1kOr(t)·f1kPs(t)·f1kDu(t)

(8)

定义感知网络的功能水平函数为

(9)

式中:f1kOr(t)、f1kPs(t)、f1kDu(t)分别为第k条情报链路上的传感器节点Or、信息处理节点Ps、信息服务节点Du在时刻t的功能水平;K为感知网络内情报链路总的条数;wk为第k条情报链路的权重。

(2) 指控网络。主要由各级各类指控系统节点构成,大致可分为战略战役和战术两个层级。战略战役节点根据任务接入情报态势,实现协同决策和联合计划;战术节点根据上级节点的任务分配和指控信息,实现区域控制和行动指挥。指控网络内包含大量的上下级指挥关系,定义一对指挥关系的功能水平函数为

f2l(t)=f2lC2S(t)·f2lC2J(t)

(10)

定义指控网络功能水平函数为

(11)

式中:f2lC2S(t)、f2lC2J(t)分别为第l对指控关系上级和下级指控系统在t时刻的功能水平;L为指控网内所有指控关系的总数目;wl为第l对指挥关系的权重。

(3) 武器网络。主要由信息化武器节点构成,支持指控节点对武器节点的铰链控制,可实现复合瞄准、跟踪,接力指导,协同攻击。定义一个武器节点的功能水平函数为

f3q(t)=f3qAq(t)·f3qC2q(t)

(12)

定义武器网络功能水平函数为

(13)

式中:f3qAq(t)和f3qC2q(t)分别为第q个武器系统及其上级指控节点在t时刻的功能水平;Q为武器系统总数;wq为第q个武器系统的权重。

(4) 信息栅格。集合各种通信、计算、软件和信息资源,为感知网络、指控网络和武器网络提供一致的信息获取、处理和共享的信息环境,支撑3个功能网络耦合和铰链,实现情报—指挥—武器的集成。这里把信息栅格中各节点统一归类为通信节点。信息栅格内包含大量通信节点—通信链路—通信节点的信息传输链路,定义一条信息传输链路的功能水平函数为

f4p(t)=f4pCin(t)·f4plink(t)·f4pCout(t)

(14)

定义信息栅格功能水平函数为

(15)

式中:f4pCin(t),f4plink(t),f4pCout(t)分别为第p条通信链路信息发送端点、通信链路、信息接收端点的功能水平函数;P为通信网内通信链路的总条数;wp为第p条通信链路的权重。

指挥信息系统功能水平取决于各子网络的功能水平及耦合情况。指挥信息系统整体功能具有流结构特征和短板效应,这里定义指挥信息系统功能水平函数为

(16)

式中:θi为子系统i权重。

以上定义中的系统和节点的功能水平为[0,1]之间的无量纲值,与系统和节点在t时刻的性能状态构成映射关系,其取值为0时表示系统完全失效,取值为1时表示系统处于最佳状态[28]。

2.2 基于韧性的节点重要性分析

指挥信息系统节点具有异质性,每个节点在系统中发挥的作用并不相同,不同的节点对系统韧性的贡献率也不同。为增强指挥信息系统韧性,应该将有限的资源分配给对系统韧性有显著影响的节点上。因此,必须对节点的重要性进行评估和排序,以确定关键的节点,也就是基于韧性的节点重要性度量。引言部分提到的现有对节点重要性度量的研究,由于其各自的适用范围,并不适用于本文的应用场景。

要分析各个节点对系统韧性的影响,容易考虑到的方法是基于仿真计算的方法,通过对各节点韧性增加或者减少同一数值Δx,来观察各节点对系统韧性的影响。然而,指挥信息系统各个节点由于自身所处层级、所担负的功能、所面临战场环境等的不同,各个节点的初始韧性值也并不相同,那么要求其韧性增加或者减少相同数值Δx的难度也会千差万别。此外,在一种特殊情况下,节点i的韧性值为0.9,节点j的韧性值为0.1,现在要求两个节点的韧性增加或者减少Δx(Δx=0.1),一方面达成目标的概率大为不同,节点j韧性增加0.1相比节点i要容易得多;另一方面,若要求这两个节点的韧性值增加或减少Δx(Δx>0.1),两个节点的韧性值将超出[0,1]范围,问题变得没有意义。

这里借鉴其他领域节点重要性度量方法,定义指挥信息系统节点韧性重要性为在不同节点韧性值增加或者减少相同的变化率,即增加/减少β%时,对系统韧性值的影响程度。具体如下:

(17)

(18)

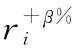
2.3 基于蒙特卡罗仿真的节点重要性计算

考虑到指挥信息系统的复杂性,以及攻击发生的随机性和攻击后系统恢复过程中的随机性,本文应用蒙特卡罗仿真方法对指挥信息系统韧性及节点重要性进行仿真计算。蒙特卡罗仿真步骤的具体说明如下,模拟仿真框架如图3所示。

图3 基于蒙特卡罗仿真的节点重要性计算框架Fig.3 Framework for node importance calculating based on Monte Carlo simulation

步骤 1初始化变量。主要定义如下参数:指挥信息系统功能水平函数,系统初始功能水平,每个节点被攻击的概率(攻击i),韧性过程中节点功能水平随时间变化的函数,节点韧性相关的参数分布(节点功能水平下降最大值Li,功能水平下降持续时间tde,i,功能水平恢复时间tre,i),以及系统规定的恢复时间Ta。

步骤 2蒙特卡罗仿真。设定仿真次数为N,计算指挥信息系统期望韧性,以及指挥信息系统在节点i韧性值增加/减少β%的情况下系统韧性值。每次仿真过程中的步骤如下。

步骤 2.1运用直接抽样法,抽样确定被攻击的节点i以及该节点韧性相关的3个参数Li,tde,i,tre,i。

步骤 2.2应用式(4)计算该次攻击下系统韧性值RA,j(r)。

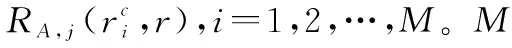
步骤 3应用式(5)计算指挥信息系统韧性。运用N次仿真的数据,计算系统初始韧性,以及各节点韧性增加/减少±β%后系统韧性值。

步骤 4基于韧性的节点重要性计算。通过式(17)和式(18)计算所有节点基于韧性的重要性,按照从大到小排序,即可得到节点重要性排序。

3 仿真实验与分析

3.1 条件假设与数据来源

为便于开展计算,作出如下假设。

假设 1攻击:每次只考虑一个节点遭受攻击。

假设 2依赖关系约束:将感知网络、指控网络、武器网络的节点视为功能节点,将信息栅格中的节点视为物理节点。每个功能节点与1个物理节点建立依赖关系,由于功能节点必须依赖于物理节点之间建立的通信链接才能发挥功能,因此当功能节点出现故障时,物理节点不受影响,而当物理节点出现故障时,考虑到通信约束,功能节点故障情况遵循如下规则:

(19)

假设 3功能水平下降:攻击发生在瞬间,造成的节点功能水平下降也发生在瞬间,功能水平下降呈垂直型。各个节点在遭受攻击时功能水平下降的最大值呈均匀分布:Li～U(0,Ci)。

(20)

恢复函数为指数函数时,其函数表达式为

(21)

恢复函数为三角函数时,其函数表达式为

(22)

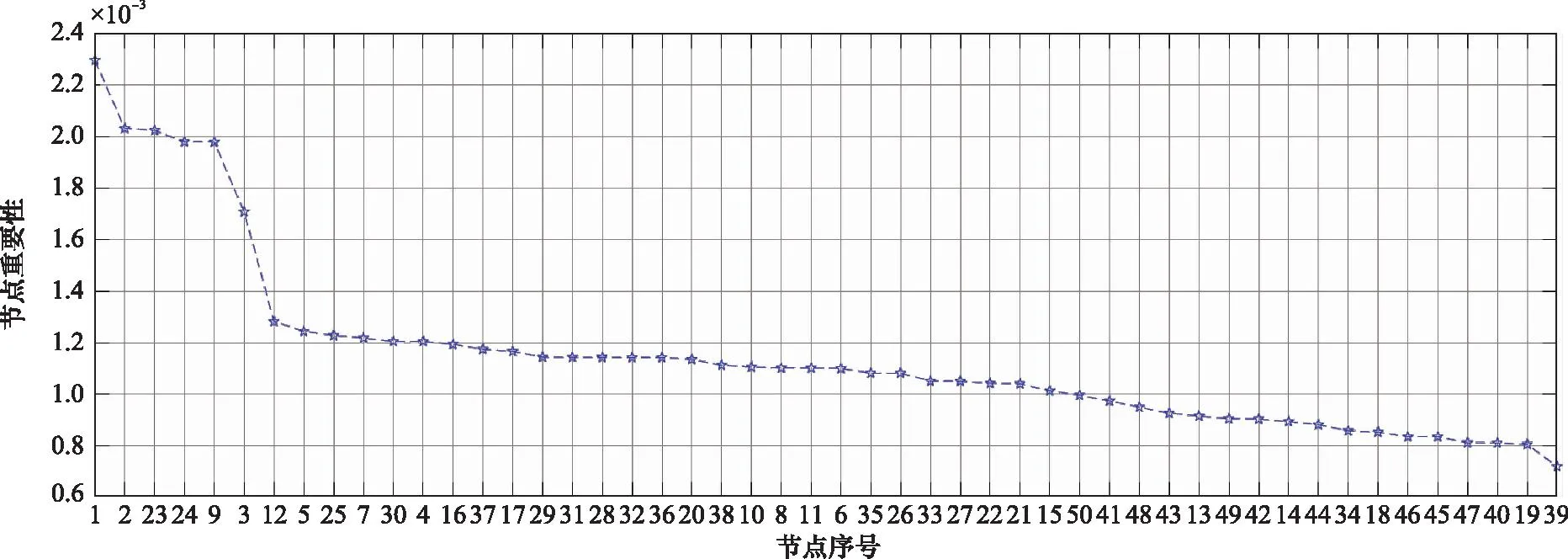
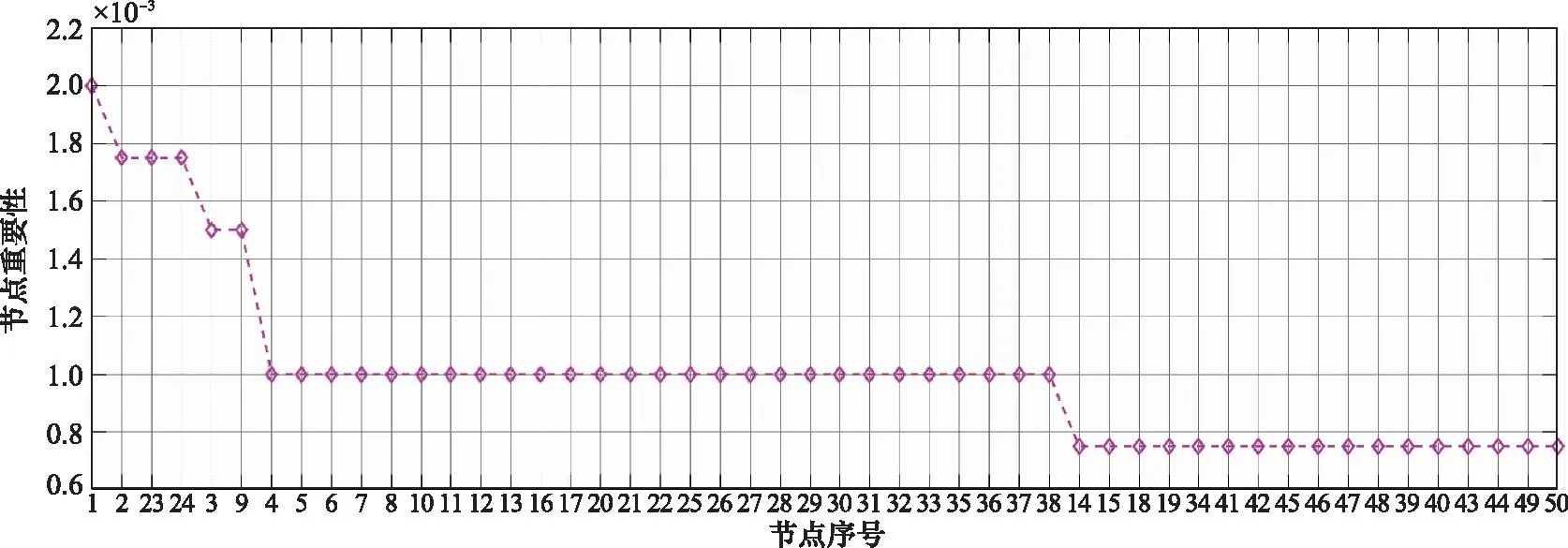
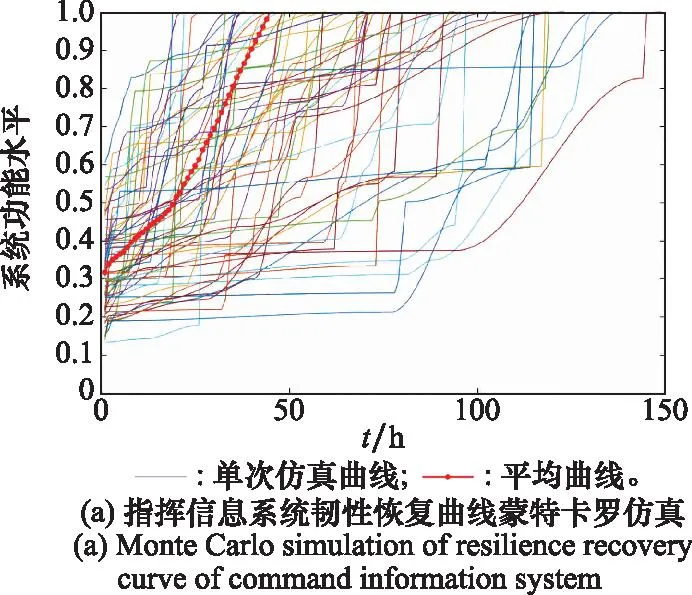
式中:fR,i(t)为t时刻节点ni的功能水平;Li为ni遭受扰动时最大降级(损失)值;t0,i为节点i被攻击的时刻,设t0,i=1;ci(t0,i)为ni初始功能水平;tde,i为节点ni降级持续时间,tde,i=0;tre,i为部件i恢复持续时间;t0,i+tde,i

其中,假设1是为了简化研究问题,同时也是韧性分析中常用的假设;假设2是因为要体现指挥信息系统中通信节点的基础支撑作用,也是基于相依网络建模的方法中常用的假设;对于指挥信息系统而言,面对攻击,每个节点的功能水平降级程度、降级时间和恢复时间均可量化,并服从一定的概率分布,可以通过大量数据统计得到。经过文献调研[30-32],均匀分布是随机流网络节点性能降级常用的分布,对数正态分布是常用的系统维修时间分布。因此,假设3中指挥信息系统节点功能水平降级服从均匀分布;假设4中节点功能恢复时间服从对数正态分布。

为进行仿真分析,假设一个包含50个节点的系统,其拓扑关系如图4所示(其中通信支持关系只标明4条,其他大部分略)。根据以上假设和相关资料,各节点韧性的相关数据如表1所示。设定F(t0)=1,fi(t0)=1,fij(t0)=1,即各权值均相等。

表1 仿真实验中指挥信息系统节点相关参数Table 1 Relevant parameters of command information system’s node in simulation experiment

图4 仿真实验中指挥信息系统拓扑关系示意图Fig.4 Topological relationship schematic diagram of command information system in simulation experiment

3.2 实验与结果分析

3.2.1 指挥信息系统韧性过程仿真

指挥信息系统节点若因遭受攻击导致其功能水平下降,也会影响到系统的功能水平。以节点3为例,假设t=0时系统遭受攻击,在3种形式的恢复函数下,节点3和指挥信息系统功能水平曲线如图5所示。图5(a)和图5(c)为节点3遭受攻击后,其功能水平在3种形式恢复函数下的功能水平曲线;图5(b)和图5(d)为节点3遭受攻击后指挥信息系统功能水平曲线;图5(a)和图5(b)为Ta>tre,i时节点和系统的韧性过程;图5(c)和图5(d)为Ta

图5 节点3遭受攻击后指挥信息系统韧性过程仿真Fig.5 Simulation of resilience process of command information system with node 3 attacked

3.2.2 基于韧性的指挥信息系统节点重要性度量

运用第2.2节提出的方法,根据各节点韧性值均增加β%=8%后对系统韧性的影响程度来度量节点重要性,结果如图6所示。由图6可知,节点1的重要性远高于其他节点,节点重要性排序为节点2、节点23、节点24,然后是节点9和节点3。其中,节点1为区域指控中心,节点2为区域情报中心,节点23和节点24为保障上述两个节点的通信枢纽,节点9和节点3分别是地导旅指挥所和雷达旅指挥所。评估结果与军事经验相符,说明本方法是有效的。

图6 基于节点韧性改变相同比率的指挥信息系统节点重要性排序Fig.6 Ranking of nodes importance of command information system based on node resilience changing the same ratio

3.2.3 基于韧性的节点重要性度量方法性能分析

学者们通常用单调性指标M(α)来评价节点重要性度量方法的分辨率[33],用肯德尔相关系数τ来评价方法的准确性[34]。

(1) 单调性分析

单调性的计算公式为

(23)

式中:α为由节点重要性度量方法得到的排序结果向量;M为节点总数;nr为重要性值为r的节点数量;M(α)∈[0,1],M取1时,结果向量α完全单调,说明该方法能够完全区分系统中所有节点的重要性;M取0时,则完全无法区分。

文献[25]定义体系中部件的结构韧性重要度计算方法为

(24)

式中:n是系统中的部件数;Wi=1为部件i的正常状态;Wi=0为部件i的失效状态;RP(j,Wi=1),RP(j,Wi=0)分别表示在部件i正常/失效状态下,系统其他节点受到扰动时系统的韧性。经模拟仿真,基于该方法的排序结果如图7所示。

图7 基于文献[25]的节点结构韧性重要度排序Fig.7 Ranking of node structure resilience importance based on [25]

如果把第2.2节中的β%改为具体数值,即所有节点韧性值增加/减少相同数值Δx

(25)

图8 基于节点韧性增加/减少相同数值的节点重要性排序Fig.8 Ranking of node importance based on increasing/decreasing the same value of node resilience

对比图6～图8可知,在关键节点识别方面,本文方法和其他两种方法基本保持一致,排名前4的节点均为1,2,23,24。不过,从直观上看,后两种方法有大量节点重要性值相同,3种方法的单调性如表2所示,由表2可知本文方法具有明显的优势。

表2 单调性比较Table 2 Monotonicity comparison

(2) 肯德尔相关系数

计算公式为

(26)

式中:RT、RF分别表示一致组和非一致组的向量;n为节点数量;τ∈[-1,1],τ=1表示两个序列完全正相关,也就是说τ越接近于1,方法的精确度越高。

为分析本文方法的准确性,使节点韧性值增加相同比率(1%,2%,…,10%),考察节点重要性值变化情况,结果如图9所示。从图9可知,虽然节点重要性数值随着节点韧性增加比率值而变化,但线条没有交叉,也就是说节点重要性排序与β%的取值无关,不会发生改变,因此τ=1。这也说明本文方法相对准确、稳定。

图9 节点韧性增加不同β%情况下节点的重要性Fig.9 Node importance in case of node resilience increasing with different β%

3.2.4 本文节点重要性度量方法的应用场景分析

由式(17)可知,可通过节点韧性改变相同比率时对指挥信息系统韧性的影响程度的定量计算,来确定节点的重要性,影响程度越大,节点越重要。因此,在指挥信息系统规划设计和运行维护阶段,综合运用统计分析、作战模拟和兵棋推演等方法,获取相关数据以评估系统节点重要性,把有限的资源投入到对重要节点的韧性增强上,以增强系统韧性。

当指挥信息系统的多个节点遭受攻击时,节点恢复顺序,也就是恢复策略选择问题,将对系统韧性有较大影响。接下来考察节点重要性在恢复策略中的运用问题。假如攻方已获取守方节点拓扑关系,采取“攻心策略”,导致{1,2,3,23,24,9}等6个重要节点功能水平严重下降,现在采取不同的恢复策略进行仿真,仿真结果如图10所示。图10(a)为在某一恢复策略下,基于蒙特卡罗仿真方法的系统韧性计算,其中每条颜色不同的细曲线为单次仿真时得到的系统功能水平曲线,红色粗曲线为多次仿真得到的系统平均功能水平曲线,该红色粗曲线下方与坐标轴围成的面积与整个矩形的面积的比值即为系统韧性值。图10(b)为不同恢复策略下的系统韧性曲线,其中策略1为根据基于节点韧性增加/减少相同数值的节点重要性排序方法(图8)确定的节点重要性排序进行恢复,策略2至策略5为随机恢复策略,策略6为根据本文方法确定的节点重要性排序进行恢复。经计算,以上6种策略的韧性值分别为R1=0.887 1,R2=0.886 3,R3=0.877 5,R4=0.860 3,R5=0.886 1,R6=0.897 9。可以看出,策略6韧性值稍优于其他策略,因此该方法也可以用于恢复阶段的恢复策略制定。

图10 指挥信息系统韧性曲线与系统恢复策略关系Fig.10 Relationship between resilience curve of command information system and recovery strategy

4 结束语

本文提出了一种面向韧性的指挥信息系统节点重要性度量方法,对指挥信息系统节点重要性进行评估和排序。该方法运用指挥信息系统各个节点韧性增加/减少相同百分比时,系统韧性增加/减少程度来评估节点的重要性,能够直观地反映节点韧性与系统韧性的关系,有利于把有限的资源投入到对指挥信息系统韧性影响最为显著的节点上,以最大化增强指挥信息系统韧性。仿真实验部分验证了本文方法相比于其他方法,在单调性和肯德尔相关系数方面具有一定优势。下一步研究主要是进一步结合指挥信息系统节点的拓扑、功能等其他属性,采取多属性策略对节点重要性进行评估。