基于灰色关联协同效应权重配置的费用预测模型

赵 潞, 方志耕, 于 亮, 张亚东, 邱玺睿, 华晨晨

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106; 2. 中国航天科技集团有限公司, 北京 100048)

0 引 言

复杂装备是指客户需求复杂、产品组成复杂、产品技术复杂、制造过程复杂、项目管理复杂的一类装备,如航天器、飞机、航空母舰、武器系统等[1]。随着时代的进步,费用逐渐成为影响装备发展的首要问题,如何筛选影响复杂装备费用的关键要素并精确有效地进行费用估算预测,提高经费使用效率,越来越成为军事领域关注的重点。

现有的费用预测问题研究可分为两类,一类是通过历年的装备费用样本数据,研究仅考虑时序的费用预测问题[2-4];另一类是根据样本的费用及参数信息,对目标装备的费用进行估算预测,常见的传统方法包括参数法、类比法和工程估算法等[5]。由于影响复杂装备费用的要素众多,而装备本身又具有小样本、贫信息的特点,通过一般传统方法较难解决这类问题。王景玫等[6]针对航天装备小子样、复杂度高等问题,提出了基于技术成熟度与支持向量机的航天型号研制成本预测模型,提高了预测精度。Zhang等[7]设计了基于模糊集的民用飞机通用性指标评估方法,通过层次分析法确定各指标权重并构建神经网络模型,用于预测新型飞机的研发成本。蔡伟宁等[8]利用3种预测方法构建组合预测模型,对飞机研制费用进行预测,取得了良好效果。此外,灰色系统理论也被广泛应用于解决复杂装备小样本、多变量费用预测的问题,Jiang等[9]通过傅里叶级数的残差修正模型对传统灰色模型GM(1,N)模型进行改善,提高预测准确度。袁泉等[10]对GM(0,N)中参数的累加顺序进行改进。吴利丰等[11-12]从相似度和敏感性角度对样本数据进行重新排序,上述几种方法都提高了GM(0,N)模型的费用预测精度。Tian等[13]提出了一种基于灰色数列的IN-GM(0,N)模型,用以解决信息不确定的成本因素下商用飞机成本预测问题。Chen等[14]通过建立跨界缺失数据的特征序列N-GM(0,N)模型预测总体成本空缺数据的灰色区间,并通过对参考序列的排序将其白化,实现复杂装备总体成本的估算。Chen等[15-16]使用灰色关联分析筛选费用关键影响要素并进行相关性分析,通过二次回归分析降低要素间相关性的影响,并进行商用航空飞机的费用估算;在后续研究中,又提出了变量重要性投影分析方法和回归模型的组合,通过逐步回归解决小样本和参数间强相关性问题,以此提高成本预测精度。灰色系统理论还可以和信息熵理论[17]、神经网络[18-22]等不同理论方法结合,以进一步提高复杂装备费用预测的准确性。

随着研究的深入发现,在灰色整数阶预测结果较差时,采用分数阶模型能够取得更好的结果。文献[23-25]提出并总结了分数阶累加的离散灰色模型,并研究了其适用范围。罗佑新[26]在单变量分数阶灰色模型FGM(1,1)的基础上,建立了多变量分数阶累加灰色模型FMGM(1,N),并验证了模型的有效性。方世力[27]通过极大熵理论筛选费用关键影响要素并确定权重,构建异阶多参数分数阶灰色模型FOGM(0,N),有效提高了运载火箭费用预测精度。在已有的相关研究中,往往存在以下几个方面的问题:① 以样本数据进行建模预测时未考虑到各样本与目标间的不同相似度会对费用关键影响要素的筛选和费用预测产生影响;② 在多参数费用估算预测问题中,分数阶模型的阶数通常是一个恒等常数;③ 估算预测模型中各要素间往往存在着协同效应和共线性,难以解决这类情况下关键要素的筛选和实际权重分配问题。

本文针对同类型复杂装备小子样、贫信息的情况,根据相似信息优先原理,将各样本按与目标的相似度大小进行排序;在灰色关联度筛选并确定费用关键影响要素权重大小的基础上,提出了在要素间具有协同效应的情况下,参考Shapley值思想进行权重的进一步分配,并借助异阶参数的分数阶GM(0,N)模型进行费用预测。经过实例测算对比,本文方法能够有效地提高复杂装备费用预测的精度,证明了所提方法的有效性和可行性。

1 考虑协同效应的灰色预测模型构建

1.1 灰色关联度分析

灰色关联度分析是在小样本、贫信息下,将因素之间发展趋势的相似或相异程度,亦即“灰色关联度”,作为衡量因素间关联程度的一种方法。当两个因素变化的趋势具有一致性,即同步变化程度较高时,可谓二者关联程度较高;反之,则较低[28]。

在进行费用预测前,通过灰色关联度分析能够较为有效地确定与目标装备更为相似的样本。若样本与目标装备各参数指标值趋近一致,则二者费用应接近;若样本与目标装备各参数指标值变动趋势相似,则二者指标所对应的费用也应符合指标变动规律。同理,若多个相似样本的某一费用影响要素(即特征参数)的变动趋势与费用变动趋势一致,则说明该要素的变动引起费用的同步变动,该要素对费用的影响程度相对较大,可初步选作费用关键影响要素。灰色关联分析定义如定义1所示。

定义 1设Xi={xi(j)|i=1,2,…,n;j=1,2,…,m}为系统行为序列,X0={x0(1),x0(2),…,x0(m)}为参考序列。

则

(1)

称

(2)

为序列Xi与X0的灰色关联度[28]。

(3)

定理 1当原始数据的累加阶数r∈(0,1)时,将样本数据按关联度大小从低到高排序,与目标型号灰色关联度大的样本中,其同类要素权重更大。

x(0)(i)的系数为

x(0)(i-1)的系数为

因此,在同类要素x(r)(k)的表达式中,x(0)(i)比x(0)(i-1)具有更大的权重,x(0)(i)所在的样本对应的灰色关联度大于x(0)(i-1)所在的样本,符合相似信息优先原则,即与目标型号越相似的样本数据在建模时应具有越高的权重。

证毕

根据定理1,计算各样本型号Ai(i=1,2,…,n-1)与目标型号An费用影响要素间的灰色关联度,从低到高进行重新排序并除去关联度较低的样本数据,以保证关联度越高的样本型号数据在预测费用时所占的权重越大。最终重新排列后的数据矩阵如下所示:

(4)

此时,An-1为与所求型号An最相似的样本型号数据,A1为在满足设定的关联度边界条件下与所求型号An最不相似的样本型号数据。

对式(4)中的各费用影响要素做与费用间的灰色关联度分析,划定关联度边界值θ,当γj1(j=2,3,…,N)>θ时,保留该项要素作为费用的关键影响要素,反之则舍去,获得要素筛选矩阵如下所示:

(5)

1.2 考虑要素协同效应的Shapley值权重配置模型

一般来说,要素对费用的影响程度越大,则该要素在费用估算预测模型中的权重应越大。由于通过灰色关联度筛选的费用关键影响要素间可能存在着协同效应,若直接采用要素与费用间的灰色关联度大小来确定要素权重,则忽视了要素间协同作用的影响,使得各要素权重配置不合理,费用预测的偏差增大。通过相关性分析虽能判断两个要素间可能存在协同效应,但难以衡量单个要素对费用的实际影响程度,也难以测定各要素在费用估算预测模型中的实际权重。因此,可通过灰色比较关联重要性进行协同作用下费用关键影响要素实际权重的配置。

(6)

定义 4设γj1(j=2,3,…,m,23,24,…,23,…,m)表示各要素与费用间的灰色关联度,I={2,3,…,m}为m-1个原始要素的集合,参考Shapley值思想进行要素协同效应下灰关联提高的贡献度分配,分配计算内容如表1所示。

表1 要素灰色比较关联重要性计算表Table 1 Table for calculating importance of grey comparative association of elements

其中,s为I的子集,s⊆I;v(s)为s对应的灰色关联度,若组合后集合的灰色关联度低于组成该集合的任一原始要素的灰色关联度,则表1中该集合的v(s)=0,即该组合不存在正向协同效应;v(si)为集合s中除去要素i后剩余要素集合的灰色关联度,若v(si)>v(s),则v(s)=v(si)=0,即要素i参与后对灰色关联度提高起到负作用,加入要素i后的组合也不存在正向协同效应;v(s)-v(si)为要素i使灰色关联度提高的边际贡献;|s|为集合中元素的个数;w(|s|)为各元素个数所占的权重;w(|s|)[v(s)-v(si)]为在要素i存在协同效应的各子集中i的贡献度,累加后为要素i的总贡献度,即i的灰色比较关联重要性。

定理 2若存在要素间的灰色关联协同影响效应,集合s对应的灰色比较关联重要性权重w(|s|)=(|s|-1)!·(n-|s|)!/n!。

证毕

定理 3若存在要素间的灰色关联协同影响效应,各原始单要素的灰色比较关联重要性应为∑s∈Siw(|s|)[v(s)-v(si)],Si为子集个数。

证明s为I的子集,当s=1、即不考虑与其他要素间关系时,v(s)为该要素与费用间的灰色关联度,v(si)为除去该要素后子集中的其他要素与费用间的灰色关联度,该要素的灰色比较关联重要性权重为w(|1|)=(n-1)!/n!=1/n,故该要素在不考虑协同效应影响下的灰色比较关联重要性为w(|1|)[v(1)-v(1i)];当s=2、即考虑两个要素间的协同效应时,根据上述步骤可知,所求要素对应情况下的灰色比较关联重要性为w(|2|)[v(2)-v(2i)]。以此类推,当要素间存在灰色关联协同影响效应时,要素在各子集s下对应的灰色比较关联重要性为w(|s|)[v(s)-v(si)],故该要素的总灰色比较关联重要性为∑s∈Siw(|s|)[v(s)-v(si)]。

证毕

在构造要素灰色比较关联重要性计算表时,只考虑灰色关联度扩大的灰色关联协同影响效应,在此基础上进行相关贡献度的分配,故要素灰色比较关联重要性计算表在形式上与Shapley值计算表相似,但在不满足Shapley值思想有效性的前提下也可进行分配计算。

定理 4当存在要素间的灰色关联协同影响效应时,各关键影响要素的实际权重为灰色比较关联重要性的归一化值。

证毕

定理 5当不存在要素间的灰色关联协同影响效应时,要素的权重应为灰色关联度的归一化值。

证毕

1.3 异阶离散分数阶累加预测模型

在灰色分数阶累加模型中,多参数的累加模型阶数一般都为同阶,而异阶离散分数阶模型不同参数的阶数不同,且分别代表其权重。通过灰色关联协同效应权重配置获得各费用关键影响因子的实际权重,以此作为对应参数的累加阶数,构建异阶离散分数阶累加费用预测模型。

(7)

参数的最小二乘估计满足:

[a,b2,b3,…,bm]T=(BTB)-1BTY

(8)

其中

(9)

(10)

引理 1在异阶离散分数阶累加GM(0,N)模型中,累加阶数ri越大,在相对扰动界中影响力越大,对解的影响越敏感,反映费用影响要素的权重越大,反之亦然。相关证明过程详见文献[27]。

模型中的累加阶数ri分别为各要素在协同效应下的实际权重,由于费用不参与要素协同效应的权重分配,故其阶数r1可取各要素权重的平均值。以最小二乘求得模型系数后计算得到目标费用的r1阶累加值,通过累减还原得到预测费用。

1.4 预测模型构建及求解步骤

综上所述,基于灰色关联协同效应权重配置的费用预测模型构建及求解步骤如下。

步骤 1计算样本与待预测装备的灰色关联度。

步骤 2根据步骤1中结果的大小对样本进行筛选排序,计算各费用影响要素与费用间的灰色关联度,筛选费用关键影响要素。

步骤 3构建样本协同效应矩阵,并计算各关键影响要素协同效应下的灰色关联度。

步骤 4计算各关键影响要素的灰色比较关联重要性及权重。

步骤 5构建灰色分数阶累加预测模型并求解系数。

步骤 6将待预测装备各关键影响要素累加值代入预测模型,累减还原得到费用预测结果。

2 实例分析

2.1 民用飞机成本费用预测

为了便于比较,本文采用文献[18]中的相同样本数据进行目标装备的费用估算预测,并与原文方法进行对比,以此证明本文方法的合理性及可行性。

表2为部分进行脱密处理后的民用飞机参数和成本费用信息,现使用表中前7组数据,对机型8和机型9两种大型飞机的成本费用进行预测,并对预测结果精度进行比较。

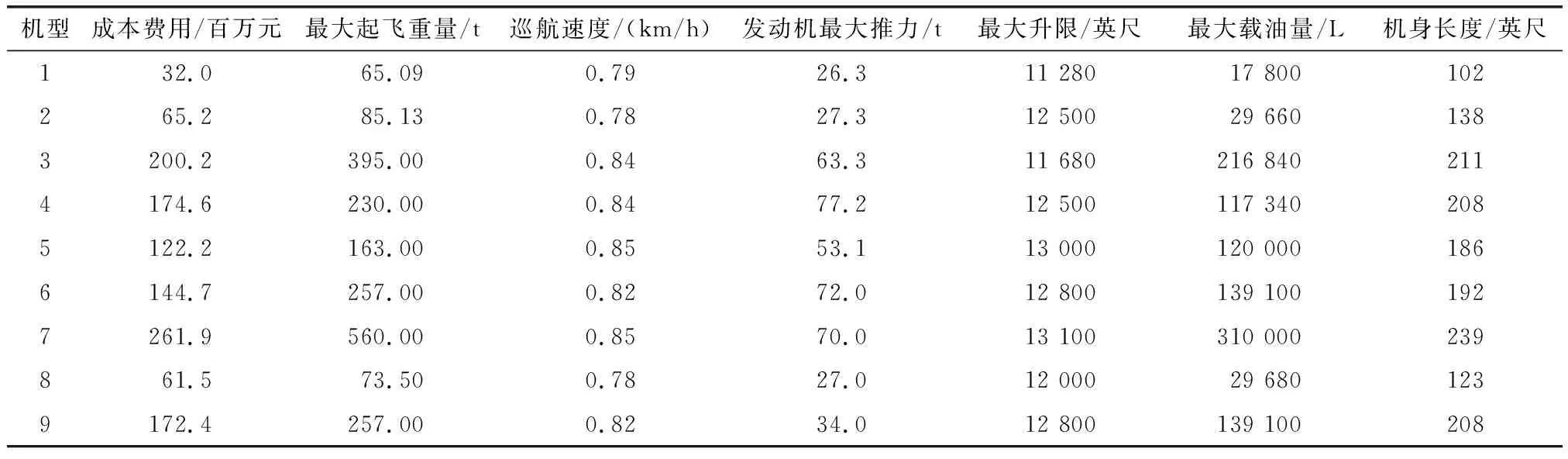
表2 各型号民用飞机成本费用与相关参数Table 2 Cost expenditure and related parameters of each type of civil aircraft

步骤 1原始数据无量纲化处理。

以机型8为待预测装备为例,通过均值法进行无量纲化处理,消除数据中不同量纲的影响,得到处理后的数据矩阵如表3所示。

表3 各型号民用飞机成本费用与相关参数处理表Table 3 Cost expenditure and related parameter processing table of different types of civil aircraft

步骤 2计算各样本与待预测型号的灰色关联度。

由于机型8为待预测装备,没有成本费用数据,在计算样本与待预测型号的灰色关联度时仅考虑各费用影响要素间的相似性。根据式(1)和式(2)计算样本型号1～7与待预测型号8的灰色关联度,此时系统行为序列为

以此类推,分别计算得到各样本与待预测型号的灰色关联度并划定边界值θ,将关联度大于θ的样本型号按关联度从低到高进行排序,此处取θ=0.60,计算结果如表4所示。

表4 型号8灰色关联度排序表Table 4 Model 8 grey relational grade ranking table

步骤 3筛选费用关键影响要素。

对筛选完成后不包含待预测装备的数据矩阵重新进行无量纲化处理,以便根据高相似度的样本数据进行费用关键影响要素的选取。筛选排序并无量纲化后的数据矩阵如表5所示。

表5 筛选排序数据处理表Table 5 Filtering and sorting data processing table

对表5中的费用影响要素,即特征参数进行筛选,确定关键影响要素,此时系统行为序列为各费用影响要素序列:X1={2.233 3,1.575 3,1.024 9,0.917 3,0.650 1,0.259 6,0.339 5},X2={1.031 2,1.019 1,0.994 8,1.019 1,1.031 2,0.958 4,0.946 3},…,X6={1.311 1,1.157 5,1.053 3,1.141 1,1.020 4,0.559 6,0.757 1};参考序列为X0={1.831 8,1.400 3,1.012 1,1.221 2,0.854 7,0.223 8,0.456 0}。

根据式(1)和式(2)计算得到上述民用飞机的费用影响要素与费用间的灰色关联度分别为:0.748 5,0.583 5,0.683 2,0.570 4,0.737 7,0.679 7。由式(9)和式(10)可知,第1行的样本数据一般不参与分数阶累加预测模型的系数求解,而在测算过程中往往取比参与计算的样本数量少2个左右的要素作为费用关键影响要素[27]。当选择要素过多时,不易求解含常数项的分数阶累加预测方程系数;当选择要素过少时,所建立的方程丢失信息过多,忽略了部分对费用变动较为敏感的要素。由于灰色关联度越高,要素对费用的影响程度越大,此处设定影响要素灰色关联度边界值θ=0.65,故选取最大起飞重量、发动机最大推力、最大载油量和机身长度作为民用飞机费用的关键影响要素。

步骤 4构建协同效应矩阵并计算要素灰色关联度。

将费用关键影响要素指标值分别相乘,构建如式(6)所示的协同效应数据矩阵,对所得矩阵进行无量纲化处理后根据式(1)和式(2)分别计算单要素指标、两要素相乘指标、三要素相乘指标、…、n要素相乘指标与费用间的灰色关联度,以判断是否存在协同效应,计算结果如表6所示。

表6 协同效应下要素与费用的灰色关联度Table 6 Grey relational grade between elements and costs under synergistic effect

步骤 5要素间协同效应下权重的分配。

根据定义4,通过Shapley值思想计算各要素的灰色比较关联重要性,具体过程如表7所示。

表7 要素1灰色比较关联重要性计算表Table 7 Table for calculating relational importance of grey comparative of elements 1

根据定理3,由表7中数据计算结果可知,要素1的灰色比较关联重要性为

φ1=0.173 8+0.014 3+0+0.017 3+0+0+0+

0=0.205 4。

同理可得φ2=0.182 5,φ3=0.204 2,φ4=0.224 5。由此,可根据定理4确定各要素对费用影响程度的权重为w1=0.251 6,w2=0.223 5,w3=0.250 0,w4=0.274 9。

步骤 6灰色分数阶累加预测模型构建及求解。

根据引理1,以步骤4中获得的各要素权重作为分数阶累加预测模型中各要素的累加阶数,由于费用不参与要素协同效应的权重分配,故费用项的阶数为各要素权重的平均值0.25。根据分数阶累加公式:

以此分别计算各费用关键影响要素的样本参数累加值,得到样本数据矩阵为

Y=(265.675,235.671 9,272.747 7,236.857 1,
147.046 5,161.281 7)T

通过式(8)最小二乘法求得分数阶累加预测模型的系数值,将其代入式(7),得到分数阶累加预测模型为

步骤 7累减还原得到预测结果。

由于该预测模型所需的自变量值为分数阶累加后的参数值,因此在进行费用预测时需通过分数阶累加公式计算在已有样本情况下待预测型号的各参数累加值,即

累减还原后得到型号8的预测费用为

预测误差为-9.561 6%。经过相同步骤得到型号9的预测费用为172.933 8百万元,预测误差为0.309 6%。与原文模型的拟合预测对比结果如表8和表9所示。

表8 多元线性回归模型、GM(0,N)模型、GM(0,N)-BP组合模型与本文模型拟合预测效果检验表Table 8 Multiple linear regression model, GM(0,N) model, GM(0,N)-BP combination model and the proposed model fit prediction effect test table

表9 不同预测模型平均误差结果对比Table 9 Comparison of the average error results of different prediction models %

由表8和表9可知多元线性回归、GM(0,N)模型和GM(0,N)-反向传播(back propagation, BP)神经网络组合模型的平均拟合误差分别为1.980 0%、5.325 7%和0.002 9%,预测平均误差分别为16.670 0%、26.725 0%和11.650 0%。与这3种方法相比,采用本文所提方法的拟合误差为1.562 9%,预测平均误差降低到4.935 6%,拟合精度相比前两种方法均有所降低,而预测平均误差为所采用的4种方法中最佳的。

为避免数据测算出现的偶然性,证明本文所提出的方法具有一定的有效性和可行性,对表2中各型号的费用分别进行了估算预测,预测结果如表10所示。

表10 各型号民用飞机成本费用预测误差表Table 10 Cost expenditure forecast error of each type of civil aircraft

表10中的预测结果表明,通过本文方法对多组参数样本分别进行模型构建和费用预测,尽管由于部分待预测型号与其余已知样本间的总体灰色关联度不高,相似程度较低,使得预测误差相对较大,但预测结果的平均误差为6.41%。若使用与目标更为相似的多个样本则能使预测精度进一步提高,总体而言,预测结果仍具有较高的精确性,在一定程度上能够满足工程实际问题中的需要。

2.2 原样本变化情况下民用飞机成本费用预测

由于在样本相似度排序和费用关键影响要素筛选中都运用了灰色关联分析,当样本数量变动时,有时会导致排序顺序和要素筛选结果的变动,从而使得预测模型及预测结果发生变化。本节以表2中的数据为例,分别考虑新增和减少一个民机样本的情况下,型号8的成本费用预测变动情况。

(1) 减少一个样本数据

去除表2中与型号8灰色关联度较高的样本型号1,计算得到剩余样本与待预测型号的灰色关联度如表11所示。经上述步骤计算得到各费用影响要素与费用间的灰色关联度分别为:0.661 7,0.563 6,0.616 9,0.531 1,0.689 2,0.653 7。

表11 型号8灰色关联度排序表Table 11 Model 8 grey relational grade ranking table

当选择最大起飞重量、发动机最大推力、最大载油量和机身长度4个要素作为费用关键影响要素时,各要素的累加阶数(即权重)分别为0.228 7,0.261 4,0.244 7,0.265 2,费用的累加阶数为0.25。通过最小二乘回归得到型号8的费用估算预测模型为

经预测得到型号8的费用为44.41百万元。

当选择最大起飞重量、最大载油量和机身长度3个要素作为费用关键影响要素时,各要素的累加阶数(即权重)分别为0.335 3,0.285 1,0.379 6,费用的累加阶数为1/3。通过最小二乘回归得到的型号8的费用估算预测模型为

预测所得型号8的费用为48.654 8百万元。

(2) 增加一个样本数据

在表2样本数据的基础上,增加型号10的样本数据,其费用及各参数值如表12所示。计算得到的所有样本与待预测型号8的灰色关联度如表13所示。

表12 型号10样本数据Table 12 Model 10’s sample data

表13 型号8灰色关联度排序表Table 13 Model 8 grey relational grade ranking table

经上述步骤计算得到各费用影响要素与费用间的灰色关联度分别为:0.715 8,0.542 7,0.812 1,0.540 3,0.640 5,0.657 1。设定灰色关联度边界值θ=0.60,选择最大起飞重量、发动机最大推力、最大载油量和机身长度4个要素作为费用关键影响要素,各要素的累加阶数(即权重)分别为0.226 8,0.321 2,0.200 7,0.251 4,费用的累加阶数为0.25。通过最小二乘回归得到的型号8的费用估算预测模型为

预测所得型号8的费用为57.36百万元。

与原样本数据预测对比的结果如表14所示。

表14 不同样本量预测结果及误差对比Table 14 Comparison of prediction results and errors for different sample sizes

通过预测结果对比分析可知,由于本文预测模型中相似样本的选取排序、关键影响要素的筛选和权重的设定都是基于灰色关联度进行的,当样本数量发生变动时,各样本间及要素与费用间的灰色关联度都会发生变动,导致最终预测结果发生改变。通过对比原始数据和增减样本后的要素灰色关联度可以发现,在减少一个相似度较高的样本后,剩余样本的总体灰色关联度降低,预测结果偏差增大;在增加一个相似度较高的样本后,样本的总体灰色关联度提高,预测结果偏差变小,且在样本变动时,各要素灰色关联度间的大小关系发生了变化,由此可见样本量的变动会对关键影响要素的筛选产生影响。因此,在原有样本数据发生变动时,关键影响要素的选取、权重的确定和预测模型也会发生相应的改变,预测结果也会发生变化。

此外,通过算例对比分析可知,在小子样情况下,关键影响要素选择比样本数量少2时能够在一定程度上提高预测精度;样本与待预测装备的总体灰色关联度越高,关键影响要素的筛选及权重的确定越准确,预测精度越高。

3 结束语

本文提出了一种基于灰色关联协同效应贡献度分配的由要素权重配置确定灰色多元离散分数阶模型阶数的方法。该方法考虑了各费用影响要素间的协同效应,依据各要素灰色比较关联重要性的大小,将权重分配到各个独立要素中,进一步挖掘了费用影响要素的潜在作用。预测结果显示,该方法比传统的多元线性回归、GM(0,N)模型及部分改进后的GM(0,N)模型具备更高的估算预测精度,也具有一定的适用性。

在复杂装备研制初期,尤其是样本量不足、相关的费用影响要素较少且存在大量协同效应的情况下,本文提出的方法能够更好地适用于复杂装备的费用估算,并取得了良好的预测效果。

本文通过灰色关联协同效应权重配置模型和异阶灰色分数阶累加预测模型,较好地解决了贫信息背景下同类或相似类型复杂装备的费用预测问题,但在面对全新的新型复杂装备费用预测问题时,可能出现以往样本与待预测新装备关联度低或无样本信息的情况。本文方法仅能通过添加与目标装备的费用关键影响要素较为接近的样本来尝试进行预测,易出现预测偏差较大或无法进行预测的结果。因此,在面对全新的复杂装备时,如何对费用进行精准预测,仍需进一步研究。