基于改进灰狼算法的舰载机弹药保障调度优化

刘 哲, 马俊飞, 陈佳峰, 马嵩华,*

(1. 山东大学机械工程学院, 山东 济南 250061; 2. 高效洁净机械制造教育部重点实验室,山东 济南 250061; 3. 山东大学机械工程国家级实验教学示范中心, 山东 济南 250061; 4. 湖南云箭集团有限公司, 湖南 长沙 419503)

0 引 言

航空母舰是世界上各军事强国最重要的海上战略支撑平台,其主要的作战方式是调度起降舰载战斗机进行对空、对海作战,因此航空母舰编队作战对舰载机弹药的供应有很高的要求[1]。在供应过程中,需要弹药升降机、弹药装配舱以及弹药运输车等保障设备紧密配合,完成弹药清点、补充、装配、转运等复杂工作[2]。其中,耗时最长、涉及人员和设备最多、贯穿于服务保障全程的是航空弹药转运流程,其效率直接决定着舰载机的出动架次以及作战能力[3]。因此,亟需一种有效的调度优化方法来提高弹药转运流程的作战保障效率。

在目前日益紧张的国际局势下,进一步提高海上作战能力也成为各国重要的发展任务,对于航空母舰舰载机弹药保障调度流程的研究得到了国内外学者更多的关注。Smith[4]分析了弹药存储仓库在快速响应多个需求任务时存在的检索困难问题,将存储作战载荷检索过程建模为并行机动调度问题,并利用综合需求进行仿真。Yu等[5]建立了弹药保障及时条件下的航空保障群预调度模型和保障不足时的全反应调度模型,并设计了仿真实验验证模型的可行性与有效性。Yuan等[6]提出需要在原有的调度任务事先设计规划方式的基础上增加动态飞行甲板环境下的舰载机保障与调度方法,对调度过程中出现的意外中断实时做出更优的决策,以根据作战态势的实时动态性获得更可靠的舰载机弹药保障与调度指导。Ryan等[7]开发了一个航空母舰飞行甲板操作决策支持系统,该系统在操作人员为飞行甲板资源保障调度流程设置相应目标和约束后,会通过计算返回建议的时间表,供操作人员参考。Feng等[8]考虑到调度过程中资源冲突的显著影响,设计了一种基于改进蚁群优化算法的寻优调度策略,有效解决了路径规划与资源分配问题。Su等[9]分析了舰载机群出动保障流程的出动时限、保障人员、保障设备等诸多约束,建立了混合整数规划模型,并通过典型算例完成了模型验证。Liu等[10]提出了一种改进的可变邻域搜索算法,用于解决航空母舰甲板固定资源站配置与航空母舰舰载机飞行前准备调度的联合优化问题。吕晓峰等[11]针对模块化弹药调度问题,建立了舰载机模块化弹药调度模型,并使用改进的遗传算法对模型进行了求解。

舰载机弹药保障这一优化调度问题,经历了人工经验调度、计算机辅助调度、智能决策和优化调度3个发展阶段[12],目前主要通过智能优化算法和虚拟仿真求解。公开的研究表明[13],人类操作员与智能优化决策系统之间的约束设定、选择接受等高级交互可以实现整体任务性能的显著提升。Liu等[14]针对航空母舰飞行甲板航空保障资源站受限于固定位置的问题,提出了一种改进的具有4种原始邻域结构的可变邻域搜索算法。经验证,该算法可以有效求解航空保障资源站保障供应问题。飞行甲板上的弹药保障调度流程可以抽象类比为一类柔性流水车间调度问题[2],由于这类问题在港口货运调度、柔性车间生产线、轨道运输调度等场景中已有成熟应用[15],迁移解决飞行甲板弹药保障调度仍有较大实用价值。Wang等[16]总结对比了舰载机调度保障路径规划的典型技术与算法,并讨论了相应的跟踪控制技术,结合现有技术问题提出了路径规划问题的重点改进方向。Yu等[17]利用整数线性规划公式提出一种有起飞优先级的飞行甲板调度问题,并通过设计一种改进的差分进化算法获得了较好的调度方案。Ye等[18]将基于案例的推理方法与最邻近法和层次分析法结合,提出了一种有效挖掘历史数据的应用方法,为弹药保障预测性供应提供了指导。

本文针对航空弹药在航空母舰飞行甲板上转运过程中的保障调度流程及约束,设计了一种改进的灰狼优化(grey wolf optimizer,GWO)算法。在传统GWO算法的基础上,本文改进编码解码策略,使用整数编码方法,并通过将负整数作为分组标记实现整数解向量的多目标分组。在GWO算法跟随头狼狩猎靠近的基础上,改进GWO算法也增加了灰狼个体自由搜索策略以避免算法求解陷入局部最优的问题,保证实时有效的调度优化决策。

1 问题描述

航空弹药通过弹药升降机转运至航空母舰飞行甲板后,需要由弹药运输车依次将弹药运输到各舰载机停机区域暂存,再按照舰载机出动顺序依次完成弹药挂载工作,主要场景如图1所示。

图1 航空母舰飞行甲板弹药运输场景Fig.1 Flight deck ammunition transport scenario of aircraft carrier

在弹药在航空母舰飞行甲板上转运过程中,建立如下问题模型。

现场有P个弹药升降机供应航空弹药;N辆装载容量为Q的弹药运输车,运输车具备弹药运输和装载的功能。弹药从弹药升降机出发,向K个目标工作点运输并装载弹药,包括k个运输暂存目标工作点和K-k个弹药装载目标工作点。各运输车初始位置可根据整个路径各目标工作点等待时间最短的要求,在P个弹药升降机中进行选择[19]。考虑现场环境复杂多变,补充设计影响运输过程的相关因素集合U,包括升降机仓储余量、运输车工作能力、运输人员素质、现场环境等参数。同时,要求较高的目标工作点设置严格的工作时间窗[sti,fti]。各目标工作点的等待时间是运输车到达该目标工作点前走过的路程所需的时间。同一运输车可能经过多个目标工作点,因此同一路径上的各目标工作点等待时间具有累加的特性。考虑实际作战情况对保障时间要求极为严格,故本问题以满足优先运输条件、最短等待时间为目标,设计以目标工作点为中心的保障调度策略。

所建立问题模型的解应为不多于N条的哈密顿回路,应确保这些哈密顿回路经过了所有目标工作点,且所有目标工作点的等待时间总和最少。如果一辆运输车的路径同时包含了运输暂存目标工作点和装载目标工作点,则必须保证运输车到达运输暂存目标工作点的顺序早于装载目标工作点,即运输车在执行装载任务前确保全部弹药已运输卸载完毕,同时确保运输车在路径上所有运输暂存目标工作点的总需求量不超过其装载容量。

在弹药装载调度保障现场场景中,在任务、资源、环境等情况不确定的情况下,问题存在的难点较多,处理起来比较复杂。为简化和说明问题,特做如下合理假设[20]:

(1) 弹药、运输车沿既定路径单向运输,即弹药只能从弹药升降机运往各目标工作点,不会重复经过同一路径;

(2) 运输车装载容量有所限制,且容量大于任一个目标工作点的需求量;

(3) 各运输车在运输过程中,在无人为干扰的情况下始终以最大转运速度工作;

(4) 各运输车均从升降机处出发,完成工作后返回出发升降机位置,即各运输车路径的起点、终点都是升降机,运输路径构成一条哈密顿回路;

(5) 弹药升降机、各目标工作点位置确定,且各工作点内容(弹药数量、工作时间、搬运路线)确定;

(6) 运输车为多功能车,可分别完成运输和装载任务;

(7)运输车等设备的故障时间和修复时间均服从相互独立的指数分布。

将本文出现的弹药飞行甲板保障调度流程相关参数变量列举为参数变量表,如表1所示。

表1 转运调度流程相关参数变量表Table 1 Variable table of transfer scheduling process related parameters

2 模型建立

2.1 模型定义

在弹药调度转运过程中,任一装载目标工作点完成补充、装载任务即进入战斗待命状态,因此针对运输调度过程中同一路径上多目标工作点应分别单独计算等待时间,将同一批次全部目标工作点进入战斗待命状态后的等待时间之和应评价对问题模型求解的优劣。

在默认状态下,运输车以最大速度运行,即运输车在升降机、目标工作点之间完成转运任务时花费的时间与路径路程为正比关系。设运输车n到达目标工作点i的路径有向集合为W,则各目标工作点的等待时间如下所示:

(1)

其中,

考虑式(1)中计算路径路程采用的是相邻两目标工作点间的直线距离,且无法保证两点连线与飞行甲板上其他设备、装置等不发生干涉。因此,补充中间目标工作点集合WM,将两点之间的直线距离通过添加至少一个中间目标工作点转化为若干段直线距离,以避开原定两点连线经过的障碍物,如图2所示。对所有路径目标工作点组合逐一检查并将各中间目标工作点按照初始首尾目标工作点索引方式添加至中间目标工作点集合WM。

图2 中间目标工作点距离计算Fig.2 Calculation for middle target working point distance

在复杂的作战环境中,可能会在特定时间段有执行紧急作战任务的舰载机。因此,设置部分有较高权重的目标工作点,针对任务紧急程度设置严格的工作时间窗,即

(2)

式中:P(tin)是违反时间窗口要求的惩罚成本;atin是未开始接受工作支持的最早临界时间点;btin是停止接收工作支持的最晚临界时间点;r1和r2是相应情况下惩罚成本的单位费用。

为方便分析求解算法针对问题模型求解的优劣性,设置解的适应度值F与总体等待时间t成反比,即

(3)

式中:M为一个较大的常数。适应度值越大,表示这一组通过求解算法获得的解越优质,适应度值收敛即反映求解过程获得最优解。

综合上述求解方案,本文针对问题模型优化求解的目标是在保证满足特定时间要求的任务完成的情况下,尽可能地获得最短的总体等待时间T,或获得最优的适应度值Ff,即

(4)

2.2 模型约束

在航空弹药转运最优任务目标完成的同时,仍需满足以下约束条件。

(1) 问题模型中所有的目标工作点必定有一辆运输车经过,且只会经过一次,即有

(5)

(2) 各运输车对应一个哈密顿回路,不会出现多于N的路径数量,即

(6)

(7)

(3) 各运输车运载弹药量不超过其容纳弹药的上限,即

(8)

(4) 各运输车的出发位置根据路径首个目标工作点的位置确定:首个目标工作点与各升降机距离Lia,Lib,…,Lim,选择距离最小的升降机作为起点。

L=min{Lia,Lib,…,Lim}

(9)

3 改进的离散GWO算法

GWO[21]算法是通过模拟狼群狩猎时普通灰狼在头狼的指引下不断靠近猎物的机制来获得最优解的一种启发式算法。其在解决作业车间调度问题等组合优化问题上有出色效果[22-24]。传统的GWO算法采用实数编码且多针对单目标问题,难以解决多目标排列次序问题[25]。因此,本文通过对GWO算法进行改进以求解上述问题模型。本文采用的改进GWO算法使用整数编码方法,并通过将负整数作为分组标记实现整数解向量的多目标分组。在GWO算法跟随头狼狩猎靠近的基础上,改进的GWO算法也增加了灰狼个体自由搜索策略,以避免算法求解陷入局部最优的问题。

上述调度问题模型是典型的组合优化问题,既要确定各运输车的行驶路径(即确定目标工作点的排列次序),又要将目标工作点分配给不同的运输车,即确定目标工作点的分组。

3.1 问题编码

本文采用离散化的整数编码,对各目标工作点由1至K依次以连续整数进行编号区分,同时对各运输车由-N至-1以连续负整数进行编号区分。每一个解向量中都包含对应目标工作点数K的范围从1到K的正整数,且保证各数都出现且仅出现一次;同时,包含对应运输车数量N的从-N到-1间的负整数,各数同样出现且仅出现一次。如此,N+K个整数在各个解向量中的排列顺序就对应了一组完成编码的解。

3.2 解码思路

在解向量中的正整数对应的实际调度中,编号对应该整数值的目标工作点,其N个目标工作点被负整数分隔为N组,其中-1数值固定为每一解向量的首位。在两个负整数之间或最后一个负整数之后,一组正整数序列作为其前面一个负数对应标号的运输车的工作路径。即对应负数编号的运输车从弹药升降机出发,按照正整数序列顺序到达相应标号目标工作点完成工作任务,最后再回到弹药升降机。

3.3 运输车起点、终点选择

确定了运输路径的一辆运输车在选取起点和终点时采用虚拟车场解决多车场问题,假设P个升降机均与增加的一个虚拟升降机有一条路径连通,且路径长度均为0,即设定所有运输车均由虚拟升降机处出发,具体通过哪一个实际升降机位置则由其路径上目标工作点的位置决定。距离路径上第一个目标工作点最近的升降机作为这一运输车从虚拟升降机出发经过的第一点,距离路径上最后一个目标工作点最近的升降机作为回到虚拟升降机经过的最后一点。

3.4 改进GWO算法的应用

GWO算法在求解此类调度问题中有收敛速度快、精度可靠等突出优点。传统的GWO算法随机生成初始解,易导致收敛速度慢,且缺少跳出局部最优的必要过程,因此需要对传统GWO算法进行改进。改进后的GWO算法流程如图3所示。

图3 改进后的GWO算法流程图Fig.3 Flowchart of improved GWO algorithm

GWO算法相较于经典的遗传算法对于初始解的优化程度要求较高,因此本文改进的GWO算法在生成随机初始灰狼种群后对种群适应度较差的劣势个体进行了淘汰;同时,按照轮盘赌的方式选取适应度相对较优的个体相互交叉,获得新的个体用于补充淘汰劣势个体后种群的空缺位置[26],如图4所示。其中,片段长度在解向量长度1/3～2/3范围内通过随机向下取整获得,交叉点位根据片段长度在合理范围内通过随机数确定。

图4 劣势个体淘汰后的交叉补充Fig.4 Cross-supplementation after elimination of disadvantaged individuals

种群中每个个体更新位置要向头狼移动,即按照一定的比例向其中一只头狼靠近。靠近方法为利用适应度差值决定移动距离,如下所示:

(10)

式中:φ表示在区间[0,1]的随机浮点数;Ψ1和Ψ2表示选择概率常数,依此来确定每一灰狼个体所选择跟随的头狼概率;li表示灰狼个体向选定头狼移动的片段长度;lXl表示解向量的总长度;γ为片段选择系数。

狩猎靠近过程表现为在头狼个体路径解中复制相应长度的片段,根据所得长度随机确定有效的插入点,完成插入后对重复、缺少的数据进行筛选、裁剪和补充[27],如图5所示。在局部范围搜索则为单一个体进行自我改进,完成个体内的一定片段的互换、抽取和插入操作,且在完成局部搜索后同样对重复、缺少的数据进行筛选、裁剪和补充,如图6所示。

图5 狩猎靠近过程Fig.5 Hunting approach process

图6 局部搜索过程Fig.6 Local search process

4 算法验证

以问题模型中包括3个弹药升降机、5辆装载容量为2的弹药运输车为例,假设向16个目标工作点完成运输和装载任务[28],其中包括运输暂存目标工作点和弹药装载目标工作点各8个,各点位的相关信息如表2所示。在Unity软件内置的C#脚本中编写并运行上述改进GWO算法,并与传统遗传算法对相同问题模型的处理结果进行对比[29],其适应度随迭代次数的变化情况如图7所示。独立重复使用上述两种算法分别对问题模型求解20次[30],对比结果如表3所示。获得的最优调度解及其调度路线方案如图8所示。

表2 各目标工作点位信息表(3个升降机加16个目标工作点)Table 2 Information table for each site (with 3 lifts and 16 target working sites)

表3 算法优化结果对比(3个升降机加16个目标工作点)Table 3 Comparison of algorithm optimization results (with 3 lifts and 16 target working sites)

图7 算法适应度值随迭代次数变化情况(16个目标工作点)Fig.7 Variation of algorithm fitness values with iterations number (with 3 lifts and 16 target working sites)

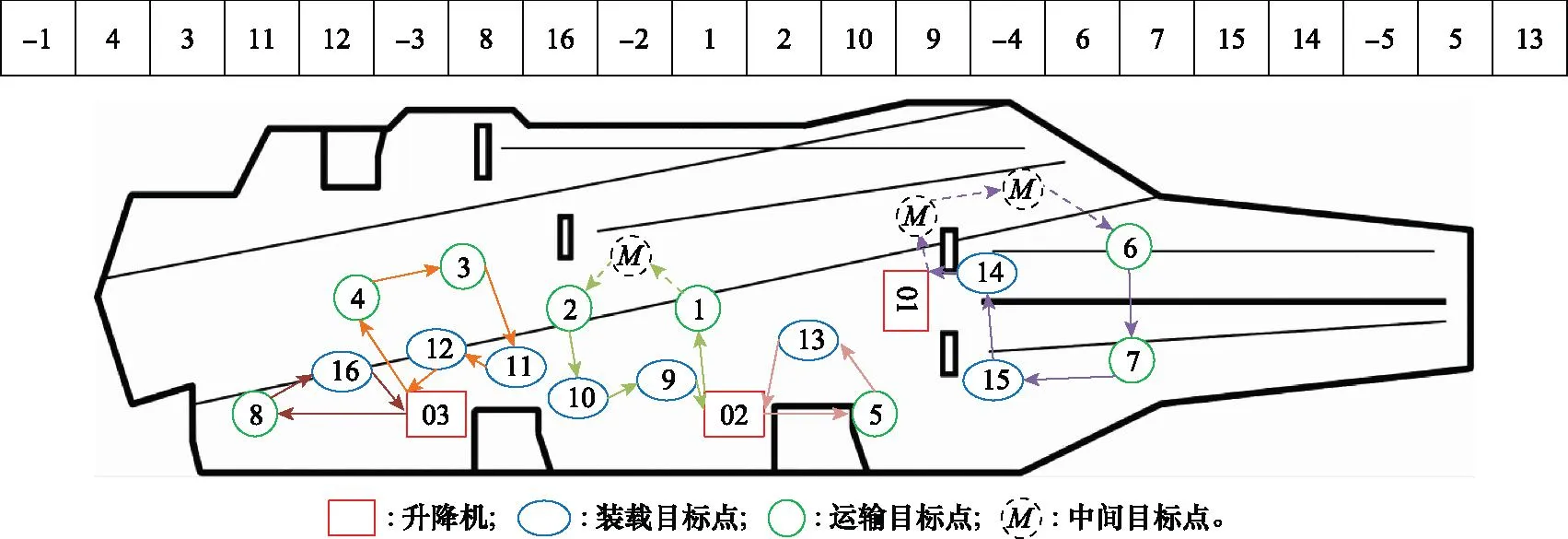
图8 最优调度解及其调度路线方案(16个目标工作点)Fig.8 Optimal scheduling solution and its scheduling route scheme (with 16 target working sites)

为进一步验证算法对更大规模问题模型的优化求解能力,修改问题模型包括3个弹药升降机和8辆装载容量为2的弹药运输车,向24个目标工作点完成运输和装载任务,其中包括运输暂存目标工作点和弹药装载目标工作点各12个,各点位的相关信息如表4所示。采用改进GWO算法与传统遗传算法处理结果对比的方式,获得的适应度随迭代次数的变化情况如图9所示,20组独立重复实验获得的对比结果如表5所示,获得的最优调度解及其调度路线方案如图10所示。

表4 各目标工作点位信息表(3个升降机加24个目标工作点)Table 4 Information table for each target working site (with 3 lifts and 24 target working sites)

表5 算法优化结果对比(3个升降机加24个目标工作点)Table 5 Comparison of algorithm optimization results (with 3 lifts and 24 target work sites)

图9 算法适应度值随迭代次数的变化情况(24个目标工作点)Fig.9 Variation of algorithm fitness values with iterations number (with 24 target worksites)

图10 最优调度解及其调度路线方案(24个目标工作点)Fig.10 Optimal scheduling solution and its scheduling route scheme (24 target working sites)

由上述结果能够直观地看到,本算法对此类运输调度问题的求解十分有效。经多次实验对比,本文获得的问题解较遗传算法收敛结果更优,且收敛速度更快。多主体虚拟仿真系统实验证明,所得到的解在大多数情况下是理论情况下的最优路径解[31],证实所提算法求解精度也十分可靠。

5 结束语

在影响现代战争的诸多因素中,保障是一项高度基础和重要的环节,改进航母飞行甲板上舰载机弹药调度保障效率有十分重要的战略意义。为保障舰载机弹药调度更高效、更可靠地完成,本文通过补充直线转运路径中间点定义、整数编码、负整数标志分组等方法设计了改进GWO算法。通过问题模型实例验证,本系统能高效地完成调度方案规划,相比传统优化算法具备更优秀的效率和精度,对大型作战场景的优化调度保障有较好的指导意义,未来通过进一步的改进完善定会在高频次作战保障上发挥重要作用。