基于RMDLPP的雷达空中目标分类

刘帅康, 曹 伟, 管志强, 杨学岭,2, 许金鑫

(1. 中国船舶集团有限公司第七二四研究所, 江苏 南京 211153; 2. 南京航空航天大学电子信息工程学院, 江苏 南京 211106)

0 引 言

雷达自动目标识别技术(radar automatic target recognition, RATR)是指利用雷达发射电磁波照射目标, 对获得的回波进行分析以确定目标的种类、 型号属性的技术[1]。随着空中目标飞机性能的不断提升,回波的调制逐步趋于多样化,国家空防安全面临的挑战也日趋严峻。研究防空系统如何能实时高效的识别空中目标,对国家空防安全具有重大的现实意义。

目前,对窄带雷达目标的识别主要有人工提取特征和自动提取特征两种。人工提取特征主要从振幅偏差系数、时域波形熵、频域波形熵、调制带宽和二阶中心矩等[2-6]特征进行提取,然后对目标进行分类,这种方法可以得到较高的识别率,但严重依赖于专家知识,一定程度上限制了适用范围。自动提取特征一般为神经网络提取特征,常见的有卷积神经网络(convolutional neural network, CNN)[7-11]、生成对抗网络(generative adversarial network, GAN)[12]和双向长短时记忆(bidirectional long short-term memory, Bi-LSTM)网络[13-14]以及这些网络的变形。神经网络方法对数据量较多时能取得较好的效果,但对于数据量少且复杂多变的调制信号往往效果不佳。

特征降维作为自动提取特征的方法可以很好地解决数据量少分类效果不佳的问题。特征降维方法包括线性降维方法和非线性降维方法。常用的线性降维方法包括主成分分析(principal component analysis, PCA)[15]和线性判别分析(linear discriminant analysis, LDA)[16]。线性降维算法在雷达目标识别中也有一些应用[17-19],全大英等人[17]将时频图中提取到的特征通过PCA进行降维,并将降维后的特征参数送入支持向量机(support vector machine, SVM)中进行识别,得到了较高的准确率。然而,由于调制数据在空间中的分布具有非线性结构,线性降维算法无法满足降维需求。常用的非线性降维算法包括等距离映射(isometric mapping, ISOMAP)[20]、局部线性嵌入(locally linear embedding, LLE)[21]等。之后对非线性降维算法的改进主要围绕局部性进行,其中最具代表性的为局部保持投影(locality preserving projection, LPP)[22-23]。为了能更好地利用标签信息, 鉴别局部保持投影(discriminant locality preserving projections, DLPP)[24]作为改进算法被广泛使用,然而DLPP在样本数据量小于样本维度数时会出现类内离散度矩阵奇异的问题。

为解决类内离散度矩阵奇异问题,目前主流的有4种方法:① 先通过PCA降维至样本维度小于样本数据量,再通过LPP降维,这样可以避免LPP降维时出现的内离散度矩阵奇异问题;② 通过指数DLPP(exponential DLPP, EDLPP),将类间离散度和类内离散度指数化后再进行运算,从而消除矩阵奇异的问题[25-26];③ 通过合成少数过采样DLPP(synthetic minority oversampling technique DLPP, SMOTE-DLPP),在进行DLPP运算前先使用过采样技术对数据进行扩充,样本数据量大于维度时,便不存在矩阵奇异问题[27];④ 通过最大差分准则局部保持投影(locality preserving projection maximum difference criterion, LPPMDC),将LPP与最大差分准则(maximum difference criterion, MDC)相结合,通过矩阵变换和矩阵指数的近似替换可以将LPP方法近似为一个简单的标准特征值问题,从而避免了类内离散度矩阵奇异的问题[28-29]。通过以上解决方案,可以很好地解决类内离散度矩阵奇异的问题。然而,对于调制数据中出现的孤立点和可分性差的问题仍需要解决。研究发现,将两样本点的欧氏距离和样本均值相关联能很好地解决孤立点鲁棒性差的问题[30],且使用Fisher判别分析可以增加高维特征样本的可分离性[31]。

针对以上思路,本文提出了鲁棒性边界DLPP(robust margin DLPP, RMDLPP)用于窄带雷达空中目标分类。首先,计算样本之间距离时将两样本点的欧氏距离与同类样本均值相关联,增强算法对孤立点的鲁棒性;其次,挑选一定数量的边界样本点进行处理并对优化DLPP目标函数进行降维,即克服DLPP存在的类内离散度矩阵奇异问题又增加类别间的区分度;最后,使用高性能的分类器对降维后的数据进行分类。通过对X波段对空警戒雷达实测数据对比实验验证了该方法的有效性。

1 相关算法

1.1 DLPP

DLPP是在LPP和Fisher判别分析两种方法的基础上发展而来的有监督学习算法,其目标函数为

(1)

(2)

Bij为第i类和第j类之间的权重,定义为

(3)

式中:σ为调节系数。

DLPP目的是使目标函数最小化,从而求得最优投影矩阵W。

1.2 边界Fisher分析

边界Fisher分析利用样本的局部关系构建权重矩阵,算法采用本征图G+={G,V+}来描述同类样本之间的紧密性,用惩罚图G-={G,V-}来描述类间可分性,具体定义如下:

(4)

(5)

边界Fisher分析的优化目标函数为

(6)

式中:X为输入样本;D为对角矩阵,定义为

(7)

边界Fisher分析目的是使目标函数最大化,从而求得最优投影矩阵W。

1.3 集成学习分类器

集成学习分类器是将若干个弱分类器组合之后产生一个新的强分类器,本文采用的是Bagging方法,Bagging方法概要图如图1所示。

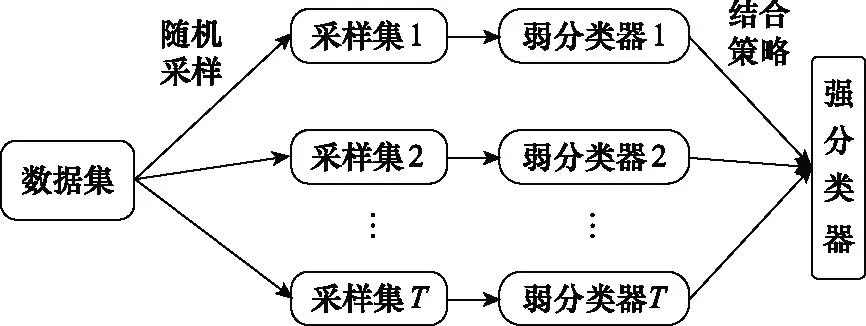
图1 Bagging方法概要图Fig.1 Overview of Bagging method

如图1所示,给定包含n个样本的数据集,先随机取出一个样本放入采样集中,再把该样本放回数据集,使得下次采样时该样本仍有可能被选中,经过n次随机采样操作,得到含有n个样本的采样集。按照以上方法,采样T个含有n个训练样本的采样集,然后基于每个采样集训练出一个分类器。当有样本需要预测时,每一个弱分类器预测出一个结果,通过投票法得到一个强分类器,最终由强分类器预测出样本的类别。

2 目标分类方法

基于RMDLPP的空中目标分类方法主要由两部分组成:① 采用RMDLPP算法对原始数据进行降维;② 使用集成学习分类器对降维后的特征进行分类。总体流程图如图2所示,由图2可将分类方法分为如下几个步骤:

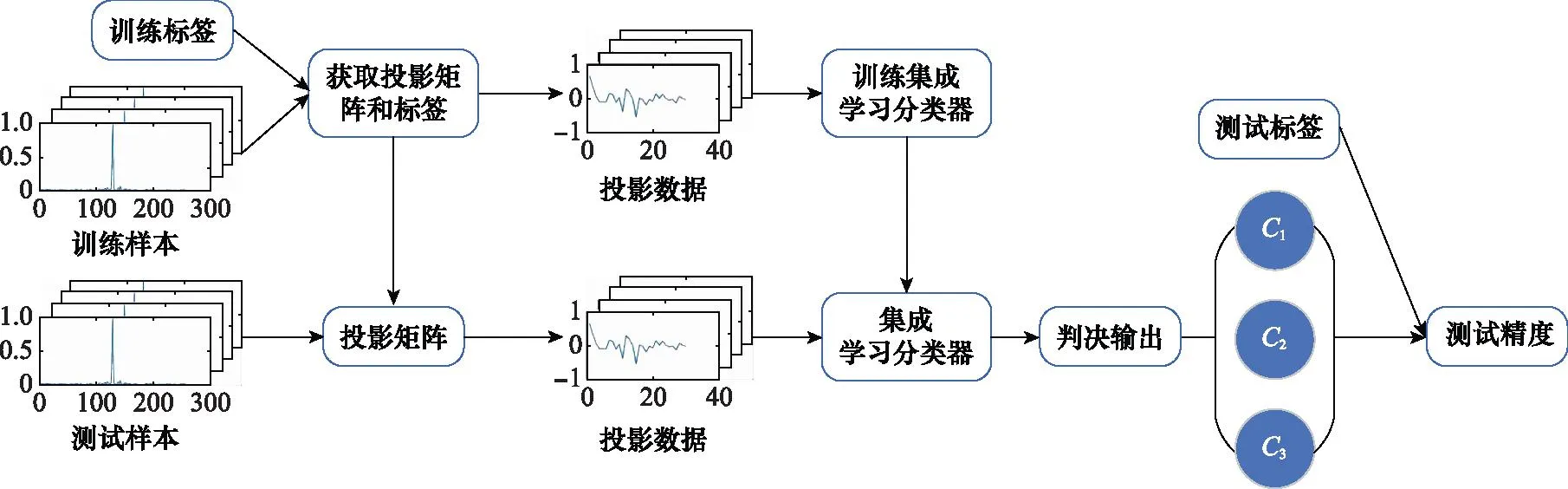
图2 目标分类总体流程图Fig.2 Overall flow chart of target classification

步骤 1输入训练样本和训练标签,训练标签和测试标签均由3类构成,0、1和2代表分别代表3种类别。通过降维方法获得投影矩阵,训练样本与投影矩阵相乘得到降维后的投影矩阵,将投影数据送入集成学习分类器中训练,得到训练好的分类器;

步骤 2将测试数据与投影矩阵相乘,得到测试集的投影矩阵,将测试集的投影矩阵送入训练好的集成学习分类器中,输出判决结果;

步骤 3将判决结果与测试标签进行对比,计算出最终的测试精度。

2.1 降维算法

降维算法主要由计算样本间距离、挑选边界样本点和目标函数优化3部分组成,降维算法的流程图如图3所示。首先,根据改进距离算法计算输入样本之间的距离;然后,从类内挑选k1个类内边界样本点计算类内离散度,并挑选k2个类间边界样本点计算类间离散度;最后,将计算出的类内离散度和类间离散度送入优化后的目标函数中,计算出投影矩阵,并将输入数据与投影矩阵相乘,得到降维后的数据。

图3 降维算法流程图Fig.3 Flow chart of dimensionality reduction algorithm

2.1.1 样本间距离的计算

在数据集分布均匀时,DLPP使用欧氏距离计算能取得较好的降维效果,但如果数据集分布不均匀,欧氏距离往往不能体现数据集的内在特征,从而使降维结果产生一定的形变。高维窄带雷达数据为非线性,样本中数据结构分布并不平均,而是存在孤立点,使用欧氏距离进行权重计算会导致一定的误差,从而影响最终的分类效果。改进欧氏距离算法可以使分布相对集中的区域趋于平均,分布相对稀疏的区域距离减少,具体公式如下:

(8)

式中:m为样本均值;d(xi,xj)表示样本点xi与xj之间的欧氏距离;d(xi,m)和d(xj,m)则为xi和xj与其他样本点的距离的平均值。改进后的算法可增强DLPP算法的鲁棒性,得到相对较好的分类效果。

2.1.2 类内和类间数据的挑选

相似的样本在空间中的位置通常是接近的,同类样本之间具有高度的相似性,因此样本均值很好地反映了同类样本的集中分布,而距离样本最远的几个同类样本点往往具有重要的判别信息,决定了整个类别样本的离散程度。样本均值离同类边界样本越远,表示该类样本越分散;同理,样本均值离同类边界样本越近,表明该类样本越紧凑。

于是可以定义DLPP算法第k类样本中第i个和第j个样本之间的权重为

(9)

样本均值的异类近邻样本通常是易错分的样本,利用这些样本作为类与类之间的边界,既可以有效区分样本的类别,又可以在降维过程中更加关注边界样本点。

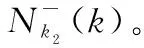
于是可以定义DLPP算法第i类和第j类异类邻近样本之间的权重为

(10)

2.1.3 目标函数的优化

(11)

式中:λ1为迹差的权重系数。式(11)中的前半部分可以转化为如下形式:

WTX(D-S)XTW=WTXL+XTW

(12)

同理,后半部分可以转化为

WTM(E-B)MTW=WTML-MTW

(13)

这里Sk是第k类相似权重矩阵,Dk和E是对角阵,M=[m1,m2,…,mC]∈Rm×C,相应的公式形式为

(14)

(15)

然后,将式(12)和式(13)代入式(11)中,此时的目标函数转化为

(16)

对[λ1XL+XT-(1-λ1)ML-MT]进行特征分解,求出前r个最小特征值对应的特征向量即为投影矩阵。将输入数据与投影矩阵相乘得到降维后的数据X*。

2.2 分类算法

分类算法由以下3部分组成:① 从训练集中随机抽样得到子训练集;② 由子训练集训练得到基模型;③ 对基模型进行预测得到预测结果;④ 通过投票法进行综合得到最终的分类结果。分类算法流程图如图4所示。

图4 分类算法流程图Fig.4 Flow chart of classification algorithm

3 实验结果与分析

本文搭建的网络模型所采用的数据集来自X波段对空警戒雷达,工作频率10 kHz,相关脉冲数为250个。样本由直升机、螺旋桨和喷气式3类飞机组成,其中直升机1 192个、螺旋桨1 435个、喷气式843个,3类飞机的数据维度为256。针对本文研究的样本数量小于样本维度的情况,本文将训练样本逐步增大,直至超过样本维度,为了保证实验的可靠性,选择足够多固定的样本作为测试样本,3类飞机的训练数量和测试数量设置如表1所示。

表1 训练样本选择表Table 1 Training sample selection table 个

如表1所示,设置每类训练样本数量由20至100逐渐增大,直至3类样本之和超过了训练维度256;设置每类样本测试数量为400个固定的样本,这样既能避免因样本分布不均匀带来的偏差,又能进一步保证实验的可信度。

由于降维后特征值的个数对算法的性能影响较大,为了得到较优的算法模型,本文使用一组实验在训练样本数量不同的情况下对降维后的维度进行了选择。另外,完成降维后选择不同的分类器分类,得到的分类精度也会大不相同,本文在特征维度确定的条件下,使用不同的分类器在训练样本数量不断增加观察分类器的变化,以此来选择最佳分类器。最后,使用本文方法与目前较新的4种降维方法进行对比实验,通过分类时间和分类精度的对比,证明了本文所提方法的有效性。

3.1 分类器选择

使用不同的分类器,会有不同的分类效果,本文使用常用的k近邻(k-nearest neighbor, KNN)分类器、贝叶斯分类器、SVM分类器、鉴别分析法分类器和集成学习分类器进行对比分析,随着训练数量的增加,测试精度变化如图5所示。由图5可以看出,随着训练数量的增加,5种分类器分类精度都会随之增加。在训练数量为每类20个时,SVM分类器的分类效果最好,这是由于SVM训练出来的结果由支持向量所决定,少量的支持向量让SVM有了较强的泛化能力,因此SVM结果会优于其他分类器。随着训练数量的增加,集成学习分类器的优势逐步展现,这得益于集成学习分类器采用随机采样和弱分类器投票策略。在随机采样中,由于部分训练样本未被抽取,一定程度上增加了集成学习的泛化能力;由若干个弱分类器投票组成强分类器,极大提升了集成学习分类器在预测时的容错率。从图5可以看出,在训练样本数量为40至100时,集成学习分类器分类准确率均高于SVM分类器,且有逐步将精度差距扩大的趋势,充分展现了集成学习的优势。KNN分类器由于受限于邻域样本个数和每类样本数量的影响,在样本数量较少时分类精度较低,随着训练数量的增加分类精度有所改观,但仍无法与SVM和集成学习相比。贝叶斯分类器受限于样本之间完全独立,分类效果一直处于较低水平。综上所述,集成学习分类器在降维后的分类中具有较好的性能,本文选择以集成学习分类器作为降维后的分类方法。

图5 分类器选择图Fig.5 Classifier selection graph

3.2 挑选类内和类间参数

类内挑选k1个样本点,类间挑选k2个样本点,识别的准确率会随着挑选样本点个数的变化而变化,本文从以下两个实验确定参数k1和k2的选取。

实验 1初步判定k1和k2的取值。分类器选用集成学习分类器,并将每类训练数据设定为80个,参数k2设定为20、40、60和80,识别准确率随k1的变化如图6所示。图6中,k2保持不变,随着k1的不断增加,识别准确率变化的整体趋势是先增大后减小,在k1为40时,识别准确率取得最大值。类内数据点挑选过少,可能会使类内边界表达不充分,挑选过多,类内边界会过于拟合均值附近点,从而导致识别准确率下降,由以上可以得出,类内挑选数量为中间某值时识别准确率达到最佳。当k1不变时,从图6中可以看出,识别准确率最大值大多在k2取40时得到。类间挑选边界点过少,会使类间边界点表达不充分,挑选过多,会使类间边界点向类内中心点拟合。因此,最佳取值也应在中间某点取得。由实验1得出,k1和k2取值为每类训练数量一半时,识别准确率达到最佳。因此,可以初步得出结论,为了使识别准确率达到最佳,k1和k2应当取每类训练数量的一半。

图6 参数k1 和k2变化图Fig.6 Parameter k1 and k2 change graph

实验 2验证k1和k2取每类训练数量一半的正确性。分类器选用集成学习分类器,每类训练数量设置为40、60、80和100,将k2设置为每类训练数量的一半,识别准确率随k1变化的曲线如图7所示。其他参数不变,将k1设置为每类训练数量的一半,识别准确率随k2变化的曲线如图8所示。从图7和图8中可以看出,随着每类训练数量的增加,识别准确率整体呈现增加的趋势;随参数k1和k2的增加,识别准确率整体都呈现出先增后减的变化趋势。每类训练数量增加,算法学习到的特征更加丰富,识别准确率会进一步提升。从图7中可以看出,当每类训练数量为40、60和100时,三者k1挑选数量均在每类训练数量的一半达到识别准确率的最大值,每类训练数量为80时,也达到了相对较大值。虽然存在一定的波动,但整体可以验证,k1取每类训练数量的一半的正确性。与图7相似,图8中也展示出当k2挑选数量为每类训练数量的一半时,识别准确率达到相对较大值,进一步验证了k2取每类训练数量的一半的正确性。

图7 类内参数k1选择图Fig.7 Intra-class parameter k1selection graph

图8 类间参数k2选择图Fig.8 Inter-class parameter k2selection graph

3.3 挑选降维后的特征维度

经过测试,特征维度过大或者过小分类精度均会维持在较低水平,因此本文根据经验将维度区间设置在10到100的范围内,从以下两个实验来确定降维后特征维度的选取。

实验 1初步判定降维后的特征维度取值。由于训练数量为每类20个时,降维后的样本数量总和60依然小于特征维度100,因此本文将训练数量设置为40至100。分类器选用集成学习分类器,在其他条件不变的情况下,分类识别正确率随特征维度的变化如图9所示。从图9可以看出,在特征维度不变时,随着训练数量的增加,整体精度呈现上升趋势;在每类训练数量不变的条件下,随着特征维度的增加,训练精度呈先上升后下降的趋势,在20至70之间均维持较高分类精度,并且在特征维度为30时达到识别精度的最大值。当样本降维后保留的样本维度过少时,会导致关键信息缺失,从而无法正确进行分类。同样,当降维后保留的样本维度过多时,会由于降维不充分而导致信息冗余,进而干扰分类的准确率。通过实验得出,降维后的特征维度为30可以达到最优识别效果。

图9 分类识别正确率随特征维度变化图Fig.9 Classification recognition accuracy varies with feature dimension

实验 2使用不同的分类器验证降维后特征维度取值的正确性。在其他条件不变的情况下,使用不同的分类器在每类数据量为100时进行实验,分类识别准确率随特征维度的变化如图10所示。由图10可以看出,随着特征值个数的不断增加,5类分类器分类准确率整体呈现出先增后减的变化趋势。对于贝叶斯分类器、集成学习分类器和SVM分类器,在降维后特征值取30时达到最佳识别效果;对于KNN分类器和鉴别分析法分类器分别在降维后特征值取40个和20个时取得最优值,在降维后特征值个数取30个时也取得了次优的识别结果。因此,将降维后特征值个数取30个,可以使不同的分类器均达到相对较优的效果。

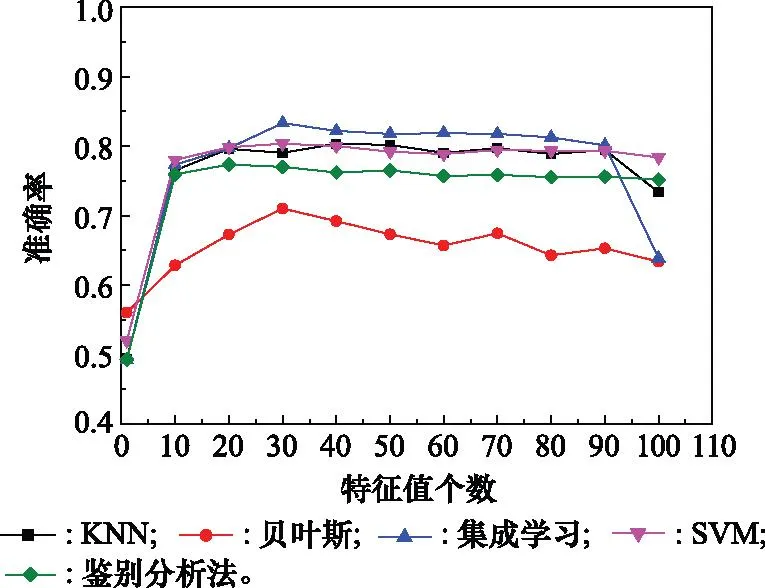
图10 特征维度选取验证图Fig.10 Feature dimension selection verification graph

3.4 对孤立点鲁棒性的验证

在挑选数据点时,类内边界点和类间临界点大多数为孤立点。因此,在挑选类内和类间参数时,不同的距离计算方法对识别准确率的影响幅度,能很好地反映对孤立点的鲁棒性情况。实验中,分类器采用集成学习分类器,并将每类训练数据设定为80个,参数k2设定为40和80,距离计算方法分别设定为欧氏距离法和改进欧氏距离法,识别准确率随k1的变化如图11所示。

图11 孤立点鲁棒性验证图Fig.11 Isolated points robustness verification graph

从图11中可以看出,在k1和k2相同的条件下,使用改进欧式距离的识别准确率要高于使用欧氏距离的识别准确率,这主要是由于改进欧氏距离将样本均值融入到距离的计算中,增加了边界样本识别的准确率。当类间挑选个数k2确定时,使用欧式距离法在最高点向两侧下降的速度要大于改进欧式距离法,这是因为当类内挑选数据较少或较多时,类内边界样本点包含在挑选数据中,使用改进欧式距离法可使类内边界样本向均值处靠拢,增加样本类别之间的可分性,因此识别准确率下降的较慢。同理,当类内参数k1确定时,相比于欧氏距离法,使用改进欧式距离法也会使识别准确率在最高点向两侧下降的速度更慢,这进一步证明了改进欧式距离法可以增加算法对孤立点的鲁棒性。

3.5 5种改进方法对比

在确定RMDLPP方法的关键参数和分类器后,将RMDLPP方法与PCA-LPP、EDLPP[25-26]、SMOTE-DLPP[27]、LPPMDC[28-29]等方法进行对比分析,随着训练数据的增加测试数据精度的变化如图12所示,测试数据所消耗的时间变化如图13所示。

图12 精度随训练数量变化图Fig.12 Accuracy varies with number of trainings

图13 时间随训练数量变化图Fig.13 Time varies with number of trainings

从图12和图13可以看出,随着训练数据的增加,RMDLPP方法始终维持最高的识别精度,且测试数据所消耗的时间始终维持较低水平。对于PCA-LPP算法,由于在做PCA时进行了线性降维,再通过LPP做非线性降维时可能会丢失一部分关键信息,导致精度无法提高到理想水平。EDLPP算法由于在距离计算时使用欧氏距离,对离群点较为敏感,且对边界数据的区分能力有限,所以分类精度处于较低水平。使用SMOTE-DLPP方法时,先对数据进行扩充处理,当训练数据个数大于数据维度时进行DLPP降维处理,由于在数据扩充时使用了神经网络,一定程度上增加了时间成本,精度也并不占优。LPPMDC方法将迹商改为迹差,也能得到较高的精度,且时间成本也相对较低,然而LPPMDC为无监督学习方法,无法充分利用已知的类别信息,因此无法达到最佳分类效果。RMDLPP算法对边界进行清晰化处理,使得数据的可分性增加,对欧氏距离进行改进,使得对离群点的鲁棒性增加,进而增加了分类精度;在对边界进行清晰化处理时,由于只处理了部分边界数据,因此一定程度上缩减了测试所用的时间。

4 结 论

本文提出来了一种基于RMDLPP的目标分类方法,对窄带雷达空中目标进行降维和分类。通过对目标函数进行优化,解决了样本数据量小于样本维度数时出现的类内离散度矩阵奇异问题;通过引入边界Fisher分析,解决了窄带雷达数据边界区分困难的问题;通过改进样本间的距离计算公式,解决了DLPP算法对孤立点较为敏感的问题。通过X波段对空警戒雷达实测数据的对比实验表明,在样本量大于40时,本文所提方法精度均维持在80%以上,这进一步证明了本文所提方法处理高维数据的能力。