城市轨道交通列车轮轨垂向力测量方法*

2024-03-27陈鹏涛漆泰岳覃少杰

城市轨道交通研究 2024年3期

陈鹏涛漆泰岳梁孝雷波覃少杰

(1.西南交通大学交通隧道工程教育部重点实验室, 610031, 成都; 2.西南交通大学土木工程学院, 610031, 成都)

城市轨道交通运营中往往会出现大量的隧道病害问题,如盾构区段的管片不均匀沉降、道床-管片剥离病害等。列车轮轨力作为各种病害的主要成因[1-2],对其进行监测是研究隧道病害动力响应的重要环节。现有对轮轨垂向力的监测方法研究成果较多,如挠度法、加速度法、剪力法、弯矩差法、轨腰压缩法及支撑反力法等。文献[3]研究了高速铁路列车在车轮失圆和轨面波磨等条件下的轨道结构受力。文献[4]利用测力钢轨设计了连续测试轮轨力系统,并通过数值模拟方法对轮轨力计算方程和相关参数进行了研究。文献[5]利用电阻应变片分别对钢轨所受横向力和垂向力进行了测试,推荐剪力法为监测效果较好的办法。文献[6]基于剪力法对轮轨垂向力测试系统进行了设计,并对应变计输出数据的降噪办法进行了研究,提出了较准确的获得轮轨垂向力监测数据的方法。文献[7]研究了钢轨受到水平力和垂直力时的应变分布,比较分析了各种轮轨竖向力监测方法的优缺点及实用性,得到了应变片测点布置和组桥的最佳方案,并提出了基于剪力法和轨腰压缩法的轮轨垂直力连续测量方案,通过有限元仿真计算得到,当垂向电桥在钢轨两侧布点完全对称时,钢轨受到的横向力不影响垂向测试电桥的输出结果。文献[8]采用测量车轮压力的方法测得轮轨力,并通过试验台验证了该方法的可行性。文献[9]根据成都地铁9号线运营现状计算得到了列车单轮激振力函数,确定了现场监测频率应不低于振动频率的10倍。

轮轨力现场监测通常采用在施工时预埋土压力盒测定道床压力的方法。为保证城市轨道交通线路安全运营,在不破坏现有轨道结构的条件下,选择钢轨压力来反映轮轨垂向力。根据成都地铁运营现状,以弯矩差法为理论基础,通过数值模拟软件对列车动荷载下钢轨的动力响应进行计算,并与静荷载计算结果进行对比。选取钢轨测点,在室内静荷载标定试验中对其进行测试,从而确定了标定系数。该方法对现场监测的开展具有指导作用,为城市轨道交通列车正常运行下轮轨垂向力的实时监测奠定了技术基础。

1 工程背景

成都地铁7号线(以下简称“7号线”)在运营过程中出现了500余处盾构区段道床-管片剥离病害。本研究以7号线道床剥离病害为研究对象,监测列车运行过程中产生的轮轨垂向力。

7号线列车采用6节编组A型车,设计速度为80 km/h。根据DBJ 51/T 074—2017《成都市地铁设计规范》要求,车辆宽度为3.0 m,拖车长度为23.56 m,动车长度为21.88 m,列车总长度为176.80 m。7号线采用60 kg/m的U75V热轧钢轨。正线铺轨时,常规段扣件组数为1 600组/km,即扣件的平均间距为0.625 m;加强段扣件间距为0.6 m。本研究选择7号线茶店子站—一品天下站下行区间。经现场调查,加强段扣件铺设间距采用0.6 m,所用扣件类型为DZIII型。

2 轮轨垂向力测量原理

采用钢轨受力分析的方法对轮轨垂向力进行测量。将钢轨简化为离散弹性支撑梁模型,采用弯矩差法对其进行受力分析。图1为基于弯矩差法的钢轨垂向力测量示意图。

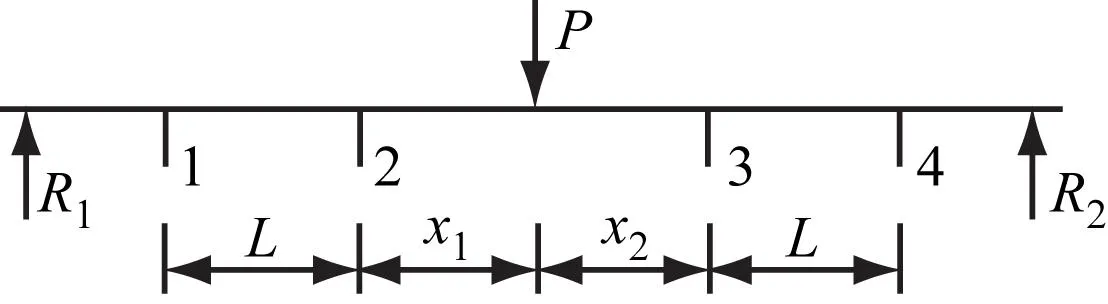
a) 垂向力作用于轨道跨中

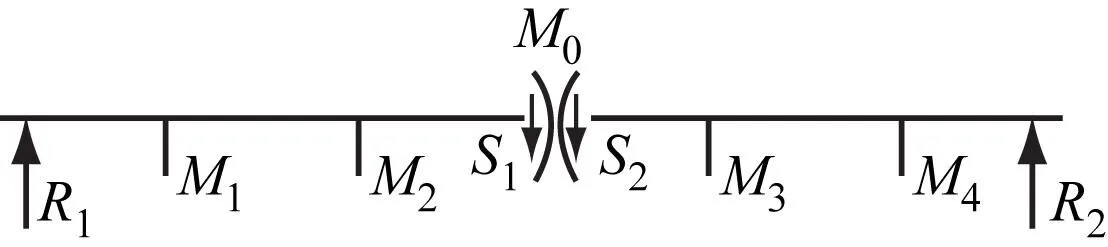
b) 垂向力作用处截面隔离体受力分析

由平衡条件可得:

(1)

式中:

E——钢轨弹性模量;

W——抗弯截面系数;

ε——垂向力作用点沿钢轨行车方向的应变。

3 轮轨垂向力数值模拟分析

在弯矩差法中,列车动荷载作用在钢轨跨中时产生的弯矩最大,且弯矩最大值发生在跨中位置。由于钢轨下表面和道床板之间的空隙狭小,难以采用应变计固定,因此,需将应变计布置在轨底上表面或轨腰的位置,且具体的布点和测量方向采用数值模拟的办法进行确定。

本文采用ANSYS有限元软件,以60 kg/m钢轨为基础,建立如图2所示的钢轨有限元模型。其中:轨枕间距为600 mm,共68 694个节点、53 704个单元。钢轨采用SOLID185单元,其弹性模量取206 GPa;扣件对钢轨的作用采用弹簧约束COMBIN14单元代替,扣件刚度为50 kN/mm,扣件阻尼为75 kN/(m/s);钢轨两端约束x方向和z方向位移。

图2 钢轨有限元模型

3.1 静荷载模拟分析

根据弯矩差法中的荷载施加方式,在钢轨跨中顶面位置分别施加50 kN、100 kN、150 kN、200 kN的静荷载。选取施加200 kN静荷载时的计算结果,提取沿钢轨方向即z方向的钢轨应力云图(见图3)。从图3可以看出:钢轨的最大应变发生在跨中位置。图4为钢轨跨中截面节点编号。图5为静荷载为200 kN时钢轨跨中截面节点沿z方向的应变曲线。

图3 静荷载为200 kN时钢轨沿z方向的应变云图

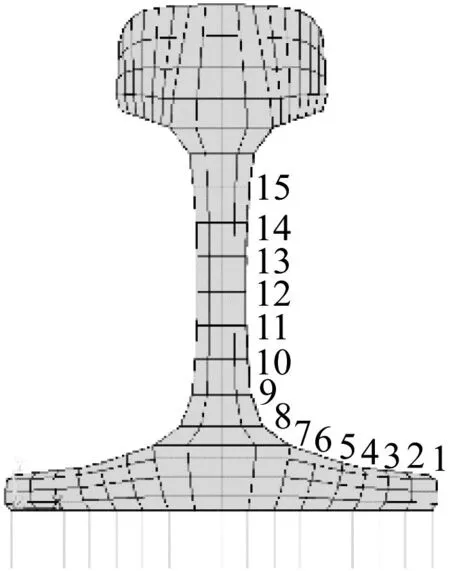
图4 钢轨跨中截面节点编号示意图

从图5中可以看出:钢轨z方向的应变由节点1到15依次减小。相较于节点1粘贴应变片困难,节点2位置最适合作为应变测量点布置应变计。提取静荷载分别为50 kN、100 kN、150 kN时的计算结果。节点2处钢轨沿z方向的应变-垂向力关系曲线,如图6所示。从图6可以看出:节点2处钢轨的应变随垂向力线性增加。K为0.644 1×106kN,故可初步选择节点2位置为应变测量点。

图5 静荷载为200 kN时钢轨跨中截面节点沿z方向的应变曲线

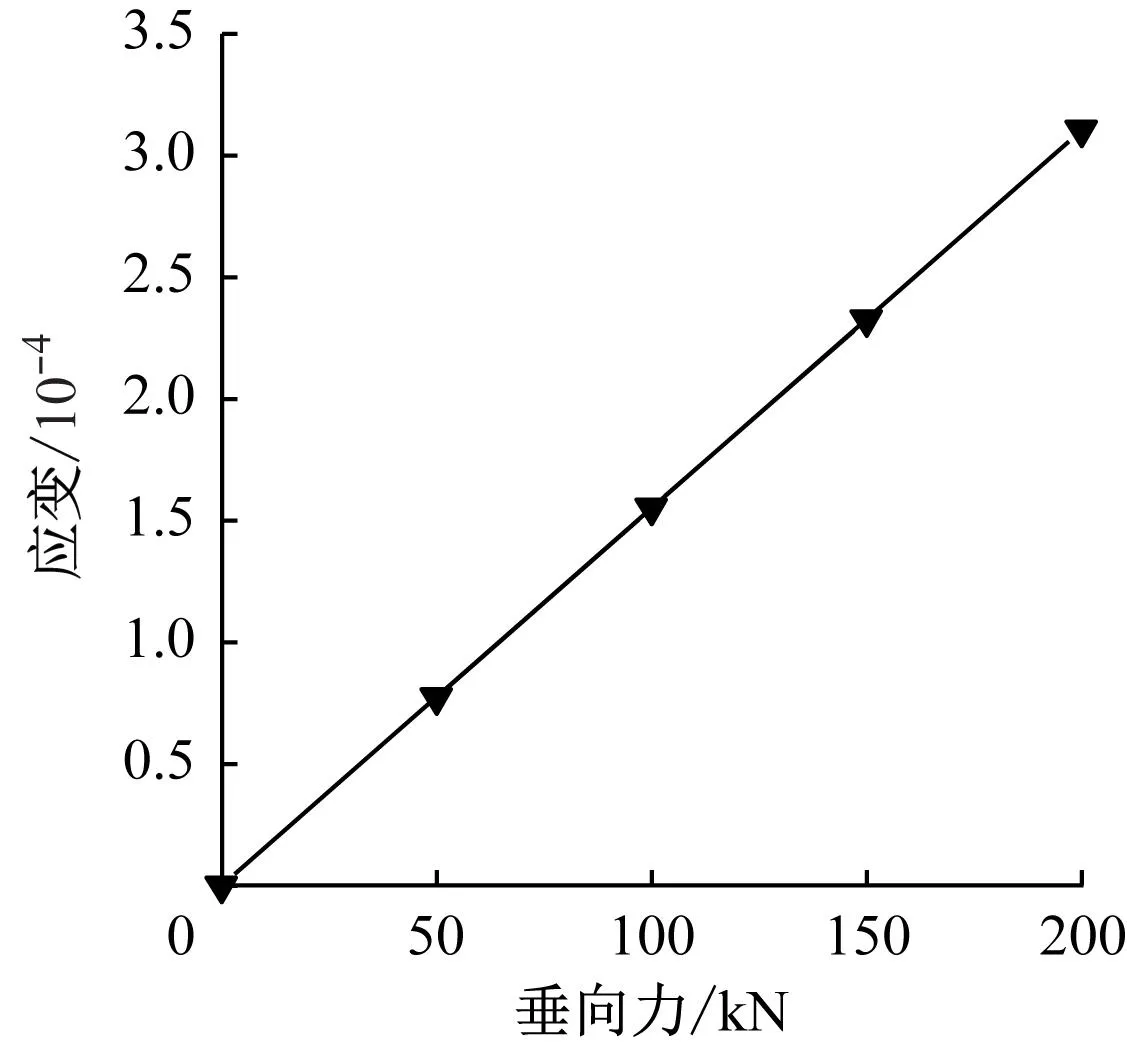
图6 节点2处钢轨沿z方向的应变-垂向力关系曲线

3.2 列车动荷载计算与模拟分析

列车行驶中产生的激振力为动荷载。在进行动荷载分析时,需考虑扣件阻尼的影响,故需对模型施加动荷载以验证静荷载分析的合理性。

3.2.1 列车动荷载计算

根据E.Winkler等人提出并完善的连续弹性基础梁模型,对7号线列车运行时钢轨所受激振力进行计算。A型车转向架中心距为15.7 m,车辆固定轴距为2.5 m,转向架最短中心距即单轴动荷载作用最短间距为6.18 m。扣件间距为0.6 m,远小于单轴动荷载间距,故可将单轴动荷载作为钢轨跨中荷载进行计算。

采用列车轮轨激振力模拟动荷载,列车垂向激振力[10-11]为:

(2)

式中:

p0——单轮静荷载;

m0——列车簧下质量;

ωi——不平顺振动波长的圆频率;

g——重力加速度;

Li——典型波长;

v——列车运行速度;

αi——典型矢高;

t——时间。

A型车单节车厢空载质量为38 t,最大载客量为3 596人。以乘客平均质量60 kg计算,单节车厢满载质量约为65 t,故单轴静荷载为162.425 kN。选取p0=81.2 kN,m0g=0.75 kN。根据英国轨道几何不平顺管理值[9],分别取L1=10 m,α1=5 mm,L2=1 m,α2=0.3 mm,L3=0.5 m,α3=0.1 mm,v=80 km/h,代入式(2)计算得到单轮垂向激振力F(t)(单位N):

(3)

3.2.2 列车动荷载模拟

马铃薯浇水采用深沟浅灌，水不得漫过垄面，幼苗期由于植株小需水量较少，无需浇水；块茎形成期直至增长期要及时灌溉，此时马铃薯处于需水临界期，需要足够水量；开花期至成熟期气温升高，要适当浇水以防止土壤干旱，收获前20天停止浇水。

在钢轨跨中顶面位置施加F(t),设定荷载步终止时间为1 s,荷载子步数为500。选择节点2位置输出应变时程曲线,如图7所示。从图7可以看出:在受力达到稳定后,节点2处钢轨沿z方向的应变时程变化规律和F(t)相似。当t=0.592 s时,应变达到最大值,此时F=90.924 kN,εz=140.633×10-6;当t=0.804 s时,应变为最小值,此时F=71.398 kN,εz=111.624×10-6。

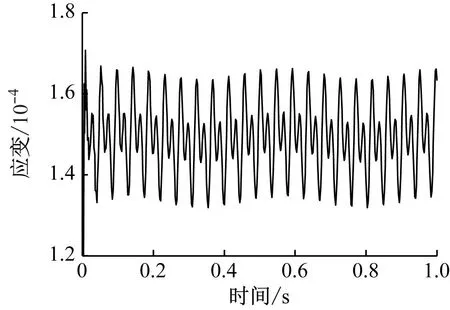
图7 动荷载下节点2处钢轨沿z方向的应变时程曲线

节点2处钢轨的垂向力沿z方向的应变散点图,如图8所示。从图8可以看出:经线性拟合后,曲线斜率为1.548×10-6/kN,转换为K=0.646×106kN。受扣件阻尼影响,K略大于静荷载作用下的计算结果,偏差仅为0.3%。

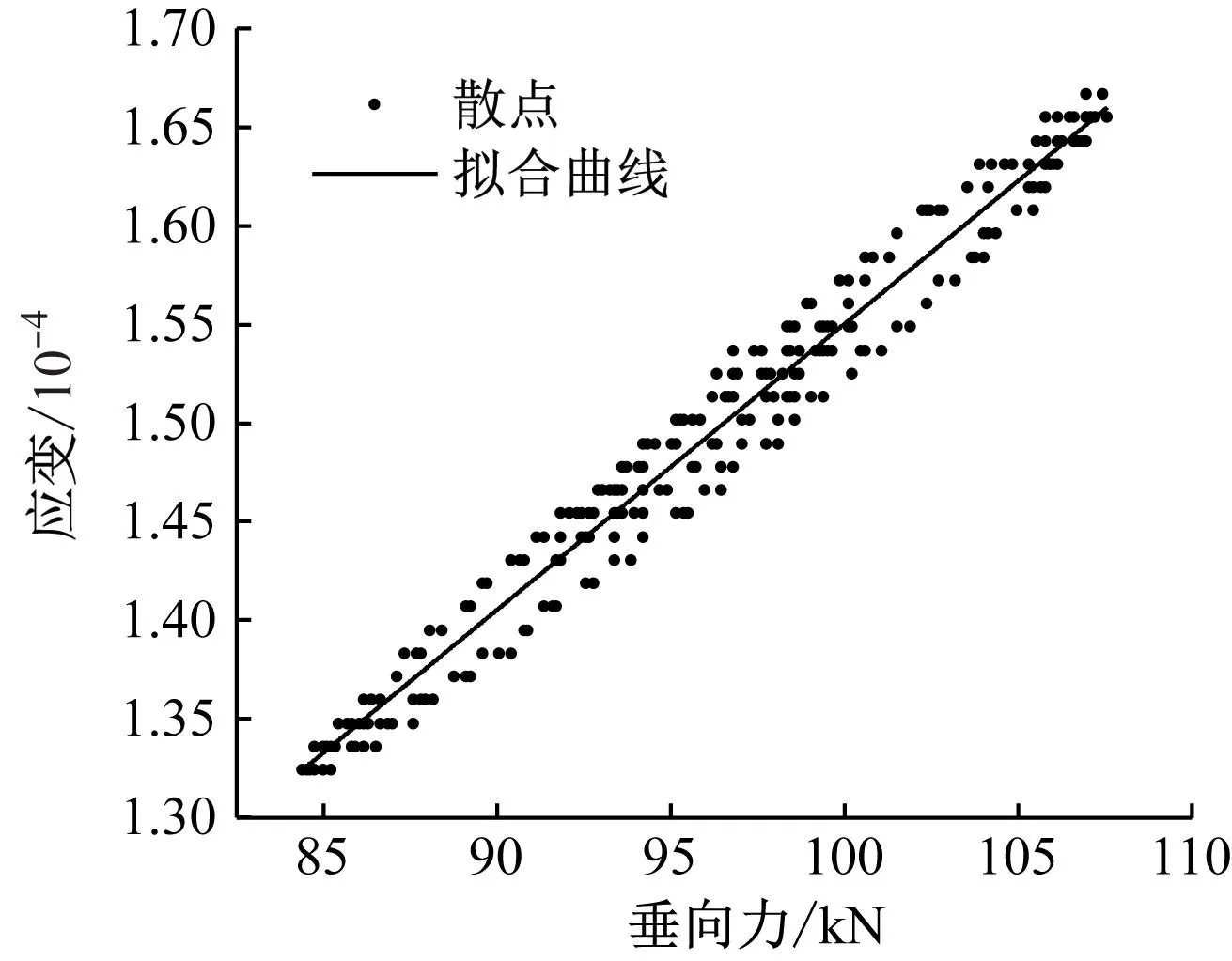
图8 节点2处钢轨沿z方向应变-垂向力关系曲线

综上,采用弯矩差法测量轮轨垂向力时,测点位置可选择在钢轨跨中位置的轨底上表面边缘,即图5所示的节点2位置。分别通过施加静、动荷载对钢轨进行数值模拟,得出扣件阻尼对计算结果的影响较小,求得K偏差仅为0.3%。因此,可在室内进行标定试验,采用施加静荷载的方法验证并确定K。

4 轮轨垂向力标定试验

4.1 测量系统组成

在钢轨标定试验中,测量系统如图9所示。该系统主要由电阻式表面应变计、USB6005数据采集卡及数据采集软件组成。测量所用的电阻式表面应变计采用全桥电路连接并进行封装设计,可消除温度效应和零漂影响。表1为测量所用两支电阻式表面应变计的主要参数。USB6005数据采集卡连接至计算机,其可以识别到应变计传出的电信号,并将采集到的电信号数据通过自主开发的采集软件显示并保存,以此得到测点的应变情况,从而确定钢轨所受垂向力。

图9 测量系统构成

表1 电阻式表面应变计的主要参数

4.2 试验加载方案

受试验场地和加载设备等条件的限值,标定试验采用1根长2 m的钢轨进行3跨布置。试验用钢轨及其应变计布置方式如图10所示。两支应变计采用强力胶水紧贴轨底上表面边缘对称布置。

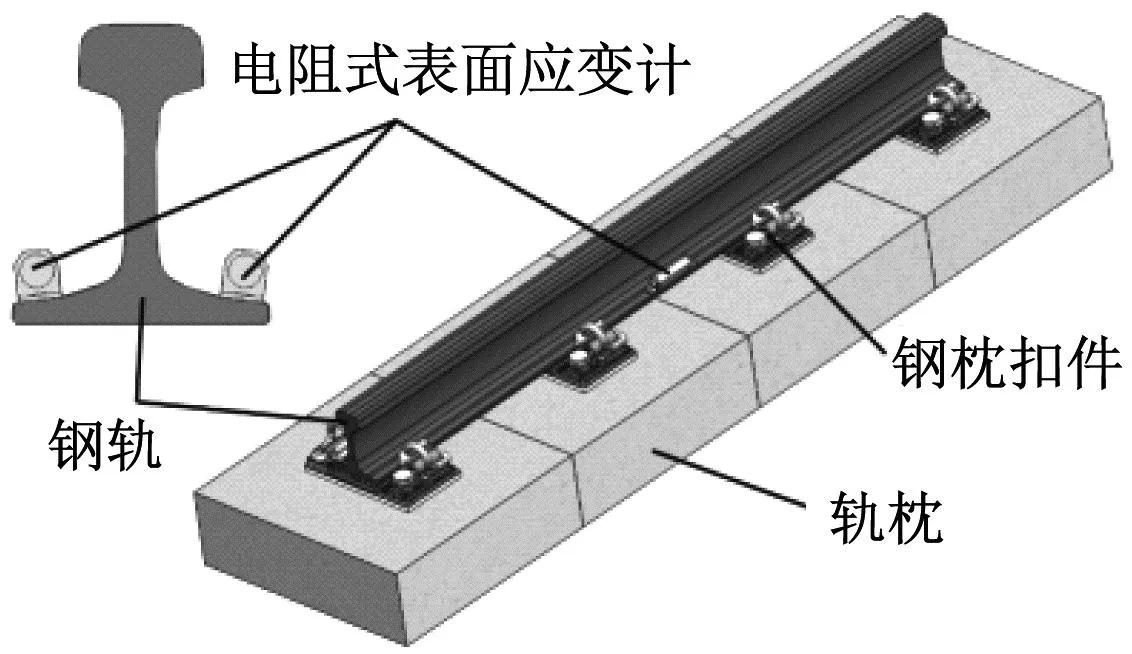
图10 试验用钢轨及其应变计布置方式

本次标定试验采用多通道电液伺服疲劳加载系统(以下简称“电液伺服加载系统”)进行加载。图11为标定试验加载台,应变计按图10方式粘贴在钢轨两侧。以0、50 kN、100 kN、150 kN、200 kN、220 kN逐级加载,每级加载时间为100 s,达到目标荷载后保持50 s,加载完成后快速卸载。USB6005数据采集卡与两支应变计直接连接,进行双通道数据采集,采集频率取100 Hz。

图11 标定试验加载台

4.3 试验结果分析

卸载完成后,USB6005数据采集卡所收集的钢轨电压变化趋势如图12所示。从图12可以看出:两支应变计的输出电压呈阶梯形上升,且卸载后快速恢复到接近初始状态;由于在加载过程中,电液伺服加载系统并不能按设定值完全平稳地保持荷载大小,因此曲线呈现一定程度的波动,但总体符合静荷载随加载时间的变化规律。

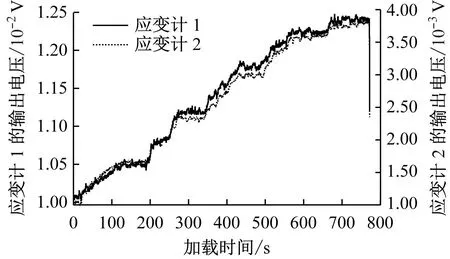
图12 不同应变计输出的钢轨电压时程曲线

根据表1中应变计的主要参数,计算得出不同应变计测得的钢轨应变随垂向力变化曲线,如图13所示。从图13中可以看出:应变计的输出电压和测定应变基本与施加的垂向力呈线性相关,这与式(1)相符;应变计1的曲线斜率为1.427×10-6/kN,应变计2的曲线斜率为1.816×10-6/kN,换算为K分别为0.701 0×106kN和0.551 0×106kN,将两者取平均值,则K为0.626 0×106kN。