地铁隧道砂土劈裂注浆加固机理分析*

秦鹏飞 钟宏伟

(1．黄河科技学院工学部, 451001, 郑州; 2.重庆交通大学水利水运工程教育部重点实验室, 400074, 重庆;3.郑州铁路职业技术学院铁道工程学院, 451010, 郑州)

在劈裂注浆过程中,砂层结构在注浆压力的作用下遭到破坏,劈裂通道在砂土内部交错、扩展[1-5]。劈裂注浆产生的浆脉改善了砂砾石层的结构形态,显著提升了砂层的防渗与承载性能[6-7]。文献[8]发现砾石土和砂土多序次注浆加固中,土体压缩应变-应力曲线和浆液劈裂扩散轨迹呈规律性的动态变化;文献[9]指出砂层中黏性土含量是影响劈裂注浆效果的重要因素,砂层自身压密特性、浆液扩散形态均随黏性土含量发生明显改变;文献[10]分析了脉动注浆与稳压注浆的加固机制和加固效果,认为脉动劈裂注浆应力传递更均匀,其对局部地层抬升具有更强的可控性;文献[11]基于流体体积法和弥散裂缝模型编制有限元程序,分析了土性参数、注浆压力、注浆速率及注浆孔埋深等因素对劈裂注浆加固效果的影响;文献[12]认为浆液压力在孔口及远端处急速衰减,而在中间区段呈稳定变化趋势,浆液压力的时空分布决定着劈裂通道宽度的分布。

上述研究大多基于弹塑性力学的基本理论,假定劈裂注浆中劈裂裂缝一次成型且宽度不变。实际上劈裂注浆是浆液流场与砂土应力场的耦合过程,浆土界面存在复杂的流固耦合效应,因此分析计算中需考虑这种动态作用。本文以宾汉流体为代表对浆液流场的基本特征进行了分析;采用均质各向同性的弹性假定,推导了劈裂通道宽度、浆液压力的时空变化方程;通过调节浆液黏度、砂土刚度等参数,对砂土劈裂注浆基本规律进行了探讨。结合重庆地铁10号线(以下简称“10号线”)某暗挖区间进行检验验证,对指导实际注浆设计、施工具有一定参考。

1 劈裂注浆理论

1.1 基本假定

为便于分析计算,本文对砂土劈裂注浆模型做如下假定:①砂土为均质、各向同性的弹性体,压密变形表现为线性变形,注浆浆液为宾汉水泥浆液,水灰比在扩散路径上不变;②劈裂通道上下侧壁与中轴线平行,浆土界面上的浆液压力近似沿铅垂向;③注浆压力为脉冲式压力,压力大小、间歇时间保持恒定;④浆液在扩散过程中不发生流失,严格满足质量守恒方程,考虑重力对浆液扩散形态的影响[13-14]。砂土劈裂注浆机理见图1。

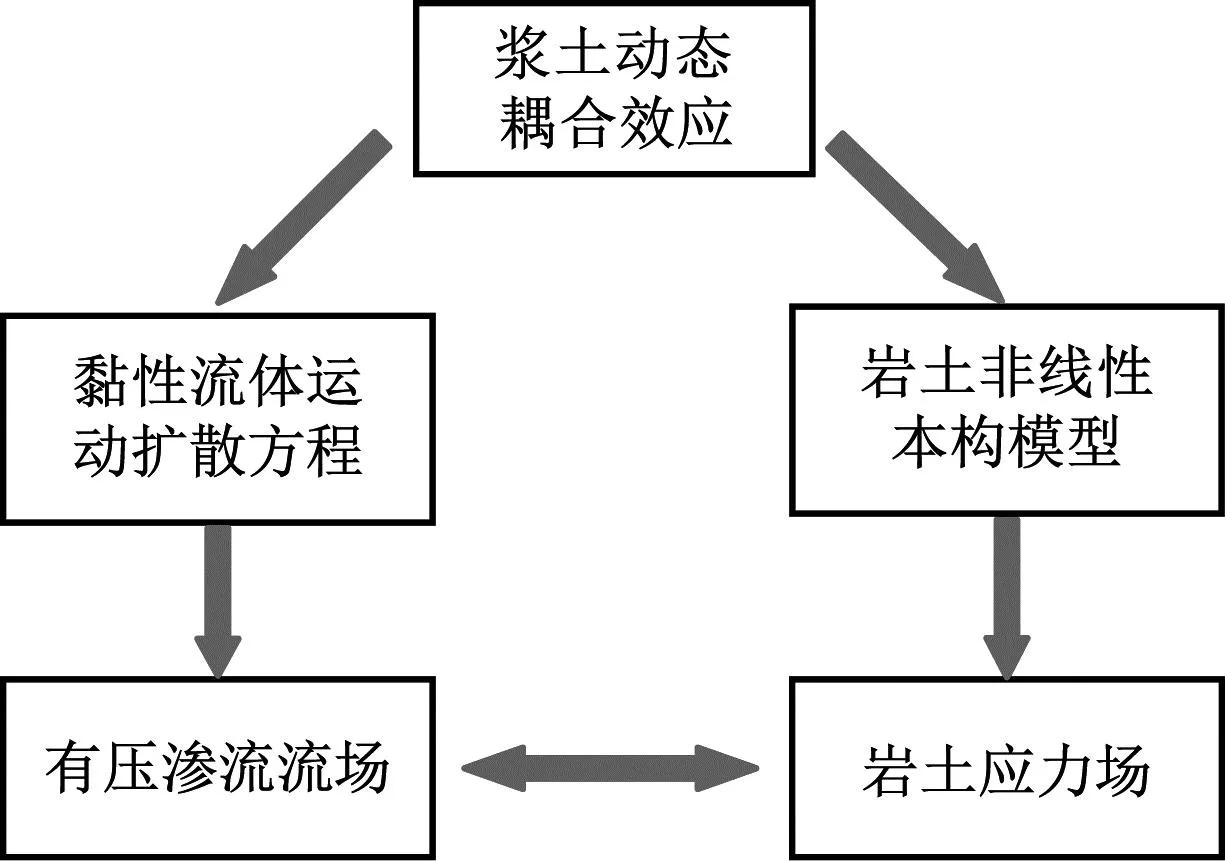
a) 浆土动态耦合机理

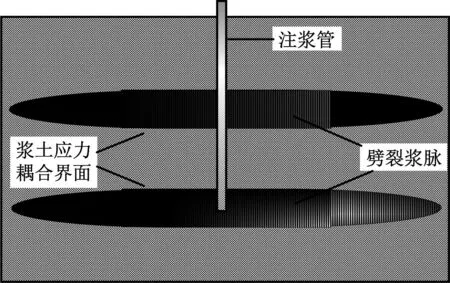
b) 劈裂扩散模型

1.2 起劈压力与劈裂通道扩展压力

砂土劈裂注浆力学机制非常复杂[15-17]。为简化分析,将钻孔应力状态进行对称分解。砂土劈裂注浆力学机理分析见图2。设注浆孔内连续施加稳定的注浆压力为p,注浆孔半径为c0,孔外承受水平向最大主应力为σ1,竖向最小主应力为σ3,砂土单元环向拉应力σβ为:

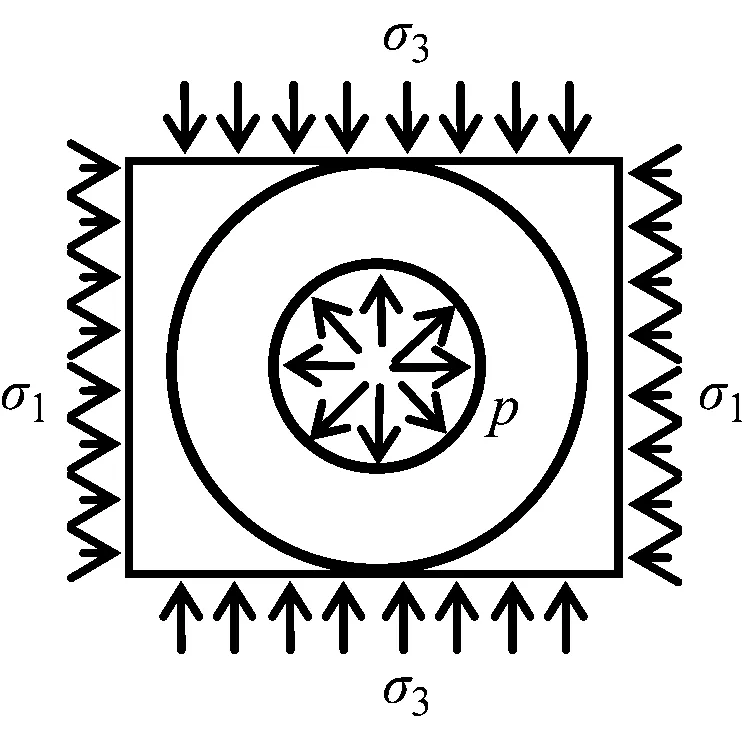
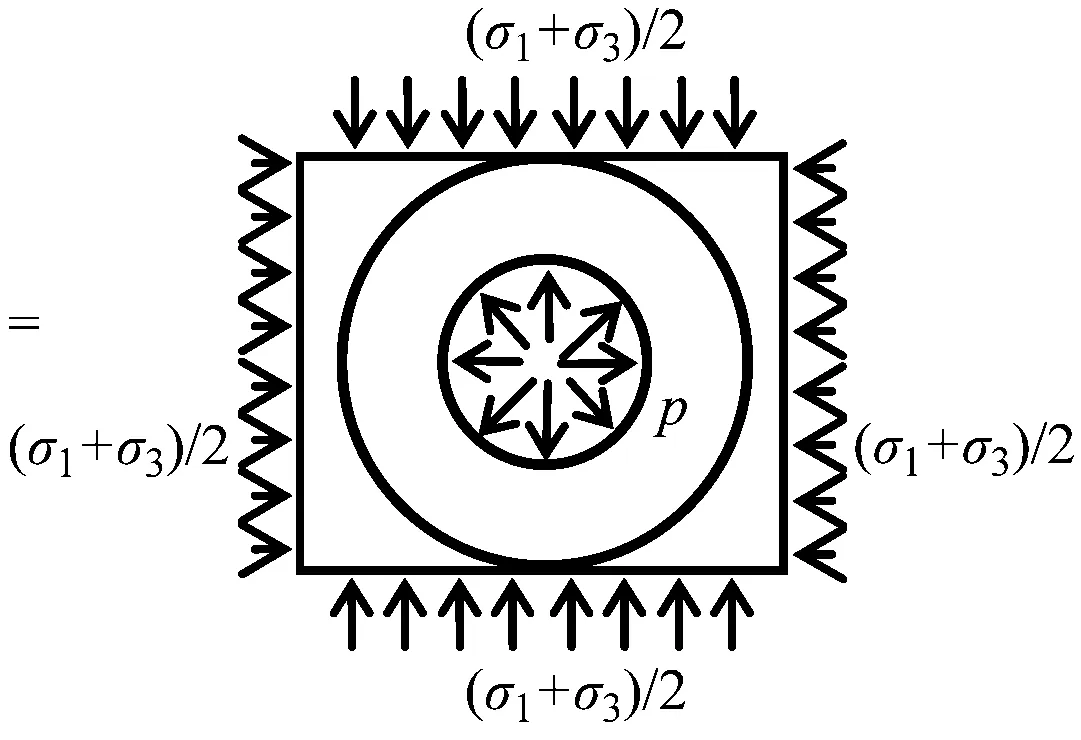
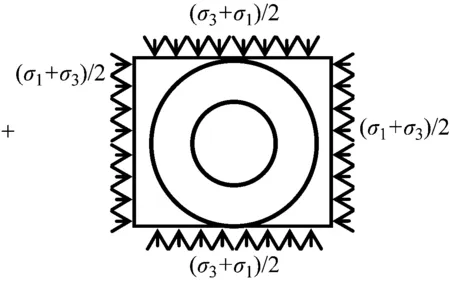
图2 砂土劈裂注浆力学机理分析

(1)

式中:

β——任一点在钻孔极坐标系下的极角;

c——任一点在极坐标下的半径。

钻孔周围应力状态随注浆压力增大呈复杂变化。当注浆压力达到临界值时,砂土结构产生贯通破坏,起劈压力pk为:

pk=4σ3+σe-σ1

(2)

式中:

σe——砂土极限抗拉强度。

劈裂发生后砂土应力持续调整,伴随着一系列受剪、受拉破坏,劈裂裂缝在砂土内四处扩展。劈裂扩展压力pu为:

(3)

式中:

pu——断裂效应下劈裂扩展压力;

V(s/c0)、W(s/c0)——断裂力学计算函数,s为劈裂扩展有效长度;

γ0——劈裂扩展影响系数。

在中密-松散结构的富水砂层中,劈裂注浆下浆液扩散半径可达 22～40 m。浆液劈开砂层后注浆压力有所衰减,随着后续能量的注入,浆液压力在扩散通道上呈现起伏跌宕的状况。注浆压力-浆液扩散距离关系曲线见图3。

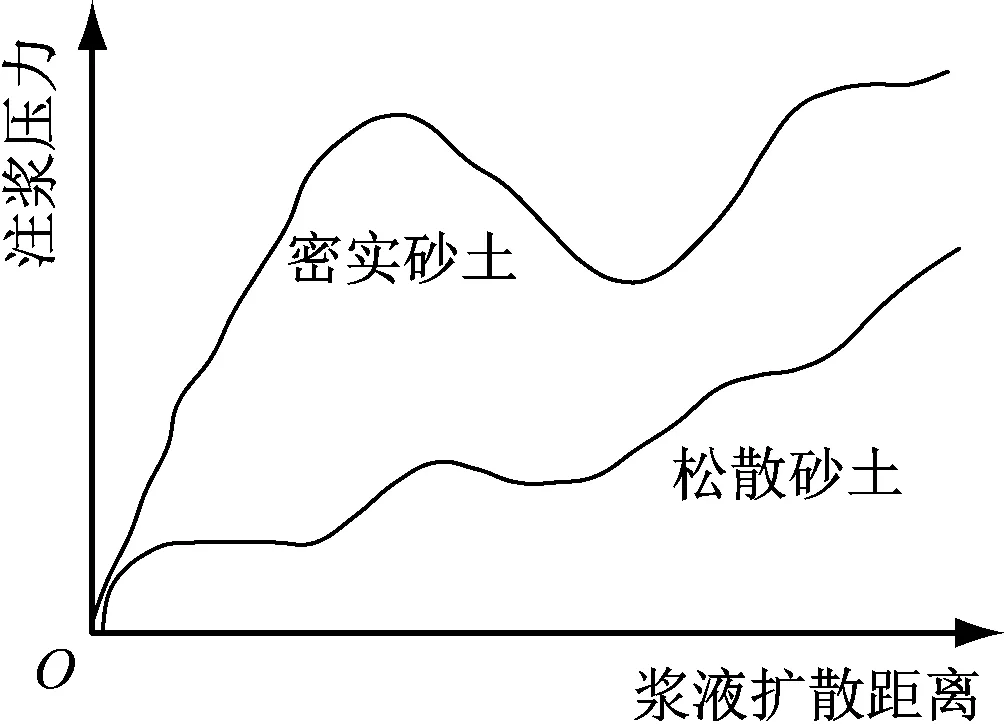
图3 注浆压力-浆液扩散距离关系曲线

1.3 劈裂通道内部浆液扩展特征

劈裂注浆过程中浆土界面存在动态耦合作用,浆液在辐射扩散时对砂层产生压应力,砂层对辐射扩散的浆液产生一定阻抗。劈裂注浆中浆土耦合作用分析模型见图4。

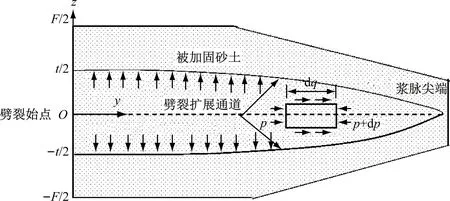
a) 劈裂扩展机制模型

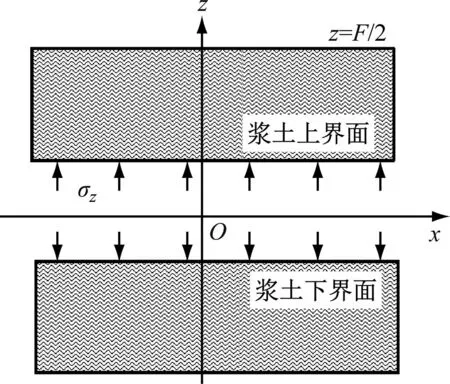
b) 弹性变形计算模型

根据黏性流体流动机理,劈裂通道上浆液微元体受力平衡方程为[18-19]:

τdq+hdp=0

(4)

式中:

τ——黏性流体内部剪切应力;

dq——微元体分析计算长度;

h——劈裂通道中心线下半部分微元体高度。

式(4)经恒等变形可得:

τ=-hdp/dq

(5)

宾汉型流体的本构方程:

(6)

式中:

τf——静切力;

ηg——塑性黏度;

v——浆液流速。

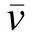
(7)

由浆液质量守恒和密度守恒假定,得到劈裂通道内的注浆压力变化为:

(8)

式中:

λ——注浆速率。

1.4 劈裂通道宽度计算

以通过劈裂通道中心线的水平面为Oxy平面,以竖直平面为Oxz平面建立坐标系,进行劈裂机理分析。考虑对称性,砂土在x、y方向均不产生位移,仅在z方向存在位移[20-25]:

ax=ay=0,az=a(z)

(9)

式中:

ax、ay、az——砂土分别在x、y、z方向上的位移。

砂土产生压密变形的应力σh与注浆压力有关,其大小为σh=p-pu。根据弹性力学的基本原理,砂层压密变形后其铅垂向应变εz为:

(10)

式中:

E——弹性模量;

μ——泊松比。

考虑浆土耦合效应,砂土铅垂向的应力σz=pu-p。对式(10)两侧进行积分、变换,可得az:

(11)

式中:

B0——积分常数,可由初始应力、位移条件求得。

砂土劈裂注浆存在有效影响范围,砂土竖向位移在浆土应力接触界面上最大,并沿该界面上下两侧逐渐衰减。砂土最大竖向位移amax为:

(12)

劈裂通道总宽度在浆液扩散半径上动态变化,为上下通道宽度之和。劈裂通道总宽度与注浆压力的关系为:

㉔VoBkuhle A．Rechtsschutz gegen den Richter，Zur Integration der Dritten Gewalt in das verfassungsrechtliche Kontrollsystem vor dem Hintergrund des Art，1993，S．74．

(13)

式中:

J0——砂土刚度参数。

1.5 劈裂通道宽度及浆液压力空间分布方程

考虑劈裂通道宽度与注浆压力的关系,以及注浆压力衰减的变化规律,可得劈裂通道宽度的分布方程:

(14)

式中:

A——脉冲扩散半径。

对式(14)分离变量并积分,得到劈裂通道总宽度t在均质砂层内的衰减函数:

(15)

式中:

K0——待定常数。

由边界条件c=cmax(cmax为浆脉尖端与注浆孔心的距离),t=0可得:

(16)

将K0代入式(15),整理可得砂层劈裂通道宽度分布方程:

(17)

联立式(13)、式(17),考虑劈裂扩展的时空效应,浆液压力分布方程为:

(18)

2 砂土劈裂扩散规律分析

重庆地铁10号线(以下简称“10号线”)某暗挖区间地质状况复杂,开挖揭露地层为典型的中粗砂-粉土夹层,现场采用普通硅酸盐水泥浆液对局部薄弱区域进行加固治理。以实际工程项目为依托,对砂土劈裂注浆机理进行分析。浆液的基本性能参数为:水灰质量比为0.7∶1.0,ηg为12.4×10-3Pas。注浆工艺参数如下:λ为55.8 L/min,注浆压力为2.4～2.6 MPa,注浆管半径为0.05 m。砂土的物理力学性能参数见表1。

表1 砂土物理力学性能参数

2.1 不同注浆压力下浆液扩散半径分析

图5为浆液扩散半径-注浆压力差关系曲线。由图5可知:

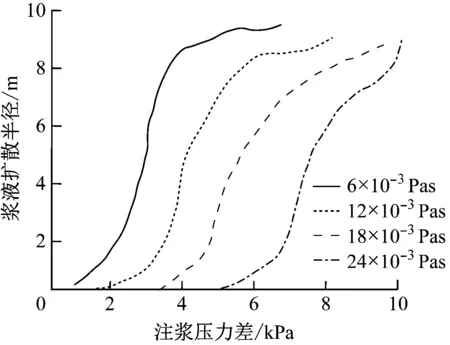
a) 不同浆液黏度时

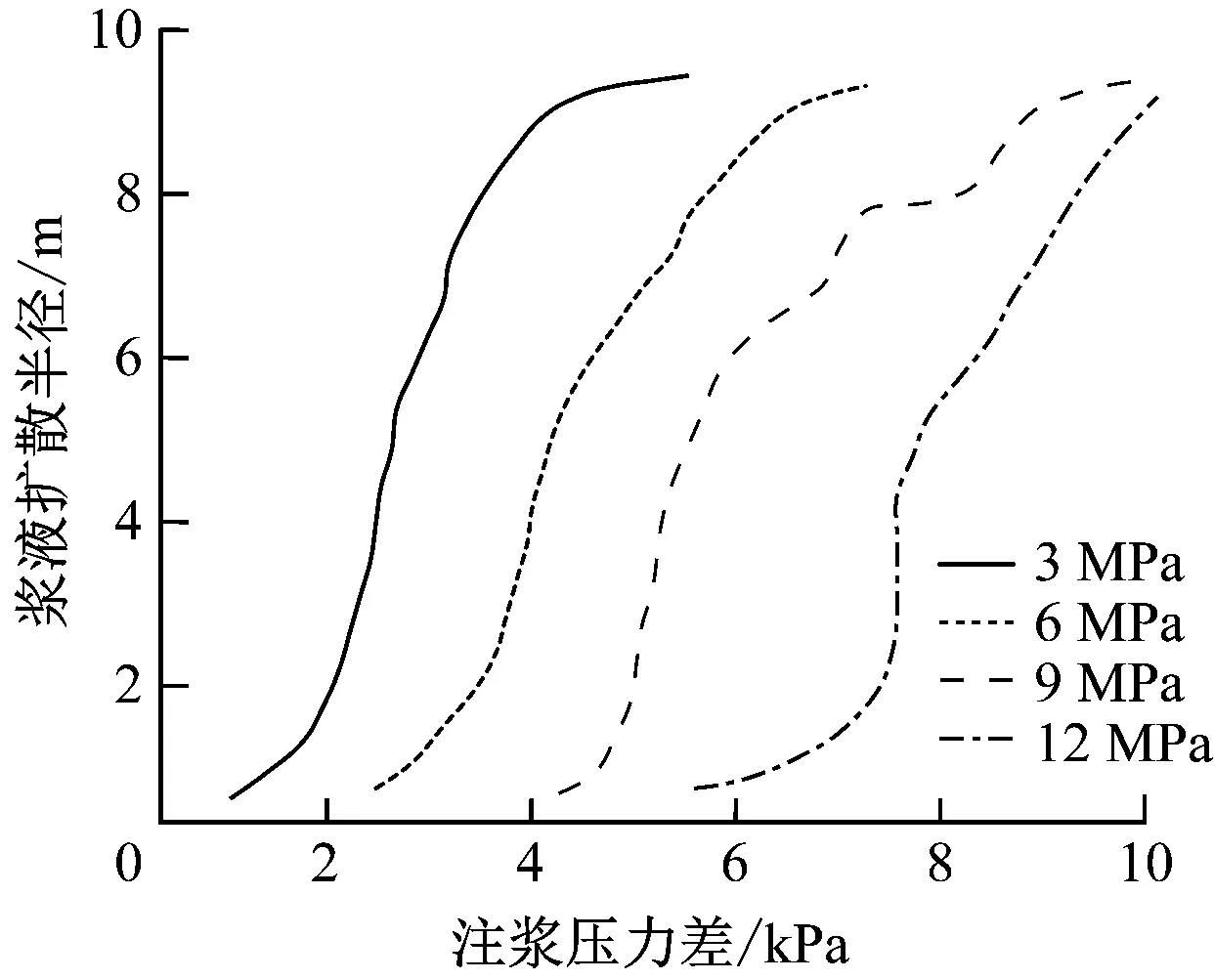
b) 不同砂土压缩模量时

1) 注浆压力在较低水平时,浆液劈裂扩散范围十分有限,砂土地基改良加固的效果不明显。当注浆压力超过临界值后,浆液扩散半径剧烈增长,与注浆压力差呈高幂次函数关系。

2) 浆液黏度、砂土弹性模量等参数,对劈裂注浆效果影响非常显著。浆液黏度越小,浆液劈裂扩散过程中遭遇的黏滞阻力越小,浆液扩散半径越大;砂土弹性模量越小,浆液劈裂过程中经受的土体阻抗越小,扩散半径同样越大。

3) 在实际工程中,受砂土结构的自然性、施工工艺的多样性,以及浆液扩散规律的复杂性影响,注浆扩散范围比理论计算值要小很多。

2.2 劈裂通道宽度衰减规律

图6为劈裂通道宽度-浆液扩散距离关系曲线。由图6可知:

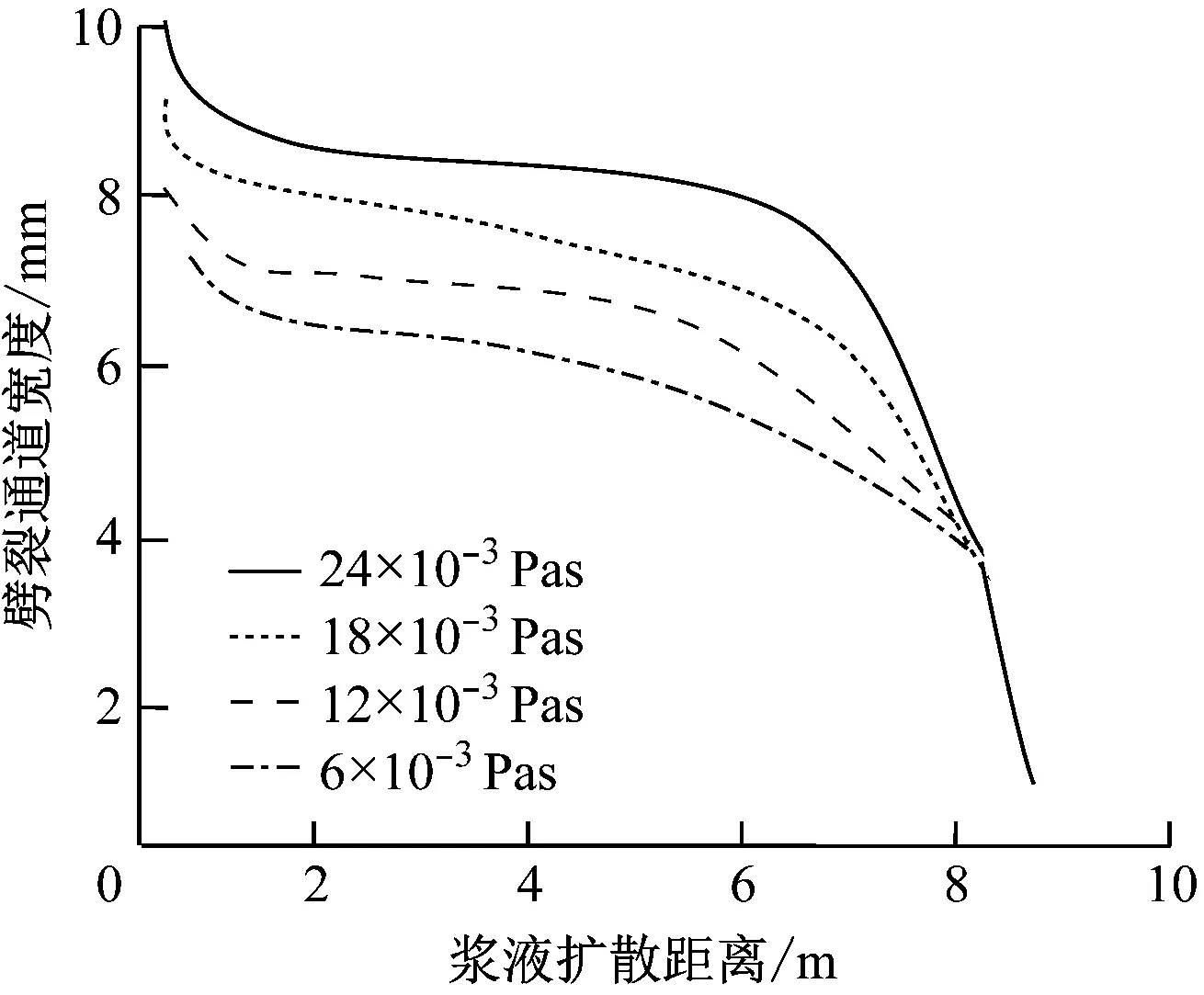
a) 不同浆液黏度时

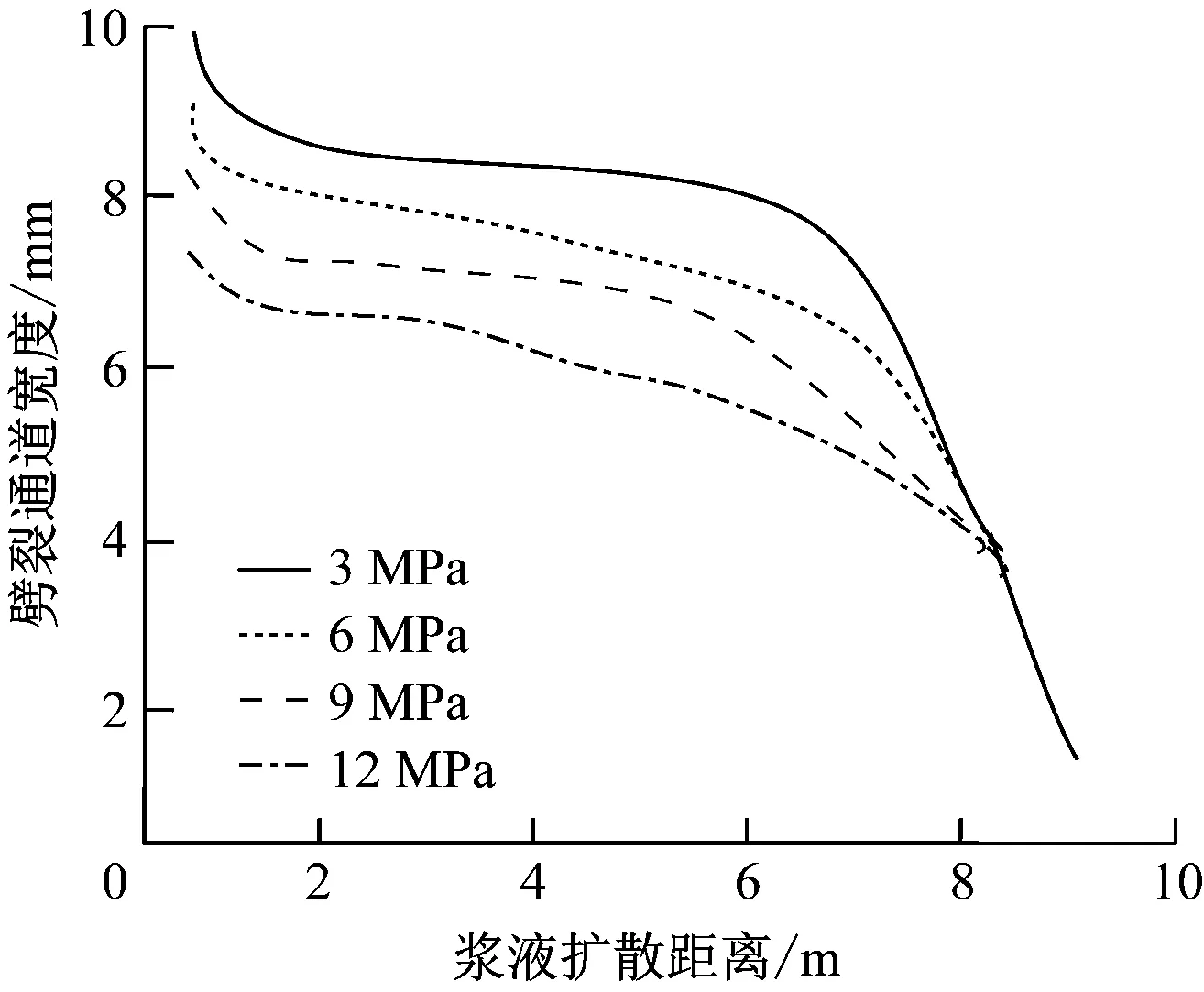
b) 不同砂土压缩模量时

1) 孔口附近浆脉宽度最大,约为10 mm,且浆液扩散距离沿扩散路径浆脉宽度逐渐衰减,至浆液锋面为 0。中间浆液扩散区段浆脉宽度衰减趋势较为平缓,而初始和终端浆脉宽度衰减较为剧烈,此变化规律与注浆压力的变化规律基本一致。

2) 浆液性能、地质参数对劈裂扩散过程存在显著影响,劈裂通道宽度随浆液黏度增加而增加,随砂土弹性模量增加而减小。

3 工程实测

10号线二期兰花路站—后堡站区间为中粗砂-粉土地层,盾构掘进中经受了涌水、拱壁坍塌等多种事故。现场采用普通硅酸盐水泥浆液,对长度为2 km的区间进行了加固治理。依据稀浆开灌、逐级变浓的原则,现场共灌注水泥材料12.1 t。注浆压力控制在2.4～2.6 MPa,注浆孔间距为2.8～3.2 m。注浆结束后发现砂层中存在丰富的结石浆脉,主浆脉长度为63～74 cm,次浆脉长度为16～22 cm。

根据本文分析推导的浆土耦合效应下砂土劈裂注浆的基本规律,结合郑州地区的施工经验,通过式(14)、式(17),得到主浆脉长度为73～80 cm,次浆脉长度为14～18 cm。经与现场开挖所检测的浆脉长度相比,其理论计算值偏大17%～22%左右,计算误差处于工程设计允许范围内。

浆脉长度开挖检测值与理论计算值存在 17%～22%误差,究其原因是:

1) 砂土存在原生结构性,局部不良地质区域经过注浆后,其结构形态、力学强度及刚度显著改变和提升,浆液劈裂扩展需要更高的压力,而理论计算中仍采用均质各向同性假定。

2) 浆液压力衰减是由砂土侧壁的摩阻、黏性流体的黏滞性等多因素造成的,理论计算中忽略了砂土压缩变形对浆液扩散的影响。

4 结论

1) 浆液压力在注浆起始和末尾阶段变化较为剧烈,而在中间阶段变化稳定。劈裂通道宽度基本由注浆压力决定。

2) 工程验证发现,浆脉长度开挖检测值与理论计算值存在17%～22%的误差,表明该理论模型具有一定的工程应用价值,对指导实际注浆设计、施工具有参考意义。

3) 水灰比是影响砂土加固强度的重要因素。为了提高注浆加固效果,工程中有时会使用较高浓度的水泥浆液。水灰质量比为0.5∶1.0～0.6∶1.0的水泥浆液属于幂律流体,其流动扩散规律与宾汉型浆液不同,下一步可针对幂律流体扩散特性,对劈裂注浆机理展开分析。

4) 由于地质条件的天然复杂性和自然结构性,砂层内分布有不规则的孔隙和空洞。均匀各向同性弹性介质的假设在理论计算中节省了一定工作量,但与实际工程情况差别仍然较大。

5) 注浆施工作业不可避免地受天然重力场和超固结应力场的影响,本文研究工作忽略了这种影响,有待进一步深入研究。