一种快速的空时二维谱估计算法

2024-03-27管亮中张志强

舰船电子对抗 2024年1期

管亮中,曾杰,张志强,贾佳

(1.空军工程大学,河南信阳 464000;2.解放军95865部队,河南信阳 464000;3.解放军95606部队,北京 100011)

0 引言

谱估计技术以其优异的参数估计能力在雷达、通信、电子战等领域均得到广泛的应用。谱估计技术最初应用在一维参数估计上,通过分析其基本原理可知,这种技术较易推广到多维参数估计,多维参数估计的应用场景也更具普适性。文献[1]针对传统空时自适应算法对不同来向的干扰抑制问题展开研究,提出了改进的空时处理器结构,有效抑制了窄带和宽带干扰,提高输出信干噪比,改善了系统性能。文献[2]针对阵元间距较大时容易使得空时二维频率、到达角估计模糊问题,采用由非均匀时延间隔的延迟器组成的虚拟阵列估计信号频率和到达角,突破了时域和空域采样定理的限制。文献[3]将多级维纳滤波器引入到空时级联频率-到达角估计中,提出了一种快速级联估计算法。本文在文献[3]的基础上,将多级维纳滤波器引入到空时二维MUSIC算法中,提出了一种快速的空时二维谱估计快速算法。快速算法通过正交变换、乘加运算得到噪声子空间,减少了算法运算量。仿真结果表明：在同等条件下,快速算法与原有算法性能相当。

1 空时二维谱估计原理

1.1 信号模型

参照文献[3]给出的信号模型,以均匀线阵为例,阵元数为M,阵元间距为d,每个阵元抽头数为K,相邻延时间隔为τ,快拍数为N,以阵元1为基准点。

假设有Q个窄带远场信号辐射到线阵,彼此相互独立,可将复包络表示为s1(t),s2(t),…,sQ(t)。在t时刻,第m个阵元上第k个抽头延迟的输出为：

(1)

式中：m=1,2,…M;k=1,2,…,K;c为光速;nm(t)是第m个阵元的高斯白噪声,彼此相互独立,均值为零,方差为σ2,与信号源不相关。

可得第m个阵元t时刻的数据矢量为Xm(t)=AmS(t)+Nm(t),进一步将Xm(t)组合为X(t)=AS(t)+N(t)。

1.2 空时二维MUSIC算法原理[4]

在N次快拍下,空时阵列输出协方差矩阵为：

R=E[XXH]=AE[SSH]AH+σ2I=

ARSAH+σ2I

(2)

运用经典算法,可对式(2)进行特征根分解,得到：

(3)

利用矩阵A与噪声子空间的正交性,构造空时二维MUSIC谱函数：

(4)

根据经典MUSIC算法原理可知,在使用数据足够长或信噪比适当的情况下,二维MUSIC算法可以得到任意精度的估计值。

2 多级维纳滤波器

考虑非奇异矩阵T1=[h1B1],其中h1为单位化的互相关矢量,B1是一个MK×(MK-1)维的矩阵,它张成rx0d0的零空间。可用T1对观测数据X0(k)进行变换,再进行滤波,进而产生一个新的(MK-1)维的维纳滤波器,该滤波器与典型维纳滤波器结构相同。因此,维纳滤波器ω2可用相同的方法进行分解,直到最后形成的维纳滤波器只有一维。图1给出了N=4时维纳滤波器正交投影分解后的结构。

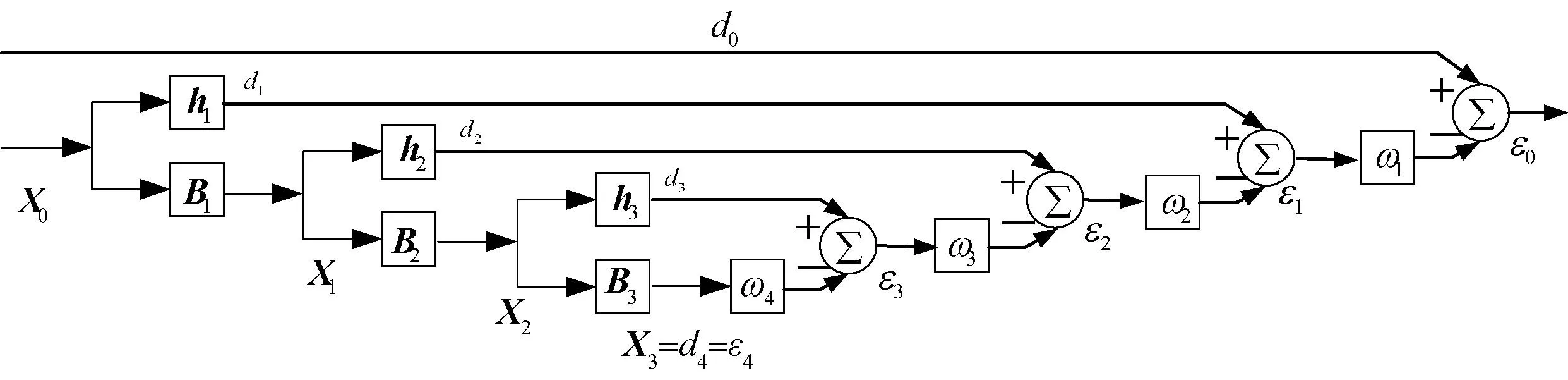
图1 N =4时多级维纳滤波器结构

3 快速二维MUSIC算法

如果已知信号结构,可以使用先验信息来构造参考信号d0(k),再将第2节的算法应用至多级维纳滤波器中,即可完成信号的二维参数估计。可以取d0(k)为信号源中的一个,其结果与基于特征分解的MUSIC算法结果是相同的。但实际一般没有信号结构这一先验信息,为了解决此类问题,可采用图2所示MSWF预处理模型经典模型[6-8]。其中X为MK×N维的虚拟阵列采样数据构成的矩阵,每一列代表1次快拍。取B0为求输入自相关,取h0为求自相关的第1列,即：d0=Rxx(1,：),X0=Rxx。

图2 应用MSWF预处理模型

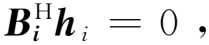
(5)

文中所提快速算法具体步骤如下：

(1) 预处理：d0=Rxx(1,：),X0=Rxx;

(2) 前向递推：

(6)

式中：i=1,2,…,MK。

4 算法运算量讨论

采用相关相减结构,求得噪声子空间的运算量为o[(N+2P)M2K2+2PMK],而采用特征根分解得到噪声子空间的运算量为o(NM2K2+M3K3)。文中所提快速算法在求解噪声子空间时,采用乘加运算代替了特征根分解,从一定程度上减少了运算量,更加便于硬件实现。图3给出了信源数为3、快拍数为128、延迟数为4条件下的运算量随阵元个数变化的关系。仿真结果表明：随着阵元个数的增加,文中所提快速算法的运算量减少越明显。