舰载跟踪雷达对掠海飞行目标的跟踪影响分析

刘应盼,柏 磊,陈 峰,罗宇轩

(中国船舶集团有限公司第七二三研究所,江苏 扬州 225101)

0 引 言

跟踪雷达的使命任务是能够快速捕获并有效跟踪目标,实时精确测量目标的位置信息,并将目标的定位数据及误差数据送给火控系统,以便于火控系统对目标实施精确打击,因此对跟踪雷达的精度往往有着极高的要求。

雷达对掠海小目标实施跟踪时,容易受到复杂海情的影响,一方面由于多路径效应导致雷达的回波是探测目标的直接路径回波与反射路径回波的叠加,该回波的幅度和相位信息随着目标高度和距离发生周期性变化,造成多路径误差,影响跟踪雷达精度;另一方面由于雷达通过电磁波传播来获取目标的位置信息,而大气环境参数的不均匀性使雷达探测目标时产生大气折射误差,因此高精度雷达测量系统一般都会对大气折射误差进行修正。

在大气边界层尤其是在近地层中传播的电磁波,由于受大气折射的影响,其传播轨迹会发生弯曲。当电波射线的曲率超过地球表面曲率时,电磁波会部分地被陷获在一定厚度的大气层结内,这种大气层结称为大气波导[1]。根据大气折射指数垂直梯度的大小不同,可以将大气折射分为负折射、正常折射、临界折射、超折射等。其传播示意图如图1所示。

图1 大气折射传播示意图

基于常规大气条件下成熟的大气折射修正技术,现役装备均已应用相关修正技术,并取得了良好的效果。由于大气波导是一种极端的超折射现象,雷达仰角测量误差相对正常折射要更大[2],这对于高精度跟踪雷达是无法接受的。大气波导存在条件下,通常的折射修正模型已不再适用,因此对大气波导引起的折射误差进行分析研究很有必要。

1 现象分析

在某次跟踪雷达对掠海飞行目标的跟踪试验任务后,对雷达测量值与真值处理时发现,仰角系统误差在远距离均出现明显偏大的现象,数量级大概在2～3 mrad之间,仰角误差曲线如图2所示。

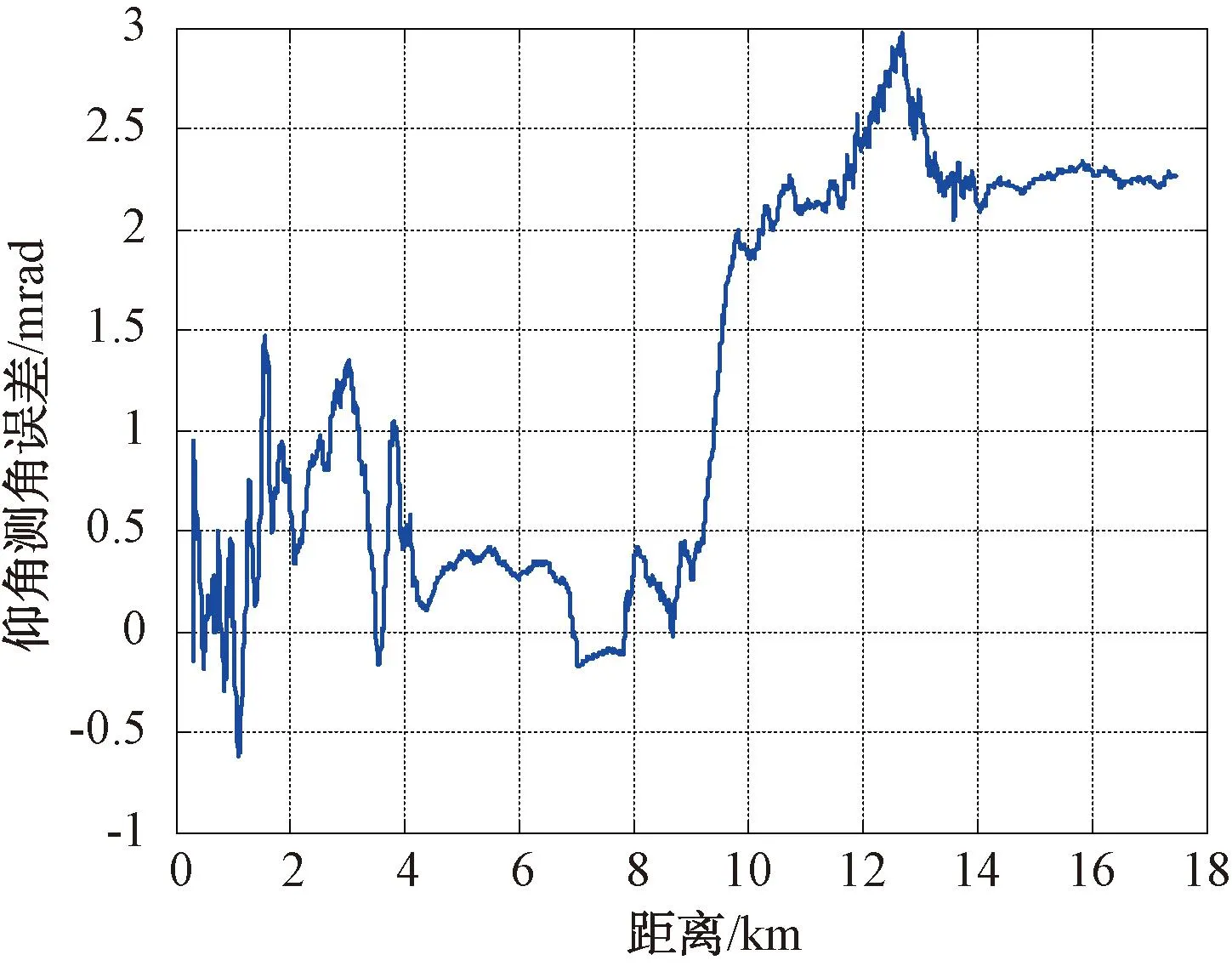
图2 仰角误差曲线图

远距离误差偏大问题和精度分析紧密相关,因此对影响雷达精度的一切因素进行考虑,同时结合掠海航路的特点和电磁波传播影响,综合一切可能导致该问题的原因。建立了图3所示的问题定位流程图。

图3 仰角远距离误差偏大分析流程示意图

(1) 仰角系统误差标校不准确

仰角系统误差标校不准确不会导致图2的误差分布,从整个跟踪数据区段来看,如果出现仰角系统误差标校不准确的情况,则从捷径至18 km整个误差曲线应有固定偏置,如图4所示。而实际误差曲线在10 km以内,系统差在0.4 mrad左右;10 km以外,则在2 mrad左右。

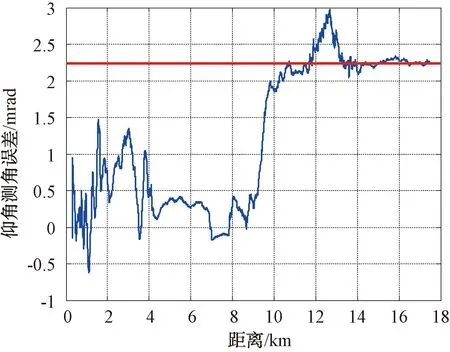
图4 仰角误差分布示意图

(2) 多路径引起误差

雷达在海洋环境下进行低空目标跟踪时,受多路径影响尤为显著。多路径效应与目标高度、目标距离、雷达架设高度、雷达工作频率、雷达的波束宽度、海面反射系数、雷达电磁波极化方式等因素均有关系。对于舰载跟踪雷达,多路径效应的影响是雷达在设计跟踪掠海飞行目标功能时需重点解决的问题。

对天线架高16 m,目标高度5 m,使用频率捷变,进行测角误差仿真,得出如图5所示的结果。

图5 按照试验条件时理论仿真曲线

根据图5矩形区域可知,在试验目标高度和架高情况下,在10 km以外,只存在多路径影响的情况下不会出现仰角远距离持续偏大2 mrad的情况,而10 km以内多路径误差是周期性变化,符合多路径误差变化规律,且仿真的仰角误差和试验实测曲线较吻合。

由上述分析可得,远距离仰角误差大是由于多路径引起的测角误差原因不成立,近距离受多路径影响较大。

(3) 大气波导效应

依据大气修正折射率的大小将大气波导分为3种：表面波导、抬升波导和蒸发波导。蒸发波导多在海洋大气环境中出现,而表面波导和抬升波导多出现在陆地大气环境中[3]。图6给出了这4种类型的大气波导示意图。

图6 大气波导的四种类型示意图

蒸发波导是由于海面水汽蒸发使得在海面上很小高度范围内的大气湿度随高度锐减而形成的(如图6(d)所示)。蒸发波导高度在不同地点、不同时间内均可能发生变化,通常在低纬度海域夏季的白天蒸发波导的高度较高。据不完全统计,蒸发波导的高度范围大概在几米～40 m之间,频率高于3 GHz的雷达设备,发射角在0.8°以下容易受蒸发波导的影响[4]。蒸发波导对雷达探测目标的影响主要包括以下3个方面：

(a) 蒸发波导能将电磁波经过多次折射传送到理论视距外,增加雷达作用距离。

(b) 蒸发波导将电磁波陷获在波导层内,使得雷达探测不到波导层外的目标,形成雷达探测盲区。

(c) 由于蒸发波导折射更严重,因此可引起雷达的测距、测角、测速的误差比常规折射条件所引起的误差要大很多,尤其是对仰角误差更为明显[5]。

根据前述分析,本次试验雷达架高、目标高度均在蒸发波导层内,且雷达频率为X波段,高于3 GHz,雷达发射角小于0.8°,同时试验结果表明远距离仰角误差更大,更符合蒸发波导的产生规律,因此本文远距离仰角误差异常原因从蒸发波导的产生机理展开论证。

2 近距离多路径影响分析

当雷达跟踪掠海飞行目标时,雷达主波束经海面的镜面反射和漫反射而形成镜像反射信号,雷达接收回波为反射波和直射波的矢量合成。由于反射波与直射波的路径差及海面引入的相角,使反射波相对于直射波产生1个相移,矢量合成的结果使角误差信号失真,造成跟踪结果不准确。根据镜像反射信号进入到天线波束的位置大致分为2种：

(1) 在远距离时,镜像进入天线主波束,仰角误差基本上是双反射体目标的闪烁误差,误差计算公式为：

(1)

式中：θd为目标仰角;Δθ是误差,单位与θd相同;Ø为信号的总相移;ρ=|ρ|ejφ为复反射系数。

(2) 在近距离时,镜像信号进入天线副瓣波束,其均方根值可由如下计算公式预测：

(2)

式中：σ是仰角多路径误差的均方根值;θ3 dB为天线波束宽度;ρ为复反射系数;Gse(峰值)为和方向图峰值增益与在镜像信号到达角方向上差方向图副瓣电平功率之比。

设定仿真条件为：雷达工作在X波段频率捷变,雷达重频100 μs,16点快速傅里叶变换(FFT),仿真距离0～10 km,海情2级,天线距海面高度15 m。对目标高度为5 m、10 m、20 m、40 m的目标进行测角误差仿真,如图7所示。

从仿真结果可以看出,仰角误差在不同距离区间内存在较大的起伏波动,多路径引起目标信噪比随目标距离周期性变强或变弱,导致仰角测角误差出现周期性变化,并且变化周期不固定。由于雷达架高变化导致的直射与反射路径间的相位变化,从而使得雷达仰角大误差出现在不同距离上,从仿真结果可以直观看出,不同工作架高下雷达仰角测量误差出现平移。

根据上述分析,10 km以内近距离的仿真分析与图2的实测结果图比较接近,因此近距离的仰角误差变化受多路径影响较大。

3 远距离蒸发波导影响分析

3.1 蒸发波导传播必要性分析

对于蒸发波导传播而言,除了确定存在蒸发波导之外,还需要知道实现蒸发波导传播的电波的临界波长和临界入射角。因此蒸发波导实现的必要条件有以下2点：计算得出蒸发波导的临界波长,只有工作波长小于临界波长时才能进行蒸发波导传播;计算得出蒸发波导的临界入射角,只有电磁波初始发射时的仰角小于临界入射角时,才能进行蒸发波导传播[6]。

(1) 试验大气环境

试验地点在沿海地区,靠近渤海湾,时间为下午2点左右。试验组织前,相关气象测绘部门对当天天气进行了预测,当地气象预报测得试验时海域的天气情况如下：

(a) (120.8E、40.5N)上午相关海域蒸发波导高度5～10 m,下午相关海域蒸发波导高度10～20 m;

(b) 相关海域无悬空波导;

(c) 11时～17时,相关海域附近有大范围表面波导,高度最高为80～150 m。

(2) 波导传播的临界入射角

图8 电磁波形成波导传播的临界入射角示意图

计算θc的经验公式为：

(3)

式中：|Md|为发射源高度处与波导顶高处修正折射率的差值。

根据公式(3)可知,陷获角随着波导强度的增大而不断增大,在大部分波导强度范围内陷获角小于0.8°,雷达波束宽度为2°,当试验时跟踪雷达的仰角<1°～1.8°时,满足陷获角条件。由跟踪数据得知,刚完成捕获跟踪时发射角分别为0.017°、0.032°左右,均满足临界发射角条件。

(3) 波导传播的临界波长

波导传播临界波长要求电磁波能够被大气波导捕获,从而形成大气波导传播的最大波长。由于试验雷达天线极化方式是垂直极化,得出垂直极化时临界波长λV的计算公式为：

(4)

式中：h为蒸发波导高度,单位为m;λV为波长,单位为cm;Md定义为发射源高度处于波导顶部高度修正折射率的差值。

陷获层内大气修正折射指数梯度为-90 M/km 时,雷达位置距离海面16 m,当蒸发波导高度为20 m时,根据公式(2)得出截止波长大概为9 cm,跟踪雷达的中心频率波长为3 cm,其值<9 cm,满足大气波导的截止波长要求。

3.2 蒸发波导不同发射角的仰角定位误差

蒸发波导的电磁波射线轨迹可以用球面分层模型进行描述,设地球半径为r,大气分为n层,当n做够大时,层内的大气折射指数可看作近似相等,层之间的大气折射指数随着高度增加而减小。假设电磁波传播初始位置位于A点,距离地面高度为h0,电磁波初始仰角为θ0。电磁波传播射线上的任意一点Ai位置可表示为[hi,αi],其中,hi为射线任一点的离地高度,αi为任一点偏离初始位置的地心张角(∠AOAi),电磁波折射时的射线轨迹图和几何模型示意图如图9和图10所示。

图10 电磁波折射几何模型图

根据图10可知,蒸发波导中雷达的仰角误差可由雷达探测的视在仰角(即为θ0)与雷达天线中心到目标的真实仰角β0差值求得。假设目标在射线的任一位置Ai,则真实仰角根据图10几何关系求得β0为：

(5)

则仰角误差为：

Δ=θ0-β0

(6)

设置仿真条件,蒸发波导高度20 m,雷达天线高度10 m,由于试验时,雷达捕获跟踪上目标时发射角在0.016°左右,故仿真时增加发射角0.016°的仿真。雷达发射角分别以0.2°、0.1°、0.016°、-0.15°、-0.25°发射跟踪目标,电磁波按照图9进行传播和公式(5)、公式(6)进行计算时,仿真得出不同发射角时的仰角定位误差,如表1所示。

表1 不同发射角时雷达仰角定位误差

3.3 试验射线传播路径反演及实测数据误差分析

根据试验仰角误差结果推算,并结合蒸发波导射线传输规律,对试验跟踪时发射射线的轨迹进行推算,绘制的射线传播路径如图11所示。

图11 试验时跟踪雷达电磁波传播示意图

图11中,实线代表目标在远距离处,雷达发射的电磁波需要经过一次陷获折射后,经过海面反射照射到目标,此时经过很长一段时间一直到9.2 km临界处,均是这种反射一次后到达目标路径。从17 km～9.2 km,此时天线仰角测量值一直在0.3 mrad左右缓慢变化,而目标仰角实际值随距离从17 km～9.2 km在-1.9 mrad处,因此在17 km～9.2 km一直偏置2.2 mrad左右的系统差。到9.2 km后,第一次反射的零点在目标后,不需要经过海面反射到达目标,此时雷达视在仰角与真实目标仰角之差很小。和仰角误差结果表现一致。仰角测量值和真值曲线如图12所示。

图12 仰角测量值和真值曲线

4 结束语

自由空间中,雷达探测目标时,电磁波传播是沿直线传播的,此时雷达对目标的参数测量受环境影响很小,而在实际的大气环境中,电磁波容易受到温度、湿度、大气压力等大气环境因素影响,导致电磁波传播轨迹发生弯曲,蒸发波导使得电波射线弯曲的曲率超过地球曲率,陷获在一定的大气层结构中,此时电磁波传播需经过多次折射后到达目标。

本文从远距离仰角误差偏大的试验现象出发,对此现象进行深入分析,定位得出：近距离时误差表现受多路径影响较大,远距离误差偏大是由于海面蒸发波导的影响导致的。对近距离和远距离仰角误差影响2个方面进行分析论证,并对试验时蒸发波导产生的必要条件进行分析,进一步证明了试验由于蒸发波导的存在导致此现象的发生;仿真得出了在蒸发波导条件下雷达探测误差的计算模型,给出不同发射角时雷达仰角定位误差与探测距离的关系;文章最后利用蒸发波导的机理对实测数据进行了误差分析,分析后得出实测数据与理论分析一致。本文的研究内容为雷达探测掠海目标精度考核异常提供了定位思路,同时也为后续能找到修正大气波导影响的方法提供了理论研究基础,具有良好的应用价值。