Floyd多源最短路径算法的并行化研究

龚宁静

（湖北警官学院信息技术系，武汉 430034）

0 引言

人们经常在计算机中使用图结构来分析和处理实际生活中那些有多对多映射关系的数据。图结构中若顶点A经过某些边或弧可以到达顶点B，那么由权值之和最小的边或弧组成的路径就是顶点A到顶点B的最短路径。我们经常使用最短路径算法来解决实际生活中遇到的很多问题，比如：地图导航、物流管理、交通控制、通信网络、社交网络，等等。

图的最短路径问题又分为单源最短路径和多源最短路径两种应用场景。单源最短路径是以图结构中某一顶点为源点，求从源点出发到图中其它所有顶点的最短路径。多源最短路径是求解图结构中任意两个顶点之间的最短路径［1］。以地图导航为例：假如导航APP 只为一个用户服务，且用户以家作为源点。那么导航可以使用单源最短路径算法为此用户计算出从他家到其它任何目的地的最短路线。但实际上导航APP 面对的用户成千上万，因此APP 最终是使用多源最短路径算法同时为所有向它请求的用户给出导航服务。Floyd 多源最短路径算法最大的缺点是执行效率低，时间复杂度为O（n3）。因此当图结构中顶点、边或弧的数量较多时，计算时间会大幅度增加，难以满足实时响应的需求［2-4］。针对Floyd 算法的这一缺点，本文从并行计算的角度来找出该算法的优化办法，降低时间复杂度，提高执行效率［5-6］。

1 Floyd多源最短路径的现有算法

Floyd 算法求解图结构中任意两个顶点之间的最短路径。假设有一个图结构如图1 所示（图中包含5 个顶点、9 条弧，每条弧的权值为标在该弧旁边的数字）。

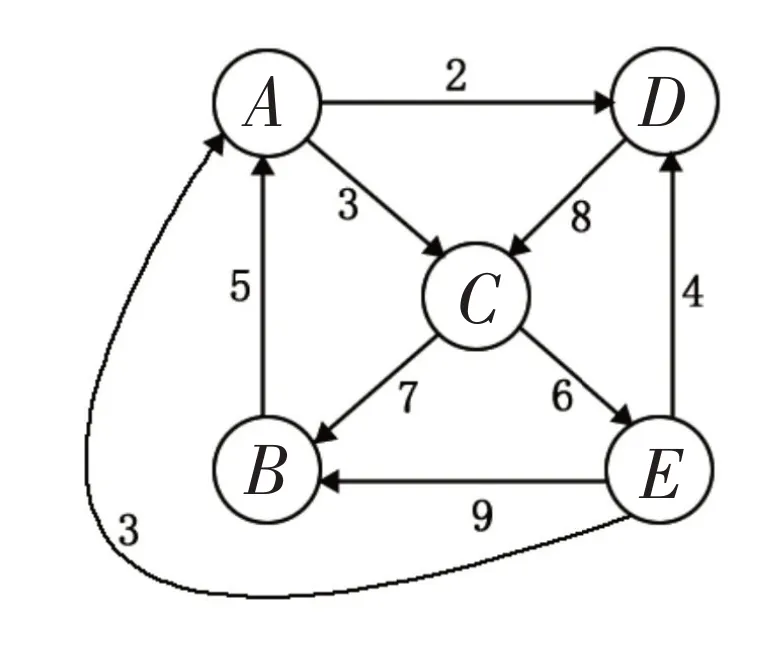
图1 待求多源最短路径的图结构

如果要对该图结构求解多源最短路径，设图中顶点数为n，那么每个顶点都能求出n-1 条最短路径，图中一共可以求出n（n-1）条最短路径。我们可以把所有的最短路径存储在一个n行n列的矩阵中，如图2所示。图2中一共n2个矩阵元素，除去主对角线元素外，剩下的n（n-1）个元素刚好可以存储和对应每一条最短路径。比如矩阵中B行D列（1 行3 列）的元素对应的就是顶点B到顶点D的最短路径。

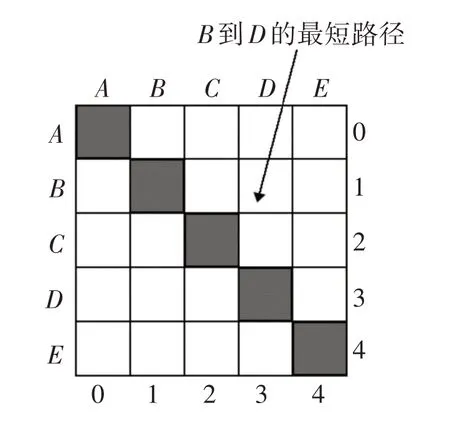
图2 存储所有最短路径的矩阵

Floyd 算法求所有最短路径其实是利用动态规划同时寻找给定加权图中任意两顶点之间的最短路径。对于每一对顶点的最短路径的寻找，使用插点法来逐个比较可选路径，通过保留较小者、淘汰较大者来刷新当前最短路径。可选路径通过枚举插入的不同顶点来生成。假设矩阵用二维数组D来实现，那么顶点i 到顶点j 的最短路径在寻找过程中的一次比较和刷新算法如下：

算法1：当插入顶点为u时，i到j最短路径的更新

Floyd 算法会同时对所有最短路径进行比较和刷新，因此当枚举的插入点为顶点u时，其它最短路径也会比较自己的当前最短路径和插入了顶点u后的路径哪个更短，用更短的值来作为最新的当前最短路径。这部分的完整代码如下：

算法2：当插入顶点为u时，矩阵D的一次迭代

以上代码通过枚举插入顶点u，对保存在矩阵中的所有最短路径都进行了一次比较和刷新。我们可以把这一部分代码看成是矩阵D的一次迭代计算。代码块的时间复杂度为O（n2）。为了无遗漏地找出所有的可选路径加以比较，图中所有的顶点都需要被枚举成插入点。因此还需要在上面代码块的外层再套一个循环来实现将图中所有顶点枚举成插入点。初始状态下矩阵D其实就是该图结构的邻接矩阵。完整算法的时间复杂度为O（n3）。Floyd 关于矩阵D的核心算法如下：

算法3：Floyd关于矩阵D的计算

Floyd 现有算法的时间复杂度太高，用该算法来处理现实中的实际问题时，对应的图结构往往是顶点和弧的数量巨大的稠密图。在数据量大的情况下，算法的执行效率会显著降低，难以保证响应的时间。许多实际应用在这种情况下会放弃Floyd算法使用其它算法来替代［7］。

2 一次矩阵迭代的并行计算实现

能不能找到办法降低Floyd 算法的时间复杂度从而提高执行效率呢？在分析Floyd 算法的代码时，我们发现算法2 描述的当插入的顶点为u时，整个矩阵D的一次迭代计算其实是按照先后顺序一条一条更新了所有最短路径。因此矩阵D的一次迭代执行了n2次循环操作，每次循环只修改了矩阵中一个元素，其它元素处于等待状态。其它元素能不能不等待，也同步执行更新呢？在矩阵D的一次迭代中，每一条最短路径的更新都只会比较自己现有的最短路径和插入顶点u生成的路径哪条更短？计算过程不依赖其它路径的更新。因此矩阵D中每个矩阵元素的更新都是可以同步进行的。

有了以上的分析，我们可以通过并行计算的角度来重写算法2 的代码，将矩阵D的一次迭代用矩阵的运算方式实现处理，在一次运算的时间内将矩阵中所有元素同步更新到位。

为了能顺利地进行矩阵点运算，也就是两个矩阵中对应位置元素的运算，首先要根据矩阵D进行一些变化，生成帮助运算的辅助矩阵。算法2 中每一条最短路径D［i］［j］都要与插入顶点u后生成的路径D［i］［u］+D［u］［j］比较大小。在对整个矩阵D更新时，i和j的取值范围是从0到n-1，而u的取值固定不变。因此，我们要构造一个矩阵D,D'中每个元素D'［i］［j］的值等于D矩阵中对应的D［i］［u］+D［u］［j］的值。又因为D'［i］［j］是通过D［i］［u］+D［u］［j］得到的，所以我们先构造两个矩阵Dr和Dc，使Dr和Dc相加能得到D'。Dr中每i行的元素都应该是D矩阵中的D［i］［u］，Dc中每j列的元素都应该是D矩阵中的D［u］［j］。假设插入顶点u为第0个顶点，那么矩阵Dr可以取矩阵D的第0 列并平铺成5列得到。矩阵Dc可以取矩阵D的第0 行并平铺成5行得到。

通过图3 我们可以看到，通过矩阵D得到的Dr和Dc中每个元素均来自矩阵D。

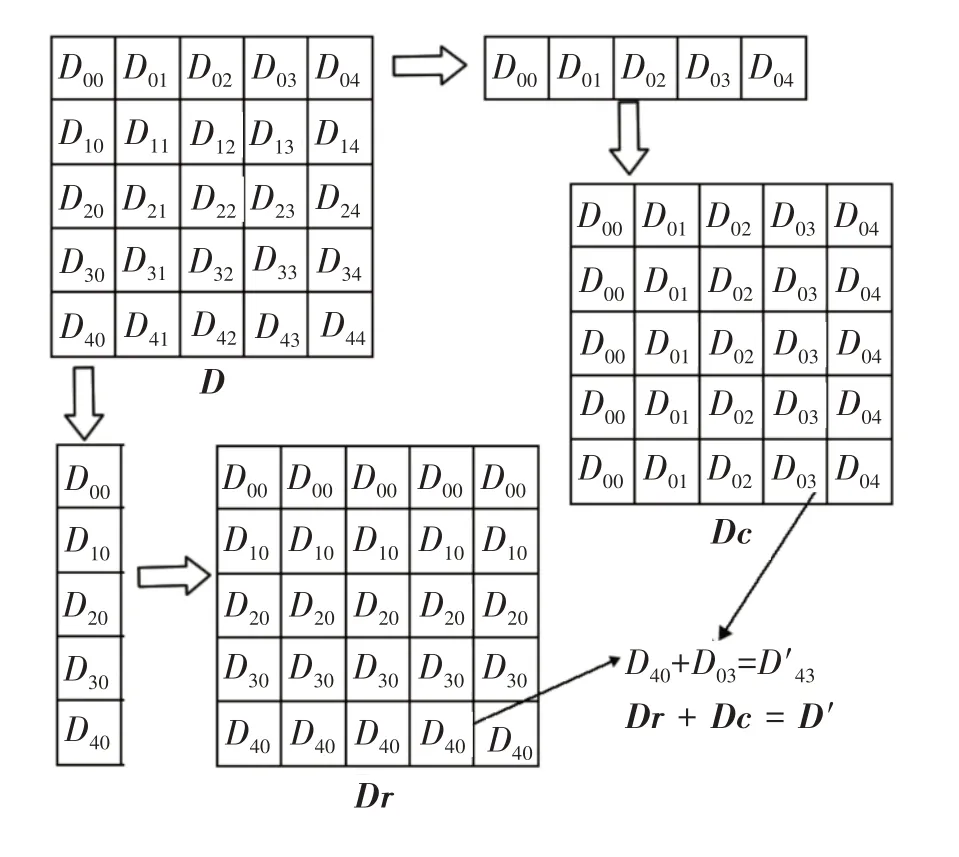
图3 构造矩阵D'的矩阵Dr和Dc

矩阵Dr和Dc中的任意元素Dij表示该元素来自矩阵D的第i行第j列，是矩阵D中D［i］［j］。所以当Dr和Dc进行矩阵相加时，对应位置的元素直接做加法。比如Dr中第4 行第3 列的元素D40与Dc中第4行第3列的元素D03位置对应，这两个元素的值相加其实就是矩阵D中的D［4］［0］+D［0］［3］，相加的结果就是顶点4 到顶点3 在插入了顶点0 后生成的路径。如果我们用矩阵D'来保存Dr和Dc相加的结果，按照矩阵加法的规则，刚才两个元素相加的结果会被保存在结果矩阵的第4 行第3 列，也就是矩阵D'的D'［4］［3］中。由此，我们构造出了矩阵D',D'中每个元素D'［i］［j］的值等于D矩阵中对应的D［i］［0］+D［0］［j］的值。

根据以上分析，我们可以从并行计算的角度重写算法2，形成算法4。由于这里描述的是基于并行计算的步骤，而MATLAB 和Python 编程环境下可以很方便地进行并行处理，因此该算法使用MATLAB 的编程语法来进行描述。将之前的算法2 和基于并行计算的算法4 相比较，这两个算法都是实现矩阵D的一次迭代，在插入点为顶点u时对矩阵中所有元素（矩阵中保存的所有当前最短路径）进行比较和刷新。算法2的时间复杂度为O（n2），而算法4 的时间复杂度为O（1）。通过对Floyd 中一次矩阵迭代的并行计算实现，算法4 大大降低了这一步骤的时间复杂度，从平方阶直接降到了常数阶。

算法4：当插入顶点为u时，一次矩阵迭代的并行计算

3 Floyd算法的并行计算实现

接下来，我们通过算法5 给出Floyd 算法中关于矩阵D的并行计算的核心算法。和算法4一样，这里使用MATLAB 编程语法来描述该算法。初始状态时，矩阵D是待求多源最短路径的图结构对应的邻接矩阵。u的初始取值为1，表示首次枚举出的插入点是顶点1。通过D（u，:）取出矩阵D中的第u行，再通过repmat（ ，n，1）将这一行平铺n行，得到矩阵Dc。通过D（：，u）取出矩阵D中的第u列，再通过repmat（ ，1，n）将这一列平铺n列，得到矩阵Dr。通过Dr+Dc得到D'，用来保存每一条当前最短路径的出发顶点和目的顶点间如果插入了顶点u后生成的路径长度。通过D= min(D,Dr+Dc)比较D和D'中对应位置的两个元素（两条拥有相同出发顶点和目的顶点的路径）的值，用较短的路径来刷新每一个元素表示的当前最短路径。因此一次循环结束后，矩阵D保存的所有最短路径刷新一遍。下一次循环u的值加1，枚举下一个顶点作为插入点，再来对矩阵D进行下一次整体刷新。当u取值从1 到n全部枚举完毕后，矩阵D的最后状态保存的就是要求出的n（n-1）条最短路径的路径长度。这里算法只关注了最短路径长度矩阵D的处理，省略了对最短路径经过情况矩阵的处理。

算法5：Floyd 算法关于矩阵D的完整并行计算

Floyd 算法经过并行计算的重写后，整体的时间复杂度由原来的O（n3）降低到O（n）。效率得到了大幅度的提升。

4 结语

本文针对现有的Floyd 多源最短路径算法执行效率低下，无法在数据量大的稠密图上高效运行这一问题，从并行计算的角度着手研究，将算法中插入点给定时进行一次矩阵迭代并逐条刷新所有当前最短路径的顺序过程优化为基于并行计算的同步刷新过程。该优化使得Floyd算法的时间复杂度由原来的立方阶降低为线性阶，从理论上提高了算法的执行效率。当然该研究并不完善，后续将会把记录最短路径经过情况的矩阵也纳入进来，进行进一步优化。