基于数学建模能力培养的高职数学教学策略

顾荣

摘要：在教学改革不断深化的背景下，各种新教育理念和方法不断涌现，数学建模能力作为数学学科的重要组成部分，如何渗入教学的各个环节，成为高职数学教师当前主要的研究趋向。基于此，文章通过设计试卷测试学生数学建模能力，并结合相关结果分析学生数学建模能力，阐述基础知识、问题理解能力等影响因素，并从教学内容设计、教学理念方面入手，提出相应的优化对策，为提高学生数学建模能力提供参考。

关键词：数学建模能力；高职；数学教学

在高职数学教学中，部分教师受传统教学理念、方法的影响，在实际教学中不重视数学应用的广泛性，采取的教学策略依然是传统重理论和结果，轻视实践应用能力培养与学习过程的模式，导致设计的教学内容与学生的实际生活距离较远，学生缺乏利用所学知识解决实际问题的能力，明显违背当前新课程改革关于培养学生学科核心素养的要求。为充分落实新课程改革要求，高职数学教学过程应凸显自身特色，重视培养符合新时期要求的应用型人才。为此，教师应充分利用数学建模思维，积极培养学生的数学建模能力，并在此基础上实现提高教学效率、培养学生数学核心素养、培养高素质应用型人才的目标。

一、数学建模内涵

在现有研究成果中，不同学者对数学建模内涵的定义研究切入点不同，所得结果也有显著差异，如学者孙平利在研究中提出，数学建模即学生能够运用所学知识建立假设或近似值来简化一个复杂的情境，并且可以认识到这些假设和近似值可能需要不断地修订。而我国《普通高中数学课程标准》中将数学建模定义为将实际问题进行数学抽象，用语言表达问题，用数学方法建立模型并解决问题。可见，学生必须从现实出发，利用多种分析将复杂问题简单化，并对其中的参数和变量进行深入分析与明确，之后再根据实验观察数据，探讨变量和参数间的联系。学生将得到的关系结果与数学模型相结合，主动进行计算，将得到的结果与现实问题进行比较，验证模型的科学性和合理性，并在此基础上，持续地对模型进行修正和完善，最终运用数学模型解决各类现实问题。

二、学生数学建模能力调查

（一）调查对象

本次研究为探究基于数学建模能力的高职数学教学策略，所以需要对当前学生数学建模能力进行调查。本次研究将通过测试方式，对某职业院校2020级选修数学建模课程的学生进行调查，调查人数共79人，相较于同届其他仅学习必修课程的学生而言，他们接触数学建模的机会更多。

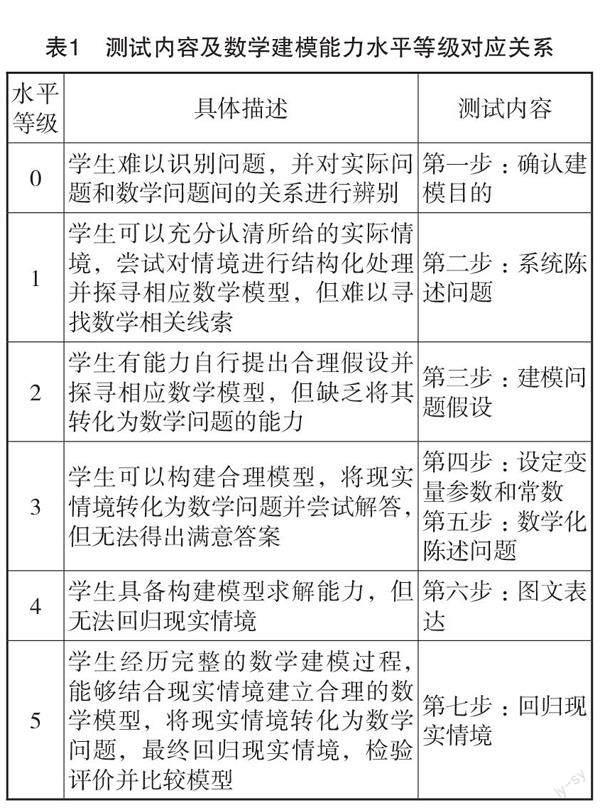
本次测试内容设计主要基于徐斌艳的数学建模能力水平划分标准（等级划分标准为0至5级），通过具体问题情境解决过程，检验6个数学建模能力等级水平，具体等级分级与建模步骤如表1所示。

本次测试共设置涵盖文字题、式子题、图像题在内的18道单项选择题目，题目满分设定为36分，各题打分范围在0～2分区间内，答案不唯一，选择最贴切、最关键得分为2分，其次为1分，无关联或完全没必要不得分。分值大小直接反映学生的数学建模水平。

（二）测试结果统计分析

通过对测试问卷进行回收与统计分析，所得结果如表2所示。由表1中对应关系可知，分值为6分、12分、18分、30分、34分、36分分别对应6个能力等级，表2中结果显示得分为30分的人数最多，达到37人，占总人数的47%。

由表2中结果可知，接受本次测试的79名学生数学建模能力测试结果与预期存在一定差距。调查结果明确显示，学生在除设定变量参数及常数、数学化陈述问题以外的其他步骤建模能力较为薄弱。出现此情况的主要原因在于教师并不重视培养学生的数学建模能力，实际教学过程仍未脱离传统基本概念与运算知识讲解、技能训练的教学模式。

三、学生数学建模能力影响因素

（一）数学基础知识掌握程度

大部分学生对数学基础知识的掌握程度较低，数学理解与应用能力较弱，难以接受高等数学学习内容。不仅如此，在高职数学教学中，很少有学生能接触到数学建模，选修数学建模课程的学生也相对较少。

（二）实际问题背景理解

数学建模是指从现实生活中提炼出数学问题，通过寻找变量间关系，构建出与之相对应数学模型，然后运用数学知识去解决相关问题，其涉及问题较为广泛。大部分高职学生数学阅读水平不高，对题干较长题目接触频次较低，未接受过专门训练，所以理解相关题目比较困难，解读实际问题背景也较为困难。

（三）建模问题简化与假设

现实中复杂而多变的问题，其影响因素来源于多个方面，很难做到面面俱到。所以，在构建数学模型的过程中，学生必须在相应假设条件下才能展开研究。如果没有进行必要合理的简化和假设，就很难将实际问题转化为数学问题。模型构建成败主要依赖于假定是否恰当，而假定不同将导致模型构建结果不同。对学生而言，建模问题假设是最困难和最重要的环节。多数学生在运用数学知识解决生活中的实际问题时，缺乏对现实问题情境的理解，不能通过简单假设提炼数学问题。

四、基于数学建模能力培养的高职数学教学对策

（一）以培养学生建模能力应用意识为指导组织教学内容

数学建模思想在高职数学教学中占有重要的地位，这不仅是因为数学建模是现代科学技术发展的重要组成部分，还是因为数学建模能够帮助学生更好地理解和应用数学知识。因此，教师应将“用”作为切入点，引导学生掌握数学建模能力。

首先，教师应将重点放在教授学生如何运用数学建模知识解决实际问题上，而不是仅仅教授理论知识。对此，教师可以将现实生活中的问题融入课堂，让学生参与到数学建模过程中，培养学生解决实际问题的能力。

其次，教师可以对学生进行科学、有效的引导，提高学生的认知水平和思考能力。通过引导学生思考实际问题，并将问题转换为数学模型，教师能帮助学生在思考过程中逐渐养成科学的思维方式。这不仅可以提高學生的数学建模能力，还可以在日常生活中培养学生科学的思考方式，提高学生的综合素质。

最后，教师需要把握好教学节奏，在验证、分析的过程中，提高学生的数学建模能力，培养学生的数学建模意识。在教学过程中，教师应不断加强对学生的引导和帮助，让学生在实际操作中不断提高数学建模能力，并且在分析和验证过程中逐渐培养学生的数学建模意识。

总之，数学建模思想在高职数学教学中极为重要。通过将“用”作为切入点，教师可以引导学生运用数学建模知识解决实际问题，提高学生的数学建模能力，培养学生科学的思考方式和解决问题的能力。

（二）立足知识点培养学生数学建模能力

在实际工作中，教师应基于培养应用型人才这一核心定位，充分遵循“以生为本、学以致用”原则，立足具体的知识点渗透数学建模思维，循序渐进地引领学生掌握数学建模的相关知识并深化对相关知识点的理解，最终达成培养学生数学建模能力的目标。

以数学概念知识点为例，高职数学教材中包含较多概念性知识，而传统教学理念主要采取“灌输式”教学，学生难以具象化构建出相应的知识框架，在实际学习过程中也难以灵活使用概念性知识。因此，教师可以将数学建模思维渗入教学过程中，列举出与学生有密切关系的实例，引领学生探索数学概念与现实生活之间的关系，并深入认识不同数学概念在现实生活中的应用场合、运用价值、意义等，激发学生学习数学建模相关知识的兴趣。

比如，在讲授函数时，教师可以引用人口增长案例，指导学生建立对应的指数模型，或者从经济运行规律、个人情绪周期变化等角度列出相应实例，指导学生建立三角函数模型。在高职数学知识体系中，导数知识占据重要地位。在教学过程中，教师应利用系统化教学方法指导学生掌握一阶、二阶导数求函数极值，求实际问题最值等核心知识。在此过程中，教师如果仅依靠单一、抽象的数学问题指导学生掌握相关的关键知识，很难达到理想的教学效果。为有效提高学生对重点知识的学习效率，教师可以主动地运用数学建模思想，与现实案例进行结合。例如，教师运用微分求极大值法，可以解决医院转角的设计问题、电影院优化问题、游乐设备安全问题等。在导数知识建立的数学模型辅助下，学生能深入理解和把握导数的使用意义。

综上所述，在当前教学改革背景下，教师将数学建模知识渗入高职数学教学，可以有效提高教学效率。因此，在实际工作中，教师应重视学生的思维发展规律和特点，将数学建模知识逐渐渗透到教学内容与教学过程中，从多个层面培养学生的数学建模意识和能力，为提高高职数学教学效率提供有力保障。

参考文献：

[1]丁玥，李玮玲.基于数学建模能力培养的教学策略探究[J].学周刊，2022（7）.

[2]孙平利.高职高专数学建模方法的策略研究[J].包装世界，2021（5）.

[3]刘宇航.基于数学建模的高职经济数学“教学做”一体化教学[J].休闲，2021（1）.

[4]齐峰.数学建模思想在高职数学教学改革中的应用[J].读与写（上旬），2021（9）.

[5]梁岩，李晓辉.将数学建模思想融入高职数学课堂的思考[J].数学学习与研究，2021（18）.

[6]郑毅斌，韩宇.基于关键能力培养的高中数学建模课堂教学研究：以“建模初体验：汽车紧急刹车情况下的停车距离问题”为例[J].新课程教学（电子版），2022（12）.

基金项目：2021年11月江苏省教育厅“高职院校公共基础课程建设与教学改革研究”，項目编号：2021JSJG516。