基于GAIN-LSTM网络的雷达PRI序列还原及识别方法*
2024-03-26李忠媛龚晓峰雒瑞森
李忠媛,鲜 果,龚晓峰,雒瑞森
(1.四川大学 电气工程学院,成都 610065;2.成都大公博创信息技术有限公司,成都 610065)
0 引 言
雷达信号的脉冲重复间隔(Pulse Repetition Interval,PRI)指辐射源发射脉冲的重复时间间隔,是用于雷达辐射源型号识别和雷达工作状态估计的主要参数。它具有多种模式,与雷达工作性能、工作体制有着直接密切的关系[1]。开展PRI调制模式识别对于雷达辐射源识别及威胁分析具有重要意义。
PRI调制模式的传统识别方法主要是直方图法[2-3]、PRI变换法[4]以及基于它们的变式[5-9]。这些方法通过脉冲分布数量统计或结合其他手工提取的特征,可以实现简单体制雷达的分类识别。对于复杂PRI调制识别,由于深度学习在图像、文本分类识别方面的有效性[10],近年来许多学者也将神经网络运用到该问题上。Liu等人[11]利用多层神经网络对四种PRI调制进行分类,但需要手动提取PRI序列相关特征。Feng等人[12]设计了一种带有向量化嵌入和压缩-激励注意力机制的多尺度卷积块来进行特征提取,然后利用网络层进行分类识别。这类方法主要集中在特征提取上,并不是利用PRI序列本身规律进行分选。
在现代电磁环境中,受复杂信号环境接收脉冲发生碰撞、接收条件的限制(雷达天线旋转扫描)以及低截获概率技术的发展等影响,大量雷达脉冲无法被接收,丢失脉冲率高,导致分选出的PRI序列规律性被破坏,现有PRI识别方法准确率不足。当前研究人员也对脉冲高丢失率情况下的PRI识别进行了一些有益的探讨。Li等人[13]通过搭建卷积神经网络实现了7种PRI调制类型的自动识别,在脉冲缺失率50%条件下能达到96%的识别精度。孟等人[14]考虑到PRI是时序数据,利用均值替换法对数据进行预处理后,采用长短时记忆网络对不同体制雷达进行分类识别,在脉冲丢失率不大于30%时能实现较好的识别效果。另外,深度自编码器(Deep Auto-Encoding,DAE)[15]、全卷积深度学习网络(Fully Convolutional Network,FCN)[16]也被用于PRI调制模式识别。上述方法无需手动提取特征,提供“端对端”的识别过程,但都是通过大量数据进行模型训练以提高分类精度,对脉冲丢失情况数据未做分析处理。
考虑到脉冲丢失率过大时对识别效果的不利影响,本文从另一个角度——缺失数据补全角度出发,探索了基于深度学习的数据补全方法[17-18]。GAIN(Generative Adversarial Imputation Nets)是基于生成式对抗网络的序列补全方法,在多领域数据集上获得了良好的补全效果[18]。本文通过GAIN对有缺失数据的PRI序列实现还原,恢复不同体制PRI变化规律,同时结合PRI序列本质是一维时间序列的特征,利用长短期记忆(Long Short Term Memory,LSTM)网络对补全时序数据进行分类识别。由此搭建的GAIN-LSTM网络架构,通过对PRI序列进行特征自动提取,实现PRI还原和识别功能。仿真生成了多种调制类型的样本集,测试了脉冲丢失数据补全效果以及在不同条件下的PRI模式识别性能,为该方法进一步研究和工程应用提供了有益参考。
1 PRI调制模式分析
接收机截获雷达辐射源脉冲信号,相邻脉冲到达时间的间隔即是脉冲重复间隔,用函数定义如下:
P={p1,p2,…,pN},pi=ti+1-ti
(1)
式中:{ti,i=1,2,…,N+1}是雷达脉冲流中各个脉冲的到达时间,N+1为当前所分析雷达脉冲串中所包含的雷达脉冲个数。
雷达辐射源根据任务需求,通过调整PRI变换规律实现不同的功能模式[20]。表1描述了6种典型雷达辐射源PRI调制类型的PRI变化规律和相关应用场景。
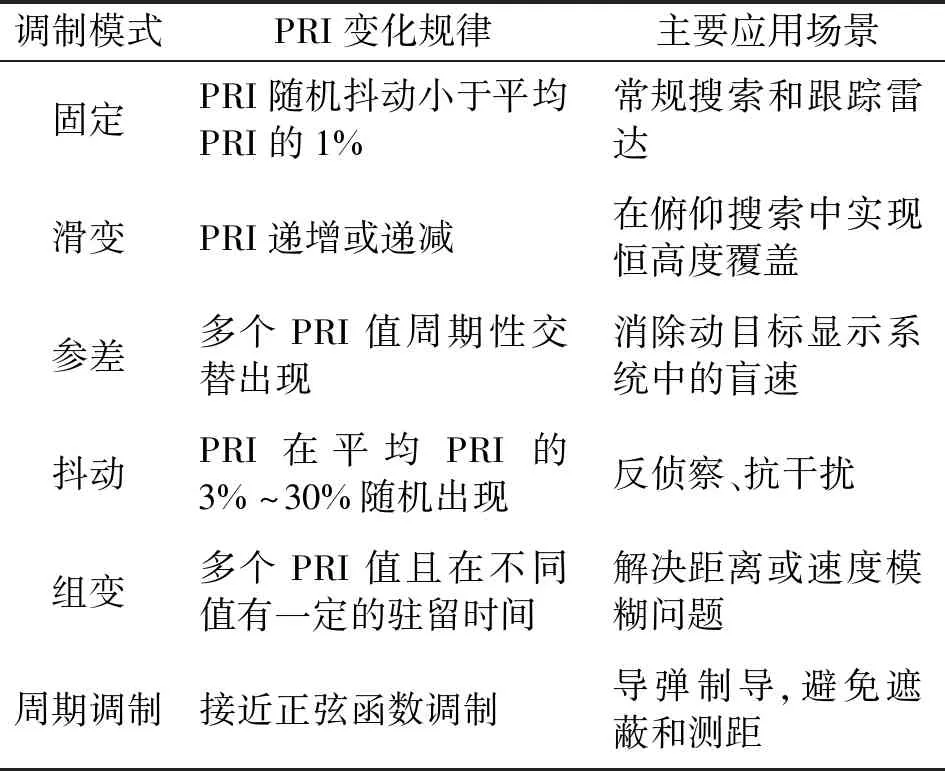
表1 典型雷达辐射源PRI调制类型及应用场景[19]Tab.1 Typical PRI modulation types and application scenarios
图1展示了不同脉冲重复间隔调制模式序列的PRI分布图,横坐标表示PRI序列个数,此处展示PRI序列长度为50,纵坐标为PRI归一化值。图1(a)是理想情况下PRI分布图,可见在完整侦收雷达脉冲的情况下,PRI分布完全符合PRI调制规律。然而,受复杂电磁环境和接收设备本身的影响,雷达侦察机接收到的辐射源脉冲是各种辐射源和随机噪声信号相互交叠的混叠脉冲流,且接收过程中常出现丢失脉冲的现象,分选后雷达PRI变化规律被破坏,图1(b)展示了实际情况下PRI分布情况。我们的目的在于还原这些因脉冲丢失导致的错误PRI值,进而完成PRI调制模式识别。
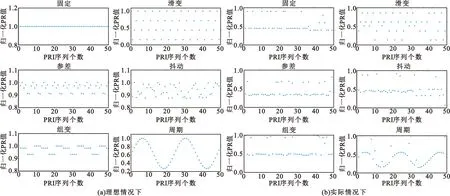
图1 不同PRI调制模式雷达信号的PRI分布Fig.1 Distribution of PRI in different modulation modes
2 GAIN-LSTM模型描述
2.1 问题描述
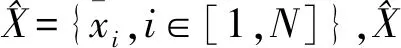
图2 基于GAIN-LSTM的PRI序列还原及体制识别架构Fig.2 PRI sequence restoration and modulation modes recognition architecture based on GAIN-LSTM
2.2 数据处理
基于雷达脉冲流的到达时间(Time of Arrival,TOA)序列,由式(1)求取一阶差分获取PRI时,如果发生脉冲丢失,相应就会产生数值增加的虚假PRI值,即异常值,多个脉冲连续丢失,导致虚假PRI值成倍增加,原有PRI变化规律就被严重破坏。通常采用的虚假PRI异常值处理方法是用均值替代[14]。本文通过均值比较检索PRI异常值,并通过填充“*”的方式标记PRI待补全位置,公式描述如下:
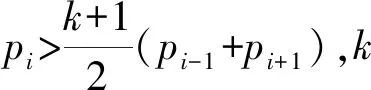
(2)
式中:N表示处理脉冲段PRI总数量数,如果当前PRI值大于前后PRI值均值(k=1),认为此处漏掉一个脉冲,用“*”补该位置空缺;如果大于均值2倍(k=2),认为此处漏掉两个脉冲,相应地在此处填补两个“*”。以此类推。
经上述处理获取输入原始向量X,表征PRI序列,缺失值位置已用‘*’标记。根据X生成对应掩码向量M={mi},M为二值矩阵,真实值位置为1,缺失值位置为0。定义新向量Z,大小等同X,在缺失值位置随机生成噪声作为填充,相当于初始化。
2.3 GAIN序列还原网络
整体网络包括生成器(Generator,G)、判别器(Discriminator,D)、提示机制(Hint,H)三部分。G通过观察真实数据的分布和内部联系,根据观察结果填补缺失的部分,输出一个填补后完整的向量并送入到D。D需要判断接收向量中,哪一部分是真实数据,哪一部分是填补的。D最小化分类误差率,而G要最大化判别器的分类误差率,这样两者就处在了一种相互对抗的过程中。为了使该对抗过程得到更加理想的结果,添加了提示机制H,它揭示了原始数据中缺失部分的某些信息,让D更加关注它所提示的部分,同时也使G生成更加接近真实分布的填补数据。具体介绍如下。
2.3.1 生成器G
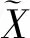
(3)
(4)
2.3.2 判别器D
判别器D被用作对手训练生成器G。不同于标准生成对抗网络,这里的判别器D判断输入向量中哪些部分是真实的,哪些部分是估算生成的,这相当于预测掩码向量,其输出的值意味着预测该值是原始真实值的概率。在图2右侧,判别器的输出与掩码向量的交叉熵损失同时作用于生成器G和判别器D。
2.3.3 提示机制H
提示机制是一个随机变量H,H中的元素h依赖于分布H|M=m,其与生成向量横向结合后输入到D中,用以提示D更需要关注的部分,强化了G和D的对抗过程。
2.3.4 优化目标
类似于生成对抗网络,通过最大化正确预测M的概率来训练D,通过最小化D能正确预测M的概率来训练G,定义如下的评估函数:

(5)
因此GAIN的目标就是
(6)
因为对于判别器来说就是一个简单的二分类问题,所以这里就使用交叉熵来定义损失函数,如下所示:
L(a,b)=ailgbi+(1-ai)lg(1-bi)
(7)
(8)
训练过程中固定一方,更新另一个网络的参数,交替迭代,使得对方的错误最大化,最终G能根据学习到的数据分布规律估算出更合理的缺失值。
2.4 LSTM识别网络
GAIN网络对雷达PRI序列缺失位置填补后生成向量是LSTM识别网络的输入,设输入向量长度为N。如图3所示,输入至LSTM单元构成的隐藏层神经网络,最后一个LSTM单元的输出作为输出层的输入,输出层输出结果反向传播至隐藏层进行网络训练。具体介绍如下。
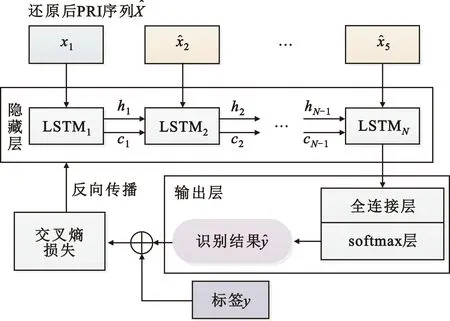
图3 基于LSTM的雷达PRI序列识别网络Fig.3 PRI modulation modes recognition network based on LSTM
2.4.1 隐藏层
各个PRI值依次输入N个LSTM单元。LSTM单元传递过程可描述如下:引入输入门限it、遗忘门限ft、输出门限ot以及记忆细胞ct。利用记忆细胞记录网络的长期状态,并通过3个门限对记忆的丢弃、增加以及读取进行控制。3个门限更新计算方式表示为
(9)
式中:W和b分别是对应的权重系数和偏置系数。每个LSTM单元接收当前输入xt、前一个单元的ht-1和ct-1为输入,即在获得上一时刻的单元状态的前提下进行运算,用T代指tanh激活函数,ht和ct更新过程如下:
ct=it·T(xt·Wxg+ht-1·Whg+bg)+ft·ct-1
(10)
ht=ot·tanh(ct)
(11)
2.4.2 输出层
输出层由全连接层和softmax层组成,隐藏层的输出接入全连接层,softmax层输出分类结果。本文对6种典型PRI体制进行分选识别,标签为6位one-hot编码,采用softmax函数结合交叉熵损失函数进行单标签分类,通过时间反向传播算法对网络进行训练。
3 实验设置
3.1 仿真条件
通过深度学习平台tensorflow完成网络的搭建。训练和测试网络使用服务器CPU为Intel(R) Core(TM) i5-7500,GPU为NVIDIA GeForce GTX 3070。网络训练以损失函数最小为目标,利用反向传播算法不断迭代更新网络参数,得到最终的PRI序列还原和识别网络。
3.2 仿真数据
雷达侦察机实际接收到的数据存在脉冲碰撞和虚假脉冲等问题,通过载频、脉宽、到达角等脉内参数进行聚类分选得到的雷达脉冲序列脉冲丢失严重,同时脉冲数量不固定,需要对分选后PRI序列样本进行预处理以适应模型输入。这里根据表2中仿真生成脉冲数量不一致的各种PRI体制雷达脉冲序列,包含不同脉冲丢失率各20万条样本。根据2.2小节对样本进行待补全位置标记操作,获取原始PRI序列。
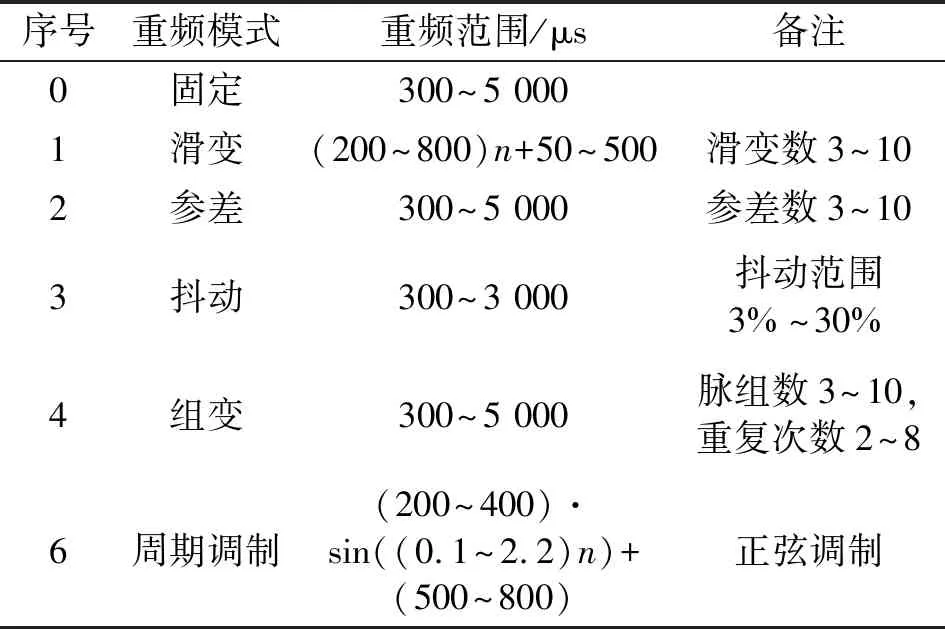
表2 仿真数据设置Tab.2 Setting of dataset parameters
因为涉及到通过LSTM对补全PRI的识别过程,送入样本长度因与LSTM隐藏层包含的时间迭代单元数量保持一致,故需要做统一样本长度处理。设需要将样本统一变换为N,对长度为m的PRI序列,m
(12)
样本标签需要转换成one-hot编码。
4 实验及结果分析
4.1 PRI序列使用GAIN网络的还原对比
为了验证搭建的GAIN模型对脉冲丢失样本的PRI序列还原效果,与文献[16]中自编码器还原方法进行对比实验,使用均方根误差(Root Mean Square Error,RMSE)为评价指标,衡量丢失数据部分的重构误差。其计算公式如下:
(13)
表3记录了PRI序列长度100、脉冲丢失率30%条件下,分别利用自编码器和GAIN对PRI序列进行还原的效果。对不同PRI调制模式的仿真数据进行分层采样,各模式1万条共计6万条数据,并随机打乱样本顺序,送入GAIN网络重构,进行10次实验,取平均结果。可见,对于不同PRI调制模式,GAIN都有更好的重构效果,而抖动、参差、组变由于PRI值的随机性,重构RMSE相较于其他调制模式略大一点。图4展示了10%~80%脉冲丢失率条件下,两种方法对各类调制模式的平均重构误差曲线。脉冲丢失率小于60%条件下,GAIN方法重构RMSE始终保持在0.04左右,相较于自动编码方法高出10%以上。
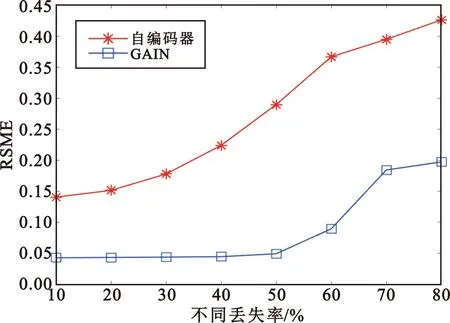
图4 不同脉冲丢失率下重构误差Fig.4 Reconstruction error under different pulse loss rates
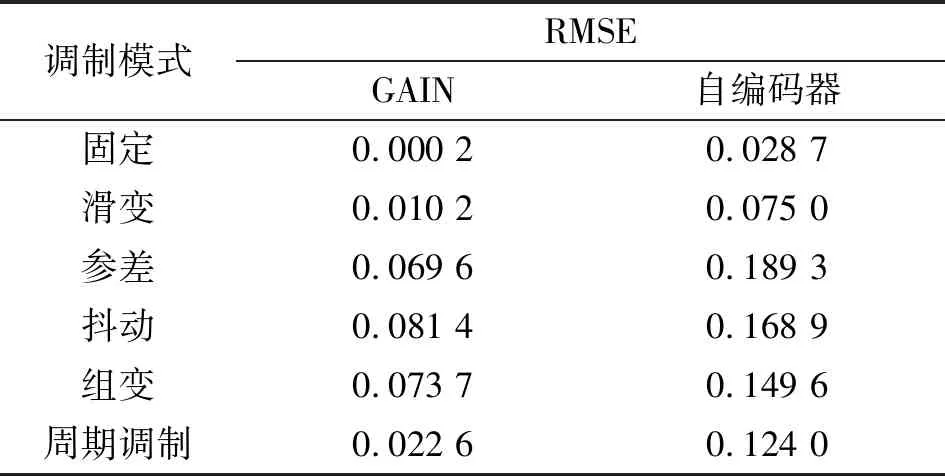
表3 GAIN与自编码器重构误差Tab.3 Comparison of reconstruction errors between GAIN and autoencoder
4.2 PRI调制模式识别性能验证
为了反映模型的准确性,对PRI序列长度100,30%脉冲丢失率的10万条包含不同PRI调制模式的数据集,进行5折交叉验证,其对应测试集的识别率统计在表4中,可见,各自的识别率保持在同一水平,说明模型是稳定的。
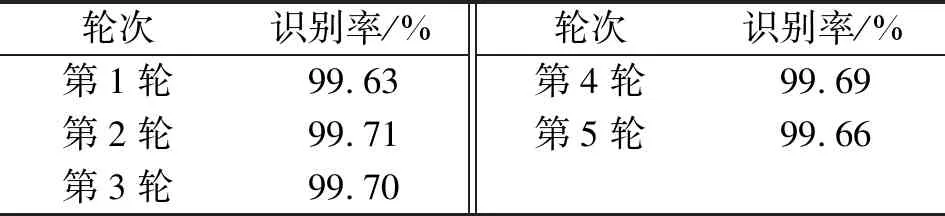
表4 5轮训练模型识别率Tab.4 Model accuracy under five rounds of training
为了验证网络的识别性能,分别测试不同脉冲丢失率和不同序列长度对模型识别性能的影响。首先,统计固定序列长度100,10%~80%脉冲丢失率下的各种PRI调制模式识别结果,如图5所示。
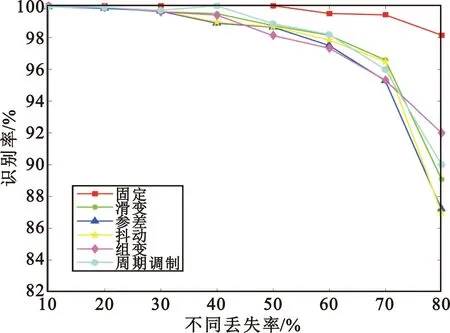
图5 不同脉冲丢失率下GAIN-LSTM网络识别率Fig.5 Recognition accuracy of GAIN-LSTM network under different pulse loss rates
由图5可见,所提方法对各种PRI调制模式识别率均保持在较高水平,在脉冲丢失率超过50%时,识别率随丢失率增大而下降且下降速度加快。但脉冲丢失率为70%时,对各种PRI调制模式识别率仍都在95%以上,这说明脉冲丢失极为显著情况下,所提序列还原再识别方法具有可靠的识别效果。
图6展示了固定脉冲丢失率30%,不同PRI序列长度下的识别率曲线。在序列长度大于35时,模型平均识别率超过98%;小于35时,组变、参差调制模式识别率下降,周期、滑变模式识别率也略微下降,这是由于序列长度过短且存在30%的脉冲丢失率时,这几类长周期变化规律难以被学习到,导致在序列还原及模式识别时,特征提取不足,对最终识别率造成影响。但值得一提的是,在脉冲丢失率30%,序列长度为20时,所提方法仍有92.2%的平均识别率。
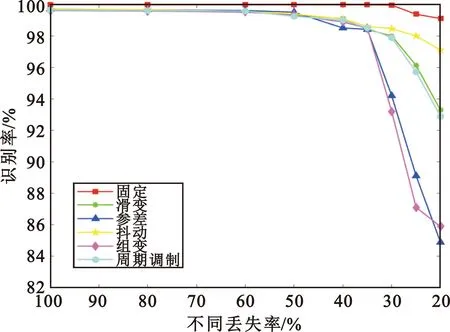
图6 不同序列长度下GAIN-LSTM网络识别率Fig.6 Recognition accuracy of GAIN-LSTM network under different pulse sequence lengths
4.3 PRI调制模式识别效果对比
将所提方法与CNN[13]、DAE[16]、LSTM[14]等当前先进PRI调制模式识别模型进行对比实验。同时,为了进一步验证GAIN网络对PRI序列的还原效果,对GAIN网络进行还原后的PRI序列,也送入上述各识别模型进行还原前后识别效果对比。
图7绘制了6种模型对各类PRI调制模式平均识别率曲线,虚线展示了3种识别模型的识别效果,相同颜色的实线曲线对应于加上GAIN序列还原模块的模型识别效果。可见,添加GAIN还原模块的模型,其识别率均有所提升,这说明对PRI序列进行还原,恢复其PRI变换规律,是提升高脉冲丢失率序列分类识别率的有效手段。
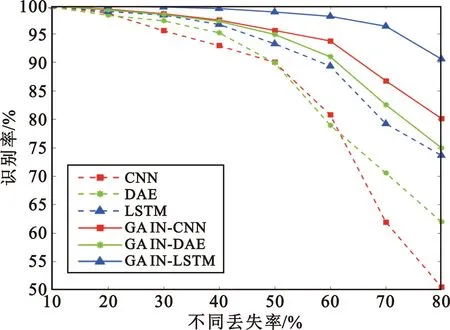
图7 不同脉冲丢失率下不同模型识别率Fig.7 Recognition accuracy of different models under different pulse loss rates
而在所有模型中,其识别率都随脉冲丢失率增大而有所降低,可见,脉冲丢失对各种直接基于PRI序列的模型识别效果都有直接影响,在脉冲丢失率过大时,现有方法CNN、DAE、LSTM的识别率剧烈下降,蓝色实线展示的所提方法识别率曲线则平缓得多。本文所提GAIN-LSTM显著优于其他网络模型,在脉冲丢失率过大时优势更为显著,在脉冲丢失率为70%时仍有96.33%的平均识别准确率。
5 结 论
针对常见的由于脉冲碰撞导致的高脉冲丢失率场景,本文提出了一种GAIN-LSTM架构,通过缺失数据补全还原真实PRI序列,恢复PRI变化规律,再由还原后序列进行模式识别,对于雷达脉冲丢失率显著的PRI调制模式识别准确率大大提升。现代复杂电磁场景下,常见高密度雷达脉冲流和多部雷达辐射源混叠情形,脉冲碰撞和虚假脉冲出现的几率大幅增加,本文提出的模型可应用于上述脉冲丢失率极端场景,恢复脉冲序列规律,准确识别PRI调制模式。
