成熟因子映射的双系统选星方法*

李 想,孙 鼎,安 毅,陈 勇,滕云龙

(1.电子科技大学 机械与电气工程学院,成都 611731;2.中国西南电子技术研究所,成都 610036;3.海装重大项目中心,北京 100071)

0 引 言

在卫星导航接收机进行选星过程中,传统方法主要以几何精度因子(Geometric Dilution of Precision,GDOP)为依据,采用遍历的方式搜索最优集合,或通过几何构型选出经验解。对于遍历的方法来说,可见星的数目决定其运算次数。对于几何构型方法来说,几何构型随着选星数量的增加越来越复杂,且实际操作时为找出体积最大的解,往往也要进行遍历。由于当前接收机可以接收到大量可见星[1-3],传统的选星方法难以在短时下得出合适的选星集合。在实际的工程场景下,基于遍历的传统选星方法难以胜任。

遗传算法对于优化非线性等复杂问题具有独特的优势[4]。当前已存在一些遗传算法选星的研究。与传统方法相比,遗传算法可以不经过遍历就可以得到次优解或最优解。宋丹等人[5]提出了一种基于遗传算法的选星方法,在交叉和变异中穿插了优选过程,避免了进行个体淘汰,并通过实验确定了遗传算法选星的参数规律,并给出了推荐的参数方案。陈灿辉等人[6]提出了一种基于二进制编码的交叉算子,用变异操作来辅助交叉,使得基因交换既可以双向传递也可以单向传递,使得交叉概率高于50%时与互补交叉概率有所区别,这种变异算子实际上把变异操作和交叉操作糅合,变相增大了变异概率。霍航宇等人[7]提出了一种基于遗传算法的组合系统选星方法,从选星数量角度减少了运算量。这些研究基本上都固定了交叉和变异的概率,且如果算子相互糅合,参数量化规律会有一定的偏差。Zhu[8]对交叉和变异概率进行了改进,但是这种方法是基于适应度的密集程度来进行映射的,需要遍历当前种群的适应度,计算相对复杂,且密集程度的判断标准由于算例不同很难界定。综上所述,对于交叉和变异概率的改进仍需要继续研究。

针对上述问题,本文提出了基于种群数量控制与成熟因子映射的双系统遗传选星算法。相较于其它遗传算法选星方案,本文提出计算相对简单的成熟因子来反映种群基因的相似程度,并根据成熟因子调整交叉和变异的概率,一方面避免种群过早成熟陷入局部最优,另一方面节省交叉和变异的操作时长。此外,本文方法通过引入种群数量控制策略,可以避免较后子代种群数量过大而迭代过慢的情况,在保证选星集合的GDOP搜索精度的同时可以有效降低计算量。

1 基本定义

1.1 成熟因子

成熟因子FM是对整个种群在交叉、变异操作后种群个体变得更加优良的可能性的一种表征。依据当前种群成熟因子的大小对交叉与变异操作进行修改,以引导种群更好地“进化”。

在基因库过于单调且变异机率较低的情况下,个体的变化几乎只依赖于重组,使得种群多样性不足,选星结果容易陷入局部最优,即出现早熟现象,因此本文将种群个体间的相似程度作为构建成熟因子FM的基础,具体为当前种群前5个数量最多的基因的占比之和:

(1)

式中:Num(·)表示·的数目;Xj,Xk,Xl,Xm,Xn分别为当前种群中数量最多的前5个基因。

基于成熟因子映射实际上是通过对当前种群基因库的多样性进行评估,具体映射于交叉概率和变异概率的阶梯变化。基因重复度过高,成熟度也越高,代表当前的种群基因库已经进行了较多重组尝试,此时在保留优势个体的前提下增加种群的多样性;相反,种群基因重复度不高时,应该优先探索当前基因库的潜力,找出其中可能造成GDOP优势的基因组合。

1.2 适应度及双系统GDOP计算

几何精度因子表征由几何布局而产生的定位误差相对于伪距测量误差的放大倍数,用于评估选星集合的优劣[9]。根据文献[10],GDOP的评价标准见表1。

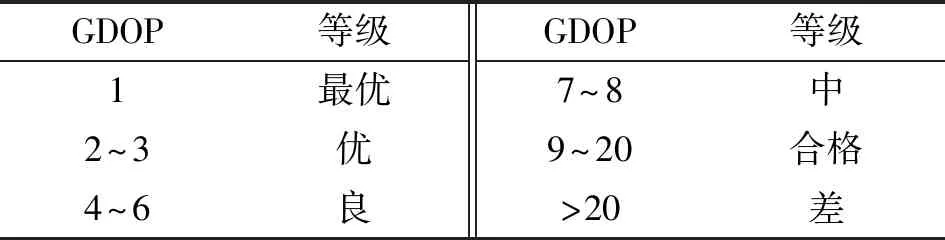
表1 GDOP评价标准Tab.1 Evaluation criteria for GDOP

(2)

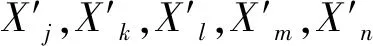
在计算双系统GDOP时,观测矩阵钟差参数系数的位置取决于参与运算的卫星所属的系统。双系统几何观测矩阵的形式如下[11]:

(3)

2 基于成熟因子映射的选星方法

选星问题实际上是寻找以GDOP值为评价标准的最优或次优卫星组合,因此本文对遗传因子(对应于具体的卫星位置信息)采用序列编码,即按照星历中卫星的顺序对卫星进行对应的实数编码,将所需数量的卫星序号组合为染色体。当需要计算染色体的适应度时,在可选卫星列表中查找序号对应的卫星具体位置信息进行计算。由于各系统卫星在星历文件中的顺序是邻近的,通过序号也可以对所选卫星的系统进行标定,从而调整几何观测矩阵的形式,使其适应双系统GDOP的计算。对于选星时可能会碰到5颗卫星均来自同一系统的情况,以固定几何观测矩阵的形式依然可以通过虚拟一个相同的钟差参数完成计算。

基于成熟因子映射的选星方法流程如图1所示,选星算法主要包括获取初始种群、父代选取和复制、成熟因子指导交叉、成熟因子指导变异、种群数量控制以及收敛判断等关键步骤。

图1 选星算法流程Fig.1 Flowchart of the satellite selection algorithm

1)获取初始种群

遗传算法是一种随机搜索算法[12],初始种群的选取应该既体现出随机性又能尽量体现样本的统计特征。Sobol序列是一种构造方法简单、分布均匀的低差异序列,相较于伪随机数产生的序列更加均匀。因此,本文首先生成3组长度为可选卫星总数的Sobol序列,对Sobol序列值的大小进行排序,并记录下原序列的索引,得到分布均匀的低差异整数序列。将序列分割为长度为5的序列段构成各个单染色体个体的染色体,长度不足5的暂不构成染体,但仍然保留作为变异备选,这些个体构成初始种群。因此,初始种群的大小基本上和待选的可见星颗数的3/5保持一致。

2)父代选取和复制

为保留每代最优GDOP指标,需要将适应度最高的个体复制到下一代,将适应度病态的个体直接剔除,剩下的种群按等间距多指针轮盘法进行选择和复制。

3)成熟因子指导交叉

交叉实际上是基因库内部组合的尝试,本文采取均匀交叉,即每个基因位点均有可能发生单个位点的基因交换。由于均匀交叉实际是两个单染色体个体各自位点基因进行交换,从概率上可以认为每条染色体交换基因占比期望与交换概率相等,而两条染色体交换一定比例的基因和交换互补比例的互补位点基因是一样的,因此认为单纯交换操作中交换概率能够发挥作用的上限实际上是50%。在成熟度较高的时候可以认为当前种群基因库已经经过较为充分的组合,为节省运算,可以降低此时的交换概率。本文将成熟因子FM分段映射为交叉概率Pcross指导每个基因交换的操作。交叉概率Pcross映射函数为

(4)

4)成熟因子指导变异

将交叉后的个体进行均匀变异操作。变异实际上是种群内部基因库和整个可见星集合基因库的基因交流。已有文献说明遗传算法解决选星问题时,为避免陷入局部最优,变异概率应当取较高的值,但是变异操作需要随机选取和检索剩余基因库需要较长的运算时间,高变异率意味着频繁的变异操作,也会导致遗传算法相同迭代数内的搜索时长增加。在成熟度较低的时候,种群基因多样性较丰富,可以降低变异概率,让基因充分组合,探索合适的选星集合,并减少变异操作的时长;在成熟度较高的时候,种群基因多样性较匮乏,可以提高变异概率,加强基因交流。本文将成熟因子FM分段映射为交叉概率Pmutate指导每个基因交换的操作。交叉概率Pmutate映射函数为

(5)

经过交叉变异的种群连同适应度最高的精英个体一同组成下一代种群的备选集合。

5)种群数量控制

由于选星算法初始种群个体数与可见星个数有关,因此在可见星较多的情况下,种群个体数较多,需要多次计算适应度,运算成本较高。本文采取判断种群是否超过限额的策略进行数量控制,将适应度最低的一批个体淘汰。由于最优保留策略,种群数每代会累加1,限额淘汰可以使种群数量在限额附近波动,既可减少总的运算次数,也能在种群繁盛期进行更多的交叉重组尝试,从而减少后续子代种群过大、代内计算过久的情况。本文采取的限额为初始种群数量的1.5倍,每次淘汰对应GDOP值最差的20%个体。

6)收敛判断

由于遗传算法是随机搜索算法,虽然在采取精英保留策略[13]的情况下可保证收敛到最优解,但收敛时间存在着不确定性,实际应用时应使用可接受最大GDOP门限或者进化代数门限进行收敛判断,当满足收敛条件时跳出进化迭代,输出选星集合。

网络新媒体传播具有开放性、即时性、互动性等特点，深受普通民众青睐，越来越多的网民群众在新媒体平台和渠道上发布观点意见，表达利益诉求，产生了大量的舆情民意信息。地方政府部门通过对这些信息的收集和分析，能够更好地了解本地公众需求，有针对性地采取政策措施，提供公共产品和服务，及时发现和化解社会矛盾，不断提升治理效能。同样，地方政府利用新媒体打造与公众直接对话的交流平台，传递政府决策信息；并借助新媒体技术实现公共决策的多方参与和公开透明，从而促进地方政府治理能力提升。

3 实验与分析

从欧洲轨道测定中心(Center for Orbit Determination in Europe,CODE)发布的MGEX轨道钟差文件2023年1月30日0时0分0秒中的轨道数据中,选取来自两个系统的30颗俯仰角大于10°的卫星(其中GPS卫星10颗,BDS卫星20颗),选取的接收机三维坐标为[-2 168 839.180 m,4 386 630.094 m,4 077 164.910 m]。

3.1 选星性能对比

传统的遍历法选出的是最优解,搜索时间也比较稳定,可以作为评价选星结果的标准,因此将结果单独列出。对于上述30颗可见卫星集合而言,遍历算法选星结果如表2所示。

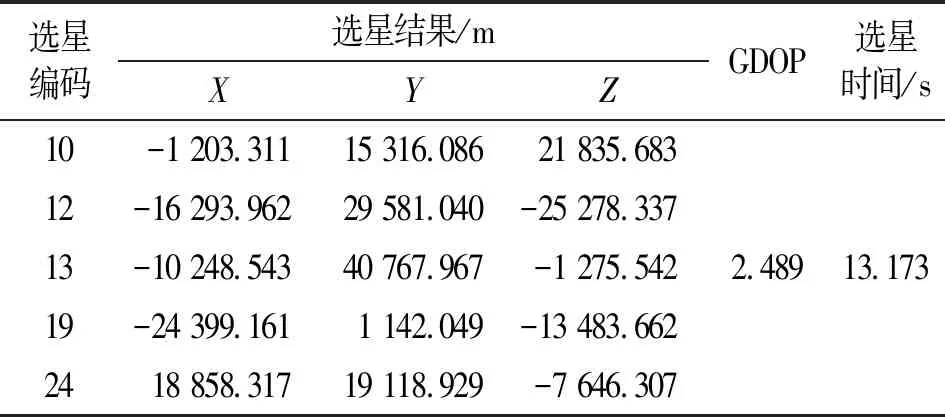
表2 遍历算法选星结果Tab.2 Results of the traversal algorithm for satellite selection

由于遗传算法通常具有不确定性,所以实验结果应该采取统计结果。按照前文所述选星参数标准和可见星数为30,此时初始种群数量为18,种群数量限额为27。本文对比所用的常规遗传算法主体结构参考了文献[14],各个主要环节有多种可选的方案,为了更直观地体现改进点的效果,基于控制变量原则,除去成熟因子和种群数量控制相关的改进点外所选用机制均与本方法保持一致,交叉概率和变异概率则设为文献[5,8]提供的最优方案,即Pcross=0.9,Pmutate=0.9。测试发现,Pmutate=0.9时配精英保留策略能够尽快跳出局部最优,但相同代数需要的搜索时间更长,与文献[5]结论一致;Pcross对相同代数搜索精度的影响则不明显。

设定进化代数为200,分别进行常规遗传算法、成熟因子映射遗传算法和引入种群数量控制的成熟因子遗传算法各500次搜索,记录每代GDOP最优值,统计500次实验每代最优组合对应GDOP平均值构成200代内的最优个体GDOP进化曲线,如图2所示。

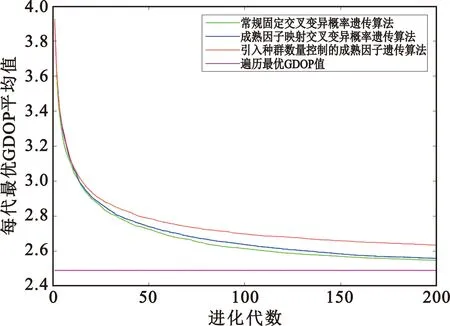
图2 进化200代种群最优GDOP进化对比Fig.2 Comparison of optimal GDOP evolution for populations of 200 evolutionary generations

记录下进化代数200代平均搜索时间,如表3所示。

表3 进化200代平均搜索时间Tab.3 Average search time of 200 evolutionary generations

由图2和表3可知,成熟因子映射交叉变异概率遗传算法相较常规固定交叉变异概率遗传算法在相同进化代数的搜索效率没有明显的差别,但是在相同代数内,成熟因子映射遗传算法比固定交叉变异概率的常规遗传算法平均节省约24.75%的搜索时间,这是由于成熟因子映射成功减少了不必要的交叉和变异操作。在此基础上引入种群数量控制机制,相同代数下的搜索效率有所下降,但进化200代内搜索时间进一步节省了约55.32%。这是由于种群数量控制实际上减少了每代遍历的个体数,一方面,每代检索效率难免会有所下降;另一方面,随着代数推进,相较于不断增长的种群数量,每一代搜索时间的优势会越来越大。实际上在本节参数设定下,成熟因子映射交叉变异概率遗传算法迭代到最优组合总耗时比常规遗传算法减少约4.20%,引入种群数量控制的成熟因子遗传算法迭代到最优组合总耗时仍然比常规遗传算法减少约5.41%。

相较于耗费大量时间搜索最优星座集合,在实际选星时,更倾向于选出保证解算精度的可用解。根据表1中GDOP评估标准,本文设置GDOP的门限为3,对3种方案分别进行10 000次搜索,统计搜索时间平均值,如表4所示。

表4 GDOP门限为3时平均搜索时间Tab.4 Average search time when GDOP threshold is 3

根据图2可得,设定门限为3时3种方法的搜索性能相近,且迭代数平均不到20代,在迭代次数较小的情况下,成熟因子映射和种群数量控制在大多数实验中起的作用不大,但是实测数据中成熟因子映射遗传算法较常规算法提高了2.31%,种群控制的成熟因子遗传算法进一步提升了7.20%,主要是这两种策略在进化代数较多的情形下,可以缩短最差情况下的搜索时间,从而在可见星可组合得出的较优解比较少时依然可以保持优秀的搜索性能。

3.2 不同数量可见星下的搜索情况

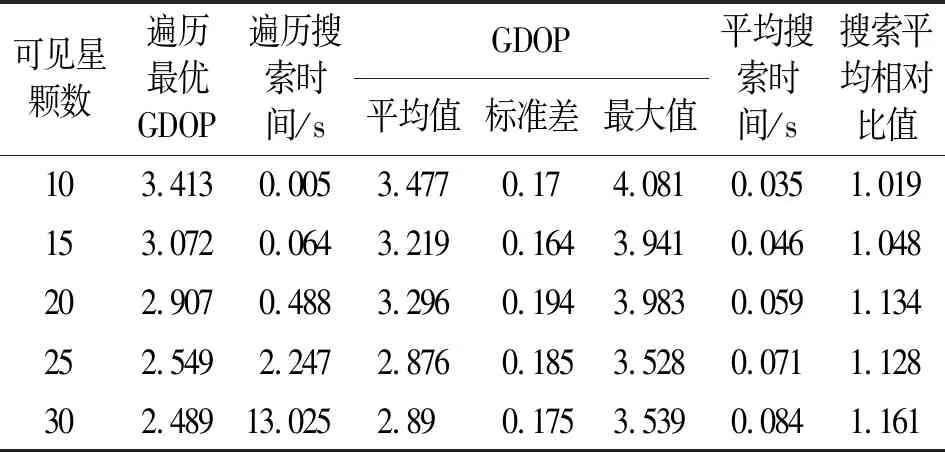
表5 进化20代平均搜索情况Tab.5 Average search for 20 generations of evolution

由表5可见,限定迭代20代条件下,在可见星数量15以上时,本文方法稳定且快于遍历法,各可见星方案下所用时长均小于0.1 s,相对于最优GDOP的差距始终不超过20%,在最差的情况下进化20代GDOP仍然在4以内,根据表1评级仍可达到良。在可见星数量为10时,本文方法性能不足以替代遍历法,这是因为遍历法在10颗星中选取5颗,遍历所需要的次数较少,遗传算法的优势难以彰显,但搜索20代所需的时间并不长,平均GDOP值仅比最优GDOP值大1.86%,虽然最差的情况下GDOP值略大于4,但相较于最优GDOP值也只大20.22%,相对于可见星数15以上时相对搜索精度更高。实际使用时可根据可见星数量多少酌情调整进化代数,以平衡搜索精度和搜索时间。在本文所用星历数据下,在选定时刻和选定测站位置GPS+BDS卫星仰角超过10°的卫星仅有约30颗,因此未对超过30颗可见星的情况下进行搜索。本文所述方法取进化代数20代时在双系统选星的大多数情况下均可满足定位解算需求。

3.3 搜索性能稳定性评估

从图2可看出搜索最优GDOP与进化迭代数具有某种近似指数函数关系。由于每代相对于GDOP的搜索的贡献度不同,推测指数函数的指数部分可能为正态分布,则GDOP或服从对数正态分布。

选取前节可见星为30颗时搜索的最优个体对应的GDOP数据集绘制概率密度图并对GDOP数据进行对数正态分布拟合,如图3所示。图中纵坐标为GDOP取值的概率密度而非GDOP取值的概率,由于概率密度函数在GDOP的数据取值全域积分为1,所以某一有限数值区间的概率密度可以大于1。

图3 可见星30颗20代GDOP概率密度分布情况Fig.3 Probability density distribution of GDOP for 20 generations of evolution at 30 visible satellites

根据图3可见,除去2.8和2.9区间内某一特解概率密度极高外拟合程度较高。上述推测具有一定的参考性。进一步将上节数据都进行对数正态分布拟合,绘制对数正态分布拟合函数汇总,如图4所示。

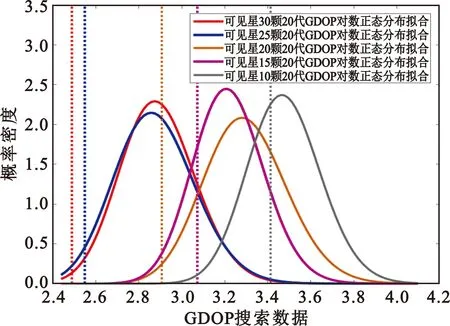
图4 各情况下20代GDOP概率密度分布情况Fig.4 Probability density distribution of GDOP for 20 generations of evolution at for some cases of the number of visible satellites

图4中各情形下的遍历最优GDOP值也用同色点状线标出,可见对于可见星15颗及以下拟合函数的均值已相当接近最优GDOP值,一方面可以印证前文可以适当减少迭代数来进一步减少搜索时间的论断;另一方面也说明当前拟合存在相对较大的失真,由于最优GDOP值左侧数据均为0,导致拟合得出的曲线均值偏右,实际分布优于当前的拟合函数。对于可见星15颗以上的情况,最优GDOP值左侧数据占比较小,分布相对比较符合实际情况,相较于简单统计平均值和标准差,基于拟和分布函数的期望和置信区间更能准确评估当前搜索方案下的获得组合的GDOP值落在的区间。根据拟合分布获得的各情况下期望和3σ置信区间如表6所示。

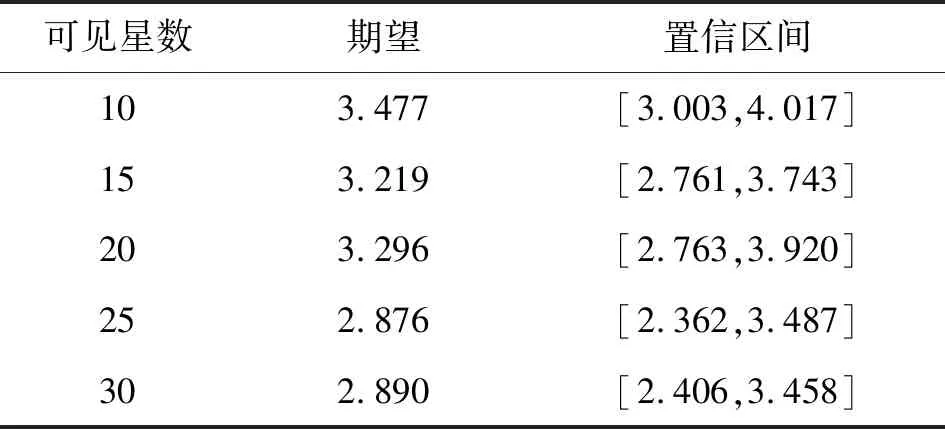
表6 对数正态分布拟合获得的各情况下GDOP均值和置信区间Tab.6 GDOP means and confidence intervals for each case obtained by fitting the lognormal distribution

由表6可以看出,除可见星为10颗之外,剩余情况下GDOP搜索置信区间上限均低于4,由于3σ原则,GDOP搜索值落在区间外的可能性几乎为0,可认为不发生,因此可认为几乎不会出现超过表6所示置信区间上限的情况。基于表5所示最大值虽然高于置信区间上限,但是差距不大,仍然可以印证这一观点(由于进行了10 000次实验,出现超过置信区间上限的最大值是正常的,且拟合本身就存在误差)。拟合实验数据说明本文所述算法具有一定的稳定度,可以进行重复搜索来提高结果的可信度。在应用场景中,由于本文所述方法搜索速度较快,完全可以进行重复选星搜索,取最低GDOP对应的选星组合进行定位解算。

4 结 论

在卫星导航接收机定位解算过程中,为避免传统遍历选星方法需要耗费较长计算时间的问题以及常规遗传选星算法固定高交叉变异概率造成冗余计算的情况,本文提出了引入成熟因子映射的双系统卫星导航接收机选星方法。该方法在保证可接受GDOP的同时,可以有效降低搜索成本。实验结果表明,相较于传统遍历选星算法需要较长搜索时间,该算法的搜索时间大幅缩短,且得出的GDOP可以满足定位需求;相较于常规遗传算法,该方法可以明显减少冗余计算,降低搜索时间。在进化200代的条件下,成熟因子映射遗传算法比固定交叉变异概率的常规遗传算法的搜索时间平均节省约24.75%,引入种群数量控制机制,每代搜索效率有所下降,但搜索时间进一步节省了约55.32%。在可见星15颗以上的情形下,本方法搜索时间稳定优于传统遍历法,各可见星方案下所用时长均小于0.1 s,且相对于最优GDOP的差距始终不超过20%,在大多数情况下,本方法均可胜任选星任务。另一方面,由于遗传算法是随机搜索算法,单次搜索找到最优解的时长是未知的,在极端情况下,可能存在选出的卫星集合的GDOP数值极差或较低门限下解算时间极长的情形,虽然通过概率分布拟合可以认为发生这种概率的可能性极低,但本方法推荐以固定的迭代数为门限,保证每次搜索的时间几乎保持一致,避免由于长时间搜索不到较低门限而无法得出可用的集合。本文从概率密度分布的角度对于搜索的期望进行评估,说明了在重复搜索下的结果期望是稳定的。