导数选择题的常用解题策略

■安徽省阜阳第一中学 赵 慧

在高考试卷中,选择题占有相当大的比例,而有关导数的选择题一般有一定的综合性与深度,对知识与素养要求较高。因此,做好导数选择题对取得高分尤为必要。

解导数选择题的基本原则是准确、迅速。在解答时,应结合导数知识本身的特点,尽量减少书写过程,灵活、快速地得出答案。下面是解导数选择题的常用策略。

一、按部就班,常规处理

例1(2022年新高考Ⅰ卷)(多选)已知函数f(x)=x3-x+1,则( )。

A.f(x)有两个极值点

B.f(x)有三个零点

C.点(0,1)是曲线y=f(x)的对称中心

D.直线y=2x是曲线y=f(x)的切线

对于选项C,验证知f(-x)+f(x)=2成立,于是选项C正确。

令g(x)=x3-x,g(x)是奇函数,关于点(0,0)对称。而y=g(x)的图像向上平移一个单位长度得到y=f(x)的图像,所以y=f(x)关于点(0,1)对称。

令f'(x)=2,得x=±1。当x=1 时,切线为y=2x-1;当x=-1时,切线为y=2x+3。选项D 错误。

故选AC。

评注:大部分选择题会使用此策略。

二、数形结合,直观快捷

例2(2021年新高考Ⅰ卷)若过点(a,b)可以作曲线y=ex的两条切线,则( )。

A.eb＜aB.ea＜b

C.0＜a＜ebD.0＜b＜ea

解 析:如图1,作出函数y=ex的图像。

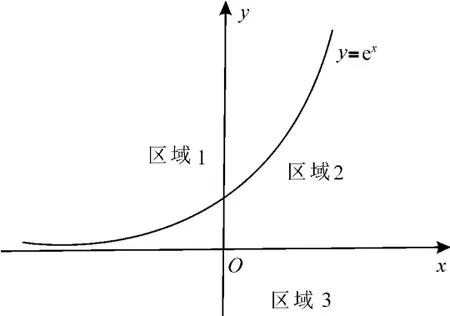
图1

函数y=ex的图像与x轴把坐标平面分成如图1 的三个区域。

当点(a,b)位于区域1时,作不出切线;

当点(a,b)位于区域2 时,可作两条切线;

当点(a,b)位于区域3 时,可作一条切线。

选 D。

评注:此题数形结合明显比常规做法快捷。

三、构造函数,妙用结论

评注:选择题只求结果,不考过程,解题时应用积累的结论可节省时间。

四、选取对数,简化运算

例4若 任 意x,a∈(0,+ ∞),eax+2ab≥a2x,则b的取值范围为( )。

解析:不等式eax+2ab≥a2x,两边取对数得ax+2ab≥lna2+lnx,即ax-lnx+2ba-2lna≥0。

评注:数学中取对数可降低运算级别,达到简化运算的效果。

五、局部入手,先分后合

评注:解题有时需先研究局部,再进行整合,以达到化整为零,各个击破的目的。

六、换元、同构,化难为易

故选B。

例7已知函数f(x)=aex-1-lnx+lna,g(x)=(1-e)x,若ef(x)≥g(x),则a的取值范围为( )。

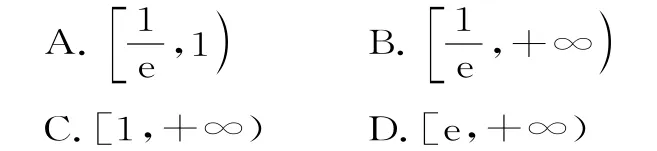
解析:ef(x)≥g(x)可化为ex+lna+e(x+lna)≥elnx+elnx。令φ(x)=ex+ex,即φ(x+lna)≥φ(lnx)。而φ(x)单调递增,所以x+lna≥lnx,即lna≥lnxx。易得h(x)=lnx-x的最大值为-1,于是lna≥-1,解得。故选B。

评注:解题时通过换元,构建同构式,可化繁为简,使问题得到较快解决。