二项式定理中的赋值技巧
2024-03-26河南省许昌市建安区第一高级中学丁书珍
■河南省许昌市建安区第一高级中学 丁书珍
■河南省鄢陵县第二高级中学 刘俊霞
在二项式定理的求值问题中,尤其是求解二项展开式的系数和等问题时,我们常常采用赋值法求解。即对二项展开式中的相关字母进行赋值,进而得以求解二项式系数及与之相关的综合问题,在选择性必修三课本中就给出了用法,让我们走进课本,从课本入手,了解赋值法在二项式定理中的应用,以便同学们正确掌握二项式定理中的赋值技巧。
已知(1+x)n=C0n+C1nx+C2nx2+…+,令x=1,得 2n=Cn0+Cn1+Cn2+…+Cnn。
这就是说, (a+b)n的展开式的各二项式系数的和等于 2n。
例1求证:在(a+b)n的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和。
解析:奇数项的二项式系数的和为C0n+C2n+C4n+…;
偶数项的二项式系数的和为C1n+C3n+C5n+…。
由于(a+b)n= C0nan+ C1nan-1b+中的a,b可以取任意实数,因此我们可以通过对a,b适当赋值来得到上述两个系数和。
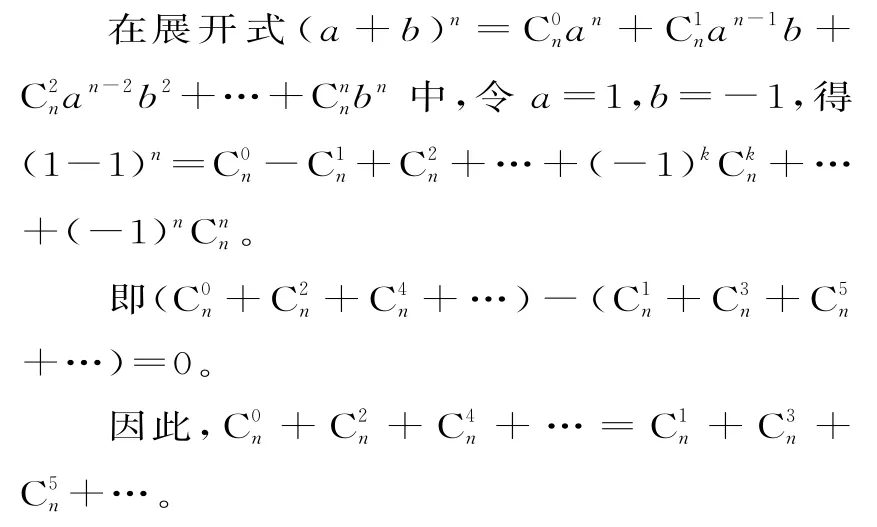
故在(a+b)n的展开式中,奇数项的二项式系数之和等于偶数项的二项式系数之和。
点评:实际上,a,b既可以取实数,也可以取多项式。我们可以根据具体问题的需要灵活选取a,b的值。
例2已知(3x-1)8=a8x8+a7x7+…+a1x+a0,求下列各式的值:
(1)a8+a7+…+a1+a0;
(2)|a8|+|a7|+|a6|+…+|a0|;
(3)a1+a3+a5+a7。
解析:(1)令x=1,得a8+a7+…+a1+a0=(3-1)8=28=256。
(2)因为|a8|+|a7|+|a6|+…+|a0|=a8-a7+…-a1+a0,所以令x=-1,得:
|a8|+|a7|+|a6|+…+|a0|=a8-a7+…-a1+a0=(-3-1)8=48=65 536。
(3)由(1)和(2)知:
点评:赋值法是求二项展开式系数和及有关问题的常用方法,注意取值要有利于问题的解决,可以取一个值或几个值,也可以取几组值,解决问题时要避免漏项。同时,要注意问题的实质及变形,如求各项系数的绝对值的和时,要先根据绝对值里面数的符号赋值求解。同时注意这类问题的变形写法,如:|a8|+|a7|+|a6|+…+|a0|=a8-a7+…-a1+a0=(a8+a6+a4+…)-(a7+a5+a3+…)等。对于比较繁杂式子的求值问题,要先观察式子的特点,结合所学知识如因式分解等,对式子进行因式分解,再赋值求解。

例4已知(2x+1)n=a0+a1x+a2x2+…+anxn的展开式中的各项系数和为243,求a1+2a2+3a3+…+nan值。
解析:令x=1,可得a0+a1+a2+a3+a4+…+an=3n=243。
解得n=5。
对(2x+1)n=a0+a1x+a2x2+…+anxn求导,可得:
2n(2x+1)n-1=a1+2a2x+3a3x2+…+nanxn-1。
令x=1,可得:
a1+2a2+3a3+…+nan=2n·3n-1=2×5×34=810。
点评:观察问题中的式子,我们发现,an前面的系数是原式xn的幂指数,先借助于求导可以实现数由指数位置向系数位置的转化,再对求导所得结果赋值即可得到该类型题的答案。
例5(1) 若(1+mx)6=a0+a1x+a2x2+…+a6x6,且a0+a1+a2+…+a6=64,则求实数m的值。
(2)已知C4n=C6n,设(3x-4)n=a0+a1(x-1)+a2(x-1)2+…+an(x-1)n,求a1+a2+…+an。
解析:(1)令x=1,可得(1+m)6=a0+a1+a2+…+a6=64。
则1+m=2或1+m=-2。
解得m=1或m=-3。
(2)因为C4n=C6n,所以n=10。
则(3x-4)10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10。
令x-1=0,即x=1,可得a0=(3-4)10=1。
令x-1=1,即x=2,可得a0+a1+a2+…+a10=(6-4)10=210。
故a1+a2+…+a10=210-1。
点评:在与二项式定理有关的赋值求值问题中,首先要观察需要求值问题与原题中条件之间的关系,从展开式入手,通过比较,正确找出需要赋的值,才能求出正确的答案。
