计数原理单元测试卷(A 卷)
2024-03-26河南省郑州实验高中曲海胜
■河南省郑州实验高中 曲海胜
一、单选题(本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.从4名男生与3名女生中选2人去参加一场数学竞赛,则男女生各1 人的不同的选派方法数为( )。
A.7 B.12 C.18 D.24
2.2023年夏天贵州榕江的村超联赛火爆全国,吸引了国内众多业余球队参赛。现有6 个参赛队伍代表站成一排照相,其中贵阳折耳根队与柳州螺蛳粉队必须相邻,同时南昌拌粉队与温江烤肉队不能相邻,那么不同的站法共有( )种。
A.144 B.72 C.36 D.24
A.14 B.15 C.13 D.12
4.北斗七星是夜空中的七颗亮星,我国汉代纬书《春秋运斗枢》就有记载,它们组成的图形像我国古代舀酒的斗,故命名北斗七星。北斗七星不仅是天上的星象,也是古人藉以判断季节的依据之一。如图1 所示,用点A,B,C,D,E,F,G表示某一时期的北斗七星,其中B,D,E,F看作共线,其他任何3个点均不共线,过这7个点中任意2个点作直线,所得直线的条数为( )。

图1
A.4 B.13 C.15 D.16
5.如图2所示,古代中国的太极八卦图是以同圆内的圆心为界,画出形状相同的两个阴阳鱼,阳鱼的头部有个阴眼,阴鱼的头部有个阳眼,表示万物都在相互转化,互相渗透,阴中有阳,阳中有阴,阴阳相合,相生相克,蕴含现代哲学中的矛盾对立统一规律。由八卦模型图可抽象得到正八边形,从该正八边形的8个顶点中任意取出4个构成四边形,其中梯形的个数为( )。

图2
A.16 B.20 C.24 D.28
A.-20 B.5 C.15 D.35
7.某学校派出5名教师去3所乡村学校支教,其中有一对教师夫妇参与支教活动。根据相关要求,每位教师只能去1 所学校参与支教,并且每所学校至少有1 名教师参与支教,同时要求这对教师夫妇必须去同所学校支教,则不同的安排方案有( )。
A.18种 B.24种
C.36种 D.48种
8.中国南北朝时期的著作《孙子算经》中,对同余除法有较深的研究,设a,b,m(m>0)均为整数,若a和b被m除得的余数相同,则称a和b对模m同余,记为a≡b(modm)。如9 和21 被6 除 得 的 余 数 都 是3,则记9≡21(mod6)。若a≡b(mod10),且,则b的值可以是( )。
A.2 019 B.2 020
C.2 021 D.2 022
二、多选题(本题共4小题,每小题5分,共20分。在每小题给出的选项中,有多项符合题目要求。全部选对的得5 分,部分选对的得2分,有选错的得0分。)
9.下列结论正确的是( )。

11.2021年7月24日,中共中央办公厅、国务院办公厅印发《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,要求各地区各部门结合实际认真贯彻落实。同年8月,国务院教育督导委员会办公室印发专门通知,拟对各省“双减”工作落实进度每半月通报一次。2021 年10 月,全国人大表示:“双减”拟明确入法,避免加重义务教育阶段学生负担。2021年11月3日,市场监管总局等八部门发布《关于做好校外培训广告管控的通知》,坚决杜绝地铁、公交站台等所属广告牌、广告位刊发校外培训广告。在“双减”政策的推动下,某市教育局提出了教师轮岗制度,让更多的学生享受到更好、更优质的师资,充分体现教育的公平性。现从该市某中学调8名不同科目的教师到另一所中学的4个不同班级任教,要求每个班级至少分配1名教师,至多分配3名教师,则( )。
B.有2个班级分配1 名教师,另2 个班级分配3名教师,有种分配方法
C.根据班级实际情况,(1)班需要1名教师,(2)班和(3)班均需要2名教师,(4)班需要3名教师,则有种分配方法
D.根据教学经验分析,甲、乙、丙3 名教师分配到1 个班级才可达到教学效果最优,则有种分配方法
12.在某城市中,A,B两地之间有如图3所示的道路网,甲随机沿道路网选择一条最短路径,从A地出发到B地,则下列结论正确的是( )。
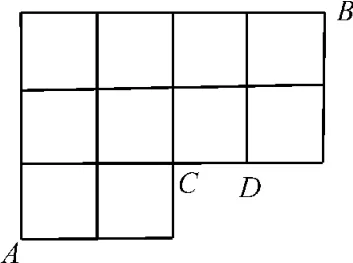
图3
A.不同的路径共有31条
B.不同的路径共有41条
C.若甲途经C地,则不同的路径共有18条
D.若甲途经C地,且不经过D地,则不同的路径共有8条
三、填空题(本题共4小题,每小题5分,共20分。)
13.已知(1-x)9+m(x+1)10=a0+a1x+a2x2+…+a9x9+a10x10,若a9=a10,则a2=_____。
14.若(1-ax+x2)4的展开式中x5的系数为-56,则实数a=____。
16.已知a,b∈{-1,0,2,3},则关于x的方程ax2+2x+b=0有实数解的有序数对(a,b)的个数为_____。
四、解答题(本题共6 小题,共70 分,解答时应写出文字说明、证明过程或演算步骤。)
17.(本小题10 分)电影《志愿军雄兵出击》讲述了在极其简陋的装备和极寒严酷环境下,中国人民志愿军凭着钢铁意志和英勇无畏的精神取得入朝作战第一阶段战役的胜利,著名的“松骨峰战斗”在该电影中就有场景。现有3名男生和4名女生相约一起去观看该影片,他们的座位在同一排且连在一起。
(1)女生必须坐在一起的坐法有多少种?
(2)女生互不相邻的坐法有多少种?
(3)甲、乙两位同学相邻且都不与丙同学相邻的坐法有多少种? (列出算式,并计算出结果)
18.(本小题12分)(1)解关于x的不等式Ax8<6Ax-28。
19.(本小题12分)已知集合A={x|1<log2x<3,x∈N*},B={4,5,6,7,8}。
(1)从A∪B中取出3 个不同的元素组成三位数,则可以组成多少个?
(2)从集合A中取出1 个元素,从集合B中取出3个元素,可以组成多少个无重复数字且比4 000大的正整数?
(1)求n和a的值。
(2)展开式中是否存在常数项? 若存在,求出常数项;若不存在,请说明理由。
21.(本小题12分)用1,2,3,4,5,6这6个数字,可以组成多少个无重复数字的:
(1)四位偶数?
(2)数字1、3、5互不相邻的六位数?
(3)六位数? 其中数字6、4、1 按自左至右的顺序保持不变(如634 512,562 431)。
注:所有结果均用数值表示。
22.(本小题12分)已知(a-2x)8=a0+a1(x-1)+a2(x-1)2+…+a8(x-1)8,其中实数a>0,且x2的系数为81 648。
(1)求实数a的值。
(2)计算:(ⅰ)(a0+a2+a4+a6+a8)·(a1+a3+a5+a7);
(ⅱ)|a0|+|a1|+|a2|+…+|a8|。(结果用幂的形式表示)
