膜圆顶及塔架对南极望远镜风载影响的仿真分析*

任志敏 温海焜 李国平 王 圣 赵秀勇

(1 中国科学院南京天文光学技术研究所 南京 210042)

(2 中国科学院天文光学技术重点实验室(南京天文光学技术研究所) 南京 210042)

(3 中国科学院大学 北京 100049)

(4 国家能源集团科学技术研究院有限公司 南京 210023)

1 引言

南极大陆被证实是地球上最好的天文台址,其中,位于南极大陆最高点的Dome A地区具有独特的天文观测条件: 超长的极夜时间(每年的冬季超过4个月)、低风速(通常低于10 m · s-1)、低温干燥(冬季温度在-70°C--60°C之间且夏季温度低于-40°C;冬季的相对湿度在25%到45%之间)[1]、极好的视宁度条件(夜间视宁度中值为0.31′′,最低能够达到0.13′′)、极薄的大气边界层(边界层中值为13.9 m)[2-4].上述这些特点使得Dome A成为绝佳的天文观测台址.

为了充分利用Dome A的天文观测优势,可以利用塔架将望远镜安装在大气边界层上方,采用对望远镜观测影响极小的天文圆顶,隔绝热源对观测环境的影响并减小望远镜附近的风速以避免风载造成的望远镜振动与镜面变形.综上,我们可以考虑以下方案: (1)将望远镜安装在高于Dome A大气边界层的塔架之上;(2)使用轻质膜结构圆顶.由于轻质膜圆顶为完全开放式的结构,而且钢与膜的组合结构有轻便、吸热量小的特点,所以圆顶视宁度极佳[5].此外,该类圆顶的整体质量和单个零件尺寸均很小,容易满足Dome A运输和安装的要求;(3)用保温材料将散热结构(电机、塔架等)包裹进行隔热处理[6];(4)采用风屏结构以减小望远镜周围的风速和湍流[7].

计算流体力学(Computational Fluid Dynamics,CFD)在望远镜的风载分析中得到了广泛的应用.De 乙oung等[8]对Gemini望远镜圆顶内的气体流动进行了数值模拟,指出湍流随风环境和随动圆顶的开口方向变化而发生相应的改变;三十米望远镜(Thirty Meter Telescope,TMT)项目组[9]采用CFD的方法对TMT工作过程受到的外流场进行了模拟仿真,将模拟的风载数据导入望远镜集成模型中,从而对望远镜的结构进行了优化;中国科学院南京天文光学技术研究所的徐江海等[10]利用CFD分析了经典形式的球形、柱形、蚌壳折叠式圆顶在风载作用下对风速及湍动能的影响;中国科学院光电技术研究所的潘年[11]分析了圆柱形开放式圆顶在风载下的风速及湍动能的分布,同时将CFD分析结果与Gemini望远镜的实测结果进行了对比,证明了CFD分析的可靠性.

本文对望远镜、圆顶及塔架进行了建模,利用CFD进行数值模拟分析,当圆顶完全打开时,在给定风速和温度等条件下,分析了不同风向角(α)、方位轴转动角(β)及镜筒转动角(γ)时,望远镜周围的风速、湍动能(Turbulence Kinetic Energy,TKE)、光程差(Pv)等信息,并且研究了风屏对望远镜周围温度及光程差的影响.旨在用数值方法评价风载对望远镜周围光学传输环境的分布特性.

2 数值仿真原理

2.1 湍流模型的数学描述

本文采用标准k-ε湍流模型,这种模型有着计算稳定,好的经济性和高计算精确度的优点[12].其输运方程为:

式中k为湍动能、ε为湍流动能耗散率、ρ为流体密度、t为时间、µ为动力粘度、µt为湍流粘度、ui为流速、xi和xj为相互垂直的两坐标轴、σk和σε为湍流动能k和耗散率ε对应的普朗特数(分别取为1和1.3)、Gk为由平均速度梯度引起的k的产生项、C1ε和为经验常数(分别取为1.44和1.92).

2.2 湍流对光程差的影响

大气温度和速度场的不均匀形成了大气湍流,湍流会造成流场的密度及折射系数随时间的不均匀变化.从光波波前的角度分析大气湍流对望远镜成像质量的影响可以分为以下两种: 第1种是像运动与像模糊,主要表现为波前倾斜造成的像点围绕着“平均位置”不规则的抖动,以及位相畸变带来的不同像点位移的距离不同;第2种是像的闪烁,是对数振幅涨落造成的成像强度的变化[13].

湍动能是湍流速度脉动的度量,其大小直接关系到流体内部动量、热量和水汽的输运.湍动能定义为:

湍动能从大尺度涡旋向小尺度涡旋传递,部分湍动能在各级旋涡转为流体热能,进而导致大气温度起伏.折射率随介质的密度和成分而变化,大气折射率场的结构是由温度场、湿度场和压力场的结构决定的,在空气中可以用柯西-劳伦斯公式表示为[14]:

式中N为空气折射率;T为绝对温度,单位为K;λ为光的波长,单位为µm;P为干燥的大气压强,e为水汽的压强,单位均为hPa.

光波通过湍流介质的光程公式为:

式中L为光在介质中传播的几何路程,u、v、w为笛卡尔坐标系的3个方向.由(3)式可知,折射率的变化取决于环境温度,大气压强和水汽含量.Dome A的空气湿度非常低,同时压力的波动对折射率的影响也可以忽略不计,折射率主要受湍流动能带来的温度波动的影响[14].由(4)式可知,折射率的变化会导致光束的光程差异变大,使来自天体的星光波前畸变,即光强和相位发生改变,导致成像图像发生模糊、抖动、平移等现象[15].图1表示了湍动能对视宁度的影响途径.

图1 湍动能对视宁度的影响(θdome为圆顶视宁度,ΔTc-a为圆顶内外的温度差)Fig.1 Effect of TKE on seeing (θdome is the seeing degree of the dome,ΔTc-a is the temperature difference inside and outside the dome)

3 数值仿真

3.1 计算模型

望远镜的研制需要经历概念设计、详细设计、加工与检测、外场建设、集成和调试等阶段.对于方案制定的概念设计阶段,望远镜的详细结构以及台址周边环境的具体情况尚未明确.鉴于这些不确定性,在研究风载对望远镜的影响时,本文对望远镜、圆顶、塔架以及外部环境做出了适当的简化.仿真望远镜为口径2.5 m的地平式望远镜.轻质圆顶的直径为12 m,两侧为驱动电机,圆顶保持完全打开的状态时高度为0.42 m.塔架包含圆顶塔架和望远镜塔架两部分,其中内侧的望远镜塔架为倾角7°向上收缩的正六边形结构,分为3层结构,每层的侧面都由交错的斜杆构成,塔架底边边长为4.3 m,高度为10.7 m;外侧的圆顶塔架为倾角10°向上收缩的四边形结构,分为两层结构,每层的侧面都由交错的斜杆构成,塔架底边边长为17.2 m,高度为15 m;两个塔架每个杆件的截面尺寸均为0.2 m×0.2 m.仿真模型的整体结构如图2所示.通过改变风向角(α)-方位轴转动角(β)-镜筒转动角(γ)的组合(为表述方便,文中形如0-0-120代表模型处于风向角0°、方位角0°、高度角120°的位置)实现模型在不同运行位置时受风载变化的仿真模拟.

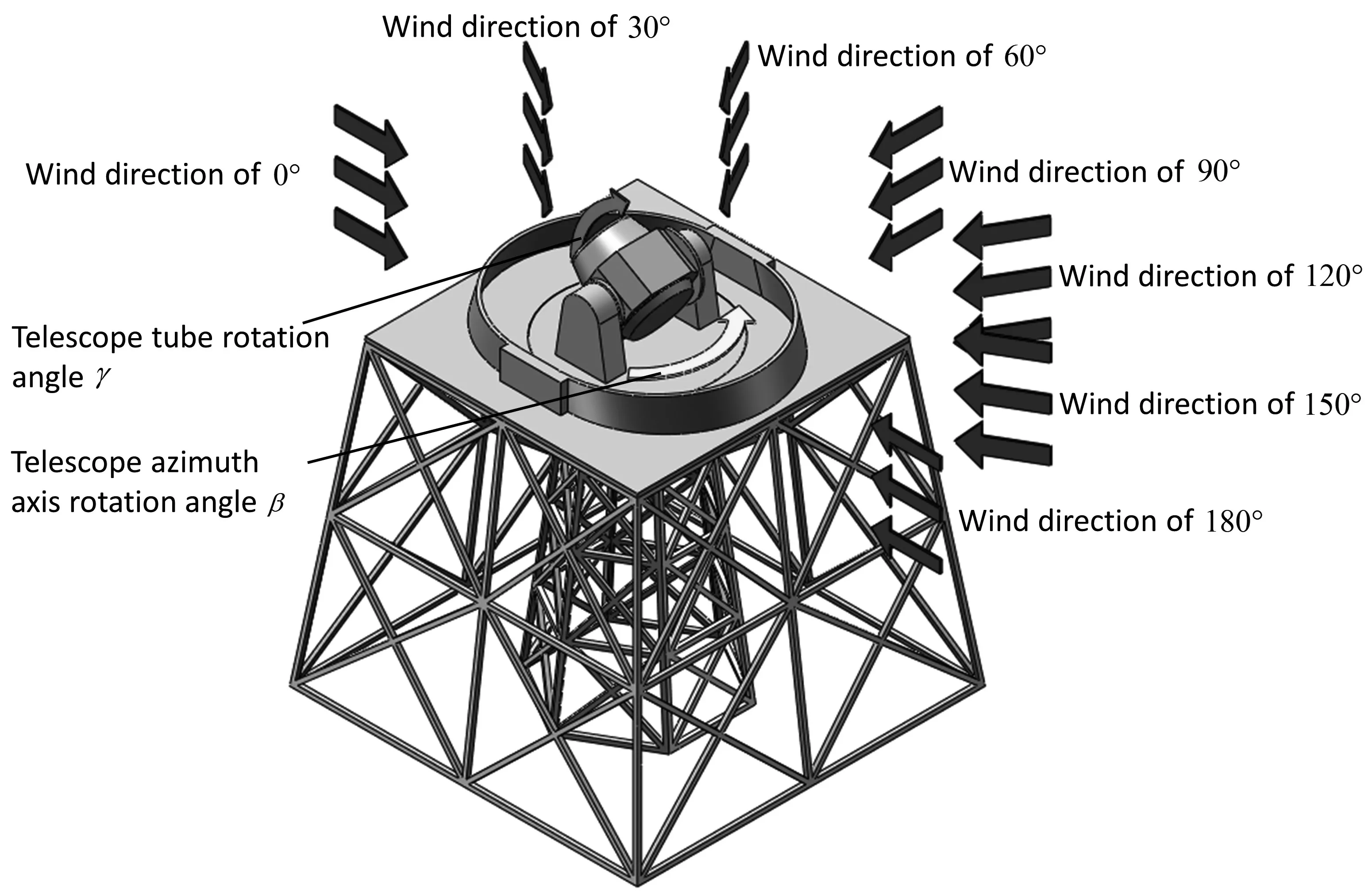
图2 仿真模型结构图(图中的风向角-方位轴转动角-镜筒转动角为0-0-30,风向初始角度与塔架侧面垂直,方位轴初始角度与风向初始角度同向,镜筒转动角为望远镜观测方向与水平面的夹角,图中的箭头表示风向角、方位轴转动方向和镜筒转动方向)Fig.2 Three-dimensional (3D) model of telescope and accessory equipment (In the figure,the wind direction angle-azimuth axis rotation angle-lens tube rotation angle is 0-0-30.The initial angle of the wind direction is perpendicular to the side of the tower,and the initial angle of the azimuth axis is in the same direction as the initial angle of the wind direction.The rotation angle of the lens tube is the angle between the observation direction of the telescope and the horizontal plane.The arrows in the figure indicate the wind direction angle,the rotation direction of the azimuth axis and the rotation direction of the lens tube)

3.2 边界条件

通常,望远镜的工作上限风速为10 m·s-1,所以设置地面15 m高处为10 m·s-1的入口风速以得到极限工作情况下2.5 m望远镜周围的流场分布情况,其他不同高度的入口风速值按照Dome A风速分布(5)式[16]设置;同时取Dome A的平均温度213.15 K及大气压强0.5358 atm作为仿真流体域的环境温度及压强;设置空气为不可压缩理想气体;出口为自由流出边界;圆顶、望远镜和塔架设定为粗糙度0.5、无滑移的壁面;流场的其他壁面设置为可滑移的壁面.

3.3 网格划分

为了提高计算效率、计算收敛性和计算速度,在模拟中采用了分区域划分网格的方法,在远离分析目标的流体域采用平均网格尺寸为100 mm的六面体网格,在分析目标周围流场参数梯度变化较大的区域将网格加密为平均尺寸为50 mm的四面体网格,对分析目标表面进一步加密为平均尺寸25 mm的四面体网格,整个计算区域的网格数在各仿真条件下均不少于340万,网格的划分情况如图3所示.

图3 部分流体域的网格划分Fig.3 Meshing of partial fluid domains

3.4 计算结果

3.4.1 风速分析

对风向角(α)分别为0°、30°、60°、90°(120°、150°、180°与60°、30°、0°风向角完全对称)时,不同β和γ对应的2.5 m望远镜周围稳态风速分布进行分析.由于望远镜镜筒附近以及观测方向的风速分布会影响到望远镜的观测,所以本文在进行分析时主要考虑镜筒观测方向10 m内以及镜筒周围5 m内的风速分布.

首先分析α对稳态风速分布的影响,如图4所示,当γ相同时,只要任意两组的α-β值相同,则两组间的速度云图分布也相同,由此可认为塔架和膜圆顶周围的风速分布对α的改变不敏感,α=30°、60°、90°时的镜前风速分布规律均可以由α=0°时的分布结果来表示.为了直观地表示镜筒观测方向的风速分布,图中云图平面均垂直于地面和望远镜镜面且过镜面的中心点.

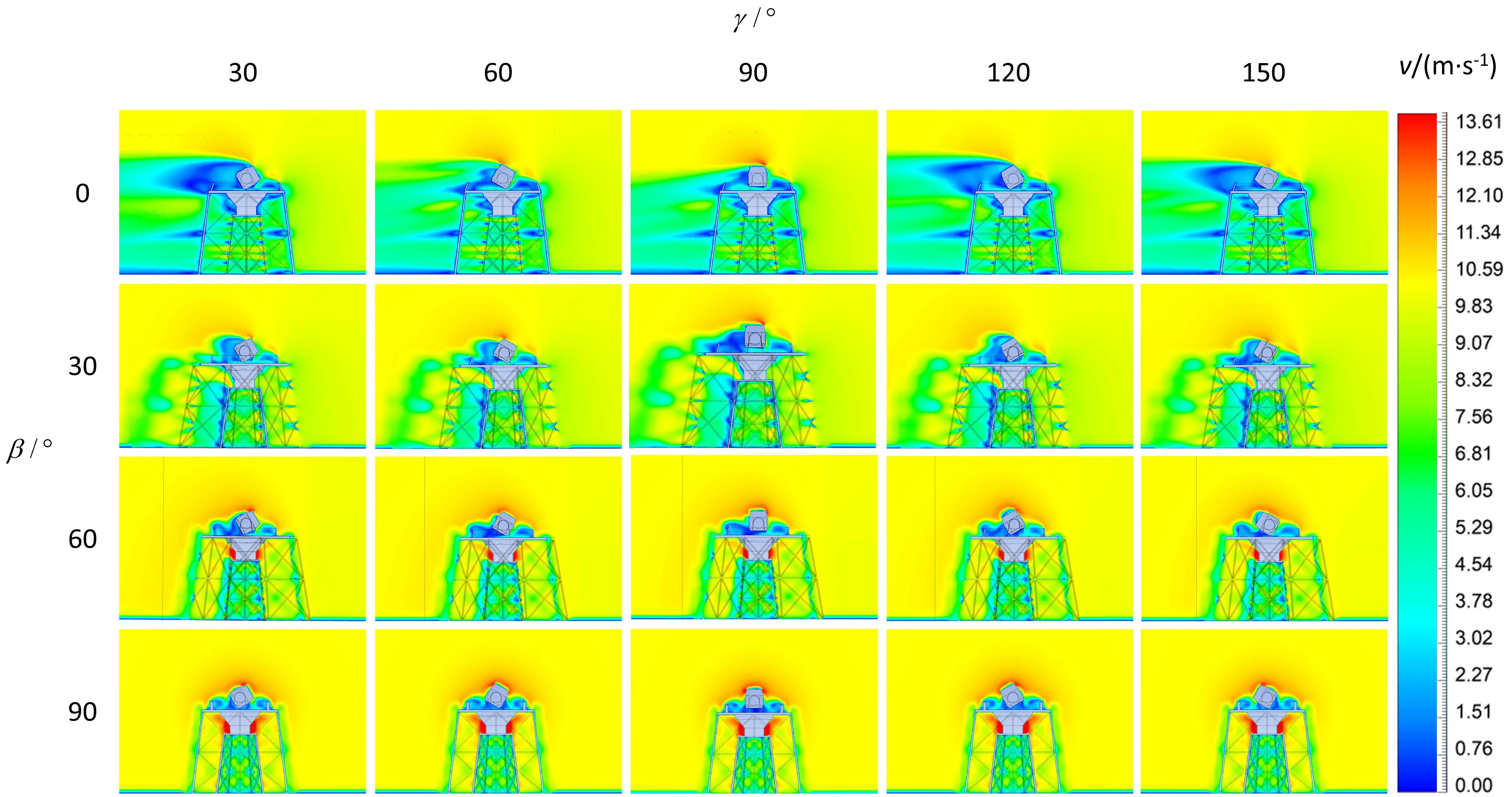
图4 α=0°时2.5 m望远镜周围稳态风速分布云图Fig.4 Cloud map of steady-state wind speed distribution around 2.5 m telescope at α=0°

对图4做横向对比分析.当β=0°、30°、60°时,随着γ逐渐增大镜筒观测方向越来越背离来流方向,所以镜面前方的风速有显著的减小,镜面所受风载也会减小[17];但γ的逐渐增大导致镜面前方的风速分布出现明显的分层结构,风速的分层会导致空气结构的分层,空气的折射率在风速的突变层间产生较大的变化,从而影响光线的稳定传播.当β=90°时,由于镜面与风向的角度始终为90°,所以镜筒观测方向的风速分布在各γ均一致,均是在镜面处有明显的风速分层结构.

做纵向对比分析.在γ分别为30°、60°、90°、120°、150°时,2.5 m望远镜周围的风速分布均随着β的增大而增大,镜面前方的风速分层越来越紧密且逐渐贴近镜面.风向来流与镜面的角度逐渐增大,镜面所受的风作用力变小,镜面的变形会减小.

为了定量分析光路上的风速变化情况,本文按照图5的排布方式取垂直于镜面的25条长度为10 m的光路,每条光路上均匀取1000个采样点进行采样,图6为风速分布采样图.

图5 垂直于镜面采样线的位置及编号Fig.5 Position and number of the sample line perpendicular to the mirror

图6 α=0°时垂直于镜面方向的风速分布Fig.6 The wind speed distribution perpendicular to the mirror in the case of α=0°

对图6分析得到,当镜面处于迎风(γ＜90°)状态时,同一组内25条取样线上发生风速波动的空间范围一致,但镜面边缘取样线(6、8、10、12、14-25)和镜面内侧取样线(1、2、3、4、5、7、9、11、13)分别呈现两种不同的变化趋势.各取样线上的风速值均在离镜面约2 m的范围内发生剧烈的变化,并且在2 m后逐渐趋于稳定风速值10 m·s-1.镜面边缘取样线(6、8、10、12、14-25)的波动变化趋势为由镜面的0 m · s-1迅速增大,然后在离镜面0.3 m远处出现一个明显的风速拐点,此后风速的变化变得缓和;镜面内侧取样线(1、2、3、4、5、7、9、11、13)的波动变化趋势为由镜面的0 m·s-1较平稳地增加到10 m·s-1.此外,γ越大风速值的变化范围越大,在0-0-30时,风速值的变化范围仅为0-10.5 m·s-1,在0-90-90时,风速的变化范围可达到0-13.9 m·s-1.

当镜面处于背风(γ＞90°)状态时,同一组内25条取样线上的风速波动范围和变化趋势一致,每条取样线上的风速值均是从镜面处的0 m·s-1迅速增大到2-4 m·s-1,随后下降到0.5-1.5 m·s-1,之后迅速增大到最大风速值后缓慢归于一个稳定的风速值.但各取样线上发生风速波动的空间范围则随着镜面的背风程度(γ)的增大而增大,在0-60-120时,25条取样线上的速度波动发生在离镜面3 m的范围内,在0-30-150时,各取样线上的速度波动则直到离镜面6 m处才逐渐平缓.

此外,在所有来流风与镜面平行的情况下,镜面前方的气流变化规律均相似,由镜面处的0 m·s-1增加到离镜面0.3 m处的14 m · s-1,然后缓慢变化到稳定风速10 m · s-1.总体而言,在迎风状态下,镜面前方的空气流速变化更加稳定,发生变化的空间范围也更小,所以镜面前方空气的状态更为均匀、光线的传输更加稳定.背风状态下,镜面前方的空气流速变化较不稳定,空气密度的均匀性也必然较差,从而影响到光程差的大小.本文尝试使用风屏结构缓和这种剧烈的风速变化,改善望远镜周围的风速分布环境.

3.4.2 湍动能分析

对α分别为0°、30°、60°、90°时,不同β和γ对应的2.5 m望远镜周围的TKE分布进行分析.由于望远镜镜筒附近以及观测方向的湍动能分布会影响到望远镜的观测,所以本文在进行分析时主要考虑镜筒观测方向10 m内以及镜筒周围5 m内的湍动能分布.

首先分析α对湍动能分布的影响,如图7所示,与速度分布规律类似,当γ相同时,只要任意两组间的α-β值相同,则两组的湍动能云图分布相同,由此可以认为塔架和圆顶周围的湍动能分布对来流风向(α)的改变不敏感,α=0°、60°、90°时镜前湍动能分布规律均可以由α=0°时的分布结果来表示.为了直观地表示镜筒观测方向的湍动能分布,图中云图平面均垂直于地面和望远镜镜面且过镜面的中心点.

然后对图7做横向对比分析.当β=0°、30°、60°时,随着γ逐渐增大镜筒观测方向的湍动能数值和分布范围逐渐增大,导致环境温度变得更不均匀、空气折射率的不均匀使光程差变大.当β=90°时,由于镜筒与风向的角度始终为90°,所以镜筒观测方向的湍动能分布在各γ均一致,均是在镜面表面有薄薄一层湍动能稍大的区域.

最后对图7做纵向对比分析.当γ=30°、60°时,不同β下镜面前方的湍动能分布差异不大,均是镜面表面有薄薄一层湍动能值较小的区域;当γ=90°时,随着β的增大,湍动能的数值有所减小,但是湍动能均集中分布在镜面附近没有变化;当γ=120°、150°时,随着β的增大,望远镜观测方向的湍动能分布越来越紧密且逐渐贴近镜面.

同样,对光路方向的湍动能做定量分析,每条取样线上的湍动能分布如图8所示.

图8 α=0°时垂直于镜面方向的湍动能分布Fig.8 TKE distribution perpendicular to the mirror direction at α=0°

对图8分析得到,当镜面处于迎风(γ＜90°)的状态时,不同γ取值下各组25条取样线上发生TKE波动的范围与趋势均一致,每条取样线上的湍动能值均在离镜面约2 m的范围内发生剧烈的变化,并且在2 m后逐渐趋于0;波动变化趋势均为从镜面表面到离镜面0.2 m的范围内由接近0值迅速增大到最大值,然后在离镜面2 m的范围内迅速降到很小的值,之后则会缓慢趋于稳定.迎风状态下各组的湍动能值均比较小,在0-0-60湍动能的最大值仅为约0.2 J·kg-1.

当镜面处于背风(γ＞90°)状态时,每组25条取样线上的湍动能波动趋势在不同γ取值下均一致,由镜面处大于0的值逐渐增大到最大值,之后随着远离镜面逐渐归于0值;但各取样线发生湍动能变化的空间范围则随着镜面的背风程度(γ)的增大而增大.在0-0-120时,各取样线上的湍动能波动发生在离镜面4 m的范围内,在0-0-150时,各取样线上的湍动能波动则直到离镜面8.5 m处才逐渐平缓.此外,湍动能值波动范围随着背风程度的增大而略有减小.背风状态下各组的湍动能值均比较大,在0-60-120时,湍动能的最大值达到13.5 J·kg-1.

3.4.3 光程差分析

由于光程的大小受空气折射率的影响,空气折射率又由湍动能造成的温度变化决定,不同的湍动能分布就代表着不同的光程差,由前文分析得到α=30°、60°、90°的湍动能分布情况可由α=0°来表示,所以在此只分析α=0°时,最大光程差Pv随β,γ值的变化关系.

由(3)-(4)式可得到不同β、γ时各组取样光线所经过的实际光程S1、S2、...、S25,然后可以求出最大光程差Pv=Smax-Smin.图9为β=0°、30°、60°、90°时Pv随γ值变化的情况.

图9 β=0°、30°、60°、90°时Pv随γ的变化Fig.9 Change of Pv with γ at β=0°,30°,60°,90°

β取不同值时曲线的变化趋势相同,均是随着γ的增大Pv先缓慢减小,在γ=90°时达到最小值,然后再逐渐增大,并在γ=150°时达到最大值.整体来看,β值越小光程差越大,最大的光程差为0-0-150时的229.4 nm;β=90°时光程差的变化幅度不大且数值较小,最小为0-90-60时的24 nm.

3.4.4 风屏对湍流的改善作用研究

在望远镜周围安装风屏可以有效减少望远镜附近风速突变及湍动能,但同时也会造成一定程度的温升[7].本文研究了风屏对2.5 m望远镜周围风速、湍动能及温度的影响.由于Dome A地区没有固定的主风向,所以将风屏模型简化成360°围绕圆顶塔架顶端外侧均匀排布的矩形长杆,每根杆的尺寸均为0.1 m×0.1 m×4.2 m,杆与杆的间距为0.05 m,杆的高度略低于望远镜观测时镜筒的最大高度,如图10所示.

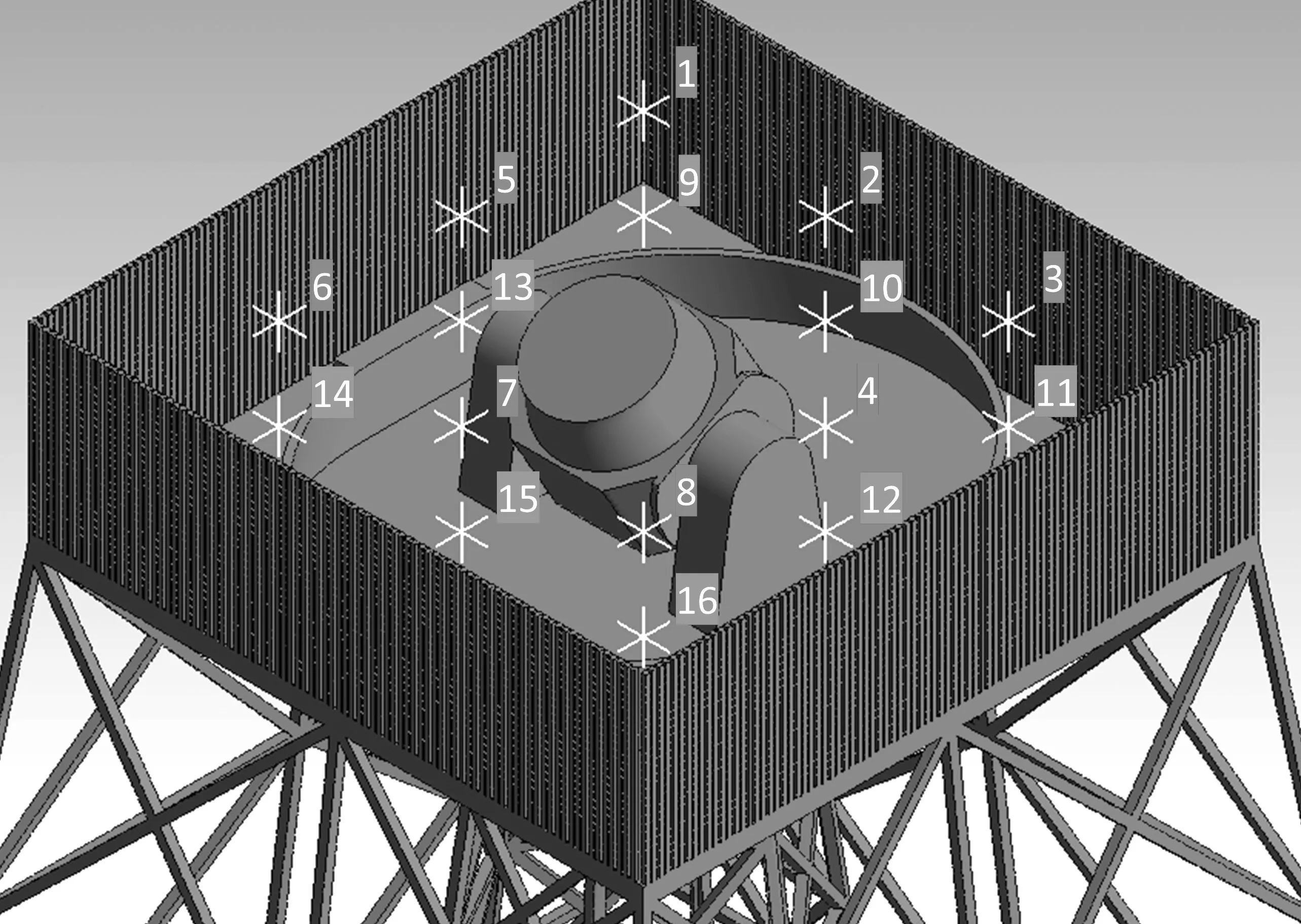
图10 望远镜周围风屏的结构及温度采样点Fig.10 Structure of the wind screen around the telescope and temperature sampling points

图11和图12分别为α=0°时,不同β、γ对应的湍动能和风速分布情况,为了直观地表示镜筒观测方向的湍动能和风速分布,图中云图平面均垂直于地面且平行于望远镜观测方向.由图11分析得到在不同β、γ时,2.5 m望远镜观测方向与远处自由稳定大气的湍动能值差别不大,均为略大于0的数值.从图12可以得到在不同β、γ时,高速风在通过风屏后,风速有大幅度减小,同时由于膜圆顶对风的进一步阻挡作用,望远镜周围的风速值＜1 m·s-1,望远镜所受风载显著降低.

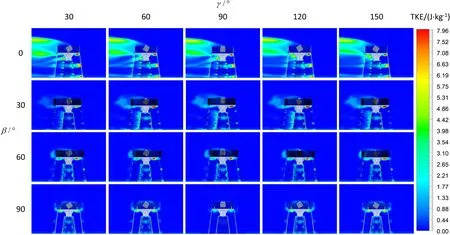
图11 加装风屏后α=0°时望远镜和圆顶及塔架周围的湍动能云图Fig.11 TKE cloud map around the telescope,dome and tower at α=0° after installing the wind screen

图12 加装风屏后α=0°时望远镜和圆顶及塔架周围的风速云图Fig.12 Cloud map of wind speed around the telescope,dome and tower at α=0° after installing the wind screen

为了定量研究风屏带来的温升效应,对望远镜周围16个点的温度值进行采样分析,图10为采样点的分布情况,表1为采样点的温度.

表1中的数据并没有显示出望远镜周围的温度有特别的分布趋势与规律性.但是,16个采样点的最高温度为213.196 K,比环境温度213.150 K高0.046 K;平均温度TA为213.194 K,较环境温度高0.044 K.仿真关于风速、湍动能、温度的结果与文献[7]中得到的10 m·s-1的风速在通过风屏后最大温升不大于0.050 K,风速在离风屏1 m远、3 m高的位置处降为来流风速的1/3至1/4的结论一致.

同时对受风屏影响的最大光程差进行了分析,虽然湍动能的数值较无风屏的情况有很大的减小,但风屏带来的温升效应会直接影响到空气折射率的变化.图13为风屏作用下不同β时光程差随γ的变化,与图9对比可得到,受到风屏温升效应的影响虽然Pv的变化趋势一致,但不同β时的Pv值均有显著的增大.可同时考虑到镜面受到的风载压力也会变小,从而由镜面的面形变化导致的成像变化也会减小[17],这需要今后进一步的计算和实验.

图13 加装风屏后,β=0°,30°,60°,90°时Pv随γ的变化Fig.13 After installing the wind screen,change of Pv with γ at β=0°,30°,60°,90°

4 结论

本文借助CFD和有限元方法,分析了2.5 m望远镜及膜圆顶和塔架结构,在给定风速和环境温度的条件下,得到了在不同的风向角-方位轴转动角-镜筒转动角度时望远镜周围空气流速、湍流强度等的变化情况以及对光程差的影响;同时还分析了风屏对望远镜周围的空气流速、湍流强度及温度的影响.对后续天文望远镜塔架结构设计,膜圆顶的结构优化以及风屏结构的应用提供了参考.