基于CEI测量的GEO目标快速轨道恢复

黄俊迦 杜兰 刘泽军 张中凯 周佩元 刘隆迪

(信息工程大学地理空间信息学院 郑州 450001)

1 引言

地球静止轨道(Geostationary Earth Orbit,GEO)因其轨道资源的独特性与稀缺性,成为各国相互争夺的重要太空资源[1-4].由于摄动力等因素的影响,GEO目标需要频繁地实施机动以保持在分配的定点区间内.这种位保机动破坏了常规定轨精度的连续一致性,因此机动后的快速轨道恢复对GEO目标的常规管理至关重要[5].

针对非合作GEO目标的监视预警,还要应对各种随机的特殊任务机动,因此监测系统的快速响应能力也极为迫切.连线干涉测量(Connected Element Interferometry,CEI)是一种基于卫星下行射电信号的被动测量方式,可以全天候跟踪非合作GEO目标且具有隐蔽性,已被应用于GEO卫星的日常机动监视和轨道确定[6].

但是,GEO目标机动后的快速轨道恢复属于短弧定轨.由于GEO目标的静地特性,地基跟踪的轨道力学约束弱,短弧定轨通常有较强奇异性,从而难以保证精度.文献[7]依据测角定轨原理,分析了测轨弧长和测站数对非合作GEO卫星定轨预报精度的影响.小于4 h弧段的单站定轨,位置误差均大于3 km;双站8 h弧长定轨,精度可优于3 km.但该方法数据累积时间长,对测站构型要求较高.文献[8]提出基于9参数星历拟合的短弧运动学定轨方法,针对参数拟合的奇异问题提出了解决措施.利用C频段测距对北斗GEO卫星的实验表明,10 min短弧定轨和5 min预报的位置精度均优于20 m,但该方法仅适用于合作目标.

针对GEO非合作目标的CEI短弧定轨的奇异性,提出一种自适应优化半长轴和附加先验轨道约束的短弧定轨算法.CEI观测量对卫星径向信息不敏感,表现为形亏,而半长轴与平经度有较强误差相关性,表现为数亏.因此,通过附加先验方差约束以减弱算法的病态性,并针对轨道半长轴的初值对定轨结果影响大的现象,提出了半长轴初值的自适应优化方法.利用郑州的CEI测轨系统对亚太七号卫星的实验,验证了该算法对短弧定轨和预报的精度提升,为GEO机动后的快速轨道恢复提供了改进依据.

2 CEI短弧定轨原理

2.1 测轨方程

CEI系统的测量原理如图1所示,CEI观测量是基线两端天线接收到的下行信号经互相关后得到的不足一个波长的相位差[9-11].图中基线AB上的量测方程为:

图1 CEI系统测量原理示意图Fig.1 Schematic diagram of CEI system measurement principle

式中,φ表示相位差观测值(以长度为单位),λ和N为信号的波长和整周模糊度;ρA与ρB表示卫星至主站A与副站B的距离.r(t0)表示卫星信号发出时刻t0卫星位置向量,RA和RB则分别是主副站在接收时刻t1和t2的位置向量.Δtclock表示站间钟同步偏差;Δρatm和Δρins为大气传播延迟和设备延迟的站间差;ε为观测噪声.

连线式CEI通常为数十米至数十千米的短基线,相对于高轨静地GEO卫星,相位差观测量可看作是一种高精度的测角观测量[12-14].为了使GEO卫星的天球面指向精准,至少需要两条相交基线,最为理想的是两条正交基线.

需要指出的是,使用CEI相位差观测的前提是已知整周模糊度N.由于常规机动对GEO轨位的改变通常在千米级,且基线越短对这种变轨越不敏感,因此短基线条件下,可以采用机动前的模糊度解算值.

2.2 短弧定轨方法

GEO卫星的初轨状态量,在地心惯性系(Earth Center Inertial Coordinates System,ECI)下通常采用专用于小偏心率和小倾角的第二类无奇点根数表示,即σ0=(a,e,i,λ0)T.它与经典开普勒轨道根数的关系如下[15-18]:

式中,e为二维偏心率向量;i是二维倾角向量;˜ω=Ω+ω;λ0称为初始时刻的平经度,从春分点计量至该时刻的卫星位置;M0为初始时刻的平近点角.开普勒轨道根数(a,e,i,Ω,ω,M)分别表示轨道半长轴、偏心率、轨道倾角、升交点赤经、近点角距和平近点角.

短弧定轨的力模型可仅考虑二体问题,弧段内任意时刻tj的线性化观测误差方程可表示为:

其中δσ0是初轨状态的改正数向量,Δφj是观测值与理论计算值的差值(即O-C),vj称为观测残差,系数矩阵为

式中的复合偏导数不再赘述.

采用最小二乘平差,即满足VTP V=min,则可求解初轨状态量的最佳改正数向量:

其中,V是观测残差组成的列向量,P是观测权矩阵,l是自由项,即弧段内Δφj组成的列向量;由于GEO对地的构型基本不变,权矩阵P可取单位阵.

3 短弧定轨的改进算法

由于精度要求不高,短弧定轨也可以直接在地心地固系(Earth Centered Earth Fixed System,ECEF)下实现.二体问题下的ECEF初轨状态,仅需要将第二类无奇点根数的历元平经度λ0改换为历元时刻的定点经度λe0,即

式中S0是t0时刻的格林尼治时角.

若忽略小倾角和小偏心率的影响,任意时刻t的定点经度λe能够反映GEO卫星的对地变化,即

式中n和ne分别是卫星运动和地球自转的平均角速率,由于GEO的静地特性,二者仅有微小偏差.

此外,依据GEO工作卫星的轨位分配机制,定点经度λe通常规定在标称经度附近的±0.1°内变化,这也为该参数的先验约束带来了便利[19].

3.1 病态性分析

基于CEI的GEO短弧定轨有较强的病态性,表现为相互关联的形亏和数亏.

(1)因CEI测角本质导致的形亏

CEI的短基线使得高轨卫星下行信号的球面波传播可理想化为平面波传播.此时,CEI相位差表现为卫星相对于基线的方向变化信息,CEI干涉测角示意图如图2所示.因此,这种“测角”类型观测量对卫星的径向位置不敏感,且GEO静地特性决定了其较弱的轨道力学约束,短弧情况下约束性更加弱化[20].在缺乏卫星测距观测量的情况下,仅基于CEI的GEO短弧定轨模型鲁棒性差,导致无法解算半长轴a.

图2 CEI干涉测角示意图Fig.2 Angular measurement of CEI

(2)因轨道状态参数相关性引起的数亏

由开普勒第三定律n2a3=µ(µ是地球引力常数),定点经度λe与半长轴a的改正数之间存在线性漂移,即

式中,Δλe为定点经度的变化量,Δn为卫星运动平均角速率和地球自转平均角速率的差值,Δa为半长轴的变化量.

前面分析了CEI的形亏使得短弧定轨无法改进半长轴a,这里半长轴的初值偏差又将直接引起定点经度的线性漂移.因此,历元时刻定点经度λe0的解算精度与半长轴初值的精度具有密切关系,若处理不好两者均难以得到改进.

3.2 改进算法

为了削弱短弧定轨的病态性,必须引进先验轨道约束.除了增加常规的参数先验协方差约束,还必须确定最优的半长轴初值.

(1)附加先验约束

依据GEO的机动特性和定点控制区规定,部分初轨参数的先验均方差约束为: 半长轴a取±20 km,历元时刻的定点经度λe0和倾角分量iy取±0.1°.

附加先验约束的初轨改正法方程为:

显然,先验约束的实质就是增强法矩阵的正定性,从而改善矩阵求逆的病态问题.

(2)自适应优化半长轴初值

常规定轨对初值精度要求不高.以GEO卫星为例,半长轴的初值可取为静止轨道的标称值(42165.76 km),定点经度的初值λe0可取为定点经度的标称值,其他轨道参数均取0即可.

但是,在实际解算中发现,若半长轴初值在标称值附近一定范围内随机取值,解算精度会出现较大差异.在没有其他辅助测量手段的前提下,本文经验性地设计了一种自适应选取半长轴初值的优化算法.其流程如下: 截取静止轨道标称值的±20 km作为探测窗口,以0.2 km为步长遍历窗口并为半长轴赋初值,分别解算轨道.考察解算得到的偏心率序列(即将偏心率极小值对应的半长轴作为半长轴的最佳初值.偏心率极小值也能够一定程度上反映出GEO的近圆特性.

经大量仿真和实测数据验证,与采用固定静止轨道半长轴标称值相比,该优化算法的定轨精度更高,且更加稳健.

4 实验

利用位于郑州的L型正交双基线CEI测轨系统,对亚太七号(Asia-Pacific STAR 7,APSTAR 7)进行短弧定轨和预报实验.CEI的东西和南北基线分别为75 m和35 m,亚太七号下行Ku信标信号的频点为12.442 GHz.由于GEO机动后的数小时通常不提供精密轨道,为了验证算法分别采用了CEI的仿真数据和实测数据.

4.1 仿真实验

轨道仿真: 包含东西机动段在内的1 d数据.初始时刻为UTC (Coordinated Universal Time)2022-06-01 02:00:00,机动时段为当天的07:10:06-07:30:06,共20 min.机动采用持续小推力,在近地点附近实施.仿真采用卫星工具包(Satellite Tool Kit,STK)的Astrogator模块,顾及了10×10阶地球引力位、日月引力摄动和光压.关键时刻的轨道根数见表1.

表1 APSTAR 7卫星的开普勒轨道根数Table 1 Keplerian orbital elements of APSTAR 7

图3是轨道半长轴和轨道倾角的时序.可以看出,非机动期间,半长轴有显著的半天周期震荡,机动期间轨道半长轴快速下降了4 km,轨道倾角则几乎无变化.

图3 东西机动的轨道半长轴和轨道倾角时序Fig.3 Semi-major axis and inclination series including the east-west maneuver

CEI数据仿真: 依据CEI的相位测量方程和7.5 mm随机噪声水平,仿真生成1 d的卫星跟踪数据,采样率为10 Hz.假定初始模糊度已知,且暂不考虑模糊度失锁或周跳现象.

机动后轨道恢复及其精度评定: 利用机动结束后30 min内的CEI数据解算弧段中间时刻的初轨改正,并外推10 min.仿真轨道作为真值用于评估短弧定轨-预报段的轨位精度.需要说明的是,为了保证蒙特卡洛仿真的算法稳定性,仿真了20次CEI数据,统计轨道解算精度.

在无轨道先验约束条件下,CEI短弧定轨不收敛.依据(10)式增加了部分参数的协方差约束条件后短弧定轨均收敛.

令半长轴的初值在静止轨道的半长轴标称值附近-20 km-20 km窗口内变化,短弧定轨的误差均方根值(Root Mean Square,RMS)随之变动,如图4所示.图中R、T和N分别是初轨位置误差的径向、切向和外法向分量.显然,短弧定轨的精度对半长轴的初值采用值异常敏感,尤其是R位置分量,这与CEI的测角性质一致.此外,可以看到初值取标称值时并非对应于短弧定轨误差最小的情况.

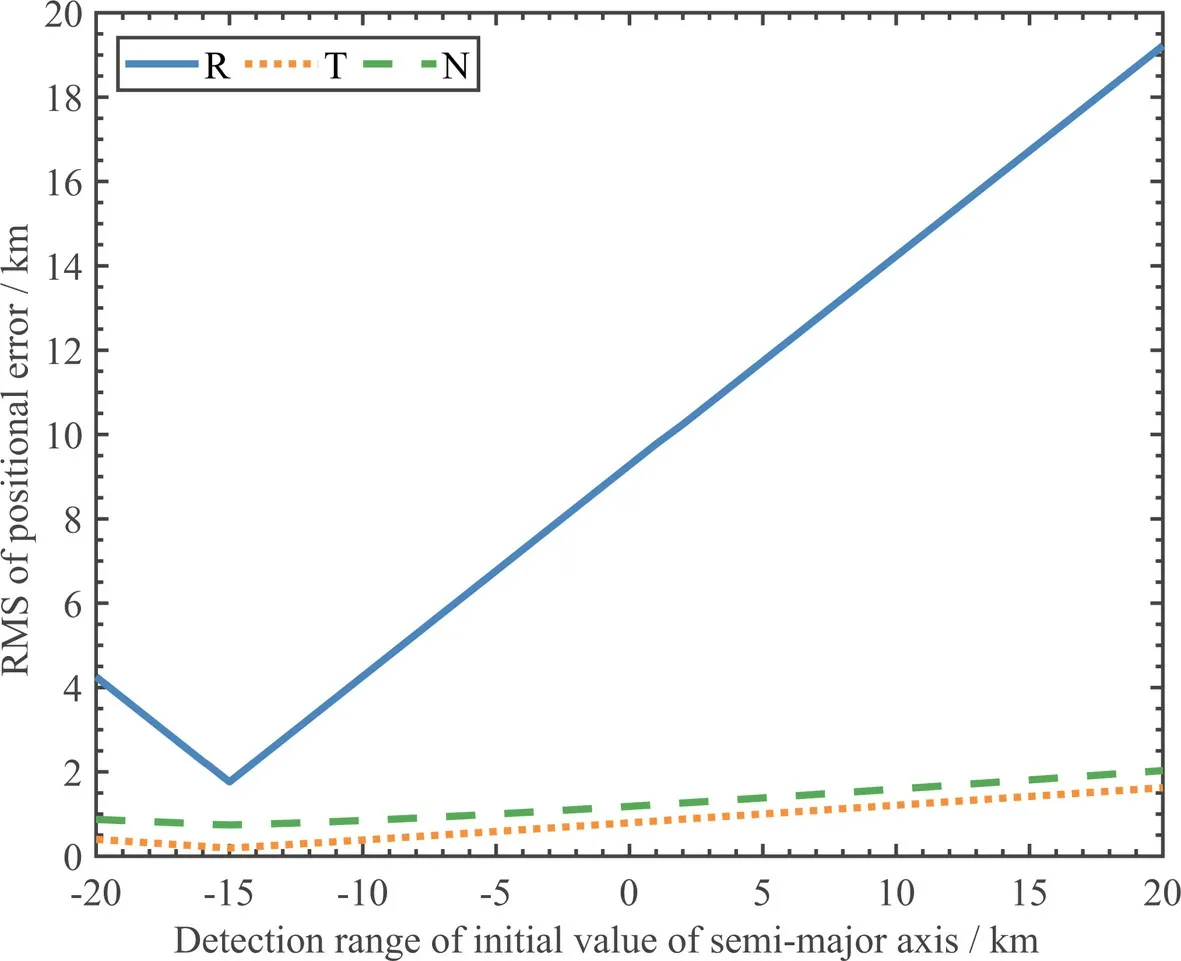
图4 短弧定轨的位置误差RMSFig.4 RMS of the positional errors of the short-arc orbit determination

为此,采用自适应优化求解半长轴初值的经验算法.图5给出了初值在半长轴标称值附近±20 km范围内求解的偏心率时序.令偏心率取极小值时对应最佳的半长轴初值,可见该值比标称值低约15 km.

图5 半长轴初值与短弧定轨解算的偏心率时序Fig.5 Initial values of semi-major axis and the solved eccentricities of the short-arc orbit determination

分别采用半长轴的标称值和优化值作为初值进行短弧定轨和预报.表2为20次仿真解算的轨位误差RMS统计,图6为其中一次解算的轨位误差时序,图中实线和虚线分别对应30 min的短弧定轨段和10 min的预报段.可以看出: (1)由于CEI的测角本质,R分量的轨道恢复精度始终低于T和N分量,采用固定静止轨道半长轴标称值时(图a),R分量误差接近10 km;(2)采用自适应优化的半长轴初值后,R分量改善最为显著,R、T、N位置分量误差的RMS均优于3 km;(3)优化后的半长轴初值,20次的计算平均值比标称值小14.76 km,且该数值的波动性不大(见表2).

表2 仿真数据的短弧定轨和预报误差RMS统计Table 2 Error RMS statistics of the short-arc orbit determination and orbit prediction with simulation data

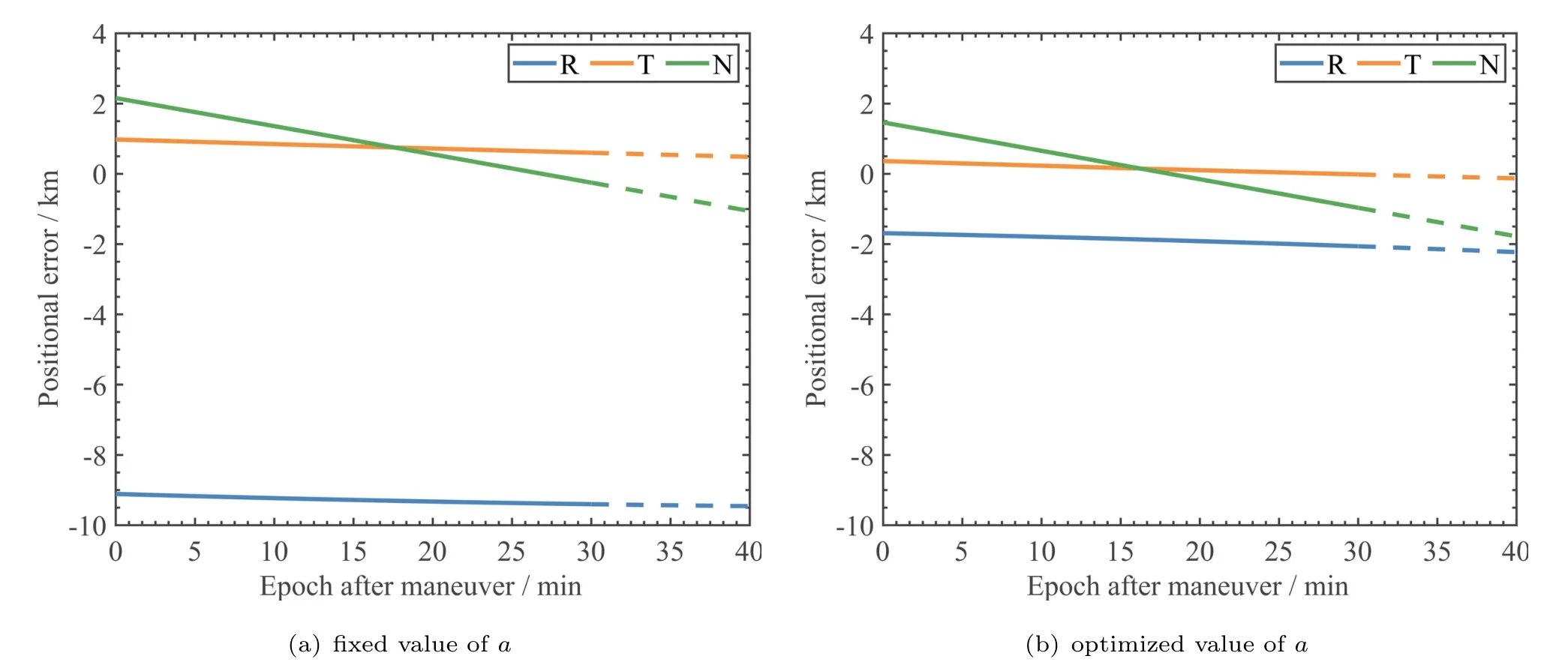
图6 仿真数据的两种半长轴初值对应的短弧定轨和预报精度Fig.6 The short-arc orbit determination and orbit prediction accuracy with two adopted semi-major axes for simulation data

4.2 实测数据实验

目前机动力的高精度建模尚有困难,机动后通常需要重新累积测轨数据,因此机动后的数小时内无法实现长弧定轨[21-22].为了模拟机动后的快速轨道恢复场景,在亚太七号的非机动期间(2019年1月7日至10日)分别截取了4段CEI数据进行短弧定轨,并利用国家授时中心提供的基于测距的长弧定轨结果(米级精度)进行外符合精度评估.CEI测量系统的配置和亚太七号的定点经度等与仿真实验一致.

采用相同的先验信息约束进行30 min短弧定轨和10 min预报,考察了两种半长轴初值方案:

方案A-采用静止轨道的半长轴标称值;

方案B-采用自适应优化的半长轴.

图7和表3给出了4次实验的短弧定轨-预报精度,图中pos表示位置误差.对比A、B两个方案,可以看出: (1)自适应优化得到的半长轴初值较为稳定,比方案A的固定标称值小7.5-10 km;(2)优化后的半长轴初值对轨道恢复精度改善显著,尤其是R分量,不仅是短弧定轨段,还极大改进了预报精度,三维位置整体预报精度从A方案的5 km减小到3.5 km左右,前3段甚至优于1.5 km.

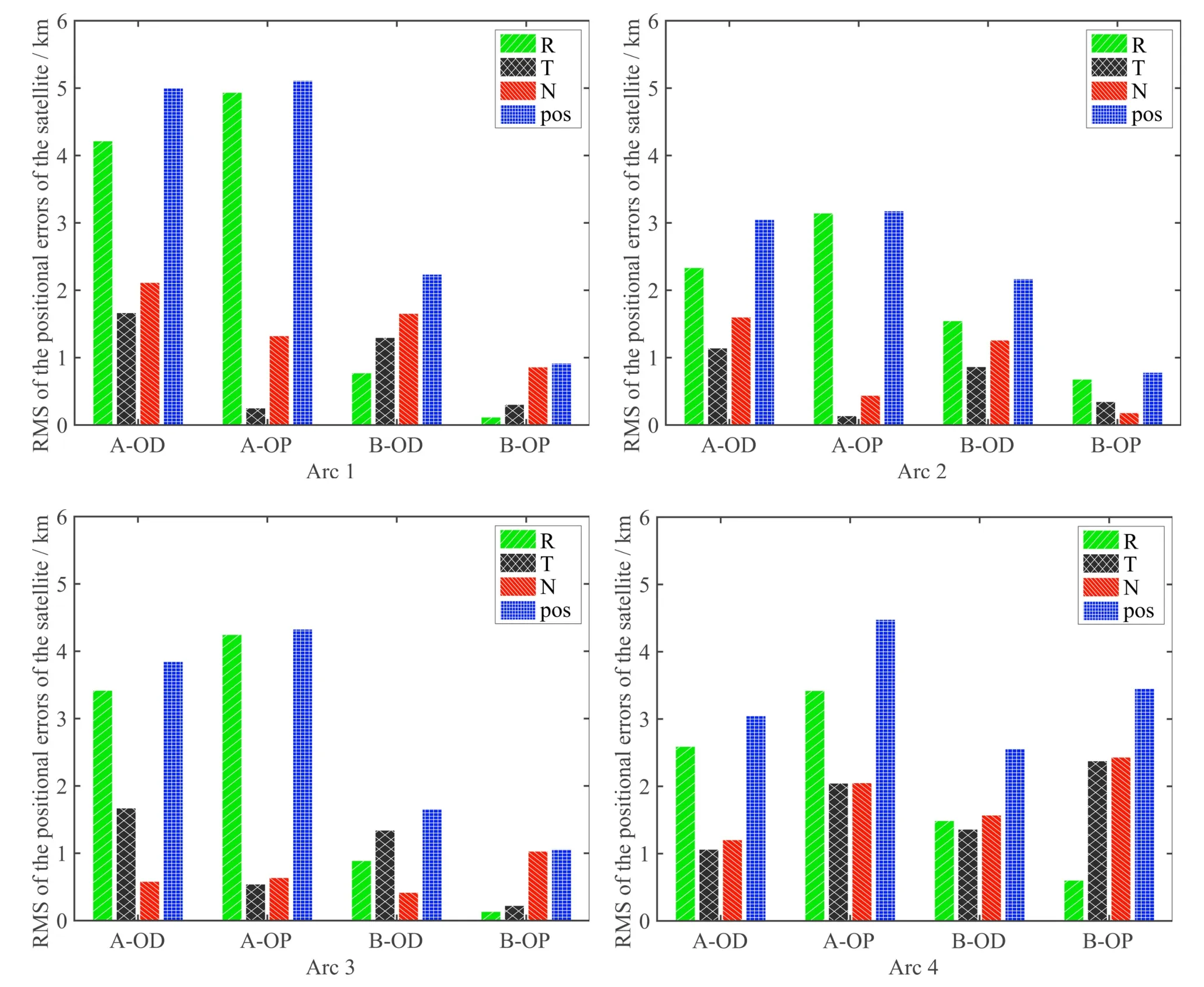
图7 实测数据的短弧定轨和预报精度比较(A: 采用静止轨道的半长轴标称值,B: 采用自适应优化的半长轴)Fig.7 Comparisons of the short-arc orbit determination and orbit prediction accuracy with real data (A: With nominal value,B: With optimized value)

因此,对于非合作GEO目标公里级的轨道恢复精度来说,采用自适应优化的半长轴初值的B方案优于采用静止轨道半长轴标称值的A方案,能够用于机动后的快速轨道恢复.

5 结论

短基线相位干涉测量CEI是一种基于射电波段的高精度被动测角技术,非常适合跟踪非合作GEO目标.但是,纯测角的GEO短弧定轨算法因病态性无法解算轨道半长轴,导致定轨精度不高甚至定轨失败.

本文提出了一种自适应先验轨道约束的CEI短弧定轨改进算法.综合利用了优化半长轴初值和先验方差约束的策略,削弱了轨道解算的病态性并提高了定轨精度.基于75 m×35 m的正交双基线CEI仿真和实测数据实验表明,30 min短弧定轨和10 min预报的轨位精度优于4 km.改进算法为机动后GEO非合作目标提供了可行的快速轨道恢复方案.

致谢感谢国家授时中心提供了亚太七号卫星的轨道数据.