球状星团成员星的空间相关性分析*

林伟斌 陈 楠 林偲蔚

(1 福州大学空间数据挖掘与信息共享教育部重点实验室福州 350108)

(2 福州大学数字中国研究院(福建)福州 350108)

(3 南京大学地理与海洋科学学院南京 210023)

作为银河系中已知年龄最大的天体之一,球状星团相比疏散星团包含了更多的恒星,一般由105-107颗恒星聚集而成[1-2].其内部的恒星均受到星团中心引力的牵引,仿佛卫星一样共同围绕着星团中心运动,同时高度地向中心集中,在球状星团内部形成了紧密有序的球状结构[3].球状星团成员星的空间分布特征和机理是探索宇宙和星系的形成与演化、恒星的形成与演化、恒星动力学特征、银河系结构和动力学等许多研究中的重要内容[4-6].通过研究球状星团的空间分布特征和机理有助于揭示恒星演化的线索和获取银河系演化的历史信息,从而进一步探究星系形成与演化的规律[7-10].

随着现代观测技术的革新与发展,球状星团观测基础资料和信息源不断增加.目前对球状星团内部空间结构和内在机理的研究方法和理论已日益丰富,学者们引入了一系列如两点相关函数、最近邻分析、渗流、功率谱分析、BA(Binning Analysis)和KS (Kolmogorov-Smirnov)检验、团分析和多重性函数等[11-21]分析方法对球状星团中成员星的空间分布结构和特征展开了系列研究,并取得了丰富的成果.

球状星团内部的成员星如同一个个点状要素构成了球状星团独特的空间结构.在地学领域中,针对地学点状要素,学者们已经建立了完善的空间自相关性统计检验指标,提出了特有的空间自相关性的计算方法,并构建了成熟的空间自相关分析理论.陈彦光[22]对基于莫兰(Moran)统计量的空间自相关过程的数学表示进行规范化整理,给出了Moran指数的理论解释,总结并发展了Moran指数的3种计算方法,并对鹤壁市乡镇总人口进行了空间自相关分析.考虑到球状星团中成员星与地学中点状要素的相似性,能否从地学研究的范式探究球状星团成员星空间分布的特征,成为前人研究所衍生出的全新问题.目前,球状星团中成员星的确定方法已臻成熟[23],许多球状星团中也有足够数量的成员星,这为深入揭示成员星的空间分布特征奠定了良好的理论基础和数据基础.

作为地理学的核心研究方向之一,空间自相关被广泛应用于定量分析地理现象或空间实体属性值之间的关联程度[24].空间自相关是指某些变量在同一或不同分布区域内的观测数据之间潜在的相互依赖性[25],常用于分析要素的空间集聚和变化规律[26].学者利用空间自相关原理分析各种地理现象,研究了不同区域内地理要素的集聚与分散程度.如丁洋等[27]采用空间自相关分析对松花湖湖区富营养化水平的空间相关性与聚集度状况进行了研究;杨振奇等[28]对裸露砒砂岩区小流域土壤侵蚀空间自相关特征及影响因素进行了分析.不局限于地学领域,空间自相关理论亦已被用于生态学[29]、生物学[30]、经济学[31]、流行病学[32]和犯罪学[33]等诸多领域,在研究事物的规律性现象、空间分布格局、时空变化规律、空间异质性分析等[27]方面取得了大量的研究成果.基于此,空间自相关已成为检验具有空间位置的某要素的观测值是否显著地与其相邻空间点上的观测值相关联的有效方法[34-35],且已与众多学科进行了交互,但是该理论尚未被应用于天文学展开相应的研究工作,使得我们缺乏以下关于星团的知识--星团的空间分布格局如空间异质性、空间自相关性、空间各向异性等,而这些知识对于搜寻团星、星团演化等研究具有不可替代的作用.

基于此,本研究选择NGC (New General Catalogue) 104、NGC 5139、NGC 6121共3个球状星团作为研究样区,以Gaia EDR3 (Gaia Early Data Release 3)为基础数据源,将地学的空间自相关理论应用于天文学.通过计算全局Moran指数得到球状星团成员星各恒星参数的空间分布特征,根据Moran散点图与LISA (Local Indicators of Spatial Association,空间关联的局部指标)集聚图得到各恒星参数的局部空间分布特征.空间自相关的理论方法为研究球状星团成员星空间分布特征提供了思路和理论.该研究能够系统地定量化描述球状星团成员星空间分布特征,为进一步揭示球状星团成员星空间分布特征的机理提供了地学辅助手段和全新的切入点,深化了对球状星团成员星的认识,开辟了用地学方法研究球状星团空间分布特征的新方向.

2 研究区概况与数据来源

2.1 研究区概况

NGC 104、NGC 5139、NGC 6121这3个球状星团都拥有丰富的成员星,它们被广泛用于开展球状星团结构与演化的研究.这3个球状星团的具体介绍如表1所示.

表1 球状星团信息[36-38]Table 1 Properties of the globular clusters[36-38]

2.2 数据来源

星表是表示恒星在某一历元的位置、运动、亮度等信息的集合[39].盖亚星表是研究球状星团十分重要的资料,它是由欧洲航空局“盖亚”空间天文台发布的.于2020年12月公布的Gaia EDR3含有超过18亿颗恒星的高精度数据,被广泛用于球状星团结构与演化的研究.以恒星参数的科学性为基础,本研究从盖亚星表中选取了视差parallax、总自行pm、赤经自行分量pmra、赤纬自行分量pmdec、G波段平均亮度gm、BP波段平均亮度bp、RP波段平均亮度rp、色指数bp-rp、色指数bp-gm、色指数gm-rp共10个恒星参数,如表2所示.

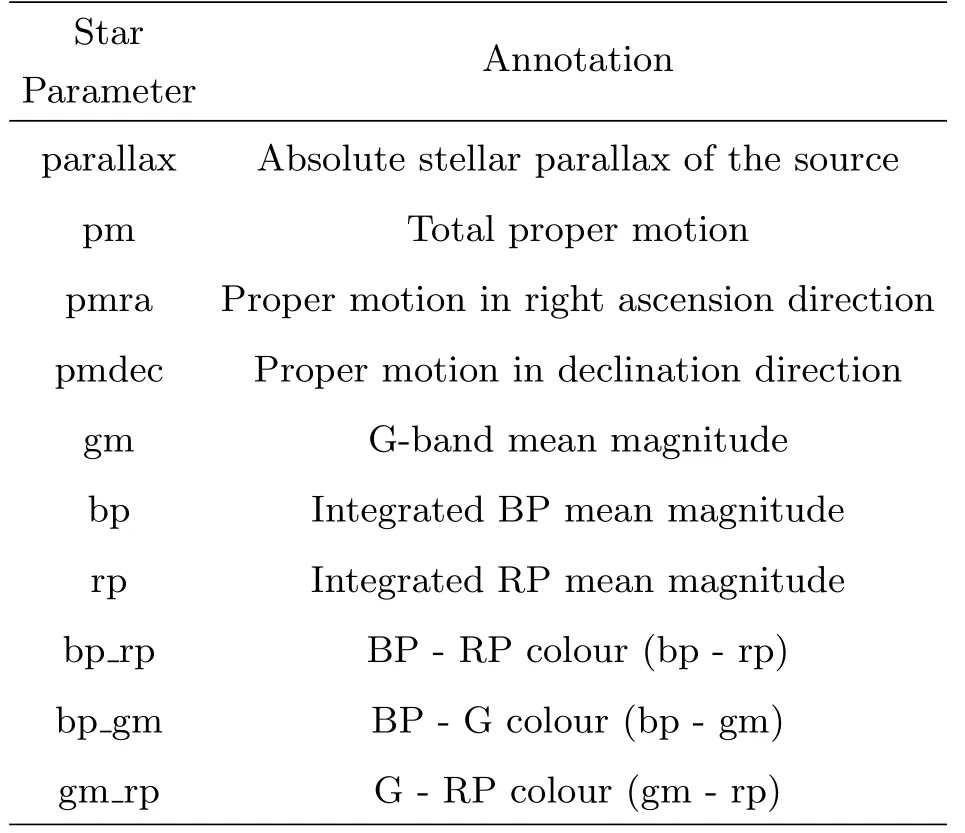
表2 恒星参数Table 2 Parameters of star

3 研究方法

3.1 数据预处理

3.1.1 成员星的选取

研究球状星团,首要工作就是准确判定球状星团的成员星,常见的方法是通过球状星团成员星和场星在物理性质上的差异来进行判定.球状星团的所有成员星作为一个整体在一些恒星参数上会区别于场星,如亮度、自行、视向速度等.Vasiliev等[40]根据Gaia EDR3数据,采用混合建模的方法,综合亮度和运动属性,完成了球状星团成员星的判定,给出了每颗恒星是成员星的概率.因此,本研究采用Gaia EDR3星表中Vasiliev等[40]给出的成员概率,选取成员概率大于0.9的恒星作为各球状星团的成员星,其中NGC 104的成员星数量为7249颗,NGC 5139的成员星数量为6431颗,NGC 6121的成员星数量为1784颗.3个球状星团成员星的空间分布如图1所示,其中坐标系是由银道坐标系转换成直角坐标系得到,坐标系原点为太阳,X轴指向银心方向,Y轴的方向是银道面中经过原点并与X轴垂直的方向,Z轴指向北银极.

图1 球状星团成员星的空间分布Fig.1 The spatial distribution of the member stars of the globular clusters

3.1.2 恒星距离的计算

距离是进行空间相关性分析的基础.要想计算出恒星之间的距离,首先要获取恒星的位置信息.Bailer-Jones等[41]根据Gaia EDR3数据,采用概率方法估算出14.7亿颗恒星到太阳的距离.结合Gaia EDR3星表提供的成员星在银道坐标系下的银经和银纬信息,可得到成员星的坐标数据.成员星之间的距离可以根据坐标计算得到.

3.1.3 空间权重的确定

进行空间自相关分析,空间权重是必不可少的.Anselin[42]提出了确定空间权重的方法,把空间位置的相邻关系分为3类: 邻接关系、距离关系和最近k点关系.本文采用距离关系中的距离幂衰减形式构造空间权重矩阵,具体构造形式为

其中,Wij是空间权重矩阵第i行第j列的元素,dij是成员星j到成员星i的欧式距离(单位为pc),α一般取-2[43].

3.2 空间自相关

空间自相关分析可以研究球状星团聚集特征.聚集特征包含正相关和负相关,若球状星团成员星的恒星参数值变化趋势与其邻近的成员星相同,则为正相关;反之则为负相关.空间自相关中,全局空间自相关用于判断要素值在空间上是否存在聚集性[44],可用全局Moran指数来衡量;局部空间自相关用于判断聚集类型从而反映哪些区域发生了聚集[42],可用局部Moran指数来衡量.

3.2.1 全局空间自相关

全局Moran指数可以衡量全局空间自相关性,反映成员星恒星参数值聚合或离散的程度,计算公式为

其中,I表示全局Moran指数,n为成员星数量,xi和xj分别是成员星i和j的参数值,为参数均值.I的值介于-1到1之间.当I＞0,表示成员星的参数值在空间上呈正相关分布,其值越大,空间相关性越明显,即存在高值与高值聚集或者低值与低值聚集的现象;当I＜0,表示成员星的参数值在空间上呈负相关分布,其值越小,空间差异越大,即存在低值与高值聚集的现象;当I=0,表示成员星的参数值在空间上呈随机分布[44].

在空间自相关分析中,可通过Z检验对全局Moran指数进行统计学检验,检验标准为0.05.通过Z检验可获得Z值及P值,Z值计算公式为

其中,E(I)为I的期望值;Var(I)为I的方差.当I＜0且Z(I)＜-1.96时,成员星参数值间存在显著的负相关关系;当I＞0且Z(I)＞1.96时,成员星参数值间存在显著的空间正相关性;当I=0或-1.96 ≤Z(I) ≤1.96则表示不存在空间相关性,呈完全的空间随机分布模式[45].

3.2.2 局部空间自相关

局部空间自相关指数可以反映某一空间单元的属性值同其邻接空间单元上同一属性值的相关程度[46].局部Moran指数的计算公式为

其中,Ii表示局部Moran指数.

与全局Moran指数一样,局部Moran指数也需要结合Z值对其取值进行说明,计算公式为

其中,E(Ii)为Ii的期望值;Var(Ii)为Ii的方差.Ii与Z(Ii)取值意义与全局Moran指数相同.

4 结果与分析

4.1 全局空间自相关研究的结果

为探讨球状星团中成员星的不同恒星参数的空间关联程度,通过(1)式对球状星团NGC 104、NGC 5139、NGC 6121的成员星分别计算其全局Moran指数,结果如表3所示.

从3个球状星团的10个恒星参数的全局Moran指数I可以得到其值均大于0,且Z得分均通过了95%置信度的检验,P值均小于0.005且基本都为0,说明3个球状星团各恒星参数表现出正相关性.其中,视差是从两个不同位置观察恒星所得到的方向之差,当成员星之间的距离越近时,其观测到的方向差也就越小,因此视差表现为正相关性.成员星的自行(pm、pmra、pmdec)均表现为正相关性,这与球状星团成员星的自行属性具有一定的规律性相符合[47-48].通过表3可得,色指数bp-gm与gm-rp相对于其他恒星参数来说,其全局Moran指数总体来说较大,表现出明显的正相关性.色指数为不同波段的星等差,其大小能反映恒星的表面温度[49],且与恒星的颜色密切相关.由此可以推断出:当球状星团成员星之间的距离越近,它们色指数bp-gm与gm-rp的值越接近,其表面温度就越相近,此时它们之间的颜色也越相似.

4.2 局部空间自相关研究的结果

对3个球状星团的数据分别进行处理得到Moran散点图,如图2所示(以色指数gm-rp为例).

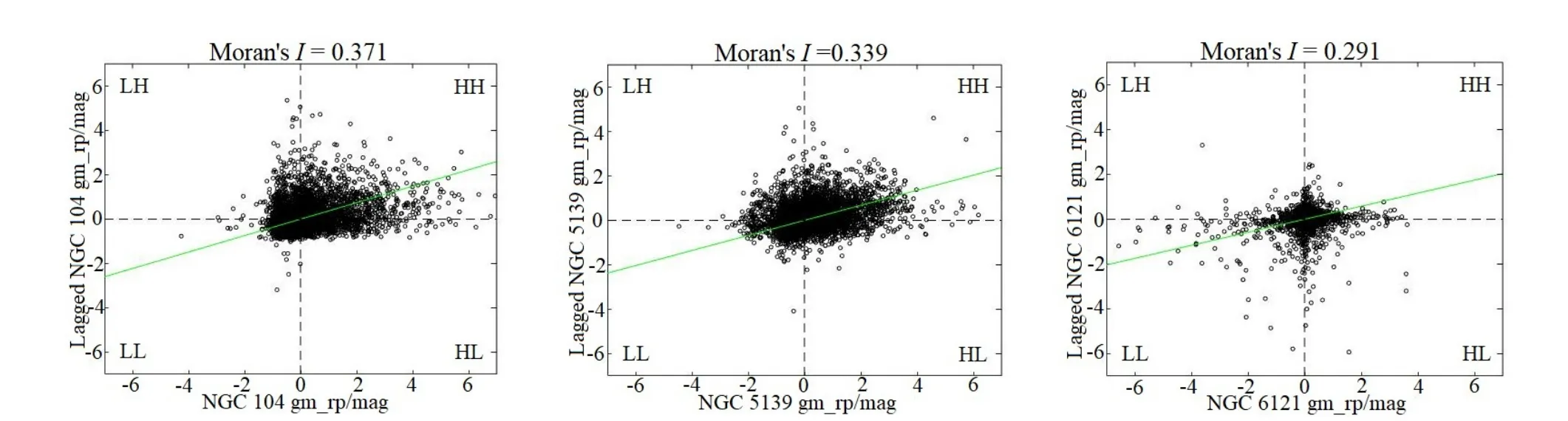
图2 色指数gm-rp的Moran散点图Fig.2 Moran scatter plot of the colour index gmrp

图2中横坐标表示色指数gm-rp的标准化值,纵坐标表示色指数gm-rp的空间滞后值.散点图第1象限High-High (HH)表示该成员星的色指数gm-rp与周围成员星的色指数gm-rp都较高,成员星的色指数越大,其表面温度也就越低,它的颜色越偏向橙红色;第2象限Low-High (LH)表示该成员星的色指数gm-rp较低,周围成员星的色指数gm-rp较高;第3象限Low-Low (LL)表示该成员星的色指数gm-rp与周围成员星的色指数gm-rp都较低,成员星的色指数越小,其表面温度也就越高,它的颜色越偏向蓝紫色;第4象限High-Low (HL)表示该成员星的色指数gm-rp较高,周围成员星的色指数gm-rp较低.其中,成员星位于HH与LL象限说明其参数具有强烈的正相关性,而成员星位于LH与HL象限说明其参数具有强烈的负相关性.

Moran散点图中球状星团成员星占各象限的比例如图3所示.通过图3可以看出,球状星团NGC 104与NGC 5139在10个恒星参数Moran散点图中各象限占比的差距不大,而NGC 6121与这2个球状星团之间的差距存在明显的波动,可能是因为NGC 104与NGC 5139成员星的数量较多,而NGC 6121成员星的数量较少.当球状星团成员星的数量足够多时,其各恒星参数的Moran散点图各象限的占比可能会趋于稳定.总的来看,3个球状星团的成员星落在HH与LL所占的比例均大于落在LH与HL所占的比例,且呈现出HH与LL的成员星所占的比例越高,其全局Moran指数越大,空间正相关性趋势越突出.

图3 Moran散点图成员星占比Fig.3 Proportion of member stars in each quadrant in Moran scatter plot

对球状星团局部成员星恒星参数的相关程度的定量分析可以通过LISA集聚图得到.其包含了4种空间关联特征(High-High、Low-High、Low-Low、High-Low)以及非显著性(Not Significant,NS).构建95%置信度的LISA集聚图,如图4所示(以色指数gm-rp为例),各空间关联类型所占比例如图5所示.

图4 色指数gm-rp的LISA集聚图Fig.4 LISA agglomeration map of the colour index gm-rp

从图5可以看出,High-High类型占比较大的恒星参数为bp-gm,Low-Low类型占比较大的恒星参数为gm-rp,Low-High与High-Low类型在各恒星参数中占比较少,而非显著性类型在各球状星团的恒星参数中均有占比,这与全局Moran指数计算结果相吻合.总的来看,LISA聚集图总体表现出正相关性的趋势,与全局Moran指数和Moran散点图的全局空间分布特征相符.

4.3 贡献与局限性

本研究基于地学的空间自相关理论对球状星团的空间相关性进行研究,区别于研究球状星团的成团性、空间分布情况的方法,从空间分析的视角重新探索球状星团成员星的空间分布特征,把空间分析方法引入球状星团的研究中,为空间自相关理论拓宽了其应用范畴,也为研究球状星团提供了新思路.在后续工作中,尝试将地统计学方法引入球状星团的研究中,试图揭示球状星团成员星的空间分布规律.

区别于以往的天文学理论研究,本文采用了基于地学的空间分析方法对球状星团的空间分布特征和空间集聚特性进行了分析,与前人研究的区别总结如下:

(1)本研究是对球状星团成员星的恒星参数的空间分布特征进行研究,而现代数理统计方法更多的是对成团性等成员星空间分布情况进行描述;

(2)将地学的空间自相关理论引入球状星团的研究,分析其成员星全局和局部的空间自相关特征.

然而,本研究仍存在以下局限性:

(1)本研究基于Gaia EDR3数据选取多个恒星参数,这几个参数均属于使用较为常规、广泛的参数.下一步研究,可以更加充分挖掘其他参数信息(尤其是恒星质量、年龄),进一步研究成员星的演化程度之间的关系,有利于对球状星团的深入研究;

(2)本研究证实将地学的空间自相关理论引入球状星团的研究,分析其成员星的空间自相关特征具有可行性.然而,天文观测数据是不断更新的,随着Gaia后续数据的释放,其观测数量及精度全面提升,未来我们可以使用最新发布的Gaia数据进行研究.

研究的应用价值在于: 空间自相关理论有望广泛应用于球状星团空间特征的研究,其研究成果可用于球状星团成员星的搜寻.

5 结论

本研究利用Gaia EDR3观测资料,对球状星团NGC 104、NGC 5139、NGC 6121进行了空间自相关分析,讨论了其成员星恒星参数的空间分布特征.其中,本研究引用了Vasiliev等[40]的成果,以成员概率不小于0.9为3个球状星团成员星判据.此外,本研究通过计算全局Moran指数获得球状星团成员星各恒星参数的全局空间相关性,根据Moran散点图与LISA集聚图分析其局部分布特征.通过上述研究,得出以下结论:

(1)本文初次尝试了将空间自相关理论应用到球状星团的研究中,实现了对球状星团空间分布特征的描述.实验结果表明,用空间自相关理论进行球状星团的空间自相关特征研究具有可行性;

(2)球状星团NGC 104、NGC 5139、NGC 6121的10个恒星参数均呈现空间正相关性,其中色指数bp-gm与gm-rp的正相关性较为强烈,表明距离越相近的成员星的颜色特性越趋于相同,其表面温度也会越相近;

(3)球状星团NGC 104、NGC 5139、NGC 6121的10个恒星参数总体表现为局部空间聚集特征,且成员星在Moran散点图中HH与LL所占比例越高,其空间正相关性越突出;

(4) LISA聚集图总体表现出空间正相关性,其中High-High类型与Low-Low类型分别在bp-gm与gm-rp中占比较大,这与全局空间自相关结果吻合.