基于Mel-GADF与ConvNeXt-T的变压器铁心松动故障诊断方法

2024-03-26万可力马宏忠崔佳嘉

电力自动化设备 2024年3期

万可力，马宏忠，崔佳嘉，王健

（河海大学能源与电气学院，江苏南京 211100）

0 引言

随着电力行业的快速发展，变压器作为电网主设备在电力传输中得到了广泛应用［1-2］。研究表明，变压器的主要故障为机械故障，其中包括变压器铁心松动故障［3］。一旦发生该类故障，将对电力变压器抵御短路电流冲击能力产生巨大的威胁，容易诱发部分电气故障、发热等［4-5］。因此，对电力变压器铁心松动故障开展监测、诊断等相应研究对变压器安全稳定运行和维持电能质量具有重大意义。

现有的变压器铁心松动故障诊断技术往往采用振动法，将振动加速度传感器放置在变压器油箱表面，通过实时采集变压器在运行时的振动信号来判断变压器处于何种工况，以及是否发生铁心松动故障［6］。文献［7］针对一台三绕组变压器建立了全电容、电感矩阵参数下的振荡波时域数学模型，从变压器自身属性分析了振荡波的机理。文献［8］利用总谐波畸变率作为振动信号的特征指标诊断变压器铁心松动故障，解决了变电站现场基频幅值受环境因素影响的问题。文献［9］通过分析变压器油箱表面的振动信号特征频率完成对变压器铁心松动故障的诊断。然而，振动法比较依赖传感器的安装位置及性能，且在大规模巡检时，测量变压器振动信号耗时长，因此需要采用效率更高的方法进行变压器故障诊断。

近年来，通过分析声纹信号对变压器进行故障诊断的方法凭借其特有的非接触式、测量便捷及传感器成本较低的优势一跃成为目前变压器故障诊断的研究热点之一。文献［10］提出了一种基于Gammatone 滤波器倒谱系数（gammatone filter cepstral coefficient，GFCC）和鲸鱼算法优化随机森林（whale algorithm-random forest，WGRF）的变压器机械故障声音诊断方法，有效提取了变压器声音信号中的机械状态信息并对机械故障进行分类。文献［11］通过噪声源成像定位技术对变压器套管故障进行诊断和定位。文献［12］提出一种基于改进的梅尔频率倒谱系数（Mel frequency cestrum coefficient，MFCC）和三维卷积神经网络（3D-convolutional neural networks，3D-CNN）的变压器声纹识别模型，提取变压器铁心松动故障的声纹特征，完成变压器铁心松动故障程度的分类。文献［13］使用间断伽辽金有限元法对变压器进行近声场瞬态重构，得到变压器近声场的分布规律，同时构建Pearson 均衡相似系数，优化了声纹监测点的位置。文献［14］提出一种改进小波包-反向传播（backpropagation，BP）神经网络算法实现对变压器的放电与机械故障诊断，解决了变压器机械噪声易受干扰的问题。文献［15］提出了基于变压器振动噪声及BP神经网络的故障诊断方法，为变压器运维人员提供了一种带电巡检的有效途径。然而上述方法仍存在故障诊断精度不高、适用范围不广、网络结构复杂、对样本数量需求较高的问题。

利用原始声纹数据生成梅尔（Mel）时频谱图，并结合神经网络的方法在解决变压器故障诊断问题上有不错的效果，但是该方法的识别精度还有提升空间。为解决此问题，本文提出一种基于梅尔-格拉姆角差场（Mel-Gramian angular difference fields，Mel-GADF）与ConvNeXt-T 网络相结合的变压器铁心松动故障诊断方法。利用短时傅里叶变换（short-time Fourier transform，STFT）及Mel 滤波器生成Mel 时频谱图。同时采用格拉姆角场（Gramian angular fields，GAF）变换将原始时序数据生成格拉姆角和场（Gramian angular summation fields，GASF）、格拉姆角差场（angular difference fields，GADF）二维时频谱图，将Mel时频谱图与GASF、GADF 二维时频谱图融合获得Mel-GASF、Mel-GADF 二维特征时频谱图。将所有二维特征频谱图放入ConvNeXt-T 网络训练，找出训练效果最佳的模型从而完成对变压器铁心松动故障的诊断。

1 声纹信号处理

1.1 时频谱图

时频谱图能够较好地反映原始信号的频率、幅值随时间变化的关系，同时也代表了信号在不同时间下的频率能量分布，因此现有技术多将提取声纹信号时频谱图作为变压器故障诊断中提取特征量的关键步骤之一［16］。通过对原始声纹信号进行分帧、加窗及离散傅里叶变换后，按照时间维度将数据堆叠形成二维时频谱图。本文选取变压器正常工况下某0.5 s 的声纹信号作为原始数据（采样频率为50 kHz），首先利用交叠分段法对原始数据进行分帧操作，每一帧的长度N=4 096，帧移设置为512 帧，窗函数选用式（1）所示的海明窗。

然后对加窗后的数据进行短时傅里叶变换得到声纹信号能量谱图，即声纹信号时频谱图。该0.5 s声纹数据生成的时频谱图及其局部放大图见附录A图A1。由图可以看出：100、200、300 Hz 占据的能量比其他频率的能量大，这也符合变压器铁心振动噪声集中在低频段的机理。

1.2 Mel时频谱图

尽管时频谱图能够较完整地反映变压器铁心振动信号的时频特性，但是由于变压器铁心噪声的频率多集中在100～300 Hz 低频段［17］，而普通时频谱图的频谱响应范围过大，无法突出低频有效信息，因此本文考虑使用Mel时频谱图替代普通时频谱图。

Mel 时频谱图在语音识别领域能够很好地模拟人耳的听觉特性，由于人耳对低频变化比高频变化更敏感，因此Mel 时频谱图将原本的线性谱图转化为对数谱图，转换公式为：

式中：f为实际的频率；fMel为转换后的Mel频率。可知实际的频率越大，转换后就变得越平缓，更接近人耳的感受。因此本文采用Mel 时频谱图作为提取的二维特征图之一。

选取1.1 节中的0.5 s 声纹信号数据，按照1.1 节中所述方法生成时频谱图，并将Mel 滤波器组用于该时频谱图上。Mel 滤波器组是一个等高的三角滤波器组，每个滤波器的起始点在上一个滤波器的中点处，其对应的频率在Mel尺度上是线性的。Mel滤波器组的公式为：

式中：Hm(k)表示第m个滤波器的公式；f(m-1)、f(m)、f(m+1)分别为第m个滤波器的起始点、中间点和结束点。经滤波后得到的Mel 时频谱图见附录A图A2。

相较于普通时频谱图，Mel 时频谱图有效降低了高频区域，从25 kHz 降低至16 384 Hz，突出了低频段，符合变压器振动噪声的有效频率分布。

1.3 GAF时频谱图

虽然Mel 时频谱图语音识别领域有非常广泛的应用，但是由于其使用Mel 滤波器，尽管在低频段滤波器密集，门限值大，但由于其为三角形滤波，且滤波器数量不宜过多，因此仍有可能在低频段损失部分有效信息，如附录A 图A3 所示。为此，本文采用GAF变换对原始数据进行二次特征提取。

GAF 变换是结合坐标变换与格拉姆矩阵，实现将时间序列变换成图像的一种编码方式［18］。首先通过一个最小-最大定标器（min-max scaler）将原始数据归一化至［-1，1］范围内，计算公式为：

式中：X为采样点数据集；xi为采样点数据集中第i个采样点的数据；x͂i为采样点数据集中第i个采样点的数据进行归一化后的取值。

然后对归一化处理后的数据进行极坐标变换，考虑时间序列的值及其对应的时间戳，并将其表示为角度与半径的形式，在数学上可表示为：

式中：ϕi为角度变量；ri为半径变量；Ni为［-1，1］区间的等分数量。

最后选用和角关系和差角关系得到GASF 和GADF 二维时频谱图。选用1.1 节中所述的0.5 s 声纹信号作为原始数据，对其进行GAF 变换，分别选用GADF 与GASF 这2 种三角函数变换，得到的二维特征时频图见附录A图A4。

GAF 变换是直接在原始数据上进行操作，将时序信号的值存储在2 种时频谱图像素点的对角线上，且没有经过滤波处理，因此既能保留信号完整的信息，又能保持信号对于时间的依赖性，从而在一定程度上弥补Mel 时频谱图由于滤波造成的低频数据损失的问题。

2 特征融合

由前文可知，Mel 时频谱图可以较好地表示声纹信号的时域与频域关系。同时，对原始数据采用GAF 变换能够弥补Mel 时频谱图的低频缺失问题，因此本文将Mel时频谱图与GAF 时频谱融合形成新的二维特征时频谱图。

本文共设置60 %、80 %、100 % 这3 种变压器铁心松动情况，并对每种情况采集声纹信号。其中每种故障类型下，选取每0.5 s 的声纹数据生成Mel 时频谱图，同时将该0.5 s 中的数据作GAF 变换，得到GASF 与GADF 这2 种时频谱图。经过GAF 变换后得到的时频矩阵维度较大，而Mel 时频矩阵的维度为128×49，因此需要对两时频矩阵的维度进行处理后才可进行特征融合。

首先本文采用散乱点插值函数griddata 对2 种时频矩阵进行数据插值，将Mel 时频矩阵的维度扩充至400 × 400，同时将GAF 变换所得的2 种时频矩阵也分别调整至同等维度。然后将维度调整后的时频矩阵展开为一列，并通过转置将时频矩阵转换为一行。由于Mel 时频谱图与GASF、GADF 时频矩阵的数据范围为［-1，1］，因此再采用式（6）所示的mapminmax 函数将2 种时频矩阵中的数值同时归一化至［0，1］范围内。

式中：ymax=1；ymin=0；xmin、xmax分别为该矩阵中的最小和最大元素；x为选中元素。

归一化处理后将所得矩阵还原为原始时频矩阵形式。最后建造一个三维矩阵表示红-绿-蓝（redgreen-blue，RGB）图像的3 个通道，其中R 通道采用0.35 % 的还原后的Mel 时频矩阵，G 通道采用0.15 %的还原后的GASF 或GADF 时频矩阵，B 通道选取为0.5。3种工况下的Mel-GASF及Mel-GADF 特征融合时频谱图见附录A图A5。

3 ConvNeXt-T网络

ConvNeXt 网络由Facebook AI Research 和UC Berkeley 于2022 年1 月提出。ConvNeXt 网络是对卷积神经网络的一次全面革新。该网络对标的是近年来在计算机视觉（computer vision，CV）领域大放异彩的ViT（vision transformer）网络，如Swin Transformer 神经网络等［19］。通过一系列实验比对，在相同的计算速度（floating point operations per second，FLOPS）下，ConvNeXt网络相比传统卷积神经网络具有更高的准确率及更快的推理速度［20］。因此本文采用ConvNeXt 网络作为变压器铁心松动故障诊断的识别网络。ConvNeXt 网络分为T、S、B、L、XL 这5 个版本，本文采用ConvNeXt-T网络。

3.1 网络原理

受益于各种新型架构及优化策略，基于Transformer 架构的模型近年来相比卷积神经网络展示出更优异的效果。受此启发，ConvNeXt 网络也采用相同的优化策略，并显现出比Transformer 架构更高的准确率及更快的速度。ConvNeXt 网络的主要改进包括以下方面。

1）将训练ViT 的策略训练原始ResNet-50 网络模型，发现在数据集上的效果相比原始模型有大幅提升，并将此结果作为后续网络改进的Baseline。

2）Macro design 优化模块。在该部分中，Conv-NeXt 网络首先将原ResNet-50 网络中各卷积层堆叠的模块（block）数由原先的（3，4，6，3）改为（3，3，9，3）。然后将ResNet-50 网络中最初的卷积核大小为7、步距为2的下采样模块调整为卷积核大小为4、步距为4的patchify模块。

3）ResNeXt-ify 优化模块。在该部分中，Conv-NeXt 网络借鉴了ResNeXt 网络中的组卷积结构，并更突出地使用了depthwise 卷积，使组卷积的组（group）数与通道（channel）数量相等。

4）Inverted Bottleneck 优化模块。ConvNeXt 网络将ResNet 网络中的Bottleneck 改为Inverted Bottleneck，即将每个残差模块中的3 个卷积层输出channel数由原先的（384，96，384）改为（96，384，96）。

5）Large Kernel Size 优化模块。在该部分中，ConvNeXt 网络首先将depthwise 卷积模块的位置由原先的后置改为前置，位于1×1 卷积层之前。然后将depthwise卷积的卷积核大小由原先的3×3增大为7×7。

6）Micro Design 优化模块。在该部分中，Conv-NeXt 网络仿照Transformer，将原先的ReLU 激活函数和BN（Batch normalization）层分别改为GeLU 激活函数和LN（layer normalization）层，并在ConvNeXt Block 模块中使用更少的激活函数和LN 层。最后ConvNeXt 网络将原先的ResNet 网络中的双卷积层下采样模块改为单独下采样。

3.2 网络结构

对于不同版本的ConvNeXt 网络，其区别在于每一个阶段（stage）输入特征层的channel 数与每一个stage重复堆叠block的次数不同，本文采用ConvNeXt-T 神经网络，其channel 数与每一个stage 重复堆叠block 的次数分别为（96，192，384，768）和（3，3，9，3）。网络具体结构见附录B 图B1。由图可看出，ConvNeXt-T 网络首先将输入的RGB 三通道图片（输入尺寸为224×224×3）放入一个卷积核大小为4、步距为4 的卷积层，随后进入LN 层进行归一化处理，从而得到尺寸为56×56×96 的图像。接着将归一化处理后的图像放入连续3 组Downsample+ConvNeXt Block模块，其中：每个stage重复堆叠block的次数与channel 数如前文所述；每个ConvNeXt Block 模块包括3个stage，如附录B图B2所示；stage1为一个卷积核大小为7、步距为1、padding为3的卷积层加上LN层；stage2 为一个卷积核大小为1、步距为1 的卷积层加上GeLU 激活函数；stage3 为一个卷积核大小为1、步距为1 的卷积层加上Layer Scale 层及Drop Path 层。将最后一个ConvNeXt Block 模块输出的图片（尺寸为7×7×768）放入Global Average Pooling 层，再经过LN层归一化处理后放入线性（Linear）层，最后输出。

4 试验与结果分析

为研究Mel、Mel-GASF、Mel-GADF 这3 种时频谱图与ConvNeXt-T 网络作用时对变压器铁心松动故障的诊断效果。本文搭建了变压器铁心松动故障试验平台，并采集不同工况下变压器铁心的声纹信号。

4.1 数据集制作

试验的对象为一台S13-M-200／10 变压器，通过扭力扳手改变螺栓的预紧力来模拟3 种变压器铁心松动故障，即铁心100 % 松动（预紧力为0）、铁心80 % 松动（20 % 的额定预紧力）、铁心60 % 松动（40 %的额定预紧力）故障。同时在低压侧加入400 V 电压，变压器运行状态设置为空载运行。采用高精度电容式麦克风作为声纹传感器，对不同工况下的变压器噪声进行采集，采样频率为50 kHz，试验现场见附录B 图B3。不同工况下的变压器声纹频谱图见附录B 图B4。由图可以看出：不同工况下的声纹频率特征存在明显区别，具体表现为各特征频段的声压幅值不同。对每种工况采集16 组声纹数据，平均每组数据采集时间约为25～30 s，每隔0.5 s 生成1 张时频谱图。铁心60 % 松动（40 % 的额定预紧力）工况下，生成Mel、Mel-GASF、Mel-GADF 时频谱图各914 张，铁心80 % 松动（20 % 的额定预紧力）工况下生成686 张，铁心100 % 松动（预紧力为0）工况下生成985 张，并按照8∶1∶1 的比例划分为训练集、验证集及测试集。

4.2 时频谱图及网络训练效果

本节将3种时频谱图放入ConvNeXt-T网络进行训练，同时为了对比网络性能，将相同数据集放入ResNet-50、ResNeXt-50 网络一起训练，并将验证集精度、测试集准确率和训练损失作为判断网络性能的指标。设置ConNeXt-T 网络的初始学习率（learning rate）为0.000 5，批尺寸（batch_size）为16。

迁移学习能够利用数据、任务或模型之间的相似性，将在旧领域学习过的模型应用于新领域，从而达到更高的训练精度和更快的训练收敛速度，因此本文在训练过程中引用了迁移学习的核心内容，即加载预训练模型。通过该方法能够使网络的训练收敛速度更快，在更少的迭代（epoch）数下达到更高的识别精度。本文设置3种网络的epoch数为50。

4.2.1 时频谱图训练效果

将3种时频谱图依次放入ConvNeXt-T网络进行训练，每种时频谱图各有2 585 张，其中训练集时频谱为2 068 张，各时频谱图的验证集准确率与epoch数的关系如图1所示。

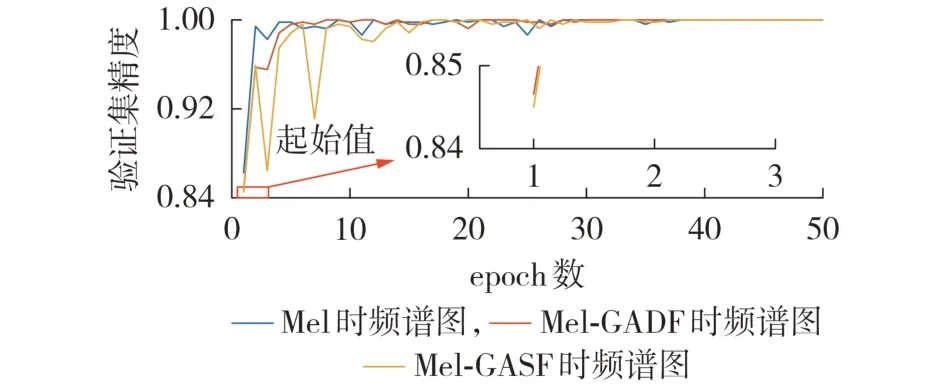
图1 3种时频谱图验证集精度Fig.1 Accuracy of validation set for three time spectrograms

由图1 可以看出：在ConvNeXt-T 网络中加载预训练模型后，各时频谱图的训练收敛速度都十分快，在2 — 5 个eopch 后便能达到90 % 以上的验证集精度；Mel 时频谱图在初始验证集精度上明显高于其他2 种时频谱图，但是在后续迭代过程中验证集精度有明显波动；Mel-GADF时频谱图在初始验证集精度上虽然没有Mel 时频谱图高，但在后续的迭代过程中验证集精度都维持在1 附近，几乎没有波动。经统计，Mel、Mel-GASF、Mel-GADF 时频谱图的测试集准确率分别为98.273 %、98.860% 、99.410 %。

3 种时频谱图的训练损失如图2 所示。由图可见：初始阶段训练损失呈现Mel-GASF＞Mel-GADF＞Mel 的规律；然而Mel-GADF 时频谱图的训练损失曲线下降得更快，在第4 个epoch 后就已经降至0.2 以下；在最后一个epoch 处，Mel、Mel-GASF、Mel-GADF时频谱图的训练损失分别为0.030、0.008、0.005。

图2 3种时频谱图训练损失Fig.2 Training loss of three time spectrograms

4.2.2 网络训练效果

由4.2.1 节可知，Mel-GADF 时频谱图相较于其他时频谱图在网络训练中有更好的效果。为了研究ConvNeXt-T 网络的性能，同时将Mel-GADF 时频谱图放入ResNet-50 与ResNeXt-50 网络中进行训练，设置epoch数为50，学习率为5×10-4，批尺寸为16，同样采用加载预训练模型的方法，在该种网络参数设置方式下，ResNet-50与ResNeXt-50网络对此训练集可以达到最好的训练效果。Mel-GADF 时频谱图在3 种网络中的验证集精度、训练损失分别如图3（a）、（b）所示。

图3 Mel-GADF时频谱图在3种网络中的验证集精度和训练损失Fig.3 Accuracy of validation set and training loss for Mel-GADF time spectrogram

由图3（a）可见：相较于ResNet-50、ResNeXt-50网络，ConvNeXt-T网络的初始验证集精度并不高，但是网络的收敛速度最快，验证集精度在3 个epoch 后超过另外2 个网络；在30 个epoch 后，ConvNeXt-T 网络的验证集精度几乎都维持在1，没有波动。经统计可知，该50 个epoch 中，ConvNeXt-T、ResNeXt-50、ResNet-50 网络的测试集准确率分别为99.410 %、98.533 %、98.933 %。

由图3（b）可见：尽管在初始阶段ConvNeXt-T 网络的训练损失较大，但是仍在1 以下，且其训练损失下降更快；在第3 个epoch 之后，ConvNeXt-T 网络的训练损失已低于ResNeXt-50、ResNet-50 网络；随着epoch数的增大，ConvNeXt-T网络的训练损失和波动减少，故其性能相对更稳定。

由上述分析可见，3种时频谱图中，Mel-GADF的验证集精度和测试集准确率相较于Mel、Mel-GASF时频谱图都存在明显优势，且训练损失更小；在对同一种时频谱图进行训练时，ConvNeXt-T 网络的性能优于ResNet-50与ResNeXt-50网络。

4.3 超参数调整

由4.2 节可以看出，将Mel-GADF 时频谱图与ConvNeXt-T 网络结合在测试集准确率上能达到最高，并表现出较快的训练损失下降率，但是在初始验证集精度及初始训练损失值上还有提升空间。因此本节对ConvNeXt-T网络中的批尺寸和学习率这2个超参数进行调整以找到最优的网络模型。

设置批尺寸sb为8、16、20，3 种批尺寸下的验证集精度、训练损失分别如图4（a）、（b）所示。

图4 3种批尺寸下的验证集精度和训练损失Fig.4 Accuracy of validation set and training loss for three values of sb

由图4（a）可以看出：当批尺寸为8 时，初始验证集精度明显高于另外2 种批尺寸下的初始验证集精度；随着epoch 数的增大，3 条折线都显示出相似的变化规律，虽然有所波动但是整体都在1 附近。经统计，批尺寸为8、16、20 时的测试集准确率分别为99.50 %、99.41 %、98.95 %。

由图4（b）可以看出：3 种批尺寸下的训练损失相差较小；当批尺寸为8 时，初始训练损失为0.814，小于另外2 种批尺寸下的初始训练损失；反观损失下降率方面，当批尺寸为20 时能展现出更快的损失下降率，且此时训练损失的波动更小；在最后一个epoch 处，批尺寸为8 时的训练损失值为0.001，小于批尺寸为16时的训练损失值0.005及批尺寸为20时的损失值0.004。

保持批尺寸为8 不变，分别设置学习率r1为5×10-3、5×10-4、5×10-5，3 种学习率下的验证集精度、训练损失分别如图5（a）、（b）所示。

图5 3种学习率下的验证集精度和训练损失Fig.5 Accuracy of validation set and training loss for three values of r1

由图5（a）可以看出，当学习率设置为5×10-4时，ConvNeXt-T网络不仅在初始验证集精度上有明显优势，而且在后续epoch数增加时也很少出现精度波动的情况。经统计，当学习率为5×10-3、5×10-4、5×10-5时，测试集准确率分别为93.25 %、99.50 %、98.85 %。

由图5（b）可以看出：尽管学习率为5×10-5时，初始训练损失值最小，为0.796，但随着epoch 数的增大，如epoch 数为35 — 50时，学习率为5×10-4时的训练损失值整体比学习率为5×10-5时的数值低，且波动更小；在最后一个epoch 处，学习率为5×10-4时的训练损失值为0.001，小于学习率为5×10-5时的训练损失值0.007 及学习率为5×10-3时的训练损失值0.07。

由此可得，ConvNeXt-T 网络的批尺寸和学习率分别为8和5×10-4时，网络对于本文设置的数据集可达到最佳训练效果。

4.4 准确率验证及模式对比

由4.3 节可知，当ConvNeXt-T 网络的批尺寸和学习率分别为8和5×10-4时，网络的验证集精度有所提升，训练损失波动也更小。本节将组合后的最佳训练网络再次与ResNet-50 和ResNeXt-50 网络进行对比，将3 种时频谱图放入3 种网络中，得到9 种组合方式，见附录C 表C1。由表可见，在9种组合方式下，基于Mel-GADF 时频谱图和ConvNeXt-T 网络的模型性能最佳：将初始验证集精度从普通Mel 时频谱图的87.50 % 提升至91.67 %，提升了4.17 个百分点；将平均损失从普通Mel 时频谱图的0.107 4 降低至0.060 6，降低了0.046 8；将测试集准确率从普通Mel 时频谱图的98.273 % 提升至99.500 %，提升了1.227个百分点。

同时本文还与另外2 种传统铁心故障辨别模式，即梅尔频率倒谱系数-卷积神经网络（Mel frequency cestrum coefficient-convolutional neural networks，MFCC-CNN）及梅尔频率倒谱系数-矢量量化（Mel frequency cestrum coefficient-vector quantization，MFCC-VQ）进行了对比，对比结果见附录C 表C2。由表可以看出，将Mel-GADF 时频谱图作为特征识别量时的测试集准确率高于将传统MFCC 作为特征量时的测试集准确率，且采用Mel-GADF 时频谱图时的平均迭代时间比传统MFCC-CNN 及MFCC-VQ 算法都短，因此将Mel-GADF 时频谱图作为特征识别量的故障识别性能更好。