基于电磁时间反演的VSC-HVDC系统架空线-电缆混合线路故障定位方法

2024-03-26张艳霞

电力自动化设备 2024年3期

张艳霞，李婷

（天津大学智能电网教育部重点实验室，天津 300072）

0 引言

直流输电系统因其输电容量大、距离远、节省输电走廊和能够实现非同步联网得到了广泛应用。为了满足直流输电跨越大水道、海峡以及美化市容等特殊需求，直流输电线路常采用架空线-电缆（下文简称线缆）混合线路。架空线和电缆的参数不同造成线路阻抗不均匀，导致传统的故障定位方法无法应用，研究适用于线缆混合直流输电线路的故障定位技术对于保障电力系统的正常运行、提高系统的供电可靠性具有重要意义。

目前，针对线缆混合直流输电线路的故障定位主要采用先确定故障区段、后在区段中定位的原理。文献［1］先通过测量故障初始行波到达线路两端的时间差区分故障区段，再通过故障距离与故障行波到达线路两端的时间关系进行区段内故障定位，定位精度取决于初始行波波头的识别。文献［2］在文献［1］的基础上，基于固有频率法对故障区段判定和故障定位结果进行校验，避免波头识别错误导致的定位错误，但只适用于两段式线缆混合直流输电线路。文献［3］基于文献［1］的故障区段判断方法，针对电压源型换流器高压直流输电（voltage source converter based high voltage direct current，VSC-HVDC）系统提出用罗果夫斯基线圈获取波头到达时间，为行波法在线缆混合直流输电线路故障定位的应用提供了新途径。文献［4］在模块化多电平换流器高压直流输电系统（modular multi-level converter based high voltage direct current，MMC-HVDC）系统的混合线路连接点加装测量点，利用罗果夫斯基线圈测取电流，依据电流形态谱特征判别故障区段并实现故障定位。文献［5］通过归一化故障后一段时间内的电压和电流小波能量，利用支持向量机的模式分类能力确定故障区段；再比较初始波头和第二次到达测量端的波头极性确定故障是在前半段还是后半段；最后利用波速与波头时间差的乘积进行故障定位，定位过程复杂。文献［6］利用人工神经网络的逼近和拟合能力，结合不同区段发生故障时的固有频率的特点，建立分层分布式神经网络模型实现线缆混合直流输电线路的故障定位，缺点是实际中难以获取大量故障样本。

电磁时间反演（electromagnetic time reversal，EMTR）理论［7］给直流线路故障定位带来新思路，目前主要应用于单一参数直流线路。EMTR 通过对测量点的电流进行时序反转得到反演电流，再建立原传输线方程的镜像空间，通过将反演电流注入镜像电路，基于故障点能量聚焦的特点找到故障位置。文献［8］提出利用特定频段的反演电流找寻能量最大的故障点，但该方法假定线路无损，影响了故障定位精度。文献［9］基于文献［8］研究了小波分解提取线路两端电流特定频段分量的方法，但其只适用于单一参数线路。文献［10］递进式论证了在不考虑反射波、考虑反射波和考虑混合参数的线路中利用EMTR 进行故障定位的可行性。然而，混合线路时间反演电路中的电流源表达式复杂，且需要假设每段线路的每点上发生故障以求出初始参数，在此基础上才能搜索出故障点，计算过程相对复杂。文献［11］针对分支和混合等复杂线路结构，先利用每条线路两端差流大于阈值确定故障区段，再对单端电流进行时间反演，求取能量最大的故障点，但该方法同样假定线路无损，故障定位精度受到影响。

本文提出一种适用于VSC-HVDC系统的线缆混合直流线路故障定位方法：利用故障附加网络线路两端的直流分量电流行进波构建故障区段判别函数，依据不同区段发生故障时的判别函数值判定故障区段；分析了EMTR 理论在故障定位中的可行性和故障电流特点，确定故障特征谐波，利用线路两端特征谐波的电流行进波构建时间反演电路，基于能量聚焦特性实现区段内故障定位。最后搭建仿真模型验证了本文所提故障定位方法的有效性。

1 利用线缆混合线路上的电流行进波实现故障区段判定

架空线和电缆各区段之间的电气量不连续。因此，线缆混合线路的故障定位通常采用先判定故障区段、后在区段内定位的方案。

单根长度为l的均匀传输线MN如图1所示。根据传输线方程，线路M侧的电压UM、电流IM和N侧的电压UN、电流IN可分解为正向行进波U+M、U+N、I+M、I+N和反向行进波U-M、U-N、I-M、I-N，如式（1）所示。

图1 单根均匀传输线示意图Fig.1 Schematic diagram of single uniform transmission line

式中：R0、G0、L0和C0分别为均匀传输线MN单位长度的电阻、电导、电感和电容；Z为线路波阻抗；γ为传输常数，表征电压行进波和电流行进波沿线传输的幅值衰减和相位移动。对于直流系统而言，正常运行和故障稳态后的电压、电流主成分为直流分量，则，说明直流分量经输电线路传输时只存在幅值衰减，本章采用直流分量行进波进行分析。

三段式线缆混合线路MN如附录A 图A1 所示。图中：MC、TN段为架空线路；CT段为电缆。每段线路的首、末端电流行进波满足式（3）所示的关系。

式中：lMC、lCT和lTN分别为MC、CT和TN段的长度；和为各段线路的正向和反向电流行进波，下标1、2 分别表示电流位于架空线、电缆，后同；ZL和ZC分别为架空线和电缆的波阻抗；γL和γC分别为架空线和电缆的传输常数；RL、GL和RC、GC分别为架空线和电缆单位长度的电阻、电导。

正常情况下，流入M侧和N侧的电流行进波I-M和I+N的比值为常数，只与线缆混合线路的结构和参数相关。当故障发生在不同区段时，I-M与I+N的比值会随故障点的位置变化。因此，本文利用不同区段故障下故障分量中的行进波比值定位故障区段，具体如下。

1）架空线路MC发生故障。

架空线路MC发生故障时的故障附加网络如图2所示。图中：UC、UT分别为故障附加网络中连接点C、T的电压；IF为故障点电流；ZM、ZN分别为M、N侧系统等效阻抗；INC1和INC2分别为从架空线MC流入连接点C的故障电流和从连接点C流入电缆CT的故障电流；INT1和INT2分别为从连接点T流入架空线TN的故障电流和从电缆CT流入连接点T的故障电流，故障点F的电压故障分量ΔUF［12］产生的电流故障分量IMF和ICF分别流向故障点两侧；IM，f和IN，f分别为M和N侧的电流故障分量；I+M，f、I-M，f和I+N，f、I-N，f分别为IM，f和IN，f的正、反向行进波；UM，f和UN，f分别为M和N侧的电压故障分量。

图2 架空线路MC发生故障时的故障附加网络Fig.2 Fault additional network when fault occurs in overhead line

定义区段判别函数P如式（4）所示。

首先推导得到I-M，f的表达式如式（5）所示，具体推导过程见附录A式（A1）—（A6）。

式中：ρM=(ZM-ZL)/(ZM+ZL)；lMF为线路MF的长度。

然后推导得到I+N，f的表达式如式（6）所示，具体推导过程见附录A式（A7）—（A16）。

式中：lCF为线路CF的长度。

将式（5）、（6）代入式（4）中可得：

将P对lCF求导可得：

因|ρM|=|(ZM-ZL)/(ZM+ZL)|＜1、|ρN|=|(ZN-ZL) ÷(ZN+ZL)|＜1 、|ρL|=|(ZL-ZC)/(ZL+ZC)|＜1，则有：

则dP/dlCF＞0，即P是关于lCF的增函数。当故障发生在连接点C时，lCF=0，P取得最小值PC，如式（11）所示。

因此，架空线路MC发生故障时满足：

2）电缆CT发生故障。

电缆CT发生故障时，P的表达式如式（13）所示，具体推导过程与架空线路MC发生故障时类似，本文不再赘述。

同理可得，电缆CT发生故障时，P为lTF的增函数。当故障发生在连接点T时，P取得最小值PT，如式（14）所示。

当故障发生在连接点C时，P取最大值PC。

因此，电缆CT发生故障时满足：

3）架空线路TN发生故障。

架空线路TN发生故障时，P的表达式如式（16）所示，具体推导过程与架空线路MC发生故障时类似，本文不再赘述。

式中：lNF为架空线路NF的长度。

同理可得，架空线路TN发生故障时，P是关于lNF的增函数。故障发生在连接点T时，lNF=lNT，P取最大值PT（见式（14））。

因此，架空线路TN段发生故障时满足：

综上所述，故障区段与故障区段判别函数的对应关系如表1所示，由表1可实现故障区段判定。理论上，双端数据不同步只影响两端正弦信号的相位差，不影响其幅值。而本文故障区段判别利用的是线缆混合直流线路两端的直流量，因此不受双端数据不同步的影响。

表1 故障区段与故障区段判别函数的对应关系Table 1 Corresponding relationship between fault segment and fault segment decision function

2 基于特征谐波和EMTR 进行区段内故障定位

2.1 VSC-HVDC系统直流输电线路的故障特征谐波

根据文献［13］和文献［14］，当VSC-HVDC 系统直流线路发生单极接地故障时，故障过程经历电容放电、交流侧馈入暂态和交流侧馈入稳态3 个阶段。电容放电阶段的故障电流包含衰减振荡或衰减非周期分量；交流侧馈入暂态阶段的故障电流包含直流、衰减振荡和衰减非周期分量；在交流侧馈入稳态阶段，绝缘栅双极型晶体管闭锁，换流站等效为三相桥式不控整流电路，故障电流包含直流分量和6 次谐波，且6 次谐波在所有谐波中幅值最大。当直流线路发生双极故障时，故障过程经历电容放电、二极管续流和交流侧馈入3 个阶段，其中电容放电、二极管续流与单极接地故障相同。可见，无论是单极接地故障还是双极故障都会进入交流馈入阶段，该阶段包含6 次谐波且幅值较大，其可以看作VSC-HVDC系统直流线路故障的特征谐波。因此，本文选取流入M侧和N侧电流行进波中的6 次谐波分量和，对其进行时间反演并构建镜像的时间反演电路进行区段内故障定位。

2.2 基于EMTR进行故障定位的可行性分析

EMTR 的核心和基础是对电磁波进行时间的反转。该反转不是时间的倒流，而是将时域信号进行逆处理并传回系统，即改变时间轴方向t→-t。设电流i(t)所处的时间区间为[0，T]，将其进行时间反转，并将时间向后平移T以保证被测信号和时间反转信号在同一个时间窗中，从而形成反演后的电流i(T-t)，反演过程见附录B图B1。

对于无损传输线，其电报方程为：

式中：z为电磁波的传输距离。

将电流消去后得到电压方程为：

将u(z，-t)代入式（19），并令τ=-t，则有：

由式（20）可知，u(z，-t)仍然为电报方程的解，证明时间反演信号仍可在无损线路中传播。在时域反转的基础上，对函数自变量进行时域平移得u(z，-t+T)，其仍为无损传输线的解，说明传输线方程具有时间反演不变性。

故障附加网络中的电流、电压也是电磁波，同样也按照电报方程传输。因此，对故障附加网络的电流进行时间反演构建时间反演电流源，其在镜像反演线路中的传播过程具有时间反演不变性，得到的解也为输电线路的解。可知，基于EMTR 进行故障定位具有可行性。

2.3 EMTR反演电路的建立

EMTR 反演电路包括镜像反演线路和时间反演的电流源。

1）建立镜像反演线路。根据文献［15］，将反演电路的电阻和电导设为原线路的电阻和电导相反数、电感和电容与原线路的电感和电容相同时，利用EMTR 进行故障定位的结果最精确。将架空线路和电缆的6次谐波（ω=600 π rad／s）单位长度电阻、电导、电感、电容的频域参数分别记为-RL，6、-GL，6、LL，6、CL，6和-RC，6、-GC，6、LC，6、CC，6，则6 次谐波下的传输常数γ′L，6和γ′C，6分别为原电路传输常数γL，6和γC，6共轭的相反数，即：

式中：“*”表示对参数取共轭。

得到6 次谐波的EMTR 电路见附录B 图B2（a），时间反演电流源为IMset和INset。

2）确定时间反演电流源。以MC段发生故障为例，其6次谐波网络见附录B图B2（b）。

时间反演电流源IMset和INset的表达式如式（22）所示，具体推导过程如附录B式（B1）—（B3）所示。

式中：UM，6、UN，6和IM，6、IN，6分别为线路M、N侧电压和电流的6次谐波分量；ZL，6、ZC，6分别为架空线和电缆的6次谐波波阻抗；T0=40 ms。

交流馈入阶段的电流除了含有直流分量和6、12、18 次谐波分量外，还含有其他次谐波。本文采用文献［16］提出的自适应特征尺度分解算法，通过将自适应特征尺度分解与改进广义局部频率解调方法相结合，自适应地将要提取的分量准确提取出来。利用该算法提取的6 次谐波电流标幺值如附录B 图B3所示。

2.4 区段内故障定位

以判别出故障发生在架空线路MC的情况为例，假设故障点F距M的距离为x，点M的反演电流源为IMset，由点N反演电流源INset推导出点C的反演电流为：

因此，点F两侧的电流IMx和ICx为：

将架空线路和电缆的传输常数表示为：

式中：αL、αC和βL、βC分别为γL，6、γC，6的实部和虚部。

由故障点发出的时间反演信号会在故障点产生能量聚焦现象［7］。因此，反演电路中故障点的电流数值最大，故障定位方程可写为：

将式（25）代入（26），并用极坐标表示为：

式中：|IMset|、|INset|和φMset、φNset分别为IMset、INset的幅值和相角。

故障定位就是求解f(x)最大值问题。|IMset|、|INset|、φMset和φNset均为已知量，f(x)是只包含1 个变量x的非线性函数，可以利用粒子群优化算法进行求解，具体说明见附录C。

下面分析双端数据不同步对区段内故障定位的影响。设M侧时钟为参考时间，N侧时钟与其误差为Δt0，则两侧对应的6 次谐波相角差Δφ0=12πfΔt0(f=50 Hz)，N侧实际测得的相量变为I′Nset=INsete-jΔφ0，故障定位方程变为：

根据式（27）可得：

式中：Φ=φMset-φNset+βLlTN+βClCT+βLlMC。

实际工程中Δt0约为±2 µs，对应的6 次谐波相角差Δφ0=12π×50×2×10-6=0.001 2π，sin 0.001 2π≈0，将其代入式（29）得：

式（30）与式（27）相比，仅等号右侧第3 项的初值不同，且两者之比为0.999 993，粒子群优化算法中二者的适应度函数相同，下次迭代的粒子位置也一致。因此，本文算法的故障定位精度受两端同步误差影响较小。

本文故障定位原理利用的是交流馈入稳态阶段的电气量。如果稳态阶段前主保护动作，会由于提取6 次谐波的时间窗不够长而影响故障定位的精度。实际的故障定位装置中，可以考虑与其他定位方法结合来弥补。

3 基于EMTR 原理的VSC-HVDC 系统混合线路故障定位步骤

故障定位整体流程见附录D图D1，说明如下。

1）利用故障后线路两侧正极和负极故障电压、电流，计算出线模分量如式（31）所示。

2）分别提取出uM，f、iM，f、uN，f、iN，f中的直流分量UM，f、IM，f、UN，f、IN，f和6次谐波分量UM，6、IM，6、UN，6、IN，6。

3）故障区段判定。利用线路两侧的直流分量求出区段判别函数P的值，并依照表1判定故障区段。

4）构建时间反演电流源IMset和INset，然后计算故障区段两端点的反演电流：若故障发生在MC段，则计算连接点C的反演电流ICset=INsete(αL-jβL)lTN+(αC-jβC)lCT；若故障发生在CT段，则计算连接点C的反演电流ICset=IMsete(αL-jβL)lMC和连接点T的反演电流ITset=INsete(αL-jβL)lTN；若故障发生在TN段，则计算点T的反演电流ITset=IMsete(αL-jβL)lMC+(αC-jβC)lCT。根据两端点反演电流求出故障点F的反演电流，并构建如式（26）所示的故障定位方程。

5）基于粒子群优化算法求解故障距离。

4 仿真验证

本文在PSCAD／EMTDC 中搭建VSC-HVDC 系统验证所提故障定位方法的有效性［17］，系统接线如附录E 图E1 所示，主要参数如下：系统容量为200 MV·A，换流变压器变比为230 kV／110 kV，直流额定电压为±100 kV，换流站采用两电平VSC 型。线路采用图2 所示的三段式线缆混合结构，仿真采用相域模型，架空线MC、TN的长度分别为50、40 km，电缆CT的长度为30 km，线路具体参数见附录E 表E1。采样频率取为4 kHz。利用模型参数计算得到的区段判别函数P如表2所示。

表2 故障区段函数的计算结果Table 2 Calculation results of fault segment decision function

距点M出口10 km处发生经30 Ω过渡电阻的单极接地故障时，点M、N的测量电流和电压的标幺值如图3（a）所示。图中虚线框内为2.040～2.042 s时间段内的局部放大波形。电流的直流分量从测量电流中滤除特征谐波得到，6 次谐波分量利用文献［16］所提算法进行提取。点M的正极电流中直流和6 次谐波分量的标幺值如图3（b）所示。

图3 仿真波形Fig.3 Simulative waveforms

经计算可得P=12.014 2＞1.300 5，判定架空线MC故障。故障定位结果lMF=10.984 2 km，相对误差，具体的故障定位过程见附录F。

将本文算法与文献［1］所提的双端行波法进行对比，双端行波法采样频率设为1 MHz，利用小波模极大值［18］提取图3中故障电流模量行波到达点M、N的时刻tM和tN如图4所示。

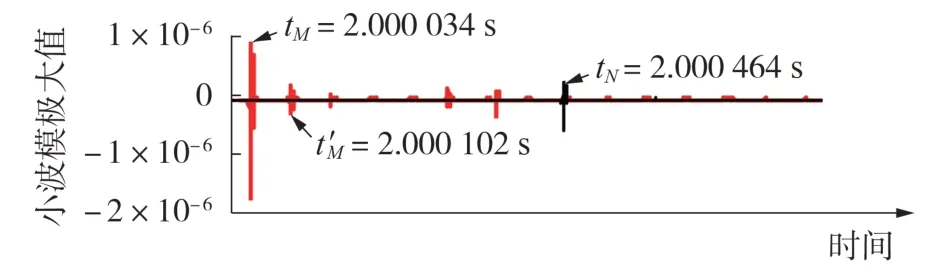
图4 由小波模极大值计算得到的行波到达点M、N的时刻Fig.4 Time when traveling waves reach to Point M and N calculated by wavelet modulus maximum

由图4 得ΔtMN=tM-tN=-0.000 430 s，由仿真模型参数得架空线波速vL=2.94×105km／s，电缆波速vC=1.56×105km／s，因此故障距离为：

可见，正确识别波头的情况下，故障定位精度非常高。

设点M测量装置未能正确识别波头，将故障点反射波头作为初始波头，则Δt′MN=t′M-tN=-0.000 362 s，求得的故障距离为：

由式（33）可知，如果故障初始行波波头识别错误，则双端行波法的故障定位结果将是错误的。对比发现，本文故障定位方法虽然精度不及文献［1］所提方法，但稳定性好且满足实际工程要求。

本文在每段架空线设置3 个故障点、在电缆设置2 个故障点，依据故障区段判别函数P能准确判断故障区段。表3、4 分别为不同故障条件下的故障定位结果。表中：Rf为过渡电阻。仿真结果表明，本文故障定位方法能满足实际工程要求。

表3 单极故障定位结果Table 3 Fault location results of unipolar fault

表4 双极短路故障定位结果Table 4 Fault location results of bipolar fault

针对存在同步误差的情况进行仿真验证。设N侧时钟比M侧慢2 个采样点，即在本文中时间上慢0.5 ms。利用M、N侧的测量电压、电流计算得到的区段判别函数P=12.027 1＞1.300 5，与同步采样情况下P=12.014 2 相比变化不大，仍然判断MC段发生故障。故障定位结果为lMF=11.179 4 km，相对误差