基于调制系数最优法的TLDMC-PMSM新型直接转矩控制
2024-03-26程启明程尹曼岳秉言
程启明,刘 科,程尹曼,张 昕,岳秉言
(1.上海电力大学 自动化工程学院 上海市电站自动化技术重点实验室,上海 200090;2.上海电力公司 市北供电分公司,上海 200041)
0 引言
永磁同步电机(permanent magnet synchronous motor,PMSM)以其高效率、高功率密度、动态响应快、结构简单等优点,在工业领域得到广泛关注与应用,同时也推动着PMSM控制理论的快速发展[1]。
直接转矩控制(direct torque control,DTC)通过磁链和电磁转矩表达式对其直接计算,然后采用Bang-Bang 控制产生脉宽调制(pulse width modulation,PWM)信号来控制电磁转矩和磁链,实现转速和转矩的优良控制,所以不需要复杂的坐标变换和电流控制器就能够实现快速、精确的转矩控制响应[2]。但是,传统DTC 存在一些不足,其最主要的缺陷就是转矩和磁链脉动较大,并且系统的鲁棒性弱。为此,有学者提出了具有更多控制矢量的新型变换器和新型速度、转矩环的控制算法来降低波形脉动,提高系统的鲁棒性。
通过新型变换器来改进上述控制算法的缺点是较为有效的,常见的新型变换器有矩阵变换器(matrix converter,MC)[3]、三电平直接矩阵变换器(threelevel direct matrix converter,TLDMC)[4]、模块化多电平MC[5]、Z 源/准Z 源MC[6]等。其中:MC 能量可实现双向流动,这样可以实现四象限运行,输入、输出波形都为正弦,畸变率小,可提高系统的运行稳定性,且功率因数可调[7];TLDMC[8]是在MC 的基础上发展而来的,相比MC 而言,它进一步增加了有效矢量的个数,降低了输出波形的畸变率和共模电压,提高了动态响应和输出电压,相比三电平间接MC 而言,它将逆变级和整流级调制结合在一起,减少了调制计算复杂度和绝缘栅双极型晶体管(insulated-gate bipolar transistor,IGBT)的数量,极大降低了开关损耗。
为了结合PMSM、DTC、MC 三者的优势,有学者将DTC 结合空间矢量脉宽调制(space vector pulse width modulation,SVPWM)应用于MC-PMSM 系统中,产生了MC-PMSM-DTC 系统[9],此系统有效提高了电机的转矩和转速动态响应速度。基于此,文献[10]利用评价函数分析MC 电压矢量对转矩和磁链的不同作用并提出划分主从矢量的方法;文献[11]提出一种基于占空比控制的方法;文献[12]用基于SVPWM 的DTC 方法,根据控制算法生成参考电压矢量,然后使用SVPWM进行合成,达到了期望目标,但该方法增加了计算和控制的复杂度;文献[13-14]采用模型预测转矩控制方法,在传统DTC 的基础上通过成本函数得到期望的电压矢量,但是该方法谐波大、计算复杂度高;文献[15-16]在传统矢量控制和DTC 的基础上,将两者优势结合,提出超螺旋DTC,将其通过逆变器来控制PMSM,减少了计算量,提高了动态响应和鲁棒性,但控制器有效矢量少会造成控制精度低,使得电机转动脉动大,影响了电机运行状态。总之,对于采用DTC 的PMSM 的控制算法而言,还存在电机各个参数的波动大、动态响应慢、鲁棒性弱、启动时高转矩作用时间长等缺点。
为了解决上述问题,首先,采用TLDMC 替换两电平MC,增加了有效矢量的数目,减少了波形畸变率,提升了电机运行的平稳性;然后,对传统DTC 的转速、转矩磁链环的控制方法进行了改进,结合Aire Levant 提出的高阶滑模控制思想[17],通过将不连续项放在滑模面的高阶导数中,使得低阶滑模面从本质上消除了抖振,既保留了传统滑模的优点又克服了传统滑模的缺陷[18-19],提出了新型直接转矩控制(new direct torque control,NDTC)方法,即转速环通过复叠式螺旋滑模控制(cascade spiral sliding mode control,CSSMC)、转矩磁链环通过超螺旋滑模直接转矩控制(super twisting sliding mode control-direct torque control,STSMC-DTC)来替换传统的比例积分(proportional integral,PI)控制和DTC,提高控制精度和系统鲁棒性,减少波形脉动,加快动态响应,从而克服启动时高转矩作用时间长的弊端;其次,为了更好地减小转矩磁链脉动,将每个周期的转矩磁链误差通过调制系数最优法(modulation coefficient optimization method,MCOM)输出来控制“虚拟逆变级”的有效占空比,进一步减小电机的转矩磁链脉动,使得电机更加平稳运行。综上所述,本文提出了基于MCOM 的TLDMC-PMSM-NDTC 系统,该系统对于电机运行平稳性、动态响应、各参数脉动、系统鲁棒性都有着非常明显的提升;最后,通过软件仿真和硬件实验说明本文所提方法的有效性与优势。
1 MC-PMSM-DTC系统存在的问题
MC-PMSM-DTC 系统的结构框图见附录A 图A1。该系统首先利用定子磁链Cψ、电磁转矩滞环比较器的输出值CT来判断出磁链和转矩的增减性,其次在开关表中选择对应的电压矢量作用于MC,然后通过输出电压、电流来计算出转矩和磁链的预测值,通过反馈预测值与标准值进行比较判断出转矩和磁链的增减性,进而达到转矩和磁链的控制。DTC 利用Bang-Bang 控制产生PWM 信号来调制MC 并控制PMSM,它对于电机的参数依赖性特别强,电机的参数稍有变化时,就会对控制效果产生影响,并且由于MC 的有效矢量较少,搭配DTC 更会增大转矩和磁链脉动,这对于电机的运行极为不利。
本文提出基于MCOM 的TLDMC-PMSM-NDTC系统来解决上述问题。首先,将常规MC改为TLDMC,增加有效矢量个数,在配合DTC 时能更加精确控制,提高波形平滑度;其次,将传统DTC 改为NDTC(即CSSMC-STSMC-DTC),提高电机转速转矩的动态调整时间,增强系统的鲁棒性;然后,将MCOM 引入TLDMC 调制中,通过使用电机的转矩和磁链误差反馈值来调整占空比进而减小转矩和磁链的脉动。
2 基于MCOM的TLDMC-PMSM-NDTC系统
图1为基于MCOM 的TLDMC-PMSM-NDTC系统的结构框图。该系统主要由TLDMC、PMSM 以及TLDMC 调制与控制3 个部分构成。其中:TLDMC 完成电能的变化和能量的传输,实现对PMSM 转矩、转速的控制;TLDMC 调制与控制分为整流级和逆变级2个部分,在逆变级中对PMSM 的转矩和磁链进行直接控制,进而实现对PMSM 转速的控制。上述控制算法结合了SVPWM 和CSSMC-STSMC-DTC,不仅实现了转速的快速跟踪,而且很大程度上降低了转矩和磁链的波动。图1 中:UA、UB、UC和iA、iB、iC分别为TLDMC输出三相电压和电流;、ωr分别为PMSM 的参考转速、反馈转速;、Te分别为PMSM 的参考转矩、反馈转矩;、φs分别为PMSM 的参考磁链、反馈磁链;ud、uq分别为d、q轴电压分量;uα、uβ分别为α、β轴电压分量分别为转矩、磁链的参考值与反馈值之差的绝对值;mc、mv分别为输入相电流空间矢量调制系数、输出相电压的SVPWM 系数;Ko为调制系数最优值;Iref为三相参考电流值;Iα、Iβ分别为参考电流αβ坐标系下α、β轴的电流值。
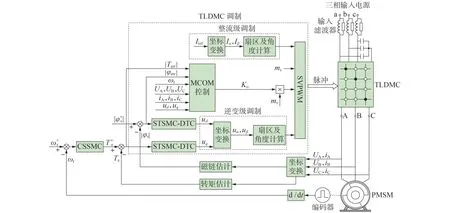
图1 TLDMC-PMSM-NDTC系统结构框图Fig.1 Structure block diagram of TLDMC-PMSM-NDTC system
2.1 TLDMC原理及调制
文献[7]对MC进行改进,将输入滤波器中点z连接至三相输出端,提出了TLDMC,其结构框图见图2。图中:Ua0、Ub0、Uc0和iˉa、iˉb、iˉc分别为三相电压源的输入电压和滤除高次谐波后的状态平均值的电流;Lfa、Lfb、Lfc和Cfa、Cfb、Cfc分别为三相输入LC滤波器的滤波电感和滤波电容;Ua、Ub、Uc和ia、ib、ic分别为TLDMC的三相输入电压和电流;Uz和iz分别为z 相电压和电流;Sjk为双向开关,j={A,B,C},k={a,b,c,z}。
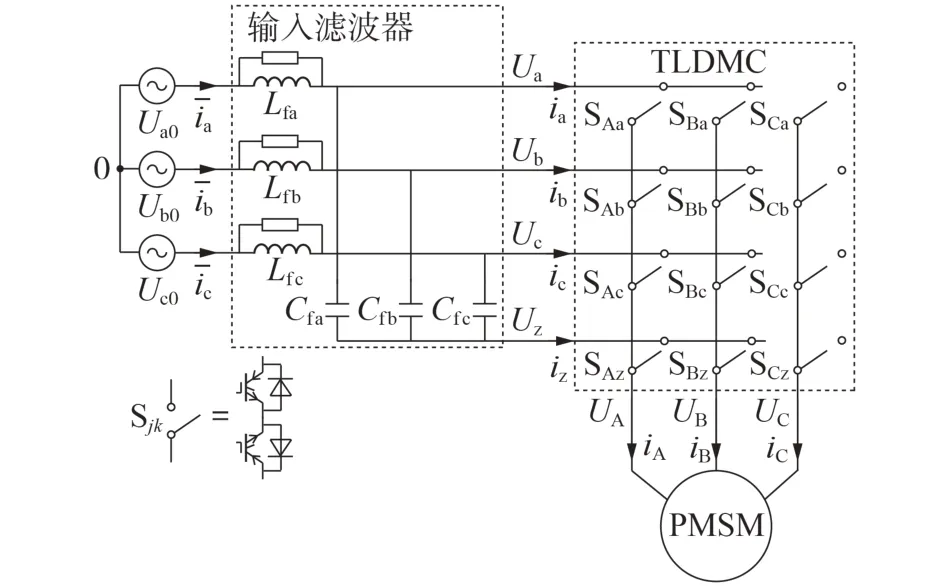
图2 TLDMC-PMSM系统结构框图Fig.2 Structure block diagram of TLDMC-PMSM
由图2可知,TLDMC的输出、输入电压和电流的关系式为:
式中:S(t)为TLDMC 的传输矩阵;Sjk为Sjk的开关状态,导通时取值为1,关断时取值为0;ui为输入电压向量;io为输出电流向量。
从式(1)、(2)可以看出,相比MC,TLDMC 的电压、电流多了z相,所以需要对iz进行平衡控制,保证其状态局部平均值为0,从而抑制Uz的偏移,使其基本维持零电位,能够降低输出电压含有的高频谐波。
为了大幅降低开关频率和开关损耗,同时能获得最大的电压利用率,可在对TLDMC 进行SVPWM时将每个扇区的零矢量消除,“虚拟整流级”的调制矢量轨迹图见附录A 图A2,在电流旋转至每个扇区时,由相邻2 个有效矢量合成,实现“虚拟整流级”的调制。由图A2 可得“虚拟整流级”的电流平均值ip,avg、电压平均值Upn,avg分别为:
式中:Iom为输出相电流的基波幅值;Uim为输入相电压的基波幅值;Pin为输入功率值;ωi为输入频率;φi为输入电压相位差;φo为输出电流相位差。
由于mc为最大值1,且“虚拟整流级”在每个扇区时是由相邻的2个矢量(定义为iμ、iv)合成,所以根据占空比调整规则可以得到合成电流的2 个分量占空比Dμ、Dv。
TLDMC 的“虚拟逆变级”存在33=27 种开关状态,这27 种开关状态对应的矢量以及不同开关状态产生的电流的大小及方向见附录A 图A3。27 种开关状态会合成不同幅值的矢量,计算这些矢量的幅值和相角并将这些矢量分为大矢量、中矢量和小矢量。以第1 扇区为例划分构成的虚拟空间矢量图见附录A 图A4。可以计算得到图A4 中矢量的幅值、相角和z 相电流iz见附录A 表A1。由表可知,iz为0,起到了抑制电压偏移的作用。在得到中点电流平均值为0 的新虚拟矢量后,需对虚拟矢量的占空比进行计算,以第1 扇区为例,得到各个矢量占空比大小见表1。表中:N为小扇区的编号;dx、dy和dz为小扇区所对应的最近3 个虚拟矢量的占空比;θsv为UoPhref在当前扇区中的位置,取值范围为[0,π/3];M为经过修正后的输出相电压调制系数,表达式见式(5)。

表1 矢量占空比Table 1 Vector duty cycle
式中:Uom为输出相电压的基波幅值。
同理可得其他扇区的占空比,完成“虚拟逆变级”调制,然后将“虚拟整流级”和“虚拟逆变级”结合起来的占空比进行计算,规划每个扇区的脉宽分布,实现对TLDMC的SVPWM。
2.2 PMSM转速和转矩调节的新型控制方法
图1 中,在实现TLDMC 的SVPWM 基础上,本文提出了NDTC 以实现对PMSM 转速和转矩的控制。与传统DTC 的PMSM 相比,该控制方法可以很好地抑制转矩和磁链的波动,提高转速的动态响应,增强系统的鲁棒性。
2.2.1 CSSMC算法
1)CSSMC原理。
CSSMC[16]是在常规滑模控制(sliding mode control,SMC)上进行多次迭代,将二阶滑模进行叠加,将线性和非线性进行组合叠加,这样不仅增强了系统的鲁棒性,使得系统稳定性得到了质的飞跃,而且加快了系统的响应速度。本文将CSSMC 引入电机转速控制上,能够缩短调整时间,减弱电磁转矩脉动,从而使波形更加平滑。
动态系统可描述为:
式中:P1(s)和P2(s)分别为系统的一次控制与二次控制部分;f为正数常量;A、B为调节系数;ṗ(t)为外部扰动;x为状态变化量;y为控制系统的输出;双曲正切函数tanhs=(eεs-e-εs)/(eεs+e-εs),其中ε为斜率因子,通过调整ε值来改变双曲正切函数在原点附近的斜率。
要想使系统趋于稳定(即在有限时间内收敛到原点),需满足如下条件:
式中:δ为扰动的边界值,表示动态系统中扰动的值是有界的,不管δ取任何值,满足式(7)的条件下系统都是稳定的。
输出函数表达式为:
式中:A1、B1为未知待求函数。因为对于一个系统的输出数学模型而言,除了自身要控制的参数外,其余的参数在有限时间内均收敛,所以A1、B1函数所得值一定是有界的,则存在正数A1M、B1m、B1M,使得对任意的y、x有:
结合式(9)可得CSSMC算法为:
2)复叠式螺旋滑模控制器设计。
本文首次把CSSMC 算法引入PMSM 控制中。表贴式PMSM的电磁转矩Te为:
式中:θ为位置角;Ld和Lq分别为定子电感的d、q轴分量,表贴式PMSM 中Ld=Lq;φf为永磁体磁链;p为极对数。
对式(11)求2阶导数有:
由式(10)可得PMSM的CSSMC算法为::
式中:Te*为电磁转矩的参考值;sω为转速的参考值与实际值的差值。
结合式(8)、(12)可以求出电磁转矩2 阶导数的A1、B1值,然后结合式(11)、(13),就可得出A、B、f值。通过调节这3个参数值来使CSSMC的控制效果达到最优,使PMSM 转速调节时间变短,且PMSM 转矩脉动变小,满足电机控制的理想结果。CSSMC 算法在常规SMC 基础上,增强了系统的鲁棒性,在面对高扰动干扰时系统也能保持优良的运行状态。
2.2.2 STSMC-DTC算法设计
STSMC-DTC 算法的原理推导公式见附录B 式(B1)—(B5),设计过程的公式推导见附录B 式(B6)—(B14)。本文将STSMC 引入PMSM 的DTC中,将电磁转矩、磁链的差值赋给s=φs*-φs=Te*-Te,然后对电磁转矩和磁链进行直接控制,采用STSMC 减少了转矩波动、提高了系统鲁棒性,相比采用DTC,直接将usd、usq作为控制目标,通过坐标变换进而实现“虚拟逆变级”的调制,结合“虚拟整流级”调制完成了TLDMC 的SVPWM,不仅增加了有效矢量数使得转速波动小,而且引入STSMC-DTC 对电磁转矩、磁链直接控制使PMSM的控制效果、动态响应更好。
2.3 MCOM控制
将CSSMC、STSMC-DTC 和SVPWM 相 结 合 对TLDMC 进行调制实现对PMSM 转速、转矩的控制。虽然STSMC-DTC 是对转矩和磁链直接控制,一定程度上可以降低转速和转矩波动以提高动态响应速度,但STSMC-DTC 输出的ud、uq直接连接至“虚拟逆变级”端,转矩和磁链的微小波动都会引起ud、uq的直接波动,转矩和磁链的反馈值会逐渐偏离参考值,进而影响整个TLDMC的SVPWM性能。
为此,本文进一步提出了MCOM 来解决转矩、磁链直接控制ud、uq引起的转矩、磁链反馈值逐渐偏离参考值问题,通过MCOM 控制将转矩、磁链参考值和反馈值的综合误差最小点来调整调制系数M,进而调整最优“虚拟逆变级”的占空比大小,这样可以很大程度上降低转矩、磁链的波动,使得PMSM 能够稳定运行,延长电机的使用寿命。
由式(11)可得:
式中:Te(k)为当前周期的电磁转矩;iq(k)为当前周期的输出电流q轴电流分量。
PMSM的q轴电流为:
式中:Rs为定子电阻;ωe为转子电角速度;id和iq分别为输出电流的d、q轴分量。
将式(15)离散化后可得:
式中:iq(k+1)为当前周期控制结束时的输出电流q轴分量;Ts为控制周期;id(k)为当前周期的输出电流d轴分量。
将式(11)、附录B 式(B10)离散化后,代入式(16)可得:
式中:us(k)、is(k)和φs(k)分别为当前周期的电压、电流和磁链;uq(k)为当前周期磁链和电磁转矩误差引起的实际q轴电压分量值;φs(k+1)、Te(k+1)分别为当前周期控制结束时的磁链和电磁转矩。
假设磁链和电磁转矩误差所引起的电压波动为原来电压的K倍,则:
式中:K为波动系数;ud(k)为当前周期磁链和电磁转矩误差引起的实际d轴电压分量值;ude(k)、uqe(k)分别为当前周期不考虑磁链和电磁转矩误差所引起的理想电压use(k)的d、q轴分量值。
将式(19)代入式(17)、(18)中整理可得:
则磁链转矩误差E(k)的综合关系式为:
因为E(k)>0,所以对式(21)求导等于0,可求出式(21)的最小值点,且此处求出的最小值点为波动系数K,K值为:
然后将求出波动系数的倒数与mv相乘来调节调制系数M,使得占空比达到最优,降低转矩和磁链的脉动。
由表1 可以看出占空比与调制系数M成正比,由式(22)、(23)可以看出当磁链和转矩误差变大时,K值会随之变大,而调制系数M会减小,随之“虚拟逆变级”有效矢量占空比也会减少,这样就可以解决由于电磁转矩和磁链误差总和所引起的有效矢量不断增大,从而引起电磁转矩和磁链脉动不断增大的弊端。 “虚拟逆变级”有效矢量的占空比减小会对转矩和磁链的波动起到强抑制作用,达到了降低转矩磁链波动、提高动态转矩的目的。其稳定性证明见附录B式(B15)—(B18)。
3 软件仿真分析
在MATLAB/Simulink 软件中搭建了图1 所示的基于MCOM 的TLDMC-PMSM-NDTC 系统,PMSM及本文所提TLDMC-PMSM-NDTC 方法的参数分别见附录C 表C1、C2。为了验证所提TLDMC-PMSMNDTC 方法的优越性,将其与常规的MC-PMSM-DTC方法在3种不同运行工况下进行仿真比较。
3.1 电机空载运行
当PMSM初始转速为600 r/min,给定的负载转矩TL=0(空载)时,2 种控制方法在不同电机电感参数下的转速n波形如图3所示(图中Ls为电机的定子电感,Lss为电机定子电感的变化值),转速控制性能如表2 所示。由图3 可知,当电机电感值发生变化时,TLDMC-PMSM-NDTC 能保持稳定运行,并且在MC-PMSM-NDTC 发生很大波动时也能保持稳定,可见所提方法提高了系统鲁棒性。由表2 可知,采用MC-PMSM-DTC 方法时转速超调量大、响应时间长,这对电机转速调整有很大影响;而采用所提TLDMCPMSM-NDTC方法时转速超调量小,响应时间短。
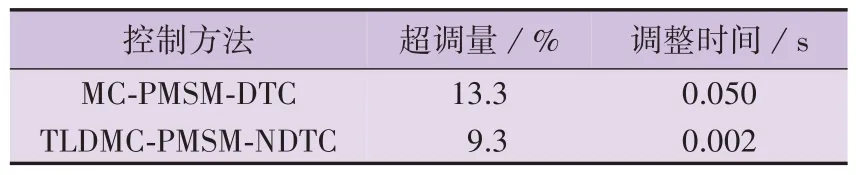
表2 空载时2种控制方法的转速控制性能Table 2 Rotational speed control performance with two control methods under no load
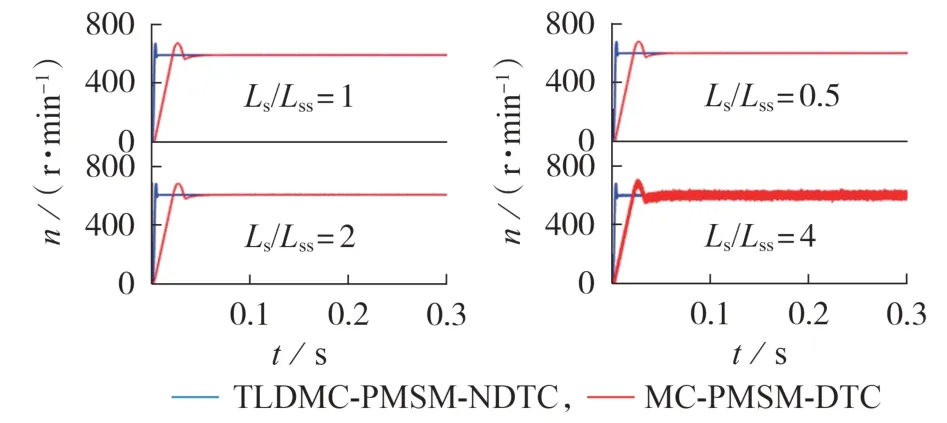
图3 空载时2种控制方法的转速波形Fig.3 Rotational speed waveforms with two control methods under no load
空载时2种控制方法的转矩波形如图4所示,转矩控制性能如表3所示。

表3 空载时2种控制方法的转矩控制性能Table 3 Torque control performance with two control methods under no load

图4 空载时2种控制方法的转矩波形Fig.4 Torque waveforms with two control methods under no load
由图4(a)和表3 可知,TLDMC-PMSM-NDTC 方法的转矩波形相比传统方法更平滑、波动小,控制效果更好。由于PMSM 控制会有低速时转矩脉动大的特点,所以抑制低速时高转矩作用时间显得非常重要,TLDMC-PMSM-NDTC 的高转矩作用时间已经缩短至0.002 s,这对电机的影响非常小,稳定后转矩脉动的大小为±0.05 N·m,可见对电磁转矩的脉动抑制效果非常好。由图4(b)可知,在TLDMC-PMSM-NDTC中,未采用MCOM 的转矩波形随后会出现波动值越来越大的现象,这样对电机的平稳运行有很大的影响,而采用MCOM 后,在误差较大时会通过减小有效矢量的占空比来减小电机转矩的脉动,这样就可以使电机一直保持在很小的波动范围内平稳运行。
3.2 电机负载转矩突变情况
当电机初始转速为600 r/min,在0.1 s 突增负载转矩TL=2 N·m(负载突变)时2种控制方法的转速波形见附录C 图C1,转速控制性能见附录C 表C3。可以看出:MC-PMSM-DTC 方法转速脉动大,且调整时间长,调整时间为0.006 s;而所提TLDMC-PMSMNDTC 的转速脉动极小,且调整时间为0.002 5 s,时间极短,控制效果好。
负载转矩突变时2 种控制方法的转矩波形见附录C 图C2,转矩控制性能见附录C 表C4。可以看出:MC-PMSM-DTC 的转矩脉动大且低速时高转矩作用时间长,这对电机运行造成了很大影响;而所提TLDMC-PMSM-NDTC 的转矩调整时间短,调整过程中转矩超调量小,且0.1 s前后的转矩脉动保持一致,可见负载转矩突变时控制效果也能保持理想状态。
3.3 电机转速突变情况
当电机转速在0.15 s 时由600 r/min 突增到800 r/min,2 种控制方法的转速波形见附录C 图C3,转速控制性能见附录C 表C5。可以看出:转速突增时,MC-PMSM-DTC 方法的转速超调量大且调整时间长,电机运行不可靠;而采用TLDMC-PMSMNDTC 方法时,可在无超调量且调整时间短的情况下快速达到设定的转速。
电机转速突变时2 种控制方法的转矩波形图见附录C 图C4,转矩控制性能见附录C 表C6。可以看出:MC-PMSM-DTC 的转矩峰值达到26 N·m,调整时间为0.025 s;而TLDMC-PMSM-NDTC 的转矩峰值仅为15 N·m,且调整时间为0.002 s,高转矩作用时间短,相比较而言,不管从高转矩作用时间、调整时间,还是从稳定时的转矩波动来看,采用所提TLDMCPMSM-NDTC对系统都有很大的提升。
当电机负载转矩在0.1 s 突增至2 N·m,转速在0.15 s 突增至800 r/min 时,2 种控制方法的磁链波形见附录C 图C5。可以看出,TLDMC-PMSM-NDTC方法的磁链是平滑的,而MC-PMSM-DTC 的磁链波动较大,电机运行不稳定,从转速、转矩突变时间点看,所提TLDMC-PMSM-NDTC 方法都能保持优良的控制效果,波形脉动小,电机运行效果好。
综上所述,PMSM 在3 种运行工况下,TLDMCPMSM-NDTC方法不论是在转速调节,还是在转矩波形调节方面都表现出良好的控制性能,转速和转矩调整时间短,脉动小且波形光滑。
4 硬件实验分析
为了进一步验证本文所提方法的优势,搭建如附录D 图D1 所示的硬件实验平台进行实验研究。该实验平台主要电路元件,如交流电源、测试和负载PMSM、TLDMC、驱动模块、测量模块等,其参数与仿真参数相同。此外,开关器件和控制芯片的型号如下:TLDMC 的双向开关采用西门康SK60GM123,其驱动模块采用6SD106EI,DSP模块采用XC3S1800A。
4.1 电机空载运行
图5 和图6 分别为空载时2 种控制方法的转速、转矩波形和A 相输出电流波形。由图可见,TLDMCPMSM-NDTC 下转速超调量小、调整时间短,转矩动态响应速度快、脉动小,且电流谐波畸变率降低,硬件实验波形与软件仿真波形相符。
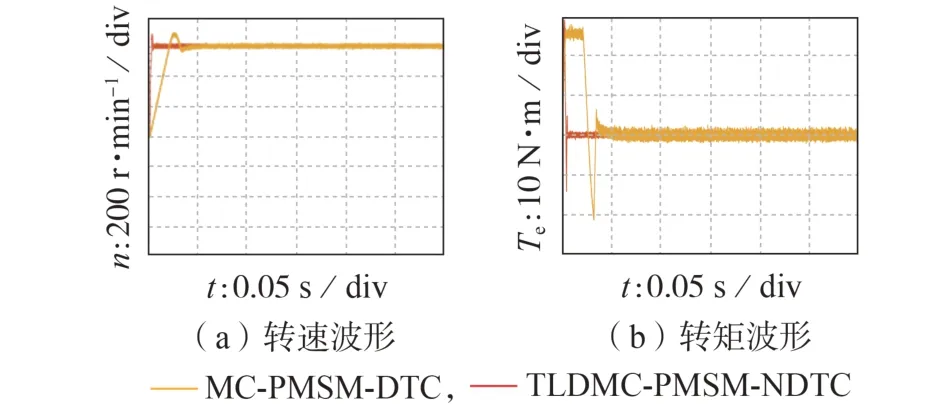
图5 空载时2种控制方法的转速和转矩波形Fig.5 Waveforms of rotational speed and torque with two control methods under no load
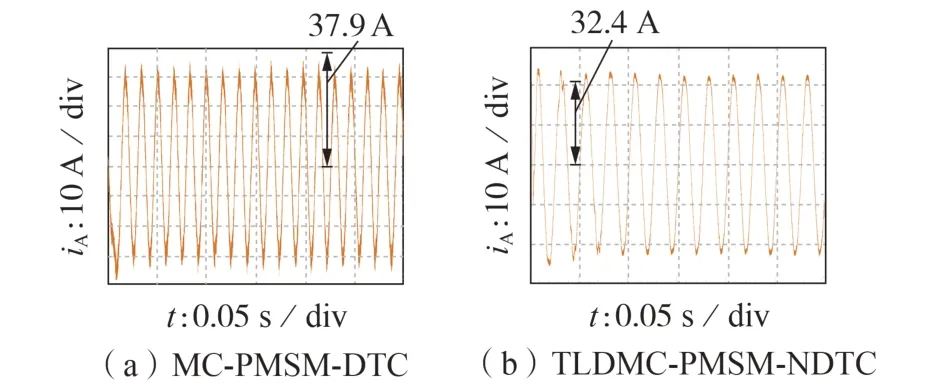
图6 A相电流波形Fig.6 Waveform of phase-A current
4.2 电机负载转矩和转速突变情况
负载转矩突变和转速突变时2 种控制方法的转速、转矩波形分别见附录D 图D2、D3 和图D4、D5。由图可见,TLDMC-PMSM-NDTC 下在负载转矩和转速突变时,转速波动小、超调量小且转矩脉动小、调节时间快,与软件仿真波形相符。
5 结论
针对传统MC-PMSM-DTC 方法会造成转速的超调量大、转矩脉动大、高转矩负载调整时间长等弊端,本文采用TLDMC-PMSM-NDTC 方法来解决。通过理论推导、仿真及实验分析可得出如下结论:
1)PMSM 采用TLDMC 进行能量传输与变换,与MC相比增加了有效矢量的个数,使得电流谐波畸变率降低,提升了系统的功率密度;
2)PMSM 转速、转矩控制采用SVPWM 和NDTC相结合的算法,不仅体现出SVPWM 控制波形平滑的优点,而且体现出DTC 对转速、转矩调节速度快的优势;
3)采用MCOM 将电机的磁链、转矩误差引入TLDMC 调制中,在误差较大时会通过减小有效矢量的占空比来减小电机磁链、转矩的脉动。
附录见本刊网络版(http://www.epae.cn)。
