分区匹配气象及功率特征的运行备用需求量化

刘 晟，向明旭，刘 硕，于松泰，杨知方

（1.重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044；2.北京电力交易中心有限公司，北京 100031）

0 引言

在电力市场环境下，运行备用的配置不仅是应对新能源等不确定性因素的主要手段，也是备用价格计算、备用成本分摊等的重要依据，其对于保障电网的安全经济运行至关重要［1-3］。运行备用的配置需综合考虑2 类主要因素，一类是发电机停运所引起的功率缺额，另一类是新能源、负荷预测随机性所引起的功率偏差。对于发电机停运的情况，现有方法主要根据单机的最大容量或发电机的强迫停运率来配置运行备用，可有效应对发电机停运的影响［4］。因此，本文主要关注新能源、负荷预测随机性对系统运行备用配置的重要影响。

现有针对新能源、负荷预测随机性的运行备用配置方法包括不确定性方法和确定性方法。不确定性方法包括多场景［5］、机会约束［6］、鲁棒优化［7］等。该类方法通过求解嵌入预测随机性的调度决策模型来实现运行备用的优化配置，不需要在求解调度决策模型前确定系统的总运行备用需求。然而，受限于计算效率、收敛性等出清计算要求，上述方法尚未在国内外的实际电力系统中得到应用。

确定性方法首先设置系统的总运行备用需求，然后通过确定性调度决策模型将总运行备用需求分配至各机组。该类方法因计算负担小而被广泛应用于工业界，其关键环节为运行备用需求量化，国内外学者对此展开了广泛的研究，主要方法包括基于运行经验的方法、基于相似日的方法、基于概率预测的方法。基于运行经验的方法根据负荷预测比例［8］、全网发电容量比例［9］等设置运行备用需求，该类方法简单、易实施，但无法考虑新能源、负荷预测随机性的影响。基于相似日的方法根据历史相似日的预测误差等数据设置运行日备用需求［10-11］，该类方法仅通过历史相似数据来考虑预测随机性的影响，未有效利用运行日的预测信息。基于概率预测的方法因能结合预测信息估计运行日的预测随机性而受到广泛关注。该类方法首先估计运行日系统整体净负荷的预测误差分布，然后以一定的置信水平来量化系统运行备用需求。根据是否在中间预测结果的基础上进行概率预测，可将概率预测方法分为间接法和直接法［12］。间接法一般先获取运行日系统整体净负荷预测功率，以此为依据进一步估计净负荷的预测误差分布［13-14］。例如，文献［13］根据预测功率将历史预测误差分成不同的区间，并分别拟合各区间的预测误差分布，最终根据运行日的预测功率选择对应区间的预测误差分布。然而，现有间接法忽略了气象因素对预测误差的重要影响，难以实现净负荷预测误差分布的准确刻画。直接法一般以气象数据、历史新能源或负荷数据等作为输入，通过数据驱动工具直接映射获得负荷或新能源的概率预测结果［15］。该类方法能够考虑气象因素以及运行日的预测信息，但一般仅关注系统负荷或单个新能源的预测误差分布，不能反映系统整体净负荷的预测随机性，难以支撑系统整体的运行备用需求量化。

综上可知，现有方法存在难以考虑气象因素对预测随机性重要影响的不足。为此，本文揭示了气象因素对系统整体预测随机性的重要影响，提出了分区匹配气象及功率特征的运行备用需求量化框架，通过将气象因素嵌入预测误差分布的刻画流程，实现系统备用需求的合理量化。为了进一步提升系统预测随机性的刻画准确性，提出了基于数据特征相似度的预测随机性精准刻画方法。该方法通过筛选与运行日特征相似的数据进行预测误差分布拟合，提升了分布刻画的准确性；通过聚合预测误差分布相似度较高的区间，实现了气象及功率的合理分区。

1 气象因素对预测随机性的影响分析

气象因素是进行新能源、负荷预测时需要考虑的重要因素，例如：风速变化会影响风电出力水平；温度变化会引起用户用电需求的变化。此外，在不同的气象条件下，新能源、负荷预测的难易程度也有所不同，例如：当温度较高时，随机性较强的空调负荷占比较高，导致负荷预测难度较大。由此可以推断，在不同的气象条件下，系统整体净负荷的预测随机性也将表现出不同的特性。为了验证这一观点，本章基于我国某省级电网的实际数据，分析气象因素（以温度为例）对系统整体预测随机性的影响。

首先，基于所收集的实际数据对系统负荷、风电场出力进行点预测［16］，从而获取净负荷预测误差数据；然后，根据温度数据的取值，将其划分为等间隔的区间，并将系统净负荷预测误差数据分配到对应的温度区间中；最后，采用非参数核密度估计方法［17］对不同温度区间内的系统净负荷预测误差分布进行拟合。非参数核密度估计f(x)的表达式为：

式中：C为某一温度区间内所有可用历史数据的数量；x为系统净负荷预测误差；xi为第i个系统净负荷预测误差数据；K（·）为核函数；h为带宽。非参数核密度估计等间隔划分了多个窗口，并对样本落入每个窗口的情况进行统计，进而整合得到样本的概率分布，其中将窗体的宽度称为带宽。非参数核密度估计方法能够从数据本身的特征出发，不需要对数据分布进行任何先验假设，适用范围广。本文采用计算相对容易且任意阶连续可导的Gaussian 核函数作为非参数核密度估计的核函数K（·），其计算公式为：

采用非参数核密度估计方法拟合得到的不同温度区间内净负荷预测误差概率分布见附录A 图A1（以2 个温度区间为例）。由图可见，不同温度区间内的系统净负荷预测随机性表现出显著差异。为了进一步说明该差异，对图A1 中区间1（［6.47，13.37］ ℃）、区间2（［13.37，16.83］ ℃）内系统净负荷预测误差的均值和标准差进行量化，得到区间1、2内系统净负荷预测误差均值分别为799、1 567 MW，标准差分别为3 888、3 695 MW。

由此可见，在不同的气象区间内，净负荷预测误差分布具有较大的差异性。因此，在刻画系统整体预测随机性、量化运行备用需求时，有必要考虑气象因素的重要影响。本文主要关注气象因素对系统预测随机性的影响，暂不考虑新能源接入规模等其他因素的影响。

2 分区匹配气象及功率特征的运行备用需求量化框架

由第1 章可知，在预留运行备用以应对系统整体预测随机性时，有必要考虑气象因素的影响。除气象因素外，现有研究表明预测功率同样对预测误差有重要的影响［18］。因此，为了综合考虑气象因素、预测功率对系统整体预测随机性的影响，本文提出了分区匹配气象及功率特征的运行备用需求量化方法，其框架如图1 所示（气象数据以温度为例）。所提方法包括分区匹配气象及功率特征的系统整体预测随机性刻画、基于系统净负荷预测误差概率分布的运行备用需求量化2个阶段。

图1 所提方法的框架Fig.1 Framework of proposed method

2.1 分区匹配气象及功率特征的系统整体预测随机性刻画

分区匹配气象及功率特征的系统整体预测随机性刻画的流程图见附录A图A2，具体步骤如下。

1）从众多历史数据集（包括各预测点的气象数据、系统净负荷预测功率数据、系统净负荷预测误差数据）中筛选出与运行日预测点相近的数据作为最终参与预测随机性刻画的数据，以实现运行日系统预测随机性的准确估计。本文所提数据筛选策略的详细介绍见3.1节。

2）根据筛选后气象数据和预测功率数据的具体数值，建立等间隔的气象-功率二维区间，并根据筛选后预测误差数据对应的气象数据和预测功率数据将其划分到不同的二维区间内。

3）采用非参数核密度估计方法分别拟合不同二维区间内系统净负荷预测误差的分布情况。

4）对预测误差分布相似度较高的区间进行聚合，使不同区间的预测误差分布表现出显著不同的特性。本文所提区间聚合策略的详细介绍见3.2节。

由此，完成了气象-功率二维区间建立，并获得了各区间对应的预测误差分布情况，可反映各区间系统整体的预测随机性，为运行备用需求量化奠定基础。

2.2 基于系统净负荷预测误差概率分布的运行备用需求量化

基于系统净负荷预测误差概率分布的运行备用需求量化流程的具体步骤如下。

首先，根据运行日各预测点对应的气象数据、预测功率数据，判断该预测点的预测误差数据所隶属的气象-功率二维区间，并将对应二维区间的预测误差分布作为该预测点的系统整体预测误差概率分布。

针对新能源、负荷预测随机性的运行备用是为了应对新能源、负荷预测误差所配置的，因此，根据系统整体预测误差概率分布便可量化系统的运行备用需求。运行备用又可分为上运行备用和下运行备用，如式（3）所示。其中：上运行备用用于应对系统计划出力不足以满足系统实际需求的情况，即净负荷实际值高于净负荷预测值，预测误差大于0（本文将预测误差定义为净负荷实际值减去净负荷预测值）的情况；下运行备用则用于应对净负荷实际值不高于净负荷预测值，预测误差不大于0的情况。

式中：R为系统的运行备用，包括上运行备用Rup、下运行备用Rdn。

通过对运行日系统整体的预测误差概率密度函数f(ε)（ε为预测误差的随机变量）进行积分，可获得其累积概率分布函数F(ε)，如式（4）所示。

根据F(ε)可获得置信水平为1-α的系统净负荷预测误差置信区间，如式（5）所示。

式中：F̂（·）为累积概率分布函数F(ε)的反函数，有pr{ε≤F̂(q)}=q，表示ε≤F̂(q)发生的概率为q，pr{·}为{ }内事件发生的概率。系统净负荷预测误差置信区间的示意图如图1的阶段2中所示。

预测误差置信区间的含义是：若系统运行备用能够覆盖该置信区间，则系统将有(1-α)×100 %的把握能够应对系统净负荷预测误差。因此，可根据净负荷预测误差置信区间以及上、下运行备用需求的配置目标量化系统运行备用需求，如式（6）所示。

式中：max 函数的目的在于应对系统净负荷预测误差分布整体大于0（即F̂(α/2)＞0）或小于0（即F̂(1-α/2)＜0）的极端情况。在极端情况下，系统不需要预留下（上）运行备用。

至此，实现了对系统运行备用需求的合理量化。如前文所述，系统整体预测随机性的准确刻画是合理量化系统运行备用需求的基础。对于本文所提基于气象-功率二维分区的系统整体预测随机性刻画方法，如何从历史数据集中筛选出参与随机性刻画的数据以及如何合理划分气象-功率二维区间是决定预测随机性刻画是否精准的关键所在。本文将在第3章对这2个核心问题进行详细探讨。

3 基于数据特征相似度的预测随机性精准刻画方法

3.1 基于气象-功率综合相似度的历史数据筛选策略

如第2 章所述，本文所提分区匹配气象及功率特征的运行备用需求量化方法是通过拟合历史预测误差数据的分布来估计运行日的预测误差分布。在众多的历史数据中，预测误差分布特性与对应预测点的气象数据、预测功率密切相关。为了准确估计运行日的预测误差分布，本文提出了基于气象-功率综合相似度的历史数据筛选策略。相比于直接选用所有历史数据，通过所提数据筛选策略可挑选出与运行日特征最相似的数据来估计运行日的预测误差分布，从而避免特征关联性较低的数据影响预测误差分布估计的准确性。所提数据筛选策略的思路与负荷预测中的相似日选取方法类似，区别在于相似日选取一般针对运行日所有预测点的综合特征相似程度，而对于本文所提数据筛选策略而言，鉴于同一运行日的不同预测点具有不同的气象和预测功率特征，本文分别针对运行日的每一个预测点进行数据筛选和预测误差分布拟合，关注单一预测点的特征相似度。本文所提数据筛选策略的思路具体如下。

距离度量是衡量数据特征相似度的有效手段。鉴于气象数据和预测功率是影响预测误差分布特性的重要因素，本文通过计算运行日预测点与历史气象-功率数据的加权综合距离d来评估历史数据与运行日预测点数据的特征相似度，如式（7）所示。

式中：dm、dp分别为运行日预测点与历史数据点之间的气象距离、预测功率距离；wm、wp分别为气象距离、预测功率距离的权重系数。

本文采用目前应用广泛的欧氏距离计算运行日预测点与历史数据点之间的气象距离和预测功率距离，欧氏距离的计算公式为：

式中：dE为计算的欧氏距离；a=[a1，a2，…，aD]、b=[b1，b2，…，bD]为2个D维数据向量。

可通过分别分析历史数据集中气象数据、预测功率与预测误差的相关性得到式（7）中气象距离、预测功率距离的权重系数。Spearman相关性系数可用于计算不满足正态分布的数据之间的相关性，经数据正态分布检验，本文使用的历史数据均为非正态分布，故本文采用Spearman 相关性系数进行相关性分析，其计算公式为：

式中：rs为数据集x与数据集y之间相关性的Spearman 相关系数；xi、yi分别为数据集x、y中的第i个数据；n为数据集中的数据数量；Rxi、Ryi分别为数据集x、y中数据从小到大排序后数据xi、yi对应的次序。

基于式（7）所得加权综合距离d可衡量运行日预测点与历史数据点之间的相似程度，然后，可筛选出特征相似度最高的前M个数据作为最终参与运行日预测误差分布估计的数据集。

3.2 基于预测误差分布相似度的数据区间划分策略

预测误差的分布特性与对应预测点的气象和预测功率密切相关，考虑到这一特性，本文第2 章划分了气象-功率二维区间，以区分不同气象、预测功率条件下的预测误差分布特性。在理想的区间划分下，不同区间内的预测误差分布应各不相同。为此，本文提出了基于预测误差分布相似度的数据区间划分策略。

首先，将筛选后的气象数据和预测功率数据分别按数值大小进行等间隔划分，如式（10）所示。

式中：nr为气象数据或预测功率数据的分区数量；xmax、xmin分别为筛选后气象数据或预测功率数据的最大值、最小值；Δx为等间隔区间的宽度。则每一个气象区间或预测功率区间的上下限范围为[xmin+(ir-1)Δx，xmin+irΔx] ，其 中ir为 区 间 编 号，ir=1，2，…，nr。

分别对气象数据和预测功率数据进行等间隔划分后，便可建立气象-功率二维区间，如附录A 图A2所示。但等间隔划分难以保证每个二维区间内数据量的充足性，不充足的历史数据难以反映不同区间内预测误差的实际分布特性。为此，将数据量不充足的二维区间与相邻的区间进行合并，以保证每个二维区间内数据量的充足性。

至此，实现了气象-功率二维区间的初步建立，通过非参数核密度估计方法可拟合得到不同区间内预测误差的分布情况。如前文所述，在理想的情况下，不同区间内的预测误差分布应各不相同。显然，通过等间隔初步划分的区间难以实现上述目标，个别区间内的预测误差分布情况可能相似。为了改善这一问题，本文提出利用JS（Jensen-Shannon）散度刻画不同区间内预测误差分布的差异性，并将分布相似的区间进行聚合，以保证不同区间之间预测误差分布的差异性。

首先，利用JS 散度计算不同二维区间之间预测误差分布的差异性，如式（11）所示。

式中：P、Q为待比较相似度的2 个概率分布函数；γJS(P‖Q)为JS 散度。JS 散度的取值范围为0～1，其值越小，则概率分布函数之间的相似度越高。

JS 散度存在难以有效表征分布之间距离的问题，为此，本文通过比较2 个不同分布之间0.001 %分位数和99.999 % 分位数的相对差异来表征分布之间的距离。最终，通过比较JS 散度阈值J以及分位数相对差异阈值Δd来判断不同区间的预测误差分布是否相似（只有当0.001 % 分位数和99.999 % 分位数的相对差异均小于阈值Δd时，才认为2 个分布相似）。对于预测误差分布相似的区间，本文对其进行聚合，并采用聚合区间内的所有数据点重新拟合预测误差分布，将其作为该聚合区间的预测误差分布。该区间聚合策略可保证不同区间之间预测误差分布的差异性。

至此，实现了气象-功率二维区间的建立，并获得了各二维区间内的预测误差分布，可为运行备用需求的合理量化奠定基础。

4 算例分析

4.1 算例说明

本文以我国某省级电网的实际661 节点系统（包含2 座风电场）为算例进行仿真分析，以验证所提方法的有效性。仿真所用负荷、新能源数据同样源自该省级电网。其中，以2017年1月16日至2017年6 月15 日的数据作为可用历史数据，2017 年6 月16 — 29日的数据作为运行日测试数据。

为了验证本文所提系统整体预测随机性刻画方法的有效性，对以下5 种方法进行对比分析：①方法1，本文所提分区匹配气象及功率特征的系统预测随机性刻画方法（置信水平为90 %，筛选的历史数据数量M=8 640；数据区间聚合策略中，JS 散度阈值J=0.1，分位数相对差异阈值Δd=8 %）；②方法2，同方法1，但不采用历史数据筛选策略，而是采用运行日前90 d的数据（共计8 640个数据）；③方法3，同方法2，但采用所有历史可用数据（共计14 400 个数据）；④方法4，同方法1，但仅考虑预测功率一维分区，不考虑气象因素［13］；⑤方法5，同方法1，但不采用数据区间聚合策略。

为了比较不同方法对预测随机性的刻画效果，本文采用预测区间覆盖率（prediction interval coverage probability，PICP）、预测区间宽度（prediction interval width，PIW）、Winkler 分数［12］作为评价指标，具体计算公式见附录B。

为了验证本文所提运行备用需求量化方法的有效性，设置如下对比方法：①方法a，基于运行日预测误差分布估计的运行备用需求量化方法，采用上述方法1 刻画运行日系统整体的预测随机性，置信水平为90 %；②方法b，同方法a，但采用上述方法4 刻画运行日系统整体的预测随机性；③方法c，同方法a，但分别对负荷、新能源的预测随机性进行估计，并分别获得针对负荷、新能源的运行备用需求，通过将所有运行备用需求直接相加作为系统的总运行备用需求；④方法d，将运行备用需求设置为净负荷功率预测值的10 %［8］；⑤方法e，将运行备用需求设置为净负荷功率预测值的20 %［8］。

本文所用计算机硬件环境为AMD Ryzen 75800 H，Radeon Graphics 3.20 GHz，16.0 GB RAM。

4.2 仿真结果分析

4.2.1 预测随机性刻画方法对比

1）不同气象因素下各方法的效果对比。

负荷、风电预测需考虑的气象因素主要包括温度、湿度、风速等。在不同的气象因素下，采用方法1对系统整体预测随机性进行刻画，总体刻画效果如表1 所示。表中：平均PICP、平均PIW、平均Winkler分数均为14 d 运行日测试数据的平均指标；最低PICP为测试日所有预测点的最低PICP。

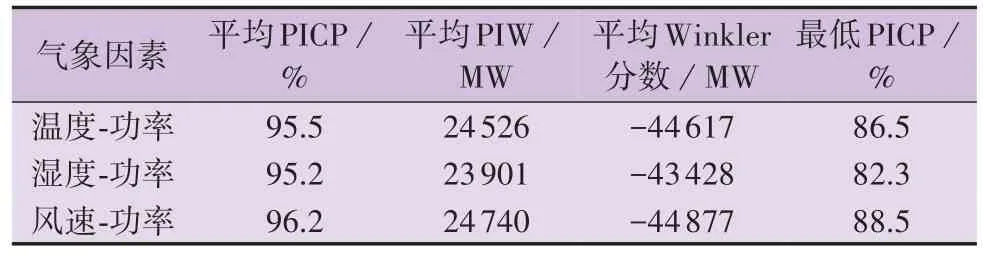
表1 不同气象因素下方法1的总体刻画效果Table 1 Overall characterization effect of Method 1 under different meteorological factors

由表1 可知，在3 种气象因素下，方法1 的平均PICP 均可满足所设置的置信水平。其中，考虑湿度因素时，平均PIW 最小，这有助于提升系统的运行经济性，且此时的平均Winkler 分数绝对值也较小，表现出了较好的平均综合性能，但最低PICP 相对较小，为82.3 %，可见湿度因素在保障系统运行安全性方面不如其他2 种气象因素。相较而言，当考虑风速因素时，平均PICP 较高，平均PIW 也较大，导致平均Winkler 分数指标相对较差。而当考虑温度因素时，预测随机性的刻画效果介于考虑湿度、风速因素的效果之间，其平均PICP 相比考虑湿度因素时高，平均PIW 比考虑风速因素时小，平均Winkler分数也介于考虑湿度、风速因素的平均Winkler 分数之间。为了使系统运行备用需求的量化能够兼顾系统的运行安全性与经济性，本文后续选用温度代表气象因素（即建立温度-功率二维区间以刻画系统整体的预测随机性）。

2）不同预测随机性刻画方法的效果对比。

不同预测随机性刻画方法对所有运行日系统预测随机性的总体刻画效果见表2。

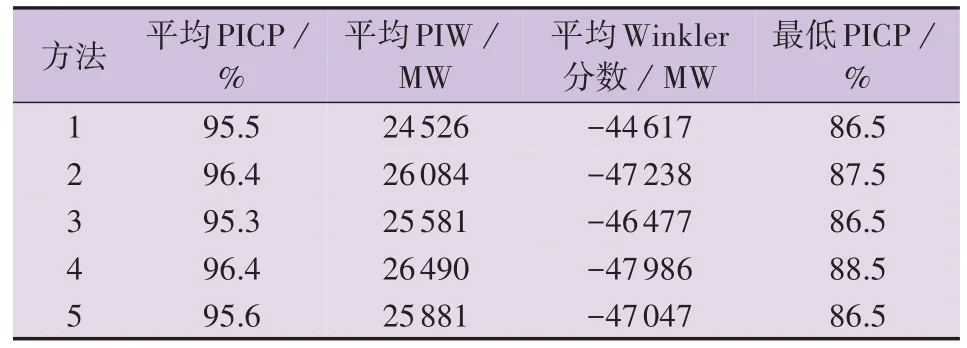
表2 不同预测随机性刻画方法的效果对比Table 2 Comparison of effect among different forecasting uncertainty characterization methods

由表2可知：方法1 — 3的平均PICP均可满足所设置的置信水平（90 %），且所有运行日的最低PICP也均高于85 %，与置信水平相近，表明这3 种方法均能保障系统的运行安全性；然而，相较于方法2 和方法3，方法1 的平均PIW 分别减少了5.97 %、4.12 %，方法1 据此量化的运行备用需求将会表现出更优的经济性；方法1 的平均Winkler 分数绝对值最小，表明方法1 的综合性能比方法2 和方法3 更优。上述结果验证了本文所提基于气象-功率综合相似度的历史数据筛选策略的有效性，表明参与预测随机性刻画的历史数据并非越多越好（体现在方法1 的刻画效果优于方法3）。

对比表2 中方法1 和方法4 的结果可以发现，在平均PICP 和最低PICP 均能满足系统运行安全性要求（PICP 满足或接近置信水平）的条件下，方法1 的平均PIW比方法4减少了7.41 %，据此量化的运行备用需求可显著提升系统的运行经济性。对比平均Winkler 分数可以发现，方法1 的综合性能优于未考虑气象因素的方法4。由此，验证了计及气象因素的必要性。

对比表2 中方法1 和方法5 的结果可以发现，在平均PICP 和最低PICP 相差无几且均能满足系统运行安全性要求的条件下，方法1 具有更小的平均PIW 和平均Winkler 分数绝对值，这表明基于方法1量化的运行备用需求将具备更优的系统运行经济性和综合运行性能。由此，验证了本文所提基于预测误差分布相似度的数据区间划分策略的有效性。

综上可知，相比于其他预测随机性刻画方法，本文所提方法在平均PICP 满足系统运行安全性要求的前提下，能够有效减少平均PIW，据此量化的运行备用需求将更能保障系统的运行经济性。

4.2.2 运行备用需求量化方法对比

本节采用我国某省级电网的实际661 节点系统进行仿真分析，以阐述本文所提运行备用需求量化方法（方法a）的有效性。

1）不同运行备用需求量化方法的效果对比。

所有运行测试日的系统平均备用覆盖率（即所预留的上、下运行备用能够覆盖系统净负荷预测误差的比例）、最低备用覆盖率、平均备用成本和出清模型的平均计算时间（出清模型采用文献［3］中所提调度决策模型）结果如表3 所示。由表可知，基于预测误差分布的方法（方法a — c）的平均备用覆盖率均可满足所设置的置信水平（90 %），且最低备用覆盖率也均超过85 %，这表明方法a — c均能够保证系统运行备用的充裕性。然而，相较于方法b、方法c，方法a的平均备用成本最少，方法a表现出更优的系统运行经济性。对比方法a 和方法c 的结果可以发现，方法c 通过叠加针对不同负荷、新能源的运行备用需求，所获得的系统总运行备用需求难以有效反映系统整体的预测随机性，所得运行备用需求量化结果偏保守（所有运行日中的最低备用覆盖率也达到91.7 %），会引起不必要的经济损失。

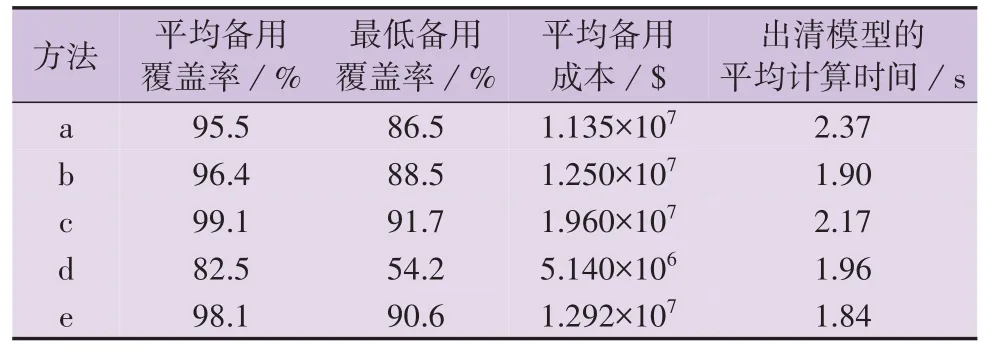
表3 不同运行备用需求量化方法的性能对比Table 3 Comparison of performance among different operating reserve demand quantification methods

目前，工业界所用方法——方法d和方法e的性能依赖于运行经验（即运行备用需求占净负荷预测值比例的设置）：当比例设置较小（如方法d）时，系统运行备用的充裕性难以保障；当比例设置较大（如方法e）时，能够满足系统运行备用充裕性要求，但过大的比例同样会引起不必要的经济损失（具体表现在方法e 的平均备用成本高于方法a 和方法b）。但是，目前仍缺乏合理设置该比例的理论依据。

对比表3 中平均备用覆盖率能够满足系统运行备用充裕性的方法（方法a — c、e）可以发现，方法a的平均备用成本最少，这验证了本文所提运行备用需求量化方法的有效性。此外，在计算时间方面，方法a — e均采用确定性调度决策模型，在大规模实际系统中的计算效率均能满足计算需求。

2）本文所提方法在运行日不同调度时段的性能分析。

为了进一步验证本文所提方法的有效性，以2017 年6 月16 日为例，当采用方法a 和方法b 时，同一运行日不同调度时段的运行备用充裕度如图2 所示，图中运行备用为正值时表示上运行备用，为负值时表示下运行备用。由图可知，方法b 在11 个调度时段内无法有效覆盖系统净负荷预测误差，而本文所提方法（方法a）仅在6 个调度时段内无法覆盖预测误差。此外，方法a、b在该运行日所有调度时段的运行备用预留总量分别为2.33×106、2.51×106MW。由此可见，方法a 可以通过更少的运行备用满足更多调度时段的运行备用需求，验证了本文所提方法的有效性。

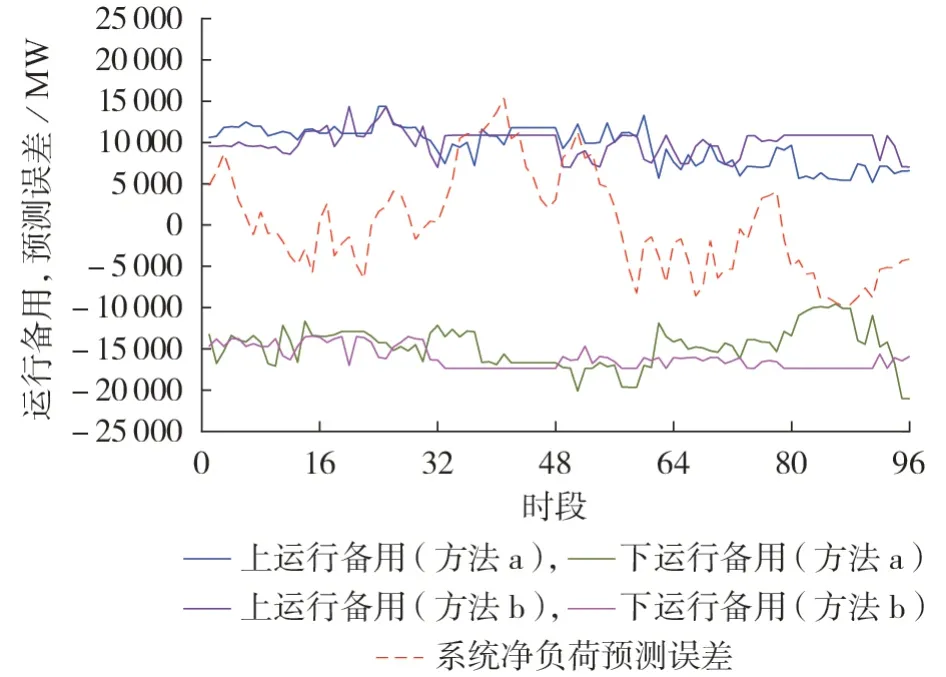
图2 不同方法的运行备用充裕度对比Fig.2 Comparison of operating reserve adequacy between different methods

3）本文所提方法在不同置信水平下的性能对比。

以2017 年6 月16 日这一运行日为例，本文所提方法（方法a）在不同置信水平下的运行性能见表4。由表可知，随着置信水平的增大，备用覆盖率增大，系统运行备用充裕性有所提高，但备用成本也随之增大，系统运行经济性有所下降。因此，通过调整置信水平，本文所提方法可在运行备用充裕性和运行经济性之间进行权衡。

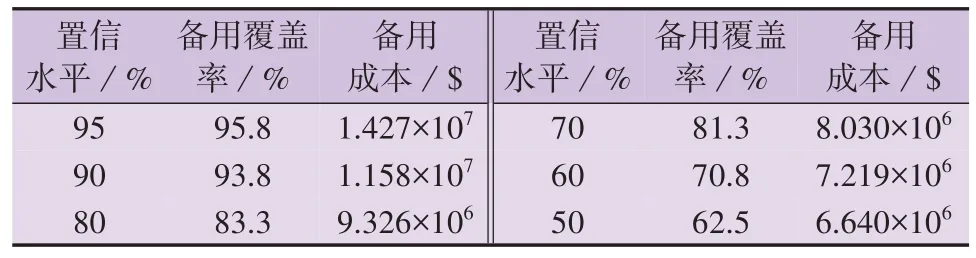
表4 不同置信水平下所提方法的性能对比Table 4 Comparison of performance of proposed method under different confidence levels

5 结论

针对现有运行备用需求量化方法难以有效考虑气象因素对系统预测随机性重要影响的问题，本文提出了分区匹配气象及功率特征的运行备用需求量化方法。该方法根据历史数据筛选策略及数据区间划分策略，将历史预测误差数据划分至不同的气象-功率二维区间，通过拟合、匹配不同区间内的历史预测误差分布来精准刻画运行日的预测随机性，据此实现系统运行备用需求的合理量化。基于我国某省级电网实际数据的算例仿真结果表明，本文所提预测随机性刻画方法能够准确估计运行日净负荷的预测误差分布，据此量化的运行备用需求能够兼顾运行备用充裕性和系统运行经济性。此外，通过调整置信水平，所提方法可在运行备用充裕性和系统运行经济性之间进行权衡。

综上，本文计及气象因素对系统整体预测随机性的影响，实现了运行备用需求的合理量化。针对电力市场环境，未来将进一步研究运行备用成本的市场化分摊方法，以保障备用资源市场的收益，促使新能源等市场主体降低自身的预测随机性。此外，本文仅考虑了单一气象因素对系统整体预测随机性的影响，实际上所提方法也可考虑多维气象因素的综合影响，但这需要将有限的样本点划分至更加精细的多维区间中，如何确保多维区间内预测随机性的刻画精度仍有待进一步研究。

附录见本刊网络版（http：//www.epae.cn）。