计及风机运行状态差异的风电场频率协同支撑控制

2024-03-26冀肖彤江克证姚雅涵文劲宇

电力自动化设备 2024年3期

冀肖彤，江克证，姚雅涵，柳丹，姚伟，曹侃，文劲宇

（1.华中科技大学电气与电子工程学院强电磁技术全国重点实验室，湖北武汉 430074；2.国网湖北省电力有限公司，湖北武汉 430077；3.国网湖北省电力有限公司电力科学研究院，湖北武汉 430077）

0 引言

近年来，风电渗透率不断上升，但风机（wind turbine，WT）通过电力电子设备并网，其转速与系统频率解耦，无法直接对电网提供频率支撑［1-2］。大规模风电并网将减小系统的频率响应容量，降低系统惯量［3］。因此，许多国家对风电场提供主动频率支撑提出了要求。例如，我国的《风电场接入电网技术规定》中提到：风电场应具备参与电力系统调频的能力［4-5］。因此，国内外学者针对风电场的频率控制进行了相关的研究，以提升系统频率稳定性。

风电场内的风机可通过减载控制［6-8］和转子动能控制2 种方式参与调频［9］。但采用减载控制方式会造成弃风，降低风电场的运行经济性。然而，转子动能控制可以在风机正常工作于最大功率点跟踪（maximum power point tracking，MPPT）模式的基础上实现，通过释放转子动能对系统提供频率支撑，相比于减载控制更经济。为了实现转子动能控制，一般采用附加控制（如下垂控制和虚拟惯量）与MPPT控制叠加的方式［10］。在风机提供频率支撑的过程中，由于风机需释放／储存转子动能，其转速将根据调频方向下降／上升。一方面，风机转速具有安全范围，若转速超限，则可能引起风电场退网等严重事故。另一方面，风电场内存在尾流效应，即场内各风机的风速不均，转速存在差异，可提供的频率支撑能力也各不相同［11］。基于以上原因，在设计风电场的频率控制策略时，需综合考虑场内不同风机的运行状态差异，协同各风机进行调频，这样才可最大限度地利用风电场的调频能力，提升系统的频率表现。

为了解决尾流效应所带来的问题：文献［12］提出了针对不同风机的调频能力量化的评估方法，并在此基础上根据各风机的调频能力对不同风机采用自适应的频率控制，但只考虑了风机间运行状态的差异，未对各风机进行协同控制，从而无法最大化利用风电场的调频能力；文献［13］针对风电场和风机2个层面提出了一种集中式控制（centralized control，CC）策略，将风电场看作整体进行调频控制，然而CC存在通信可靠性低且通信延时影响较大的固有问题；为了解决上述控制问题，文献［14］提出了一种一致性分布式控制策略，风机通过跟随主导风机的工作状态参与调频，虽然该策略可以有效地实现风机按调频能力出力，但其采用有领导式算法，控制效果易受主导风机的影响，主导风机发生通信故障会造成整座风电场无法参与调频。

除了尾流效应带来的风机协同问题外，由于风机具有转速限制，风机在经过频率支撑阶段的转速变化后，需要对其转速进行恢复，即进入转速恢复阶段。然而由于风机回到原运行点需要减少出力，系统将会出现功率缺额，若对风机的转速恢复控制策略设计不当，则可能会造成系统频率回升后的二次频率跌落问题。当二次频率跌落现象严重时，二次频率最低点甚至将超过一次频率最低点。针对系统的二次频率跌落问题，文献［15］将风电场内的风机按风速大小分为2个集群，由风速较高的集群1首先进行频率支撑，在集群1 进入转速恢复阶段时，集群2启动增加出力，从而弥补集群1进入转速恢复阶段造成的功率缺额。然而，所提出的时序控制较复杂，且可能造成三次频率跌落问题。文献［16］针对风机提出了一种两阶段的变比例系数控制器来缓解二次频率跌落问题，然而该控制策略的控制效果严重依赖于模糊控制器的提前训练效果，在不同的情境下都需要重新训练，因此控制不具有普适性。

综上，针对风电场尾流效应带来的风速分布不均问题，本文提出了一种计及风机运行状态差异的风电场频率协同支撑控制策略。在频率支撑阶段，风机间通过一致性算法实现风电场出力的合理分配，并在此基础上采用自适应算法进一步保障风机的安全运行。针对风机进入转速恢复阶段后的二次频率跌落问题，本文采用一种渐进转速恢复策略，实现频率支撑阶段到转速恢复阶段的平滑切换，从而缓解二次频率跌落问题。

1 无领导自适应的风电场分布式控制架构

由于风机具有主动快速调频的潜力，风电场在系统发生频率事件后，将进入频率支撑阶段参与调频。然而，由于尾流效应的存在，各风机所处风速不同，相应的调频能力也不同，因此需要在风机之间按能分配风电场的频率支撑功率，协同风机来最大化利用风电场的频率支撑能力。为了实现上述目标，本文采用了一种自适应分布式控制，风机之间通过一致性算法交换状态信息，实现场内所有风机的状态跟随，并通过各风机调频系数的自适应调整进一步保障风机安全运行。在频率支撑过程中，由于风机采用转子动能控制，其转速将发生变化，然而风机具有转速安全范围。因此，所提控制在使风机提供一定时间的频率支撑后，将对其进行转速恢复。为了缓解转速恢复阶段出现的功率缺额造成的二次频率跌落问题，本文采用渐进转速恢复控制策略。

本文所提风电场参与调频的协同控制框架如图1 所示，包含频率支撑阶段和转速恢复阶段两部分。图中：Pref，i为WTi的定子功率参考值；WT1— WTN为风电场中的风机，N为风电场中风机的数量；ωr，i为WTi的实时转速；fMPPT(ωr，i)为WTi实时转速对应的捕捉MPPT 功率；ΔPw，i为综合惯量控制的附加功率。当发生频率突变事件后，各风机控制器接收到频率偏差超过阈值的信号S，风电场将进入频率支撑阶段。各风机采用综合惯量控制，根据系统测量频率与参考频率fref的偏差Δf以及频率变化率df/ dt，通过释放转子动能提供频率支撑。风机的调频系数包括下垂系数kdr，i和惯性系数kin，i（其取值均小于0），其将随着风机转速实时变化，避免风机过度出力造成转速失稳。同时，风机将与邻近风机交换一致性因子Ci，计算出状态功率修正量ΔPci，以修正自身的功率参考值。当风机进入频率支撑阶段固定时间（该时间可根据风机惯量、风电场容量、系统规模等设置）后，风机控制器接收到控制转换信号S，风机采用渐进恢复策略从频率支撑阶段平滑切换到转速恢复阶段，以避免二次频率跌落。随着转速恢复系数kr(t)的变化，渐进恢复曲线在预设转速恢复时间后与MPPT 曲线重合，风机工作点将顺延着MPPT 曲线回到原工作点。综上可知，本文所提无领导自适应的风电场分布式控制主要包含2个阶段：阶段1为风电场的自适应分布式协同频率支撑控制；阶段2为风机的渐进转速恢复控制。

图1 风电场参与调频的协同控制框架Fig.1 Collaborative control framework for wind farm participation in frequency regulation

2 无领导自适应的风电场分布式控制原理

2.1 阶段1：风电场的自适应分布式协同频率支撑控制

受尾流效应的影响，同一风电场内风机的工作状态各异。若忽略该差异，将风电场视为整体，对各风机采用统一的控制方式，则会造成风电场所分配的频率支撑功率过大，支撑能力弱的风机转速失稳，提前退出调频的情况，或者风电场所分配的频率支撑功率较小，风电场能力利用不充分的问题。

为了更合理地对不同风机分配频率支撑功率，并使风机协同参与调频，本文控制采用一致性算法。一致性算法广泛应用于微电网，用来解决分布式电源的协同控制问题，该算法包括有领导型、无领导型2 种［17］。当使用有领导型一致性算法时，至少存在1 个智能体作为领导者，用于接收参考指令，其他个体跟随该领导者的状态进行动作；当采用无领导型一致性算法时，各智能体的地位相同，并根据邻近智能体更新自身状态，从而实现全局状态相近的控制目标。由于有领导型一致性算法依赖于主导风机的通信状态，其可靠性相比于无领导型一致性算法较低，因此本文控制采用无领导型一致性算法。采用一致性算法需对风机提出一个状态指标，用于衡量各风机的当前可用出力能力。风机的出力方程为：

式中：Pm为风机的输入机械功率；Pe为风机输出的电磁功率；ωr为风机转速；Hw为风机的转动惯量。对式（1）两边积分可得：

式中：ωr，i0为WTi的初始转速；t0为积分初始时刻（频率支撑阶段开始时刻）。而风机的转子动能Ek可表示为：

综上可知，风机提供频率支撑实际上是释放转子动能来换取电磁能。因此，风机的频率支撑能力可用介于风机初始转速与转速限值范围内所对应的动能（一般为0.7～1.2 p.u.［15］）表示。而各风机在调频开始前的转速不一致，但其状态指标在调频初始时需要保持一致，基于上述讨论，本文提出了式（4）所示状态指标，即一致性因子Ci。

式中：ωr，lim为风机转速的最高／最低限值，对应向下／向上调频场景。该状态指标具有明确的物理意义，表示该风机实时可用调频能力相较于初始调频能力的偏移。

为了实现风机在调频过程中状态一致变化，使风机与邻近风机交换一致性因子，并采用一致性算法，通过计算与邻近风机的一致性因子偏差，对风机的功率参考值进行修正，功率修正值为ΔPci，也称其为状态功率修正量，可表示为：

式中：kP，i、kI，i分别为WTi与邻近风机之间状态偏移的比例、积分系数；nij为WTi与WTj之间的通信系数，若风机之间有通信链路则nij= 1，否则nij= 0。以N=5为例，5 台风机之间的通信链路如图2 所示。

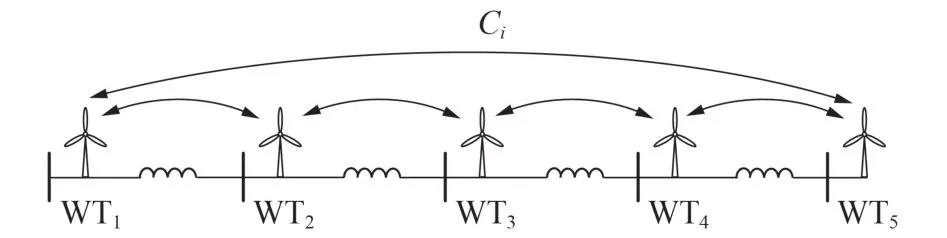
图2 风机之间的通信链路示意图Fig.2 Schematic diagram of communication link among WTs

考虑到风电场整体的经济性，本文对风机采用基于转子动能控制的综合惯量控制，综合惯量控制的附加功率ΔPw，i可表示为：

为了进一步预防各风机出力过大导致的转速过低现象，在调频过程中需对调频系数kdr，i、kin，i进行自适应调整。而式（4）所示一致性因子Ci会随着风机开始参与调频逐渐减小，表明风机的可用动能逐渐减小，且所有风机的一致性因子Ci初始值均为0。因此将1-Ci作为新系数，使各调频系数随着1-Ci的变化而变化。综上可得调频系数kdr，i、kin，i分别为：

式中：ksdr、ksin分别为下垂系数、惯性系数的固定部分；kcdr0、kcin0分别为下垂系数、惯性系数的自适应部分。

综合考虑一致性算法得到的状态功率修正量ΔPci可得到附加功率值ΔPi的具体表示式如式（9）所示。各风机采用附加控制，输出的定子功率参考值在MPPT 控制上叠加附加功率值，其整体控制框架如式（10）和式（11）所示。

式中：kMPPT为MPPT曲线的最优跟踪系数。

2.2 阶段2：风机的渐进转速恢复控制策略

风机通过快速释放转子动能提供频率支撑，然而其存在安全转速范围，无法作为持续能量源，因此在风机提供了一段时间的频率支撑之后，需要对其进行转速恢复，此时由系统中的传统同步机继续提供频率支撑。根据式（1）所示风机的转子动能方程，风机转速恢复需要降低输出的电磁功率，若采用不合适的转速恢复控制，则造成的功率缺额可能引起系统二次频率跌落。

为了最大限度地利用叶片捕捉动能，风机在参与调频前采用MPPT 工作模式，其原工作点处于输入机械功率与MPPT 曲线的交点处，MPPT 曲线的表达式如式（11）所示［18］。为了实现风机频率支撑阶段到转速恢复阶段的平滑切换，风机在频率支撑阶段出力的末值应该与转速恢复阶段的初值一致，又考虑到风机工作点将回到MPPT 曲线，设置风机在转速恢复阶段的出力沿着调整系数后的MPPT 曲线，即一种渐进恢复曲线，如式（12）所示。

式中：t1=t0+Δtf，Δtf为设定的频率支撑时间。若Δtf太长，则可能导致风电场内风机过度参与调频使转速降低／升高至安全转速范围外；若Δtf太短，则风机无法有效提供频率支撑以及提升频率最低点。因此设定的频率支撑时间Δtf须综合考虑风机转动惯量、系统等效惯量、阻尼等参数进行选择。转速恢复系数kr(t)的初值需满足转速恢复阶段风机的初始出力与频率支撑阶段的末值出力相等，且其取值随时间线性变化，在设定的转速恢复时间Δtr后取值变为1。转速恢复系数kr(t)的表达式为：

转速恢复阶段可实现风机从频率支撑阶段到转速恢复阶段的平滑切换，并能使风机工作点在设定的转速恢复时间后恢复到MPPT 曲线上，避免恢复时间过长，影响风机为下一次的频率事件做准备。最后，风机将沿着MPPT 曲线恢复到事故发生前的初始工作点。

综上，风电场参与调频的整体流程如下：①当检测到系统频率偏差的绝对值大于0.02 Hz 时，WTi的控制器测得其初始转速，开始参与调频；②WTi根据式（4）实时计算其一致性因子Ci，并与邻近风机交换各自的状态指标，控制器计算状态功率修正量ΔPci，不断修正其功率参考值，同时调频系数根据式（7）和式（8）自适应变化，预防风机转速达到安全限值；③经设定的频率支撑时间Δtf后，按照式（13）计算转速恢复系数kr(t)，风机按渐进恢复曲线进行转速恢复，经设定的转速恢复时间Δtr后，风机工作点回到MPPT 曲线上；④风机沿MPPT 曲线回到初始工作点，转速回到初始值ωr，i0。

3 算例分析

3.1 含风电场的4机2区系统

基于MATLAB／Simulink 平台搭建的含风电场的4 机2 区系统模型如附录A 图A1 所示，其中风电场内共有5台聚合风机（WT1— WT5），每台聚合风机表示50 台容量为2 MW 的双馈风机［19］，风机的转动惯量均为4 s，均采用文献［20］中的3阶模型表示（包含原动机、发电机、背靠背变流器等）。初始时风机稳定运行在MPPT 模式下。该系统的基准容量为100 MV·A，额定频率为50 Hz。稳定运行状态下，同步机G1— G4的出力分别为189、700、800、650 MW，风电场的出力为447 MW，同步机G1、G2的时间惯量为10 s，同步机G3、G4的时间惯量为12.35 s。

3.1.1 负荷突增场景

设场景1 为母线7 在t=5 s 时发生800 MW 的负荷突增事件。该场景下，采用本文所提计及风机运行状态差异的风电场频率协同支撑控制策略（本文策略）、CC 策略、无风电参与调频（no wind turbine participating，NoWT）策略时，系统频率、风电场出力结果如图3 所示，图中风电场出力为标幺值，后同。不同控制策略下各风机的转速见图4，图中ωr为标幺值，后同。当采用CC策略时，各风机采用与本文策略相同的自适应调频系数，且各风机的初始调频系数相同，但风电场内风机之间不进行信息交换。如图1中控制框架所示，采用CC策略时，各风机提供频率支撑时的出力参考值不包含状态功率修正量ΔPci；且在转速恢复阶段，CC 策略采用阶跃式转速恢复策略，在短时间内将风机的附加功率值ΔPi减为0，使风机转速快速回到负荷突增事件发生前的初始值。

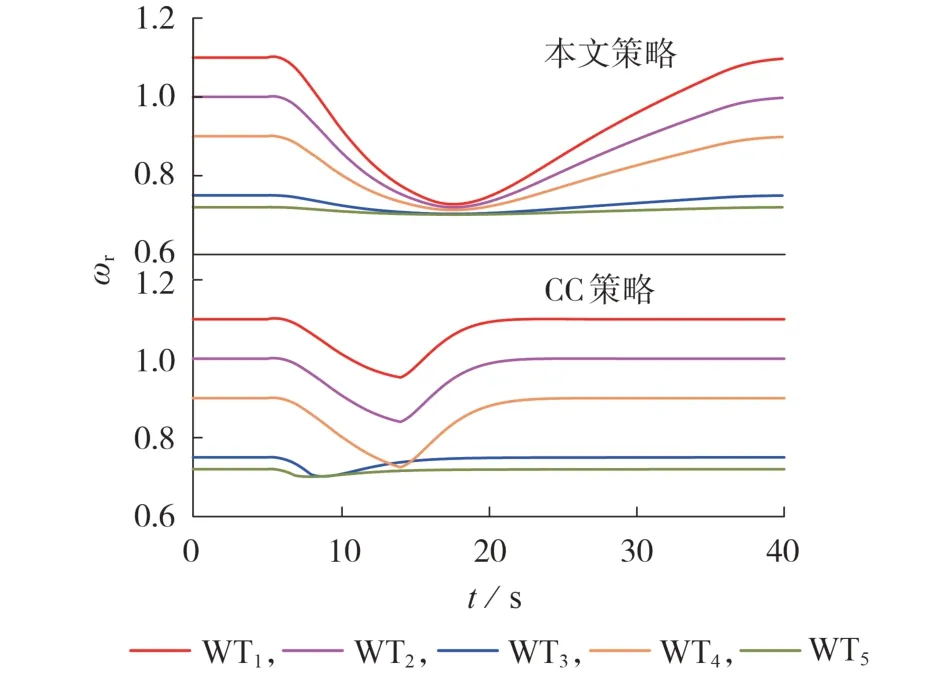
图4 不同控制策略下的风机转速Fig.4 Rotor speed of WTs under different control strategies

由图3 可知：相比CC 策略，本文策略可有效将频率最低点由48.73 Hz 提升至48.81 Hz，而相比NoWT 策略，本文策略可将频率最低点提升0.21 Hz；采用CC 策略时，在频率支撑控制后的10～14 s 时段内风电场出力下降，且在14.5 s 时产生较大的功率缺额，风电场2 次较大的出力变化导致CC 策略的频率表现比本文策略差。由图4 可知，当采用本文策略时，各风机在一致性算法的引导下按能出力，在整个调频过程中风电场内无风机转速达到最低限值。本文策略在转速恢复阶段采用渐进转速恢复控制策略，各风机可平滑地实现转速恢复，且当风机从频率支撑阶段切换至转速恢复阶段时，风电场出力没有明显的功率缺口出现。而当采用CC策略时，由于各风机采用统一控制方式，而WT3、WT5的初始转速较低，在调频过程中没有与邻近风机交换状态信息的过程，因此即使各风机都采用自适应调频系数，WT3、WT5的转速仍在频率支撑阶段结束前达到最低限值，提前触发了转速保护控制，使其快速退出调频，导致CC策略下风电场频率支撑后半段的出力相比本文策略减少的现象。在14.5 s 频率支撑阶段结束时，由于CC策略采用了阶跃式转速恢复控制策略，未退出调频的WT1、WT2、WT4迅速减少出力，由图4可知，虽然其转速得以快速恢复，但造成了较大的功率缺额，引起了二次频率跌落，恶化了系统频率表现。

本文策略和CC 策略下的风机一致性因子Ci如附录A 图A2所示。由图可知，本文策略下各风机的一致性因子在调频过程中基本一致，表明本文策略可以实现风机状态一致的控制目标。而如前文所述，由于CC 策略的功率分配方式不合理，各风机在调频过程中的状态不一致，对应的一致性因子变化差别较大，导致WT3、WT5的一致性因子提前归0，即风机提前退出调频，恢复到初始状态的现象，使得风电场出力下降，拉低了频率最低点。

3.1.2 负荷突减场景

设场景2 为母线7 在t=5 s 时发生500 MW 的负荷突减事件。该场景下，不同控制策略下的系统频率、风电场出力结果见图5。由图可以看出，本文策略的频率表现仍最好，其频率最高点为51.37 Hz，相较于CC策略和NoWT策略分别降低了0.25、0.72 Hz。

图5 不同控制策略下的系统频率和风电场出力（场景2）Fig.5 System frequency and wind farm output under different control strategies（Scene 2）

本文策略和CC 策略下的风机出力见附录A 图A3。由图可知，与负荷突增的场景类似，由于CC 策略的功率分配不合理，风电场内初始风速较大（即可向下调频能力较小）的WT1、WT2在频率支撑阶段结束时的转速就达到了限值，触发了风机转速保护，使WT1、WT2提前退出调频，造成CC 策略下风电场频率支撑后半段（8～15.5 s）相比本文策略功率盈余。由于本文采用渐进转速恢复控制策略，风机出力在两阶段切换时无明显变化，因此本文策略下的频率未出现明显的二次跌落现象。而CC 策略采用不合理的转速恢复控制，在15.5 s 时出现了风电场出力突增的情况，在转速恢复阶段开始后，场内未退出的WT3— WT5由于采用阶跃式转速恢复控制策略，其出力迅速升高，转速迅速下降，恢复到事发前的初始值。

不同的负荷突变场景下，采用不同控制策略的系统频率极值见表1。由表可知，采用本文策略向上或向下调频时，相较于CC、NOWT 策略，其在频率表现上均有较明显的提升。结合图4 可知，CC 策略下有风机的转速达到限值，而采用本文策略时，在整个风电场调频过程中风机都处于安全转速范围内。综上可知，不论是在维持系统频率方面还是保障风电场安全性方面，本文策略均比CC策略表现更佳。

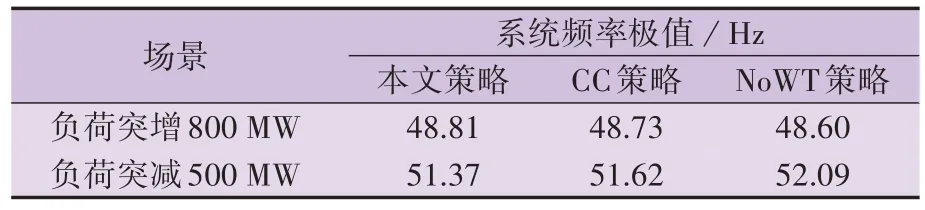
表1 不同负荷突变场景下系统频率极值Table 1 Frequency extreme values of system under different load sudden change scenarios

3.2 含风电场的3端4区直流系统

含风电场的3 端4 区直流系统拓扑见附录A 图A4。其中区域1 含4 台同步机（G1— G4），区域2 含2 台同步机（G5、G6），区域3 为1 座风电场，含有5 台聚合风机（WT1— WT5），风机的转动惯量均为4 s。区域1 的额定频率为50 Hz，额定容量为100 MW。区域3 的风电场通过直流电网与区域1、2 相连。DC1、DC2、DC4处的换流站均采用电压-功率下垂控制，DC3处的换流站采用定电压幅频控制。该系统稳定运行状态下的潮流分布见图A4。为了体现风电场主动参与调频的控制效果，该模型中同步机的时间惯量设置较小，G1、G2、G5、G6的时间惯量均设置为3.5 s，G3、G4的时间惯量均设置为3.175 s。经柔性直流并网的风电场采用的频率控制策略可参考文献［21-22］。

设场景3为母线9在t=10 s时负荷突增900 MW。该场景下，采用不同控制策略时区域1 的系统频率和风电场出力如图6 所示，各风机的转速变化如附录A 图A5 所示。由图6 可知，采用本文策略时的调频效果仍最佳，其系统频率最低点为49.9 Hz，CC 策略的频率最低点为49.87 Hz，而NoWT策略的频率最低点为49.81 Hz。相较于CC 策略、NoWT 策略，本文策略将频率最低点分别提升了0.03、0.09 Hz。

图6 不同控制策略下的系统频率和风电场出力（场景3）Fig.6 System frequency and wind farm output under different control strategies（Scene 3）

一方面，与4 机2 区系统的仿真结果类似，由于CC 策略无法根据各风机的调频能力合理分配频率支撑功率，转速较小的WT1、WT2在频率支撑阶段还未结束时转速就降到最低限值，触发了转速保护，提前退出调频；WT1、WT3的一致性因子在10～15 s时段内迅速降落，导致CC策略下该期间的风电场出力低于本文策略。另一方面，在3 端4 区直流系统算例中，频率支撑阶段与转速恢复阶段切换的时间定在风机提供频率支撑10 s 后，由图A5 可知：由于本文策略采用了渐进转速恢复策略，风机能平滑地过渡到转速恢复阶段，其转速变化以及一致性因子变化均较平缓；而当采用CC 策略时，风机在切换至转速恢复阶段时，一致性因子陡减，引起风电场出力在20 s时迅速下降，进一步造成了二次频率跌落现象。

综上可知，在该3 端4 区直流系统中，本文策略不仅能提升系统的频率最低点，还可以在风电场提供频率调节服务过程中保证各风机的状态一致性，从而保障风电场安全运行。